Алгебра
План урока:
Иррациональные уравнения
Ранее мы рассматривали целые и дробно-рациональные уравнения. В них выражение с переменной НЕ могло находиться под знаком радикала, а также возводиться в дробную степень. Если же переменная оказывается под радикалом, то получается иррациональное уравнение.
Приведем примеры иррациональных ур-ний:
Заметим, что не всякое уравнение, содержащее радикалы, является иррациональным. В качестве примера можно привести
Это не иррациональное, а всего лишь квадратное ур-ние. Дело в том, что под знаком радикала стоит только число 5, а переменных там нет.
Простейшие иррациональные уравнения
Начнем рассматривать способы решения иррациональных уравнений. В простейшем случае в нем справа записано число, а вся левая часть находится под знаком радикала. Выглядит подобное ур-ние так:
где а – некоторое число (константа), f(x) – рациональное выражение.
Для его решения необходимо обе части возвести в степень n, тогда корень исчезнет:
Получаем рациональное ур-ние, решать которые мы уже умеем. Однако есть важное ограничение. Мы помним, что корень четной степени всегда равен положительному числу, и его нельзя извлекать из отрицательного числа. Поэтому, если в ур-нии
n – четное число, то необходимо, чтобы а было положительным. Если же оно отрицательное, то ур-ние не имеет корней. Но на нечетные n такое ограничение не распространяется.
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число (– 6), но квадратный корень (если быть точными, то арифметический квадратный корень) не может быть отрицательным. Поэтому ур-ние корней не имеет.
Ответ: корней нет.
Пример. Решите ур-ние
Решение. Теперь справа стоит положительное число, значит, мы имеем право возвести обе части в квадрат. При этом корень слева исчезнет:
Пример. Решите ур-ние
Решение. Справа стоит отрицательное число, но это не является проблемой, ведь кубический корень может быть отрицательным. Возведем обе части в куб:
Конечно, под знаком корня может стоять и более сложное выражение, чем (х – 5).
Пример. Найдите решение ур-ния
Решение. Возведем обе части в пятую степень:
х 2 – 14х – 32 = 0
Получили квадратное ур-ние, которое можно решить с помощью дискриминанта:
D = b 2 – 4ac = (– 14) 2 – 4•1•(– 32) = 196 + 128 = 324
Итак, нашли два корня: (– 2) и 16.
Несколько более сложным является случай, когда справа стоит не постоянное число, а какое-то выражение с переменной g(x). Алгоритм решения тот же самый – необходимо возвести в степень ур-ние, чтобы избавиться от корня. Но, если степень корня четная, то необходимо проверить, что полученные корни ур-ния не обращают правую часть, то есть g(x), в отрицательное число. В противном случае их надо отбросить как посторонние корни.
Пример. Решите ур-ние
Решение. Возводим обе части во вторую степень:
х – 2 = х 2 – 8х + 16
D = b 2 – 4ac = (– 9) 2 – 4•1•18 = 81 – 72 = 9
Получили два корня, 3 и 6. Теперь проверим, во что они обращают правую часть исходного ур-ния (х – 4):
при х = 3 х – 4 = 3 – 4 = – 1
при х = 6 6 – 4 = 6 – 4 = 2
Корень х = 3 придется отбросить, так как он обратил правую часть в отрицательное число. В результате остается только х = 6.
Пример. Решите ур-ние
Решение. Здесь используется кубический корень, а потому возведем обе части в куб:
3х 2 + 6х – 25 = (1 – х) 3
3х 2 + 6х – 25 = 1 – 3х + 3х 2 – х 3
Получили кубическое ур-ние. Решить его можно методом подбора корня. Из всех делителей свободного коэффициента (– 26) только двойка обращает ур-ние в верное равенство:
Других корней нет. Это следует из того факта, что функция у = х 3 + 9х – 26 является монотонной.
Заметим, что если подставить х = 2 в левую часть исходного ур-ния 1 – х, то получится отрицательное число:
при х = 2 1 – х = 1 – 2 = – 1
Но означает ли это, что число 2 НЕ является корнем? Нет, ведь кубический корень вполне может быть и отрицательным (в отличие от квадратного). На всякий случай убедимся, что двойка – это действительно корень исходного уравнения:
Уравнения с двумя квадратными корнями
Ситуация осложняется, если в ур-нии есть сразу два квадратных корня. В этом случае их приходится убирать последовательно. Сначала мы переносим слагаемые через знак «=» таким образом, чтобы слева остался один из радикалов и ничего, кроме него. Возводя в квадрат такое ур-ние, мы избавимся от одного радикала, после чего мы получим более простое ур-ние. После получения всех корней надо проверить, какие из них являются посторонними. Для этого их надо просто подставить в исходное ур-ние.
Пример. Решите ур-ние
Решение. Перенесем вправо один из корней:
Возведем обе части в квадрат. Обратите внимание, что левый корень при этом исчезнет, а правый – сохранится:
Теперь снова перемещаем слагаемые так, чтобы в одной из частей не осталось ничего, кроме корня:
Снова возведем ур-ние в квадрат, чтобы избавиться и от второго корня:
(2х – 4) 2 = 13 – 3х
4х 2 – 16х + 16 = 13 – 3х
4х 2 – 13х + 3 = 0
D = b 2 – 4ac = (– 13) 2 – 4•4•3 = 169 –48 = 121
Имеем два корня: 3 и 0,25. Но вдруг среди них есть посторонние? Для проверки подставим их в исходное ур-ние. При х = 0,25 имеем:
Получилось ошибочное равенство, а это значит, что 0,25 не является корнем ур-ния. Далее проверим х = 3
На этот раз получилось справедливое равенство. Значит, тройка является корнем ур-ния.
Введение новых переменных
Предложенный метод последовательного исключения радикалов плохо работает в том случае, если корни не квадратные, а имеют другую степень. Рассмотрим ур-ние
Последовательно исключить корни, как в предыдущем примере, здесь не получится (попробуйте это сделать самостоятельно). Однако помочь может замена переменной.
Для начала перепишем ур-ние в более удобной форме, когда вместо корней используются степени:
х 1/2 – 10х 1/4 + 9 = 0
Теперь введем переменную t = x 1/4 . Тогда х 1/2 = (х 1/4 ) 2 = t 2 . Исходное ур-ние примет вид
Это квадратное ур-ние. Найдем его корни:
D = b 2 – 4ac = (– 10) 2 – 4•1•9 = 100 – 36 = 64
Получили два значения t. Произведем обратную замену:
х 1/4 = 1 или х 1/4 = 9
Возведем оба ур-ния в четвертую степень:
(х 1/4 ) 4 = 1 4 или (х 1/4 ) 4 = 3 4
х = 1 или х = 6561
Полученные числа необходимо подставить в исходное ур-ние и убедиться, что они не являются посторонними корнями:
В обоих случаях мы получили верное равенство 0 = 0, а потому оба числа, 1 и 6561, являются корнями ур-ния.
Пример. Решите ур-ние
х 1/3 + 5х 1/6 – 24 = 0
Решение. Произведем замену t = x 1/6 , тогда х 1/3 = (х 1/6 ) 2 = t 2 . Исходное ур-ние примет вид:
Его корни вычислим через дискриминант:
D = b 2 – 4ac = 5 2 – 4•1•(– 24) = 25 + 96 = 121
Далее проводим обратную заменуx 1/6 = t:
х 1/6 = – 8 или х 1/6 = 3
Первое ур-ние решений не имеет, а единственным решением второго ур-ния является х = 3 6 = 729. Если подставить это число в исходное ур-ние, то можно убедиться, что это не посторонний корень.
Замена иррационального уравнения системой
Иногда для избавления от радикалов можно вместо них ввести дополнительные переменные и вместо одного иррационального ур-ния получить сразу несколько целых, которые образуют систему. Это один из самых эффективных методов решения иррациональных уравнений.
Пример. Решите ур-ние
Решение. Заменим первый корень буквой u, а второй – буквой v:
Исходное ур-ние примет вид
Если возвести (1) и (2) в куб и квадрат соответственно (чтобы избавиться от корней), то получим:
Ур-ния (3), (4) и (5) образуют систему с тремя неизвестными, в которой уже нет радикалов:
Попытаемся ее решить. Сначала сложим (4) и (5), ведь это позволит избавиться от переменной х:
(х + 6) + (11 – х) = u 3 + v 2
из (3) можно получить, что v = 5 – u. Подставим это в (6) вместо v:
17 = u 3 + (5 – u) 2
17 = u 3 + u 2 – 10u + 25
u 3 + u 2 – 10u + 8 = 0
Получили кубическое ур-ние. Мы уже умеем решать их, подбирая корни. Не вдаваясь в подробности решения, укажем, что корнями этого ур-ния являются числа
подставим полученные значения в (4):
x + 6 = 1 3 или х + 6 = 2 3 или х + 6 = (– 4) 3
x + 6 = 1 или х + 6 = 8 или х + 6 = – 64
х = – 5 или х = 2 или х = – 70
Итак, нашли три возможных значения х. Но, конечно же, среди них могут оказаться посторонние корни. Поэтому нужна проверка – подставим полученные результаты в исходное ур-ние. При х = – 5 получим
Корень подошел. Проверяем следующее число, х = 2:
Корень снова оказался верным. Осталась последняя проверка, для х = – 70:
Итак, все три числа прошли проверку.
Уравнения с «вложенными» радикалами
Порою в ур-нии под знаком радикала стоит ещё один радикал. В качестве примера приведем такую задачу:
При их решении следует сначала избавиться от «внешнего радикала», после чего можно будет заняться и внутренним. То есть в данном случае надо сначала возвести обе части равенства в квадрат:
Внешний радикал исчез. Теперь будем переносить слагаемые, чтобы в одной из частей остался только радикал:
Хочется поделить полученное ур-ние (1) на х, однако важно помнить, что деление на ноль запрещено. То есть, если мы делим на х, то мы должны наложить дополнительное ограничение х ≠ 0. Случай же, когда х всё же равен нулю, мы рассматриваем отдельно. Для этого подставим х = 0 сразу в исходное ур-ние:
Получили верное рав-во, значит, 0 является корнем. Теперь возвращаемся к (1) и делим его на х:
Возводим в квадрат и получаем:
х 2 + 40 = (х + 4) 2
х 2 + 40 = х 2 + 8х + 16
И снова нелишней будет проверка полученного корня:
Иррациональные неравенства
По аналогии с иррациональными ур-ниями иррациональными неравенствами называют такие нер-ва, в которых выражение с переменной находится под знаком радикала или возводится в дробную степень. Приведем примеры иррациональных нер-в:
Нет смысла решать иррациональные нер-ва, если есть проблемы с более простыми, то есть рациональными нер-вами, а также с их системами. Поэтому на всякий случай ещё раз просмотрите этот и ещё вот этот уроки.
Начнем с решения иррациональных неравенств простейшего вида, у которых в одной из частей стоит выражение под корнем, а в другой – постоянное число. Достаточно очевидно, что нер-во вида
Может быть справедливым только тогда, когда
То есть, грубо говоря, нер-ва можно возводить в степень. Однако при этом могут возникнуть посторонние решения. Дело в том, что нужно учитывать и тот факт, что подкоренное выражение должно быть неотрицательным в том случае, если степень корня является четной. Таким образом, нер-во
при четном n можно заменить системой нер-в
Пример. При каких значениях x справедливо нер-во
Решение. С одной стороны, при возведении нер-ва в квадрат мы получим такое нер-во:
х ⩽ – 5 (знак нер-ва изменился из-за того, что мы поделили его на отрицательное число)
Получили промежуток х∈(– ∞; – 5). Казалось бы, надо записать ещё одно нер-во
чтобы подкоренное выражение было неотрицательным. Однако сравните (1) и (2). Ясно, что если (1) выполняется, то справедливым будет и (2), ведь если какое-то выражение больше или равно двум, то оно автоматически будет и больше нуля! Поэтому (2) можно и не решать.
Теперь посмотрим на простейшие нер-ва с корнем нечетной степени.
Пример. Найдите решение нер-ва
Решение. Всё очень просто – надо всего лишь возвести обе части в куб:
x 2 – 7x– 8 2 – 7x– 8 = 0
D = b 2 – 4ac = (– 7) 2 – 4•1•(– 8) = 49 + 32 = 81
Далее полученные точки отмечаются на координатной прямой. Они разобьют ее на несколько промежутков, на каждом из которых функция у =x 2 – 7x– 8 сохраняет свой знак. Определить же этот самый знак можно по направлению ветвей параболы, которую рисует схематично:
Видно, что парабола располагается ниже оси Ох на промежутке (– 1; 8). Поэтому именно этот промежуток и является ответом. Нер-во строгое, поэтому сами числа (– 1) и 8 НЕ входят в ответ, то есть для записи промежутка используются круглые скобки.
Обратите внимание: так как в исходном нер-ве используется корень нечетной (третьей) степени, то нам НЕ надо требовать, чтобы он был неотрицательным. Он может быть меньше нуля.
Теперь рассмотрим более сложный случай, когда в правой части нер-ва стоит не постоянное число, а некоторое выражение с переменной, то есть оно имеет вид
Случаи, когда n является нечетным числом, значительно более простые. В таких ситуациях достаточно возвести нер-во в нужную степень.
Пример. Решите нер-во
Решение.Слева стоит кубический корень, а возведем нер-во в третью степень (при этом мы используем формулу сокращенного умножения):
И снова квадратное нер-во. Найдем нули функции записанной слева, и отметим их на координатной прямой:
D = b 2 – 4ac = (– 1) 2 – 4•1•(– 2) = 1 + 8 = 9
Нер-во выполняется при х∈(– ∞; – 1)⋃(2; + ∞). Так как мы возводили нер-во в нечетную степень, то больше никаких действий выполнять не надо.
стоит корень четной степени, то ситуация резко осложняется. Его недостаточно просто возвести его в n-ую степень. Необходимо выполнение ещё двух условий:
f(x) > 0 (подкоренное выражение не может быть отрицательным);
g(x) > 0 (ведь сам корень должен быть неотрицательным, поэтому если g(x)будет меньше нуля, то решений не будет).
Вообще говоря, в таких случаях аналитическое решение найти возможно, но это тяжело. Поэтому есть смысл решить нер-во графически – такое решение будет более простым и наглядным.
Пример. Решите нер-во
Решение. Сначала решим его аналитически, без построения графиков. Возведя нер-во в квадрат, мы получим
х 2 – 10х + 21 > 0(1)
Решением этого квадратного нер-ва будет промежуток (– ∞;3)⋃(7; + ∞). Но надо учесть ещё два условия. Во-первых, подкоренное выражение должно быть не меньше нуля:
Во-вторых, выражение 4 – х не может быть отрицательным:
Получили ограничение 2,5 ⩽ х ⩽ 4, то есть х∈[2,5; 4]. С учетом того, что при решении нер-ва(1) мы получили х∈(– ∞;3)⋃(7; + ∞), общее решение иррационального нер-ва будет их пересечением, то есть промежутком [2,5; 3):
Скажем честно, что описанное здесь решение достаточно сложное для понимания большинства школьников, поэтому предложим альтернативное решение, основанное на использовании графиков. Построим отдельно графики левой и правой части нер-ва:
Видно, что график корня находится ниже прямой на промежутке [2,5; 3). Возникает вопрос – точно ли мы построили график? На самом деле с его помощью мы лишь определили, что искомый промежуток находится между двумя точками. В первой график корня касается оси Ох, а во второй точке он пересекается с прямой у = 4 – х. Найти координаты этих точек можно точно, если решить ур-ния. Начнем с первой точки:
Итак, координата х первой точки в точности равна 2,5. Для нахождения второй точки составим другое ур-ние:
Это квадратное ур-ние имеет корни 3 и 7 (убедитесь в этом самостоятельно). Число 7 является посторонним корнем:
Подходит только число 3, значит, вторая точка имеет координату х = 3, а искомый промежуток – это [2,5; 3).
Ещё тяжелее случаи, когда в нер-ве с корнем четной степени стоит знак «>», а не « 1/2 = х – 3
Как решать квадратные уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, которое содержит переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим 5 + 8 = 12. 13 = 12 — противоречие. Значит, х = 5 не является корнем уравнения.
А вот если х = 4, то при подстановке в уравнение мы получим 4 + 8 = 12. 12 = 12 — верное равенство. Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Квадратные уравнения могут иметь два корня, один корень или не иметь корней.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b 2 − 4ac. А вот свойства дискриминанта:
- если D 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Разобраться в теме еще быстрее с помощью опытного преподавателя можно на курсах по математике в онлайн-школе Skysmart.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент отличается от единицы.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x 2 — 2x + 6 = 0
- x 2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x 2 ), а значит уравнение называется приведенным.
- 2x 2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Пример 1. Превратим неприведенное уравнение: 8x 2 + 20x — 9 = 0 — в приведенное.
Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x 2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax 2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято называть неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax 2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
| Для самых любопытных объясняем откуда появились такие названия: | |
|---|---|
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Решение неполных квадратных уравненийКак мы уже знаем, есть три вида неполных квадратных уравнений:
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам. Как решить уравнение ax 2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0. Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0. Пример 1. Решить −6x 2 = 0.
Как решить уравнение ax 2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
Разделим обе части на 8: Ответ: уравнение 8x 2 + 5 = 0 не имеет корней. Как решить уравнение ax 2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение: Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня: Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0 0,5x = 0,125, Ответ: х = 0 и х = 0,25. Как разложить квадратное уравнениеС помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так: Формула разложения квадратного трехчлена Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2). Дискриминант: формула корней квадратного уравненияЧтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так: где D = b 2 − 4ac — дискриминант квадратного уравнения. Эта запись означает: Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться. Алгоритм решения квадратных уравнений по формулам корнейТеперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни. В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней. Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться! Примеры решения квадратных уравненийКак решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике. Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
Ответ: единственный корень 3,5. Пример 2. Решить уравнение 54 — 6x 2 = 0.
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую Ответ: два корня 3 и — 3. Пример 3. Решить уравнение x 2 — х = 0.
Ответ: два корня 0 и 1. Пример 4. Решить уравнение x 2 — 10 = 39.
Ответ: два корня 7 и −7. Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112 Ответ: корней нет. В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся. Формула корней для четных вторых коэффициентовРассмотрим частный случай. Формула решения корней квадратного уравнения Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней: 2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″> Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид: где D1 = n 2 — ac. Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения. Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
Формула ВиетаЕсли в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства: Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам. Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0. Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре: Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит: Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное. Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется: Результат проделанных вычислений в том, что мы убедились в справедливости выражения: Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она: Обратная теорема Виета Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0. Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение. Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
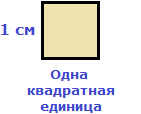
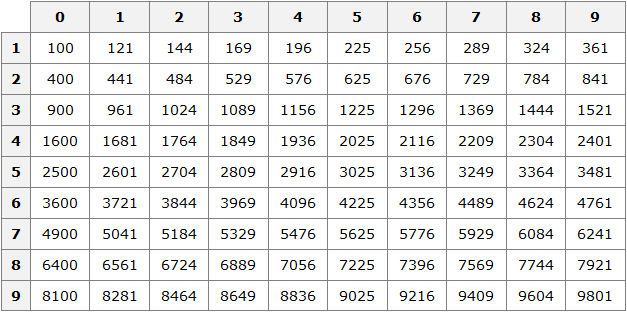
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″> Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы. Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже. Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам: Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p> Упрощаем вид квадратных уравненийЕсли мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту. Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0. Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100. Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов. Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто. А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0. Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0. Связь между корнями и коэффициентамиМы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты: Из этой формулы, можно получить другие зависимости между корнями и коэффициентами. Например, можно применить формулы из теоремы Виета: Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3. Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты: Квадратный кореньОсновные сведенияЧтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень. Найдём площадь квадрата, длина стороны которого 3 см S = 3 2 = 9 см 2 Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени. Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени. Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем. Введём для работы с корнями новые обозначения. Символ кóрня выглядит как Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата) Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня) Получили выражение, которое читается так: « квадратный корень из числа 9» . С этого момента возникает новая задача по поиску самогó корня. Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом: Значит квадрат площадью 9 см 2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня. Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9 Получается, что выражение Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное. Например, извлечём квадратный корень из числа 4 Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4 Поэтому ответ к выражению вида Запишем ответ к выражению ОпределенияДадим определение квадратному корню. Квадратным корнем из числа a называют такое число b, вторая степень которого равна a . То есть число b должно быть таким, чтобы выполнялось равенство b 2 = a . Число b (оно же корень) обозначается через радикал Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16 Корень 4 можно обозначить через радикал Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16 Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным. Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0) , при котором выполняется равенство b 2 = a . В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4. В разговорном языке можно использовать сокращение. К примеру, выражение Не следует путать понятия корень и квадрат . Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно. Корнями же являются числа 5, 6 и 7 . Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно. Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи Квадратный корень из единицы равен единице. То есть справедливо следующее равенство: Это по причине того, что единица во второй степени равна единице: и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице: Квадратный корень из нуля равен нулю. То есть справедливо равенство Выражение вида Если выражение вида Например, выражение Это потому что выражение Корень из квадрата числá равен модулю этого числá: Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5 Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5 , возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5 Действительно, если не пользуясь правилом Не следует путать правило В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так: Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень. Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64. Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7 , а √64 = 8 , Примеры извлечения квадратных корнейРассмотрим несколько простых примеров на извлечение квадратных корней. Пример 1. Извлечь квадратный корень √36 Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 6 2 = 36 Пример 2. Извлечь квадратный корень √49 Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 7 2 = 49 В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть: Но 7 × 7 это 7 2 Пример 3. Извлечь квадратный корень √100 Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10 , поскольку 10 2 = 100 Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов. Пример 3. Извлечь квадратный корень √256 Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов. Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256. Видим, что это число 16 . Значит √256 = 16 . Пример 4. Найти значение выражения 2√16 В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16 , затем перемнóжим его с числом 2 Пример 7. Решить уравнение В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4. Значение переменной x равно 16, поскольку Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же. Из определения мы знаем, что квадратный корень Применим равенство b 2 = a к нашему примеру В выражении 4 2 = x вычислим левую часть, полýчим 16 = x . Поменяем левую и правую часть местами, полýчим x = 16 . В результате приходим к тому, что нашлось значение переменной x . Пример 8. Решить уравнение Перенесем −8 в правую часть, изменив знак: Возведем правую часть во вторую степень и приравняем её к переменной x Вычислим правую часть, полýчим 64 = x . Поменяем левую и правую часть местами, полýчим x = 64 . Значит корень уравнения Пример 9. Решить уравнение Воспользуемся определением квадратного корня: Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x . Возведем число 7 во вторую степень и приравняем его к 3 + 5x В выражении 7 2 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x . Получилось обычное линейное уравнение. Решим его: Корень уравнения Пример 10. Найти значение выражения В этом выражении число 2 умножается на квадратный корень из числа 49. Сначала нужно извлечь квадратный корень и перемножить его с числом 2 Приближённое значение квадратного корняНе каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению. Например, извлечь квадратный корень А извлечь квадратный корень Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению. Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее. Найдём значение корня Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу: Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2 А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства: Точные значения корней √1 и √4 известны. Это числа 1 и 2 Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел. Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1 Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3 , потому что оно малó. Проверим тогда дробь 1,8 Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3 , потому что оно великó. Проверим тогда дробь 1,7 Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3 . Напомним, что знак приближенного значения выглядит как ≈ Значение 1,6 проверять не нужно, потому что в результате получится число 2,56 , которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим. В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых. Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8 Проверим дробь 1,74 Получился результат 3,0276 , который близок к подкореннóму выражению, но превосходит его на 0,0276 . Значит значение 1,74 великó для корня √3 . Проверим тогда дробь 1,73 Получился результат 2,9929 , который близок к подкореннóму выражению √3 . Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых. Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее: √3 = 1,732 (вычислено с точностью до тысячных) √3 = 1,7320 (вычислено с точностью до десятитысячных) √3 = 1,73205 (вычислено с точностью до ста тысячных). Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице: Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его. В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее. Приближенное значение квадратного корня с недостатком или избыткомИногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком. В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89 . Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3. С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24 . Этот результат превосходит подкореннóе выражение на 0,24 . То есть 3,24 − 3 = 0,24 . Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком: Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2. Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2 Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком: Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком. Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых» , заменяют на словосочетания «с точностью до 1» , «с точностью до 0,1» , «с точностью до 0,01» соответственно. Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых: Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1 Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1 Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01 Границы, в пределах которых располагаются корниЕсли исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10]. Например, пусть исходным числом будет 64 . Данное число принадлежит промежутку [1; 100] . Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10] . Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64 ? Ясно, что перемножение 8 × 8 , а это есть 8 2 = 64 . Значит квадратный корень из числа 64 есть 8 Пример 2. Извлечь квадратный корень из числа 49 Число 49 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 7 , поскольку 7 2 = 49 Пример 2. Извлечь квадратный корень из числа 1 Число 1 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 1, поскольку 1 2 = 1 Пример 3. Извлечь квадратный корень из числа 100 Число 100 принадлежит промежутку [1; 100] . Значит квадратный корень будет принадлежать промежутку [1; 10] . Этим корнем будет число 10, поскольку 10 2 = 100 Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10] . Например, извлечём квадратный корень из числа 37 . Нет целого числа, вторая степень которого была бы равна 37 . Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых: Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36 . Квадратный корень из него равен 6 . И далее отталкиваясь от числа 6 , можно находить приближённое значение корня √37 , проверяя различные десятичные дроби, целая часть которых равна 6 . Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты: 1 2 = 1 И обратно, следует знать значения квадратных корней этих квадратов: Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей. Например, 6 2 = 36 . Допишем к числу 6 один ноль, полýчим 60 . Возведём число 60 во вторую степень, полýчим 3600 А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей: Тогда можно сделать следующий вывод: Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа. Например, извлечём квадратный корень из числа 900 . Видим, что в данном числе есть знакомый нам квадрат 9 . Извлекаем из него корень, получаем 3 Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3 Пример 2. Извлечём квадратный корень из числа 90000 Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля: Пример 3. Извлечем квадратный корень из числа 36000000 Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля: Пример 4. Извлечем квадратный корень из числа 2500 Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль: Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно. Например, И наоборот, если в равенстве Пример 2. Увеличим в равенстве Пример 3. Уменьшим в равенстве Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100 . Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз. Например, извлечём квадратный корень из числа 0,25 . В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25. Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко: Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100 . В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру. Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат. Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225 , квадратный корень из которого равен 35 . Тогда можно извлечь квадратный корень и из 0,1225 . Умнóжим данную десятичную дробь на 10000 , полýчим 1225 . Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов: Но нам изначально нужно было извлечь корень из 0,1225 , а не из 1225 . Чтобы исправить ситуацию, в равенстве Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25 . Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби. Умнóжим десятичную дробь 12,25 на 100 , полýчим 1225 . Извлечём корень из числа 1225 Теперь в равенстве Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100]. В этом случае применяется таблица квадратов: Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000] . Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100] . Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576 Видим, что это число 24. Значит Пример 2. Извлечь квадратный корень из числа 432 . Число 432 принадлежит промежутку [100; 10000] . Значит квадратный корень следует искать в промежутке [10; 100] . Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо. Извлечем квадратный корень из числа 432 с точностью до десятых. В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20. Проверим, например, число 20,8. Для этого возведём его в квадрат: Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432 . Проверим тогда значение 20,7 Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49 , которое меньше исходного числа 432 , но близко к нему. Значит √432 ≈ 20,7 . Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце. Например, извлечём корень из числа 4225 . Нам известен ближайший меньший квадрат 3600 , и ближайший больший квадрат 4900 Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно: Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70 . Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900 . Затем можно проверить, например, корень 64 . Возведём его в квадрат (или умнóжим данное число само на себя) Корень 64 не годится. Проверим корень 65 Получается 4225. Значит 65 является корнем числа 4225 Тождественные преобразования с квадратными корнямиНад квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований. Квадратный корень из произведенияКвадратный корень из произведения это выражение вида Например, выражение Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9 , которое равно 36 . Затем извлечь квадратный корень из числа 36 Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным. Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12 Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются. Итак, разлóжим число 144 на простые множители: Получили следующее разложение: В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2. Тогда четыре двойки можно заменить на запись 2 2 × 2 2 , а две тройки заменить на 3 2 В результате будем иметь следующее разложение: Теперь можно извлекáть квадратный корень из разложения числа 144 Применим правило извлечения квадратного корня из произведения: Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения. Тогда получится произведение 2 × 2 × 3 , которое равно 12 Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители. Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3 . Это разложение можно записать под кóрнем как есть: затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки: Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ: С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов. Например, извлечём квадратный корень из числа 13456 . Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители. Итак, разложим число 13456 на простые множители: В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 2 2 . А два числа 29 предстáвим как 29 2 . В результате полýчим следующее разложение числа 13456 Теперь будем извлекать квадратный корень из разложения числа 13456 Итак, если a ≥ 0 и b ≥ 0 , то Докажем равенство Согласно определению, квадратным корня из числа a есть число b , при котором выполняется равенство b 2 = a . В нашем случае нужно удостовериться, что правая часть равенства Итак, выпишем правую часть равенства Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень: Ранее было сказано, что если выражение вида Значит равенство Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
Пример 1. Найти значение квадратного корня Запишем корень Пример 2. Найти значение квадратного корня Предстáвим число 250 в виде произведения чисел 25 и 10 . Делать это будем под знáком корня: Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100 Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ: Пример 3. Найти значение квадратного корня Воспользуемся правилом возведения степени в степень. Степень 11 4 предстáвим как (11 2 ) 2 . Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа: В нашем случае квадратный корень из числа (11 2 ) 2 будет равен 11 2 . Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется: Далее возводим число 11 во вторую степень и получаем окончательный ответ: Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 11 4 нужно записать в виде произведения 11 2 × 11 2 . Затем извлечь квадратный корень из этого произведения: Пример 4. Найти значение квадратного корня Перепишем степень 3 4 в виде (3 2 ) 2 , а степень 5 6 в виде (5 3 ) 2 Далее используем правило извлечения квадратного кóрня из произведения: Далее используем правило извлечения квадратного кóрня из квадрата числа: Вычислим произведение получившихся степеней и полýчим окончательный ответ: Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения Запишем корень Пример 6. Найти значение квадратного корня Пример 7. Найти значение квадратного корня Если первый сомножитель умножить на число n , а второй сомножитель разделить на это число n , то произведение не изменится. Например, произведение 8 × 4 равно 32 Умнóжим сомножитель 8 скажем на число 2 , а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2 , которое тоже равно 32 . Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались. Например, извлечём квадратный корень из произведения Проанализировав подкореннóе выражение 1,6 × 90 , можно заметить, что если первый сомножитель 1,6 умножить на 10 , а второй сомножитель 90 разделить на 10 , то полýчится произведение 16 × 9 . Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения. Запишем полное решение данного примера: Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче: Пример 9. Найти значение квадратного корня Умнóжим первый сомножитель на 10 , а второй раздéлим на 10 . Тогда под кóрнем образуется произведение 36 × 0,04 , квадратный корень из которого извлекается: Если в равенстве Например, узнáем чему равно значение выражения Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом Теперь найдём значение произведения, находящегося под корнем: А квадратный корень из числа 400 извлекается. Он равен 20 Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются. Например, найдём значение выражения Воспользуемся правилом Сомножитель 32 это 2 5 . Предстáвим этот сомножитель как 2 × 2 4 Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 2 4 предстáвим в виде степени с показателем 2 Теперь воспóльзуемся правилом Пример 12. Найти значение выражения Воспользуемся правилом Сомножитель 8 это 2 × 2 × 2 , а сомножитель 98 это 2 × 7 × 7 Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 2 2 × 2 2 , а две семёрки как 7 2 Теперь воспользуемся правилом Квадратный корень из дробиКвадратный корень вида Например, квадратный корень из дроби Вычислим квадратные корни в числителе и знаменателе: Значит, квадратный корень из дроби Докáжем, что равенство Возведём правую часть во вторую степень. Если в результате полýчим дробь Пример 1. Извлечь квадратный корень Воспользуемся правилом извлечения квадратного корня из дроби: Пример 2. Извлечь квадратный корень Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби: Пример 3. Извлечь квадратный корень Квадратным корнем из числа 0,09 является 0,3 . Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби. Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых: Теперь можно воспользоваться правилом извлечения квадратного корня из дроби: Пример 4. Найти значение выражения Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты: Также можно воспользоваться правилом извлечения квадратного корня из дроби: В данном примере первый способ оказался проще и удобнее. Пример 5. Найти значение выражения Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4 Пример 6. Найти значение выражения Сначала найдём значение квадратного корня Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение: Вынесение множителя из-под знака корняВ некоторых задачах может быть полезным вынесение множителя из-под знака корня. Рассмотрим квадратный корень из произведения В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение Это и есть вынесение множителя из-под знака корня. На практике подкореннóе выражение чаще всего требуется разложить на множители. Пример 2. Вынести множитель из-под знака корня в выражении Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим: Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем: Пример 3. Вынести множитель из-под знака корня в выражении Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим: Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем: Пример 4. Вынести множитель из-под знака корня в выражении Воспользуемся правилом извлечения квадратного корня из произведения: Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений: Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √ 15 и 11 местами: Пример 5. Вынести множитель из-под знака корня в выражении Разлóжим подкореннóе выражение на множители 4 и 3 Воспользуемся правилом извлечения квадратного корня из произведения: Извлечём корень из числа 4, а выражение √3 остáвим без изменений: Пример 6. Упростить выражение Предстáвим второе слагаемое Теперь в выражениях Во втором слагаемом Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки: Вычислим содержимое скобок, полýчим −1 Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3 Внесение множителя под знак корняРассмотрим следующее выражение: В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения. Сначала извлечём квадратный корень, затем перемнóжим его с числом 5. Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15 Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15. Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень: Итак, если данó выражение Пример 1. Внести множитель под знак корня в выражении Возведём число 7 во вторую степень и внесём его под знак корня: Пример 2. Внести множитель под знак корня в выражении Возведём число 10 во вторую степень и внесем его под знак корня: Пример 3. Внести множитель под знак корня в выражении Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня. Пример 4. Внести множитель по знак корня в выражении В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня: Пример 5. Выполнить возведéние в степень в следующем выражении: Воспользуемся формулой квадрата суммы двух выражений: Роль переменной a в данном случае играет выражение √3 , роль переменной b — выражение √2 . Тогда полýчим: Теперь необходимо упростить получившееся выражение. Для выражений А в выражении Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом источники: http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya http://spacemath.xyz/kvadratnyj-koren/ |








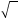 . Это по причине того, что слово корень в математике употребляется как радикал . А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня
. Это по причине того, что слово корень в математике употребляется как радикал . А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня 
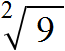
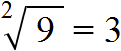
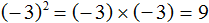
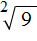 имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.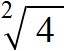
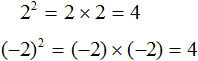
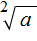 записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.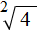 с плюсом и минусом:
с плюсом и минусом: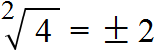
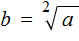 . На практике левая и правая часть поменяны местами и мы видим привычное выражение
. На практике левая и правая часть поменяны местами и мы видим привычное выражение 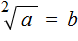
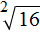 так, что
так, что  .
.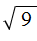 . Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.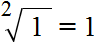
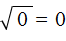 , поскольку 0 2 = 0 .
, поскольку 0 2 = 0 .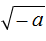 смысла не имеет. Например, не имеет смысла выражение
смысла не имеет. Например, не имеет смысла выражение 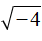 , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
, поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.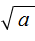 возвести во вторую степень, то есть если записать
возвести во вторую степень, то есть если записать 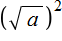 , то это выражение будет равно подкореннóму выражению a
, то это выражение будет равно подкореннóму выражению a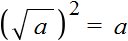
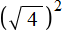 равно 4
равно 4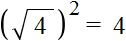
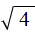 равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.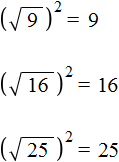
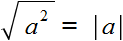
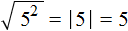
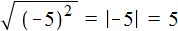
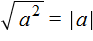 , вычислять выражение
, вычислять выражение 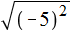 обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5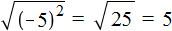
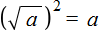 . Правило
. Правило 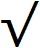
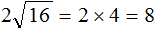
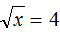
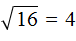 . Значит корень уравнения равен 16.
. Значит корень уравнения равен 16.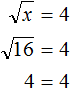
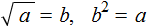
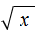 , а именно переменная x
, а именно переменная x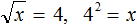
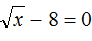
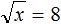
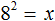
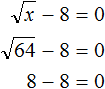
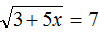
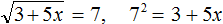
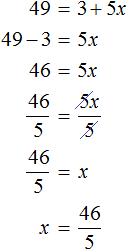
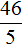 . Выполним проверку, подставив его в исходное уравнение:
. Выполним проверку, подставив его в исходное уравнение: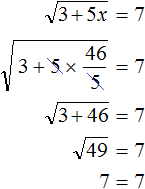
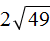
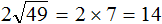
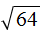 можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8 , поскольку 8 2 = 64 . То есть
можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8 , поскольку 8 2 = 64 . То есть 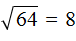
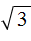 нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
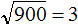
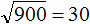
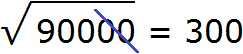
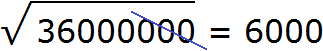
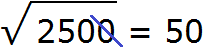
 . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
. Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз: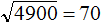
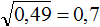
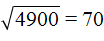 подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз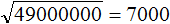
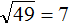
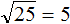
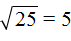 подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз: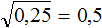
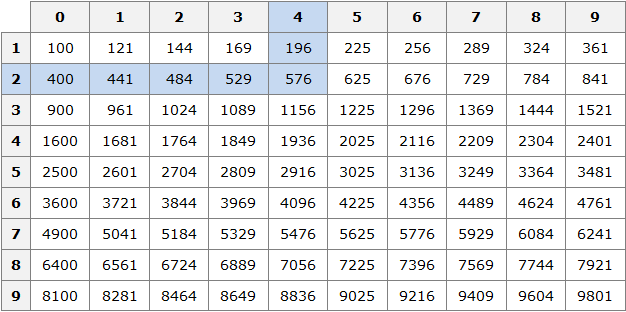
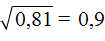 .
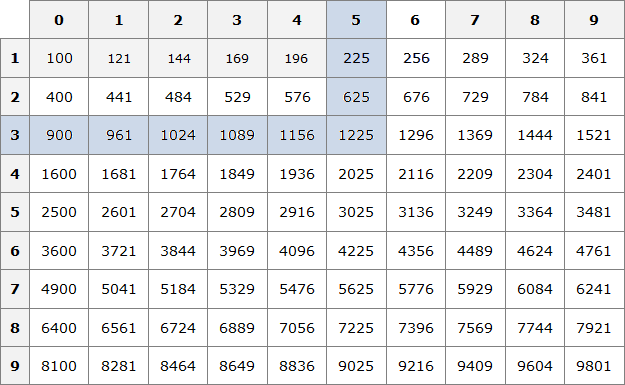
.
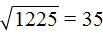
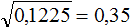
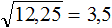
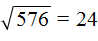 .
.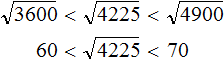
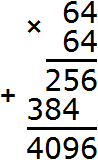
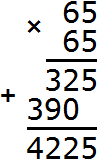
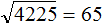
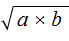 , где a и b некоторые числа.
, где a и b некоторые числа.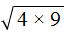 является квадратным корнем из произведения чисел 4 и 9.
является квадратным корнем из произведения чисел 4 и 9.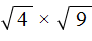 . Вычислив по отдельности эти корни полýчим произведение 2 × 3 , которое равно 6
. Вычислив по отдельности эти корни полýчим произведение 2 × 3 , которое равно 6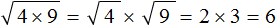
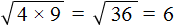

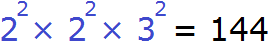
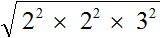
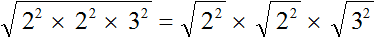
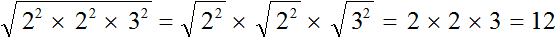
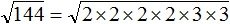
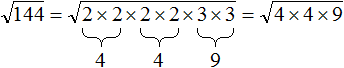
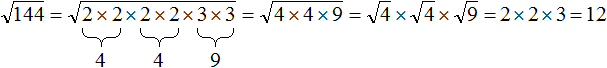

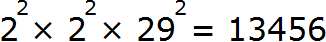
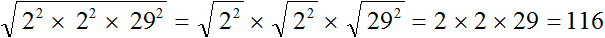
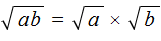 . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
. То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.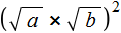
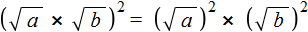
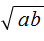
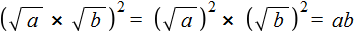
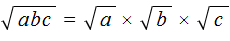 , при a ≥ 0 и b ≥ 0, c ≥ 0.
, при a ≥ 0 и b ≥ 0, c ≥ 0.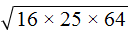
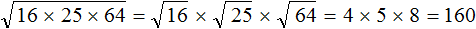
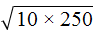
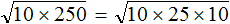
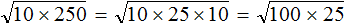
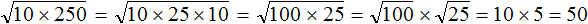
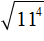
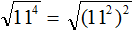
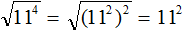
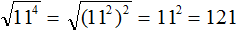
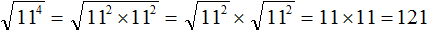
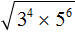
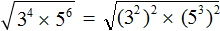
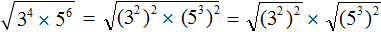
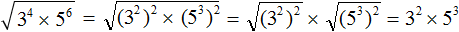
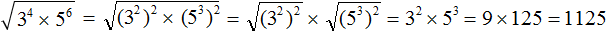
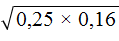
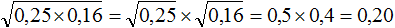
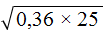
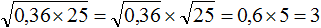
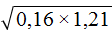
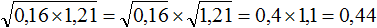
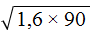 . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.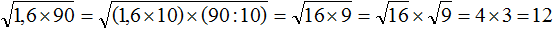
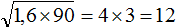
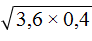
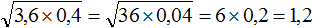
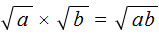 . Это преобразовáние позволяет упрощáть вычисление некоторых корней.
. Это преобразовáние позволяет упрощáть вычисление некоторых корней.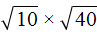 .
.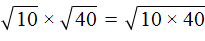
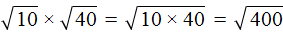

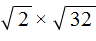 .
.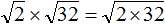
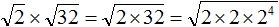
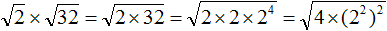
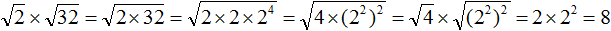
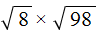
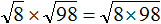
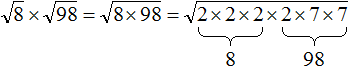
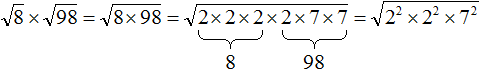
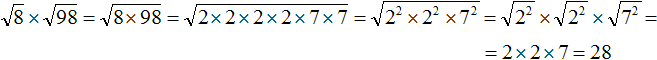
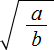 равен дроби, в числителе которой квадратный корень из числа a , а в знаменателе — квадратный корень из числа b
равен дроби, в числителе которой квадратный корень из числа a , а в знаменателе — квадратный корень из числа b
 равен дроби, в числителе которой квадратный корень из числа 4 , а в знаменателе — квадратный корень из числа 9
равен дроби, в числителе которой квадратный корень из числа 4 , а в знаменателе — квадратный корень из числа 9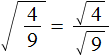
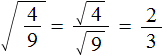
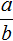 , то это будет означать, что равенство
, то это будет означать, что равенство 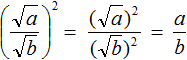
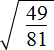
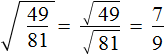
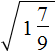
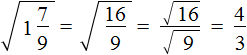
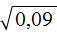
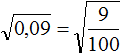
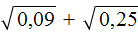
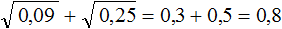
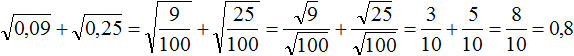
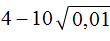
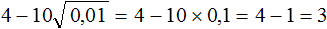
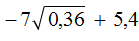
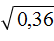 . Он равен 0,6 поскольку 0,6 2 = 0,36
. Он равен 0,6 поскольку 0,6 2 = 0,36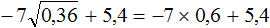
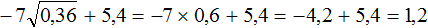
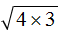 . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
. Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения: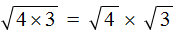
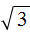 оставим без изменений:
оставим без изменений: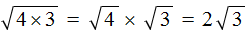
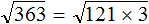
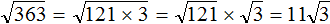
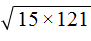
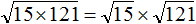
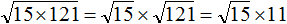
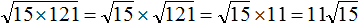
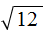
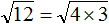
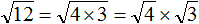
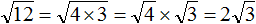
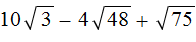
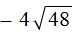 в виде
в виде 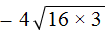 . А третье слагаемое
. А третье слагаемое 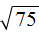 предстáвим в виде
предстáвим в виде 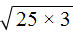
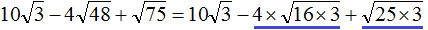
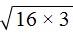 и
и 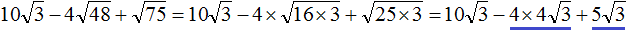
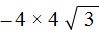 перемнóжим числа −4 и 4 . Остальное перепишем без изменений:
перемнóжим числа −4 и 4 . Остальное перепишем без изменений: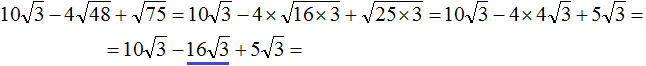
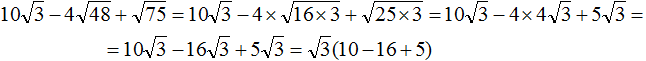
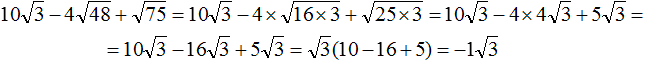
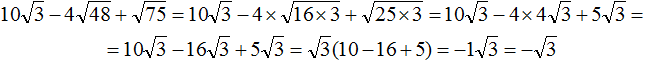
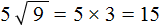

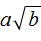 , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
, и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень: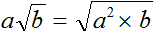
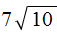
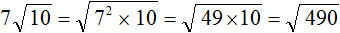
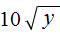
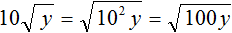
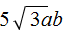
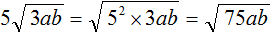
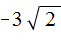
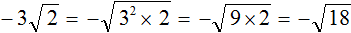
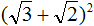
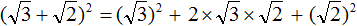
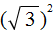 и
и 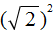 применим правило
применим правило 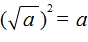 . Ранее мы говорили, что если выражение вида
. Ранее мы говорили, что если выражение вида 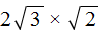 для множителей
для множителей 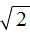 применим правило
применим правило 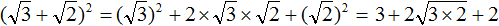
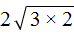 вычислить произведение, которое под кóрнем:
вычислить произведение, которое под кóрнем: