Интегрирование по частям
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Применение метода интегрирования по частям
Типовые разложения по частям
| Вид интеграла | Разложения на части |
| ∫ Pn(x)cos(ax)dx , ∫ Pn(x)sin(ax)dx , ∫ Pn(x)e ax dx , где Pn(x) — некоторый полином (многочлен) степени n | U(x)=Pn(x) , dV(x)=cos(ax)dx |
| ∫ ln(P(x))dx | U=ln(P(x)) ; dV=dx |
| ∫ arcsin(ax)dx | U=arcsin(ax) ; dV=dx |
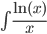 | U=ln(x) ; dV=dx/x |
Интегралы ∫ e ax cos(bx)dx и ∫ e ax sin(bx)dx называются циклическими и вычисляются с использованием формулы интегрирования по частям два раза.
Пример №1 . Вычислить ∫ xe x dx .
Положим U=x , dV=e x dx . Тогда dU=dx , V=e x . Поэтому ∫ xe x dx=xe x — ∫ e x dx=xe x -e x +C .
Пример №2 . Вычислить ∫ xcos(x)dx .
Полагаем U=x , dV=cos(x)dx . Тогда dU=dx , V=sin(x) и ∫ xcos(x)dx=xsin(x) — ∫ sin(x)dx = xsin(x)+cos(x)+C
Пример №3 . ∫ (3x+4)cos(x)dx
Решение:
Интегрирование по частям
Метод интегрирования по частям используется тогда, когда нужно упростить имеющийся неопределенный интеграл или свести его к табличному значению. Чаще всего он применяется в случае наличия показательных, логарифмических, прямых и обратных тригонометрических формул и их сочетаний в подынтегральном выражении.
Основная формула, необходимая для использования этого метода, выглядит так:
∫ f ( x ) d x = ∫ u ( x ) d ( v ( x ) ) = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) )
Она означает, что нам нужно сначала представить выражение под интегралом в качестве произведения функции u ( x ) и дифференциала функции v ( x ) . После этого мы вычисляем значение функции v ( x ) каким-либо методом (чаще всего применяется метод непосредственного интегрирования), а полученные выражения подставляем в указанную формулу, сводя исходный интеграл к разности u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) . Полученный в итоге интеграл также можно взять, используя любой метод интегрирования.
Рассмотрим задачу, в которой нужно найти множество первообразных функции логарифма.
Вычислите неопределенный интеграл ∫ ln ( x ) d x .
Решение
Используем метод интегрирования по частям. Для этого берем ln ( x ) как функцию u ( x ) , а остаток подынтегрального выражения – как d ( v ( x ) ) . В итоге получаем, что ln ( x ) d x = u ( x ) d ( v ( x ) ) , где u ( x ) = ln ( x ) , d ( v ( x ) ) = d x .
Дифференциалом функции u ( x ) является d ( u ( x ) ) — u ‘ ( x ) d x = d x x , а функция v ( x ) может быть представлена как v ( x ) = ∫ d ( v ( x ) ) = ∫ d x = x
Важно: константа C при вычислении функции v ( x ) будет считаться равной 0 .
Подставим то, что у нас получилось, в формулу интегрирования по частям:
∫ ln ( x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = ln ( x ) · x — ∫ x · d x x = ln ( x ) · x — ∫ d x = ln ( x ) · x — x + C 1 = = x ( ln ( x ) — 1 ) + C
Ответ: ∫ ln ( x ) d x = x ( ln ( x ) — 1 ) + C .
Наиболее сложным в применении данного метода является выбор, какую именно часть исходного выражения под интегралом взять в качестве u ( x ) , а какую – d ( v ( x ) ) .
Разберем несколько стандартных случаев.
Если у нас в условии стоят интегралы вида ∫ P n ( x ) · e a x d x , ∫ P n ( x ) · sin ( a x ) d x либо ∫ P n ( x ) · cos ( a x ) d x , где a является коэффициентом, а P n ( x ) – многочленом степени n , то в качестве функции u ( x ) нужно взять именно P n ( x ) .
Найдите множество первообразных функции f ( x ) = ( x + 1 ) · sin ( 2 x ) .
Решение
Мы можем взять по частям неопределенный интеграл ∫ ( x + 1 ) · sin ( 2 x ) d x . Берем x + 1 в качестве u ( x ) и sin ( 2 x ) d x в качестве d ( v ( x ) ) , то есть d ( u ( x ) ) = d ( x + 1 ) = d x .
Используя непосредственное интегрирование, получим:
v ( x ) = ∫ sin ( 2 x ) d x = — 1 2 cos ( 2 x )
Подставляем в формулу интегрирования по частям:
∫ ( x + 1 ) · sin ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = ( x + 1 ) · — 1 2 cos ( 2 x ) — ∫ — 1 2 cos ( 2 x ) d x = = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 2 ∫ cos ( 2 x ) · d ( x ) = = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 4 sin ( 2 x ) + C
Ответ: ∫ ( x + 1 ) · sin ( 2 x ) d x = — 1 2 ( x + 1 ) · cos ( 2 x ) + 1 4 sin ( 2 x ) + C .
Вычислите неопределенный интеграл ∫ ( x 2 + 2 x ) e x d x .
Решение
Берем многочлен второго порядка x 2 + 2 x в качестве u ( x ) и d ( v ( x ) ) — e x d x .
∫ x 2 + 2 x e x d x = u ( x ) = x 2 + 2 x , d ( v ( x ) ) = e x d x d ( u ( x ) ) = ( 2 x + 2 ) d x , v ( x ) = ∫ e x d x = e x = = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = ( x 2 + 2 x ) e x — ∫ ( 2 x + 2 ) e x d x
К тому, что у нас получилось, надо опять применить метод интегрирования по частям:
∫ ( 2 x + 2 ) e x d x = ( x 2 + 2 x ) e x — ∫ 2 x + 2 e x d x = = u ( x ) = ( 2 x + 2 ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = 2 d x , v ( x ) = ∫ e x d x = e x = = ( x 2 + 2 x ) e x — ( 2 x + 2 ) e x — ∫ v ( x ) d ( u ( x ) ) = = ( x 2 + 2 x ) e x — ( 2 x + 2 ) e x — ∫ 2 e x d x = = ( x 2 + 2 x — 2 x — 2 ) e x + 2 ∫ e x d x = ( x 2 — 2 ) e x + 2 e x + C = x 2 e x + C
Ответ: ∫ ( x 2 + 2 x ) e x d x = x 2 e x + C .
Вычислите интеграл ∫ x 3 cos 1 3 x d x .
Решение
Согласно методу интегрирования по частям, берем u ( x ) = x 3 и d ( v ( x ) ) = cos 1 3 x d x .
В таком случае d ( u ( x ) ) = 3 x 2 d x и v ( x ) = ∫ cos 1 3 x d x = 3 sin 1 3 x .
Теперь подставим полученные выражения в формулу:
∫ x 3 cos 1 3 x d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ) ) = = x 3 3 sin 1 3 x — ∫ 3 x 2 3 sin 1 3 x d x = = 3 x 3 sin 1 3 x — 9 ∫ x 2 sin 1 3 x d x
У нас получился неопределенный интеграл, который опять же нужно взять по частям:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x — 9 ∫ x 2 sin 1 3 x d x = = u ( x ) = x 2 , d ( v ( x ) ) = sin 1 3 x d x d ( u ( x ) ) = 2 x d x , v ( x ) = ∫ sin 1 3 x d x = — 3 cos 1 3 x = = 3 x 3 sin 1 3 x — 9 — 3 x 2 cos 1 3 x — ∫ — 3 cos 1 3 x · 2 x d x = = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x — 54 ∫ x cos 1 3 x d x
Выполняем частичное интегрирование еще раз:
∫ x 3 cos 1 3 x d x = 3 x 3 sin 1 3 x + 27 x 2 · cos 1 3 x — 54 ∫ x cos 1 3 x d x = = u ( x ) = x , d ( v ( x ) ) = cos 1 3 x d x d ( u ( x ) ) = d x , v ( x ) = ∫ cos 1 3 x d x = 3 sin 1 3 x = = 3 x 3 sin 1 3 x + 27 x 2 cos 1 3 x — 54 3 x sin 1 3 x — ∫ 3 sin 1 3 x d x = = 3 x 3 — 162 x sin 1 3 x + 27 x 2 cos 1 3 x + 162 ∫ sin 1 3 x d x = = ( 3 x 3 — 162 x ) sin 1 3 x + 27 x 2 cos 1 3 x — 486 cos 1 3 x + C = = ( 3 x 3 — 162 x ) sin 1 3 x + ( 27 x 2 — 486 ) cos 1 3 x + C
Ответ: ∫ x 3 cos 1 3 x d x = ( 3 x 3 — 162 x ) sin 1 3 x + ( 27 x 2 — 486 ) cos 1 3 x + C .
Если же у нас в условии стоят интегралы вида ∫ P n ( x ) · ln ( a x ) d x , ∫ P n ( x ) · a r c sin ( a x ) d x , ∫ P n ( x ) · a r c cos ( a x ) d x , ∫ P n ( x ) · a r c t g ( a x ) d x , ∫ P n ( x ) · a r c c t g ( a x ) d x
то нам следует брать в качестве u ( x ) функции a r c t g ( a x ) , a r c c t g ( x ) , ln ( a x ) , a r c sin ( a x ) , a r cos ( a x ) .
Вычислите множество первообразных функции ( x + 1 ) ln ( 2 x ) .
Решение
Принимаем ln ( 2 x ) в качестве u ( x ) , а ( x + 1 ) d x – в качестве d ( v ( x ) ) . Получаем:
d ( u ( x ) ) = ( ln ( 2 x ) ) ‘ d x = 1 2 x ( 2 x ) ‘ d x = d x x v ( x ) = ∫ ( x + 1 ) d x = x 2 2 + x
Подставим эти выражения в формулу:
∫ ( x + 1 ) ln ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x 2 2 + x ln 2 x — ∫ x 2 2 + x d x x = = x 2 2 + x ln ( 2 x ) — ∫ x 2 + 1 d x = x 2 2 + x ln 2 x — 1 2 ∫ x d x — ∫ d x = = x 2 2 + x ln ( 2 x ) — x 2 4 — x + C
Ответ: ∫ ( x + 1 ) ln ( 2 x ) d x = x 2 2 + x ln ( 2 x ) — x 2 4 — x + C .
Вычислите неопределенный интеграл ∫ x · a r c sin ( 2 x ) d x .
Решение
Решаем, какую часть взять за u ( x ) , а какую – за d ( v ( x ) ) . Согласно правилу, приведенному выше, в качестве первой функции нужно взять a r c sin ( 2 x ) , а d ( v ( x ) ) = x d x . Получим:
d ( u ( x ) ) = ( a r c sin ( 2 x ) ‘ d x = 2 x ‘ d x 1 — ( 2 x ) 2 = 2 d x 1 — ( 2 x ) 2 , v ( x ) = ∫ x d x = x 2 2
Подставляем значения в формулу:
∫ x · a r c sin ( 2 x ) d x = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = = x 2 2 a r c sin ( 2 x ) — ∫ x 2 2 — 2 d x 1 — ( 2 x ) 2 = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2
В итоге мы пришли к следующему равенству:
∫ x · a r c sin ( 2 x ) d x = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2
Теперь вычислим получившийся в итоге интеграл ∫ x 2 d x 1 — 4 x 2 :
∫ x 2 d x 1 — 4 x 2 = ∫ x 2 d x 4 1 4 — x 2 = 1 2 ∫ x 2 d x 1 4 — x 2 = — 1 2 ∫ — x 2 d x 1 4 — x 2 = = — 1 2 ∫ 1 4 — x 2 — 1 4 1 4 — x 2 d x = — 1 2 1 4 — x 2 d x + 1 8 ∫ d x 1 4 — x 2 = = — 1 2 ∫ 1 4 — x 2 d x + 1 8 a r c sin ( 2 x )
Здесь можно применить метод интегрирования по частям и получить:
∫ x 2 d x 1 — 4 x 2 = — 1 2 ∫ 1 4 — x 2 d x + 1 8 a r c sin ( 2 x ) = = u ( x ) = 1 4 — x 2 , d ( v ( x ) ) = d x d ( u ( x ) ) = 1 4 — x 2 ‘ d x 2 1 4 — x 2 = — x d x 1 4 — x 2 , v ( x ) = ∫ d x = x = = — 1 2 u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — ∫ — x 2 d x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — 1 2 ∫ x 2 d x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) = = — 1 2 x 1 4 — x 2 — ∫ x 2 d x 1 — 4 x 2 + 1 8 a r c sin ( 2 x )
Теперь наше равенство выглядит так:
∫ x 2 d x 1 — 4 x 2 = — 1 2 x 1 4 — x 2 — ∫ x 2 d x 1 — 4 x 2 + 1 8 a r c sin ( 2 x )
Мы видим, что интеграл справа аналогичен тому, что получился слева. Переносим его в другую часть и получаем:
2 ∫ x 2 d x 1 — 4 x 2 = — 1 2 x 1 4 — x 2 + 1 8 a r c sin ( 2 x ) + C 1 ⇒ x 2 d x 1 — 4 x 2 = — 1 4 x 1 4 — x 2 + 1 16 a r c sin ( 2 x ) + C 2 x 2 d x 1 — 4 x 2 = — 1 8 x 1 4 — x 2 + 1 16 a r c sin ( 2 x ) + C 2
Вернемся к исходным переменным:
∫ x · a r c sin ( 2 x ) d x = x 2 2 a r c sin ( 2 x ) — ∫ x 2 d x 1 — 4 x 2 = = x 2 2 a r c sin ( 2 x ) — — 1 8 x 1 — 4 x 2 + 1 16 a r c sin ( 2 x ) + C 2 = = 1 2 x 2 — 1 8 a r c sin ( 2 x ) + 1 8 x 1 — 4 x 2 + C
Ответ: ∫ x · a r c sin ( 2 x ) d x = 1 2 x 2 — 1 8 a r c sin ( 2 x ) + 1 8 x 1 — 4 x 2 + C .
Если же у нас в задаче стоит интеграл вида ∫ e a · x · sin ( b x ) d x либо ∫ e a · x · cos ( b x ) d x , то в качестве u ( x ) может быть выбрана любая функция.
Вычислите неопределенный интеграл ∫ e x · sin ( 2 x ) d x .
Решение
∫ e x sin ( 2 x ) d x = u ( x ) = sin ( 2 x ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = 2 cos ( 2 x ) d x , v ( x ) = ∫ e x d x = e x = = u ( x ) v ( x ) — ∫ v ( x ) d ( u ( x ) ) = sin ( 2 x ) e x — ∫ e x · 2 cos 2 x d x = = sin ( 2 x ) e x — 2 ∫ e x cos ( 2 x ) d x = u ( x ) = cos ( 2 x ) , d ( v ( x ) ) = e x d x d ( u ( x ) ) = — 2 sin ( 2 x ) d x , v ( x ) = ∫ e x d x = e x = = sin ( 2 x ) e x — 2 cos ( 2 x ) e x — ∫ ( e x ( — 2 sin ( 2 x ) d x ) ) = = sin ( 2 x ) e x = 2 cos ( 2 x ) e x — 4 ∫ e x sin ( 2 x ) d x
В итоге у нас получится:
∫ e x sin ( 2 x ) d x = sin ( 2 x ) e x — 2 cos ( 2 x ) e x — 4 ∫ e x sin ( 2 x ) d x
Мы видим одинаковые интегралы слева и справа, значит, можем привести подобные слагаемые:
5 ∫ e x sin ( 2 x ) d x = sin ( 2 x ) e x — 2 cos ( 2 x ) e x ⇒ ∫ e x sin ( 2 x ) d x = 1 5 sin ( 2 x ) e x — 2 5 cos ( 2 x ) e x + C
Ответ: ∫ e x sin ( 2 x ) d x = 1 5 sin ( 2 x ) e x — 2 5 cos ( 2 x ) e x + C
Этот способ решения является стандартным, и справа нередко получается интеграл, который идентичен исходному.
Мы рассмотрели наиболее типовые задачи, в которых можно точно определить, какую часть выражения взять за d ( v ( x ) ) , а какую за u ( x ) . В остальных случаях это приходится определять самостоятельно.
Также советуем вам ознакомиться с материалом, посвященным основным методам интегрирования.
Метод интегрирования по частям: объяснение, решение примеров
Суть метода интегрирования по частям
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием — функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального выражения, которая легко интегрируется.
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1) 
2) 


3) 



Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале урока формулу интегрирования по частям

получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.
Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
то её можно записать в виде

который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Есть у метода интегрирования по частям совершенно особенное применение: с его помощью можно выводить рекуррентные формулы для нахождения первообразных функций, когда требуется понизить степень функций под знаком интеграла. Понижение степени необходимо, когда не существует табличных интегралов для таких, например, функций, как синусы и косинусы в степени более второй и их произведения. Рекуррентная формула — это формула для нахождения очередного члена последовательности через предыдущий член. Для обозначенных случаев цель достигается последовательным понижением степени. Так, если подынтегральная функция — синус в четвёртой степени от икса, то методом интегрирования по частям можно найти формулу для интеграла синуса в третьей степени и так далее. Описанной задаче посвящен последний параграф этого урока.
Применяем интегрирование по частям вместе
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:

Решение. В подынтегральном выражении — логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что 

Тогда 

Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к табличному интегралу (8)):
И снова логарифм.
Пример 2. Найти неопределённый интеграл:

Решение. Пусть 

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим, пользуясь производной 6 в таблице производных сложных функций: 

Применяя формулу интегрирования по частям, получаем:
Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) — функцию, не содержащую логарифма, сводящуюся к табличному интегралу 9).
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть 

Тогда, пользуясь табличной производной 12, получаем 

Применяя формулу интегрирования по частям, получаем:
Возвращаясь к переменной x, получаем

Находим изначальный интеграл:

Пример 4. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 5. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Пусть 



Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть 

Тогда 

По формуле интегрирования по частям находим:
Применить интегрирование по частям самостоятельно, а затем посмотреть решение
Пример 7. Найти неопределённый интеграл методом интегрирования по частям:

Пример 8. Найти неопределённый интеграл методом интегрирования по частям:

Пример 9. Найти неопределённый интеграл методом интегрирования по частям:

Снова применяем интегрирование по частям вместе
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем 

Тогда 

По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем 

Тогда 

Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Среди интегралов, которые можно решить методом интегрирования по частям, есть и такие, которые не входят ни в одну из трёх упомянутых в теоретической части групп, относительно которых из практики известно, что лучше обозначать через u, а что через dv. Поэтому в этих случаях нужно пользоваться соображением удобства, также приведённым в параграфе «Суть метода интегрирования по частям»: за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv — такую часть подынтегрального выражения, которая легко интегрируется. Последний пример этого урока — решение именно такого интеграла.
Пример 11. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем 

Тогда 

По формуле интегрирования по частям получаем:
Интегрирование по частям для вывода рекуррентных формул
Случаев, когда требуется понижения степени подынтегральной функции, мы уже коснулись во вводной части урока. Теперь — практика использования для этой цели метода интегрирования по частям.
Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу для

Решение. Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали бы и синус, и косинус. Используя тригонометрические тождества, получаем
Ко второму слагаемому — интегралу — применяем метод интегрирования по частям. Для этого обозначим
Тогда
Находим это второе слагаемое — интеграл:
Теперь находим рекуррентную формулу для исходного интеграла:
С помощью полученной формулы найдём I 4 :
http://zaochnik.com/spravochnik/matematika/integraly-integrirovanie/integrirovanie-po-chastjam/
http://function-x.ru/integral102.html
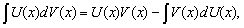
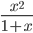 ≡ x^2/(x+2)
≡ x^2/(x+2) 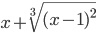 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)





















