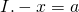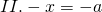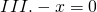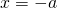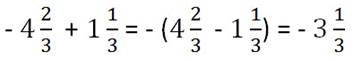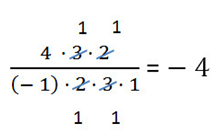Урок математики в 6-м классе «Действия с положительными и отрицательными числами»
Разделы: Математика
Цели:
- повторить, закрепить, обобщить и систематизировать знания детей по теме;
- развивать аналитическое мышление, воображение, память, речь учащихся;
- воспитывать интерес к предмету, чувство гордости и любовь к своей малой Родине, родному краю.
– Добрый день! Здравствуйте, ребята! Тема нашего урока «Действия с положительными и отрицательными числи». А цель вы мне поможете сформулировать позднее. Вначале проверим выполнение домашнего задания. (Домашнее задание к уроку было предложено на карточках. Приложение 2). Каждый ряд в ответе получает одно слово.
1 ряд
2 ряд
3 ряд
Завтра
контрольная
работа
– Ребята, если завтра контрольная работа, то, как вы думаете, какова же цель нашего сегодняшнего урока? (Ответы детей) На протяжении последних уроков математики, мы, учились выполнять действия с положительными и отрицательными числами.
Цель урока – повторить, закрепить, обобщить и систематизировать ваши знания по выполнению действий с положительными и отрицательными числами, полученные на предыдущих уроках; подготовиться к контрольной работе. Девизом нашего урока мне хочется взять слова великого французского философа, физика и математика Рене Декарта: «Мало иметь хороший ум, главное – хорошо его применять». И мы сегодня с вами, ребята, постараемся подтвердить эти слова.
За выполнение каждого задания, во время работы, вы в таблицу будете ставить себе определённое количество баллов.
1. Устный счёт (5 баллов)
Слайды 5-8
– Ребята, у вас на столах лежат карточки с точками (Приложение 3). Ваша задача, решить примеры и выделить те точки, которые соответствуют вашим ответам. Работаем в парах.
– А теперь, выделенные точки, плавно соедините линией. Что же у вас получилось?
Количество баллов за каждое задание проставляйте в таблице итогов (Приложение 4).
Все точки на «5» – 5б., 10 точек – 4б., 8 точек – 3б., 6 точек – 2б., 4 точки – 1б., менее – 0б.
| – (– 4) + (– 3) = 1 – 6 – (– 4) = – 2 5 – (– 8) = 13 – 10 – (– 10) = 0 | 2 • (– 3) = – 6 – 5,3 : 1 = – 5,3 – 3,3 + (– 2,1) = – 5.4 – 22 : 20 = – 1,1 | 0,7 • (– 2) = – 1,4 – 9,4 : 2 = – 4,7 – 4,9 + (– 1,4) = – 6,3 0 + (– 5,8) = – 5 |
2. Найди и исправь ошибки в вычислениях (6 баллов).
| 17 + (– 8) = 25 20 – (– 12) = – 8 – 25 • (– 0,1) = 250 – 42 : (– 0,3) = 140 – 38 + (– 17) = – 21 – 16 – (– 9) = – 7 | 9 32 2,5 правильно – 55 правильно |
Проверку каждого примера сопроводить правилом.
3. Работа над правилами (4 баллов)
– Верны ли утверждения?
- Сумма двух положительных чисел не может быть отрицательным числом. (Да)
- Разность двух положительных чисел не может быть отрицательным числом. (Нет)
- Произведение двух отрицательных чисел может быть отрицательным числом. (Нет)
- Частное двух отрицательных чисел не может быть положительным числом. (Нет)
– Объясните, пожалуйста, почему? (За каждый верный ответ один балл).
– Итак, что мы сделали? (Повторили правила выполнения действий с положительными и отрицательными числи)
«Не зная прошлого в развитии науки, нельзя понять её настоящее»
– Выполнять действия с отрицательными числами люди научились еще до нашей эры.
Индийские математики представляли себе положительные числа как «имущества», а отрицательные числа как «долги».
Вот как индийский математик Брахмагупта (VII в.) излагал некоторые правила выполнения действий с положительными и отрицательными числами:
«Сумма двух имуществ есть имущество»,
«Сумма двух долгов есть долг»,
«Сумма имущества и долга равна их разности»,
«Произведение двух имуществ или двух долгов есть имущество»,
«Произведение имущества и долга есть долг».
– Ребята, переведите, пожалуйста, древнеиндийские правила на современный язык.
4. Мир логики (4 баллов)
Выясните правило нахождения числа, в средней клетке первой строки, и по этому правилу найдите пропущенное число (за каждое верное число – 2 балла).
— 15
— 41
— 26
19
12
| — 18 | 6 | — 24 |
| 5 | — 12 |
Физминутка
1. Расслабьтесь, откиньтесь на спинку стула, выполните круговые вращения головой вправо – 1, 2, влево – 1, 2, 3.
2. Быстро поморгайте, закройте глаза и посидите спокойно, медленно считая до 5. Повторить 2 раза.
3. Крепко зажмурьте глаза (считая до 3), откройте их и посмотрите вдаль (считать до 5). Повторить 2 раза.
Положите руки на парту, наклоните голову, закройте глаза и пусть вам приснятся все правила выполнения действий с положительными и отрицательными числами, так как сейчас будет самостоятельная работа (считаю до 3). А теперь дети проснулись, сели правильно и приступаем к выполнению тестовых заданий.
5. Самостоятельная работа. Тест (6 баллов)
1. Какой знак надо поставить вместо *, чтобы получилось верное соотношение?
1. >; 2. ; 2.
Подведём небольшой итог нашей работе
Домашнее задание:
Найдите значение выражения:
1. 
2. – 4,1 + (– 8,3) – (– 7,3) – (+ 1,9)
1. х + 3,12 = – 5,43
2.
Найдите расстояние между точками А(– 2, 8) и В(3, 7) на координатной прямой.
Творческое задание
Составьте задачи, в результате решения которых, вы должны получить некоторые даты из истории развития своего посёлка.
Примеры таких задач мы сейчас будем решать на уроке.
Ребята, посмотрите, пожалуйста, на домашнее задание. Я думаю, что особых пояснений, по первой части работы, вам не нужно, так как, все задания подобные этим, мы с вами решали сегодня на уроке, и на предыдущих. Это задания обязательной части контрольной работы.
Ребята, а сейчас, выполняя задания по математике, мы пролистаем некоторые страницы истории Чуровской школы.
Задание 1. Решите уравнение: 2х – (– 1220) = 5000
Ребята, посмотрите, на слайде изображена лента времени, где стрелка направлена в будущее. Число 1890 я отмечаю на ленте. Дети, как вы думаете, что обозначает эта дата в истории нашей школы?
В 1890 году в селе Чуровском благодаря пожертвованиям Владыки Мисаила была открыта церковно-приходская школа, в здании, которое является исторической достопримечательностью до нашего времени. Благодарные чуровчане помнят епископа Мисаила и 16 сентября 2007 в нашем селе был открыт памятник епископу Мисаилу, в миру его звали Крылов Михаил Иванович.
Годом основания Чуровской школы, согласно архивным документам, считается 1875 год. К сожалению, приуроченное для школы здание не сохранилось до нашего времени. Ребята, под штрихом какого цвета на ленте времени нужно отметить число 1875, если длина деления между двумя белыми штрихами 20 лет? (Cиреневого)
Задание 2
В парке 100 деревьев. 3% всех деревьев составляют хвойные, остальные деревья лиственные. Сколько лиственных деревьев в парке?
1. 100 • 0,03 = 3(д) – хвойных деревьев в парке.
2. 100 – 3 = 97(д) – лиственных деревьев в парке.
Ребята, нужно выполнить перемещение по ленте времени на 97 лет от 1890 года. Какое число получилось? (1987 год)
Под штрихом, какого цвета на ленте времени нужно отметить это число? (Rрасного)
Что обозначает эта дата в истории нашей школы?
Да, действительно 1 сентября 1987 года распахнула двери новая, теперь уже средняя школа в нашем селе.
Задание 3.
Вычислите: 

Ребята, выполните, пожалуйста, перемещение по ленте времени на –24 года со дня открытия средней школы.
Какое число получилось? (1963 год)
Под штрихом, какого цвета на ленте времени нужно отметить это число? (Жёлтого)
Что обозначает эта дата в истории нашей школы?
В 1963 году Чуровская восьмилетняя школа разместилась в бывшем здании церкви святого Миколы.
Ребята, посмотрите, пожалуйста, на ленту времени. Какие вопросы вы можете задать своим одноклассникам по этой ленте времени? (Вопросы детей).
Итог урока
– Ребята, чем же мы сегодня занимались на уроке? (Ответы детей)
Вывод учителя: Сегодня на уроке, мы с вами, ребята, повторили выполнение действий с положительными и отрицательными числами, в решении примеров, уравнений и задач. Вы показали хорошие знания. Листочки с таблицами вложите в свои тетради, чтобы я могла выставить оценки в журнал. Кроме этого, немного расширили знания об истории нашей родной школы.
Рефлексия:
Ребята, на ваших столах лежат карточки. Эти же рисунки показаны на слайде. Выберите, пожалуйста, рисунок, который будет соответствовать вашему настроению после нашего занятия и я пойму, понравилось ли оно вам.
Уравнения вида -х равен a
Уравнения вида «-x равен а» появляются в 6 классе с началом изучения отрицательных чисел.
Поскольку такие уравнения в дальнейшем будут встречаться довольно часто, желательно сразу же научиться их решать правильно и быстро.
В общем виде уравнения вида «минус икс равен а» можно разбить на три случая:
Рассмотрим каждый из вариантов в общем виде и на примерах.
Решить это уравнение — значит, найти x. x и -x — противоположные числа. Поэтому икс равен числу, противоположному числу, стоящему в правой части уравнения, то есть числу которое отличается только знаком:
Рассуждая аналогично, приходим к выводу, что
Здесь минус икс равен нулю. Нуль не является ни положительным, ни отрицательным числом и противоположен самому себе, поэтому корень этого уравнения
Итак, в общем виде решение уравнений вида минус икс равен а можно записать так:
—>Школа математики для всех, кто учиться и преподает —>
Каталог статей
Положительные и отрицательные числа
Координатная прямая
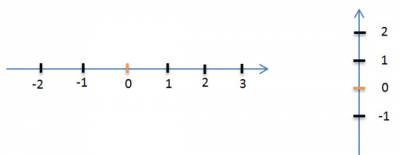
Проведём прямую. Отметим на ней точку 0 (ноль) и примем эту точку за начало отсчёта.
Укажем стрелкой направление движения по прямой вправо от начала координат. В этом направлении от точки 0 будем откладывать положительные числа.

То есть положительными называют уже известные нам числа, кроме нуля.
Иногда положительные числа записывают со знаком «+». Например, «+8».
Для краткости записи знак «+» перед положительным числом обычно опускают и вместо «+8» пишут просто 8.
Поэтому «+3» и «3» — это одно и тоже число, только по разному обозначенное.
Выберем какой-либо отрезок, длину которого примем за единицу и отложим его несколько раз вправо от точки 0. В конце первого отрезка записывается число 1, в конце второго — число 2 и т.д.

Отложив единичный отрезок влево от начала отсчёта получим отрицательные числа: -1; -2; и т.д.
Отрицательные числа используют для обозначения различных величин, таких как: температура (ниже нуля), расход — то есть отрицательный доход, глубина — отрицательная высота и другие.
Как видно из рисунка, отрицательные числа — это уже известные нам числа, только со знаком «минус»: -8; -5,25 и т.д.
- Число 0 не является ни положительным, ни отрицательным.
Числовую ось обычно располагают горизонтально или вертикально.
Если координатная прямая расположена вертикально, то направление вверх от начала отсчёта обычно считают положительным, а вниз от начала отсчёта — отрицательным.
Стрелкой указывают положительное направление.
Прямая, на которой отмечено:
• начало отсчёта (точка 0);
• единичный отрезок;
• стрелкой указано положительное направление;
называется координатной прямой или числовой осью.
Противоположные числа на координатной прямой
Отметим на координатной прямой две точки A и B, которые расположены на одинаковом расстоянии от точки 0 справа и слева соответственно.
В таком случае длины отрезков OA и OB одинаковы.
Значит, координаты точек A и B отличаются только знаком. 
Также говорят, что точки A и B симметричны относительно начала координат.
Координата точки A положительная «+2», координата точки B имеет знак минус «-2».
A (+2), B (-2).
- Числа, которые отличаются только знаком, называются противоположными числами. Соответствующие им точки числовой (координатной) оси симметричны относительны начала отсчёта.
Каждое число имеет единственное противоположное ему число. Только число 0 не имеет противоположного, но можно сказать, что оно противоположно самому себе.
Запись «-a» означает число, противоположное «a». Помните, что под буквой может скрываться как положительное число, так и отрицательное число.
Пример:
-3 — число противоположное числу 3.
Записываем в виде выражения:
-3 = -(+3)
Пример:
-(-6) — число противоположное отрицательному числу -6. Значит, -(-6) это положительное число 6.
Записываем в виде выражения:
-(-6) = 6
Сложение отрицательных чисел
Сложение положительных и отрицательных чисел можно разобрать с помощью числовой оси.
Сложение небольших по модулю чисел удобно выполнять на координатной прямой, мысленно представляя себе как точка, обозначающая число передвигается по числовой оси.
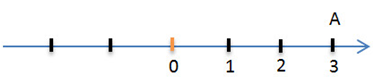
Возьмём какое-нибудь число, например, 3. Обозначим его на числовой оси точкой A.
Прибавим к числу положительное число 2. Это будет означать, что точку A надо переместить на два единичных отрезка в положительном направлении, то есть вправо . В результате мы получим точку B с координатой 5.
3 + (+ 2) = 5

Для того чтобы к положительному числу, например, к 3 прибавить отрицательное число (- 5), точку A надо переместить на 5 единиц длины в отрицательном направлении, то есть влево .
В этом случае координата точки B равна — 2.
Итак, порядок сложения рациональных чисел с помощью числовой оси будет следующим:
• отметить на координатной прямой точку A с координатой равной первому слагаемому;
• передвинуть её на расстояние, равное модулю второго слагаемого в направлении, которое соответствует знаку перед вторым числом (плюс — передвигаем вправо, минус — влево);
• полученная на оси точка B будет иметь координату, которая будет равна сумме данных чисел.
Двигаясь от точки — 2 влево (так как перед 6 стоит знак минус), получим — 8.
— 2 + (- 6) = — 8
Сложение чисел с одинаковыми знаками
Складывать рациональные числа можно проще, если использовать понятие модуля.
Пускай нам нужно сложить числа, которые имеют одинаковые знаки.
Для этого, отбрасываем знаки чисел и берём модули этих чисел. Сложим модули и перед суммой поставим знак, который был общим у данных чисел.
Пример.

Пример сложения отрицательных чисел.
(- 3,2) + (- 4,3) = — (3,2 + 4,3) = — 7,5
- Чтобы сложить числа одного знака надо сложить их модули и поставить перед суммой знак, который был перед слагаемыми.
Сложение чисел с разными знаками
Если числа имеют разные знаки, то действуем несколько по-иному, чем при сложении чисел с одинаковыми знаками.
• Отбрасываем знаки перед числами, то есть берём их модули.
• Из большего модуля вычитаем меньший.
• Перед разностью ставим тот знак, который был у числа с бóльшим модулем.
Пример сложения отрицательного и положительного числа.
0,3 + (- 0,8) = — (0,8 — 0,3) = — 0,5
Пример сложения смешанных чисел.
Чтобы сложить числа разного знака надо:
• из бóльшего модуля вычесть меньший модуль;
• перед полученной разностью поставить знак числа, имеющего больший модуль.
Вычитание отрицательных чисел
Как известно вычитание — это действие, противоположное сложению.
Если a и b — положительные числа, то вычесть из числа a число b, значит найти такое число c, которое при сложении с числом b даёт число a.
a — b = с или с + b = a
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.
- Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Или по другому можно сказать, что вычитание числа b — это тоже самое сложение, но с числом противоположным числу b.
a — b = a + (- b)
Пример.
6 — 8 = 6 + (- 8) = — 2
Пример.
0 — 2 = 0 + (- 2) = — 2
- Стоит запомнить выражения ниже.
- 0 — a = — a
- a — 0 = a
- a — a = 0
Правила вычитания отрицательных чисел
Как видно из примеров выше вычитание числа b — это сложение с числом противоположным числу b.
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти разность двух чисел.
Разность может быть положительным числом, отрицательным числом или числом ноль.
Примеры вычитания отрицательных и положительных чисел.
• — 3 — (+ 4) = — 3 + (- 4) = — 7
• — 6 — (- 7) = — 6 + (+ 7) = 1
• 5 — (- 3) = 5 + (+ 3) = 8
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (+ a) = + a
Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
— (+ a) = — a
Из равенств видно, что если перед и внутри скобок стоят одинаковые знаки, то получаем «+», а если знаки разные, то получаем «-».
(- 6) + (+ 2) — (- 10) — (- 1) + (- 7) = — 6 + 2 + 10 + 1 — 7 = — 13 + 13 = 0
Правило знаков сохраняется и в том случае, если в скобках не одно число, а алгебраическая сумма чисел.
a — (- b + c) + (d — k + n) = a + b — c + d — k + n
Обратите внимание, если в скобках стоит несколько чисел и перед скобками стоит знак «минус», то должны меняться знаки перед всемичислами в этих скобках.
Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел
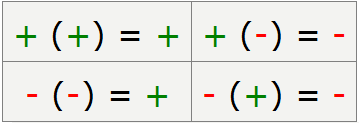
Или выучить простое правило.
- Минус на минус даёт плюс,
- Плюс на минус даёт минус.
Умножение отрицательных чисел
Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.
Умножение чисел с одинаковыми знаками
Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.
Чтобы умножить два числа с одинаковыми знаками надо:
• перемножить модули чисел;
• перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).
Примеры умножения отрицательных и положительных чисел.
• (- 3) • (- 6) = + 18 = 18
• 2 • 3 = 6
Умножение чисел с разными знаками
Второй возможный случай — это умножение чисел с разными знаками.
Чтобы умножить два числа с разными знаками, надо:
• перемножить модули чисел;
• перед полученным произведением поставить знак «-».
Примеры умножения отрицательных и положительных чисел.
• (- 0,3) • 0,5 = — 1,5
• 1,2 • (- 7) = — 8,4
Правила знаков для умножения
Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.
- Минус на минус даёт плюс,
- Плюс на минус даёт минус.

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.
При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.
Пример.
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =
В примере пять отрицательных множителей. Значит, знак результата будет «минус».
Теперь вычислим произведение модулей, не обращая внимание на знаки.
6 • 3 • 4 • 2 • 12 • 1 = 1728
Конечный результат умножения исходных чисел будет:
(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = — 1728
Умножение на ноль и единицу
Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.
• 0 • a = 0
• a • 0 = 0
• a • 1 = a
Примеры:
• 0 • (- 3) = 0
• 0,4 • 1 = 0,4
Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).
- При умножении на (- 1) число меняется на противоположное.
В буквенном выражении это свойство можно записать:
a • (- 1) = (- 1) • a = — a
При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.
Пример умножения отрицательных и положительных чисел.
Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если a и b положительные числа, то разделить число a на число b, значит найти такое число с, которое при умножении на b даёт число a.
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число (- 15) на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число (- 15). Таким числом будет (- 3), так как
(- 3) • 5 = — 15
Примеры деления рациональных чисел.
1. 10 : 5 = 2, так как 2 • 5 = 10
2. (- 4) : (- 2) = 2, так как 2 • (- 2) = — 4
3. (- 18) : 3 = — 6, так как (- 6) • 3 = — 18
4. 12 : (- 4) = — 3, так как (- 3) • (- 4) = 12
Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками — число отрицательное (примеры 3,4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «+».
Примеры деления чисел с одинаковыми знаками:
• (- 9) : (- 3) = + 3
• 6 : 3 = 2
Чтобы разделить два числа с разными знаками, надо:
• модуль делимого разделить на модуль делителя;
• перед результатом поставить знак «-».
Примеры деления чисел с разными знаками:
• (- 5) : 2 = — 2,5
• 28 : (- 2) = — 14
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби
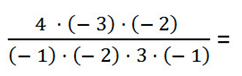
Можно обратить внимание, что в числителе 2 знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
- Частное от деления нуля на число, отличное от нуля, равно нулю.
- 0 : a = 0, a ≠ 0
- Делить на ноль НЕЛЬЗЯ!
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
• а : 1 = a
• а : (- 1) = — a
• а : a = 1
, где а — любое рациональное число.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
• если a • b = с; a = с : b; b = с : a;
• если a : b = с; a = с • b; b = a : c
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.
Пример нахождения неизвестного.
x • (- 5) = 10
Знак «минус» в дробях
Разделим число (- 5) на 6 и число 5 на (- 6).
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, и запишем частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
• перед дробью;
• в числителе;
• в знаменателе.
- При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
http://www.for6cl.uznateshe.ru/uravneniya-x-raven-a/
http://matematik.3dn.ru/publ/3-1-0-44