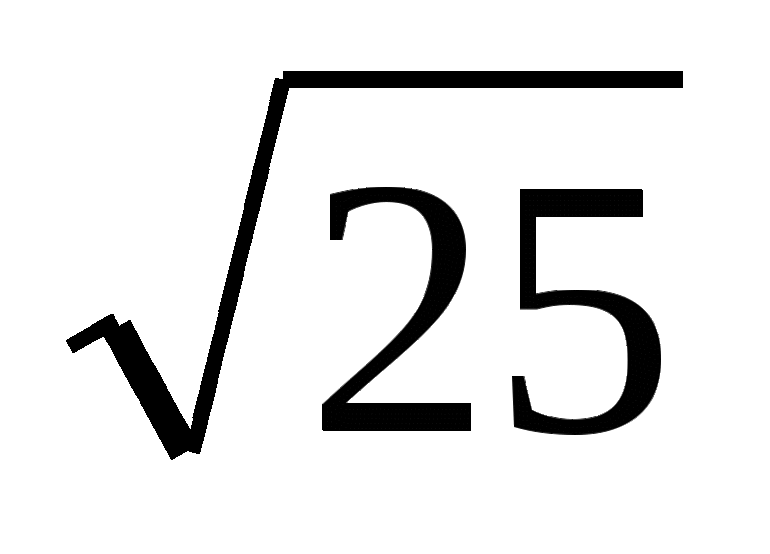Уравнения с параметрами и корнем четвертой степени

Алгебраические уравнения высших степеней с параметрами

Разделы: Математика

1.1. Общая методическая концепция решения уравнений с параметрами

Пусть дано уравнение F(x, a) = 0, (1)

если ставится задача для каждого значения а А решить уравнение (1) относительно х, т.е. получить уравнение

то уравнение (1) называется уравнением с неизвестным х и параметром а. А – область изменения параметра. Принято считать, что А – множество действительных чисел. Решить уравнение (1) – значит решить множество уравнений, которые получаются из уравнения (1) при а R. Сделать это можно, если по некоторому признаку разбить множество А на подмножества и решить заданное уравнение на каждом из них. Значения а называются контрольными.

1.2. Использование параметра как равноправной переменной

Некоторые уравнения бывает целесообразно решать, рассматривая их как уравнение именно относительно параметра, который фигурирует в условии, а не относительно искомой переменной. Этот путь эффективен, в частности, в тех случаях, когда степень переменной относительно высока, а степень параметра равна двум.

Пример 1. Решить уравнение с параметром.

2x 3 – (а+2)х 2 – ах + а 2 = 0 (1)

Решение: Данное уравнение можно рассматривать как квадратное относительно параметра а, переписав его в виде:

а 2 – х(х+1)а – 2х 2 + 2х 3 = 0 (2)

Найдем дискриминант D.

D = х 2 (х+1) 2 – 8(х 3 – х 2 ) = х 4 — 6х 3 + 9х 2 = х 2 (х 2 — 6х + 9) = х 2 (х — 3) 2 .

Найдем корни уравнения (2).

; а₂ = 2х.

Получим уравнение (а – х 2 + х)(а – 2х) = 0 равносильное исходному уравнению, которое ещё в свою очередь равносильно совокупности

Рассмотрим уравнение х 2 – х – а = 0, D = 1 – 4а.

D = 0 при а = -1/4 один корень х = 1/2

D 0 при а > -1/4 два корня

Рассмотрим уравнение х = а/2, при а = -1/4, х = -1/8.

Ответ: при а > -1/4 три корня: х1 = а/2,

при а = -1/4 два корня: х1 = -1/8; х 2 = ½

при а 4 – (а+2)х 3 – (а – 1)х 2 + (а 2 – 1) = 0;

1.3. Графический способ решения уравнений с параметрами

Взгляд на параметр как на равноправную переменную находит свое отражение в графических методах. В самом деле, поскольку параметр «равен в правах» с переменной, то ему, естественно можно выделить и свою координатную ось. Таким образом, возникает координатная плоскость (х; а). Рассмотрим примеры.

Пример 1. В зависимости от параметра а определить число корней уравнения.

x 4 – 10х 3 – 2(а — 11)х 2 + 2(5а + 6)х + 2а + а 2 = 0;

Решение. Рассмотрим это уравнение как квадратное относительно а.

а 2 + 2а(1 + 5х – х 2 ) + (х 4 – 10х 3 + 22х 2 + 12х) = 0;

D/4 = 1 + 25х 2 + х 4 + 10х – 10х 3 – 2х 2 – х 4 + 10х 3 – 22х 2 – 12х = х 2 – 2х +1 = = (х – 1) 2

Найдем а₁ и а₂ ; а₁ = х 2 -5х – 1 + х – 1 = х 2 — 4х – 2;

а₂ = х 2 -5х – 1 — х + 1 = = х 2 – 6х.

Теперь обращаемся к координатной плоскости (х; а).

х 2 — 4х – 2 = х 2 – 6х, 2х = 2, х = 1, а(1) = -5.

Ответ: если а -5, то четыре решения.

Упражнения

Найти все значения параметра а, при каждом из которых уравнение имеет три решения.

1. (х 2 – 12а) 2 – 24х 2 + 32х + 96а = 0;
2. (2х 2 – а) 2 – 24х 2 + 16х + 4а = 0;
3. (2х 2 – а) 2 = 13х 2 + 6х – 2а = 0.

1.4. Использование свойств функций для решения алгебраических уравнений

На выпускных экзаменах за курс средней школы встречаются уравнения с параметром, решение которых связано с использованием четности функций. Напомним определение четности функции.

Определение. Функция f(x) называется четной, если f(-x) = f(x) для любого х из области определения этой функции. График четной функции симметричен относительно оси ординат. У четной функции область определения симметрична относительно начала координат.

Пример 1. Может ли при каком-нибудь значении а уравнение

2х 8 – 3ах 6 + 4х 4 – ах 2 = 5 иметь 5 корней?

Решение. Обозначим f(x) = 2х 8 – 3ах 6 + 4х 4 – ах 2 . f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х₀ – тоже, х = 0 не является корнем данного уравнения (0 ≠ 5). Следовательно, число корней у этого уравнения при любом действительном а четно, поэтому 5 корней оно иметь не может.

Пример 2. При каком значении а уравнение х 10 – а|х| + a 2 – а = 0 имеет единственное решение?

Решение. Обозначим f(x) = х 10 – а|х| + a 2 – а, f(x) – функция четная, поэтому, если х0 – корень данного уравнения, то – х₀ – тоже. Значит для единственности решения необходимо, чтобы х₀ = 0. В этом случае из уравнения получим: a 2 – а = 0, а = 0 или а = 1. Проверим достаточность каждого из полученных значений параметра а,

при а = 0, х 10 = 0, т.е. х = 0 единственное решение.

при а = 1, х 10 — |x| = 0. Корнями являются числа ± 1, 0.

Ответ: при а = 0 уравнение имеет единственное решение.

Упражнения

1. Может ли при каком-нибудь а уравнение 2х 6 – х 4 – ах 2 = 1 иметь три корня?
2. Может ли при каком-нибудь а уравнение 2х 6 – 2ах 4 + 3х 2 = 4 иметь пять корней?
3. При каком значении а уравнение имеет единственное решение?

1.5. Метод замены

Как мы уже знаем, что рациональное и быстрое решение уравнения зависит от замены переменной. Рассмотрим примеры, для решения которых нужны специальные замены, которые приводят как раз к быстрому решению уравнений.

Пример 1. Решить уравнение (х + 2а)(х +3а)(х + 8а)(х + 12а) = 4а 2 х 2 ,

где а – параметр.

Решение. Данное уравнение относится к уравнению вида

(х + а)(х +b)(х + c)(х + d) = Eх 2 (см. п. 2.5 (3))

Используя специфику решения такого уравнения, будем иметь:

(х 2 + 14ах +24а 2 )( х 2 + 11ах +24а 2 ) = 4а 2 х 2

Если а = 0, то х = 0.

Обратно, если а ≠ 0, то х ≠ 0.

Разделим обе части этого уравнения на а 2 х 2 , будем иметь

В полученном уравнении сделаем подстановку и получим уравнение (у + 14)(у + 11) = 4, у 2 + 25у + 150 = 0, у₁ = — 15, у₂ = — 10.

Таким образом, получим два уравнения

и

Решим первое уравнение х 2 + 15ах + 24а 2 = 0, D = 129a 2 , х_1,2

Решим второе уравнение х 2 + 10ах + 24а 2 = 0, D = 4a 2

х 3 = -6а, х 4 = -4а

Ответ: если а = 0, то х = 0
если а ≠ 0, то х_1,2, х 3 = -6а, х 4 = -4а

Упражнения

1. Найдите все действительные значения величины а, при которых уравнение х(х +1)(х + а)(х + 1 + а) = а 2 имеет четыре действительных корня.
2. Решить уравнение х 4 + а 4 – 3ах 3 + 3а 2 х = 0.
3. При каких значениях а уравнение (х 2 – 2х) 2 — (а + 2)(х 2 – 2х) + 3а – 3 = 0 имеет четыре корня?
4. Решить уравнение (х + а)(х + 2а)(х + 3а)(х + 4а) = 3а 4

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .

Для решения этого типа уравнений применяются формулы сокращенного умножения:

A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0

Остается лишь найти корни квадратных трехчленов.

Решить уравнение четвертой степени 4 x 4 + 1 = 0 .

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )

Теперь найдем корни квадратных трехчленов.

2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i

2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i

Мы получили четыре комплексных корня.

Ответ: x = 1 2 ± i и x = — 1 2 ± i .

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :

A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2

2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0

Решим полученное квадратное уравнение:

D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3

Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .

Решим первое уравнение:

x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4

Решим второе уравнение:

x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2

Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.

Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .

Решение

Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:

2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3

Следовательно, x 2 = 1 2 или x 2 = — 3 .

Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .

Ответ: x = ± 1 2 и x = ± i · 3 .

Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9

Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .

Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .

Решение

Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0

Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .

Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0

x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0

x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0

Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .

Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

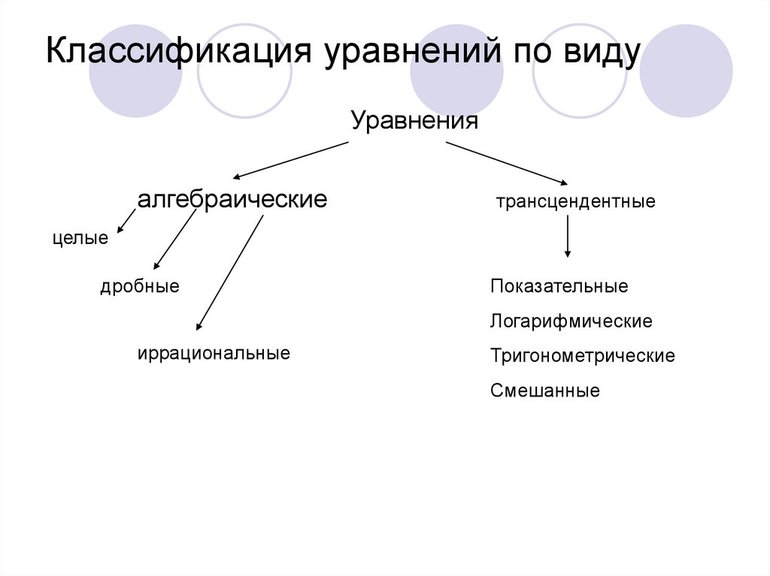
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

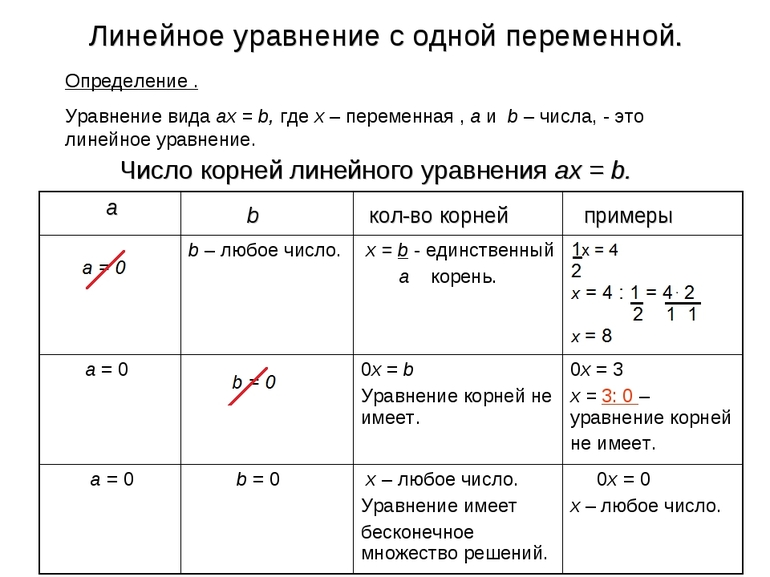
Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.