Уравнения с параметром 8 класс объяснение

Урок алгебры по теме «Уравнения с параметром». 8-й класс

Разделы: Математика

Класс: 8

Цели: изучить понятие «уравнения с параметром», сформировать умение решать линейные и квадратные уравнения с параметром.

Место урока в рабочей программе:

Провести либо перед контрольной работой №6 «Дробно-рациональные уравнения», либо после нее.

Урок проводить в классе с хорошей математической подготовкой. Для учащихся, которые учатся на «3», можно подготовить индивидуальные задания, с целью исправления ошибок из контрольной работы.

Ход урока

I. Проверка домашнего задания (Приложение 1, слайды 2-14).

1) Карточки, которые раздавались учащимся на предыдущем уроке. (Приложение 2).

2) Из учебника № 703

II. Введение в тему урока.

Решите кроссворд. Задания зачитываются учителем. Проверка (Приложение 1, слайды 15-16)

1. Графиком квадратичной функции является …

2. Равенство, содержащее переменную, значение которой надо найти – это …

3. Квадратное уравнение, в котором коэффициент при х 2 равен 1 называется…

4. Уравнения, в которых левая и правая части являются рациональными выражениями, называются…

5. Запись какого-нибудь правила с помощью букв – это…

6. Графиком функции у=k/x, где х≠0, является…

7. Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носит название теоремы…

8. Уравнение вида ах 2 + вх + с = 0, где х – переменная, а, в и с – некоторые числа, причем а≠0 называется… .

Записали тему урока. (Приложение 1, слайд 17)

Сколько может иметь корней линейное уравнение в зависимости от коэффициентов? А квадратное?

III. Объяснение нового материала.

1. Изучение понятия «уравнение с параметром».

Во время актуализации знаний учащиеся вспомнили, что линейное уравнение в зависимости от коэффициентов может иметь одно решение, бесконечно много решений, либо не иметь решений. Так же и квадратное уравнение в зависимости от дискриминанта, а значит, от коэффициентов, может иметь один корень, два корня, либо не иметь корней.

(Приложение 1, слайд 18)

Определение. Уравнение вида f(а,в,с …,х) =0, переменные а,в,с … которые при решении уравнения являются постоянными называются параметрами, а само уравнение , уравнением с параметрами.

Если уравнение записано в виде равенства двух выражений, в запись которых входят две буквы, например ах = 5, то нужно четко определить, что это за уравнение. Различают три смысла:

1) х, а – равноценные переменные. Говорят, что задано уравнение с двумя переменными и требуется найти все пары (х, а), которые удовлетворяют данному уравнению.

2) х – переменная, а – фиксированное число. Говорят, что задано уравнение с одной переменной х и требуется найти значение х, удовлетворяющее уравнению при фиксированном значении а.

3) х – переменная, а – любое число из некоторого множества А. Говорят, что задано уравнение с переменной х и параметром а (А – множество изменения параметра), требуется решить уравнение относительно х для каждого значения а.

Область изменения параметра либо оговаривается заранее, либо обычно подразумевается множество всех действительных чисел.

Тогда задачу решения уравнения с параметром можно переформулировать: решить семейство уравнений, получаемых из уравнения при любых действительных значениях параметра.

2. Примем решения уравнения с параметром.

Ясно, что выписать каждое уравнение из бесконечного семейства уравнений невозможно. Тем не менее, каждое уравнение семейства должно быть решено. Сделать это можно, если по некоторому целесообразному признаку разбить множество всех значений параметра на подмножества и решить затем заданное уравнение на каждом из этих подмножеств.

Для разбиения множества значений параметра на подмножества удобно воспользоваться теми значениями параметра, при которых или при переходе через которые происходят качественные изменения уравнения. Такие значения параметра называются контрольными.

3. Алгоритм решения уравнения с параметром:

1-й ш а г. Находим область изменения параметра.

2-й ш а г. Находим ОДЗ уравнения.

3-й ш а г. Определяем контрольные значения параметра и разбиваем область изменения параметра на подмножества.

4-й ш а г. Решаем уравнение на каждом подмножестве области изменения параметра.

5-й ш а г. Записываем ответ.

4. Решение линейных и квадратных уравнений с параметром.

На примерах со с. 141–143 учебника рассмотреть, как обнаруживаются контрольные значения параметра, как с их помощью множество значений параметра разбивается на подмножества и как затем на каждом из подмножеств решается заданное линейное или квадратное уравнение.

IV. Формирование умений и навыков.

Все упражнения, относящиеся к этому пункту, можно разбить на 3 группы:

1) решить уравнение с параметром, заданное в стандартном виде;

2) преобразовать уравнение с параметром и решать его;

3) найти значения параметра, при которых будет выполняться некоторое условие.

1. № 641 (а) (Разбирает учитель вместе с учениками).

Если р = 0, то уравнение примет вид –1 = 0.

Данное уравнение не имеет корней.

О т в е т: при р = 0 нет корней; при р ≠ 0; у = (p + 1)/p.

2. № 642 (Учащийся, который сам вызвался к доске).

Если а – 2 = 0, то есть а = 2, то

Если а – 2 ≠ 0, то есть а ≠ 2, то х = (a-2)(a 2 -9)/(a-2),

О т в е т: при а = 2 х – любое; при а ≠ 2 х = а 2 – 9.

№ 644 (б) (Проводится анализ, а затем записываем).

Если а ≠ 0, то D > 0 и

3. № 646 (Проводим анализ и даем время решить самостоятельно, а затем, проверяем).

х₁ 2 + х₂ 2 принимает наименьшее значение при а = 1 и равно 5.

О т в е т: 5 при а = 1.

V. Физкультминутка (Приложение 3, Приложение 4, Приложение 1, слайд 20)

VI. Обучающая самостоятельная работа.

№645(б) – I вариант, №645 (г) – II вариант.

Двое учащихся на откидных досках. Оценки только тем учащимся, которые написала на «5».

VII. Итог урока

1. Какие уравнения мы сегодня изучили?
2. Какое уравнение называются уравнением с параметром? (Слайд с определением). Приведите свои примеры.
3. Уравнения с параметрами встречаются в экзаменах 9 и 11 классов. (Можно предложить на дом задания из ГИА).

VIII. Домашнее задание. (Приложение 1, слайд 22)

Прочитать п.27 и разобрать примеры 1 и 2, №645 (а, в), №704.

Информационные ресурсы:

1. Алгебра, 8 класс: учеб. для общеобразоват. учреждений / [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под ред. С.А. Теляковского. – 19-е изд. – М.: Просвещение, 2010.
2. Алгебра 8 класс. Задания для обучения и развития учащихся./ ЛебединцкваЕ.А., Беленкова Е.Ю. – М.: Интелект-Центр, 2007.
3. Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворовой (компакт-диск) – издательство «Учитель». 2011.
4. Интернет-ресурсы.

Урок по алгебре в 7,8 классе «Линейное уравнение с параметром и его решение в общем виде»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Тема: Линейное уравнение с параметром и его решение в общем виде.

Образовательные: дать определение линейного уравнения с параметром, рассмотреть способы его решения, схему исследования линейных уравнений с параметрами. Формировать навыки решения линейных уравнений с параметрами.

Развивающие: развивать уровень математического и логического мышления, первоначальные навыки исследовательской деятельности.

Воспитательные: формирование волевые качества, формирование коммуникабельность, выработка объективной оценки своих достижений, формирование ответственности.

Поприветствовать учащихся, проверить их готовность к уроку, объявить тему урока и цель урока.

II . Проверка домашнего задания.

ученики записывают на доске решения уравнений;

обсуждение, замечания, уточнения к решениям на доске.

III . Актуализация опорных знаний учащихся.
№1. Решить уравнение: m х – 7 = — 1.

Если m = 0, то уравнение примет вид 0 • m = 6 и не имеет решений;

Если m ≠ 0, то уравнение примет вид х = и имеет единственное решение.

Ответ: при m = 0 нет решений; при m ≠ 0 х = .

№ 2. При каком значении b уравнение |х| + b = 0 не будет иметь корней?

Решение: = — b ;

Если b = 0, то уравнение примет вид |х| = 0, т.е. х = 0 и имеет ед. решение;

Если b > 0, то уравнение не имеет решений;

Если b b , т.е. х = ± b и имеет два корня.

IV . Объяснение нового материала.

1. Определение линейного уравнения с параметром.

Уравнение вида Ах = В, (1)

где А, В — выражения, зависящие от параметров, ах- неизвестное,

называется линейным уравнением с параметрами.

2. что значит решить уравнение с параметрами?

Решить уравнение с параметрами — значит указать, при каких допустимых значениях параметров существуют решения, выяснить их число, каковы они; кроме того, обычно при решении уравнений с параметрами необходимо выяснить, при каких допустимых значениях параметров решений нет.

в) способы решения линейного уравнения.

Линейные уравнения с параметром решаются двумя способами: аналитическим и графическим.

Графический способ решения линейного уравнений с параметром удобен тогда, когда нужно определить количество корней уравнения.

Аналитический способ решения линейного уравнения с параметром удобен тогда, когда требуется найти решение уравнения при каждом значении параметра.

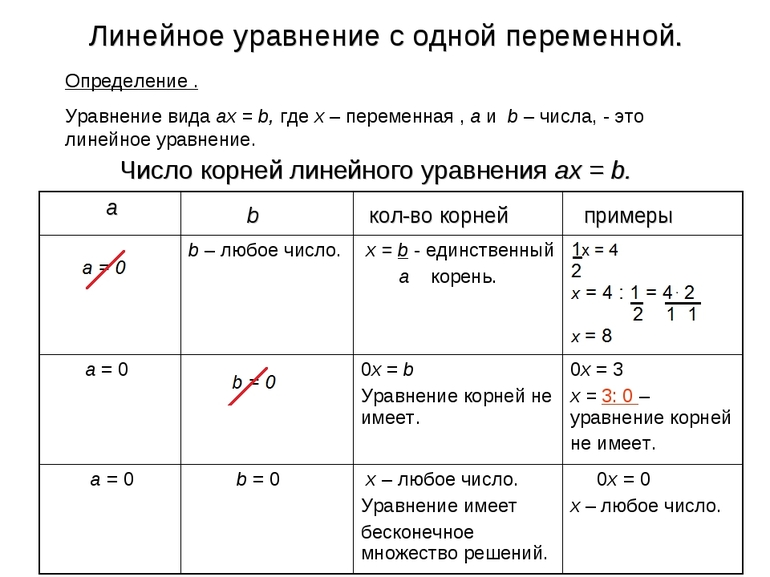
г) схема исследования линейного уравнения (1).

1. Если А = 0, В ≠ 0 , то уравнение (1) примет вид 0 • х = В и не имеет решений;

2. Если А = 0, В = 0, то уравнение (1) примет вид 0 • х = 0 и имеет бесконечное
множество решений (х — любое число);

3. Если А ≠ 0 , В — любое, то уравнение (1) имеет единственное решение х = .

Замечание. Если линейное уравнение не представлено в виде (1), то сначала нужно привести его к виду (1) и только после этого проводить исследование.

V . Формирование умений и навыков учащихся.

№ 1. Решить уравнение: а) (а + 3)х =5.

Если а + 3 = 0, т.е. а = -3, то уравнение примет вид 0 • х = 5 и не имеет решений;

Если а + 3 ≠ 0 , т.е. а ≠ -3, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = -3 нет решений; при а ≠ -3 х =.

Если а – 6 = 0, т.е. а = 6, то уравнение примет вид 0 • х = -2 и не имеет решений;

Если а – 6 ≠ 0 , т.е. а ≠ 6, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = 6 нет решений; при а ≠ 6 х = .

№ 2. Решить уравнение: а) (а + 4)х = 2а +1.

Если а + 4 = 0, т.е. а = -4, то уравнение примет вид 0 • х = -7 и не имеет решений;

Если а + 4 ≠ 0, т.е. а ≠ -4, то уравнение примет вид х = и имеет ед. решение.

Ответ: при а = -4 нет решений; при а ≠ -4 х = .

Если а — 1 = 0, т.е. а = 1, то уравнение примет вид 0• х = -1 и не имеет решений;

Если а — 1 ≠ 0, т.е. а ≠ 1, то уравнение примет вид х = и имеет ед. решение. Ответ: при a = 1 нет решений; при а ≠ 1 х =.

№ 3. Решить уравнение: а) (а + 1)х = а + 1.

Если а + 1 = 0, т.е. а = -1, то уравнение примет вид 0 • х = 0 и имеет бесконечное множество решений (х — любое число);

Если а + 1 ≠ 0 , т.е. а ≠ -1, то уравнение примет вид х =, х = 1 и имеет ед. решение.

Ответ: при а = -1 х — любое число; при а ≠ -1 х = 1.

Если а – 4 = 0, т.е. а = 4, то уравнение примет вид 0 • х = 0 и имеет бесконечное

множество решений (х — любое число);

Если а – 4 ≠ 0 , т.е. а ≠ 4, то уравнение примет вид х =, х = -1 и имеет ед. решение.

Ответ: при а = 4 х — любое число; при а ≠ 4 х = -1.

№ 4. Решить уравнение: а) (а – 7)х = а(а – 7).

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное

множество решений (х — любое число);

Если а – 7 ≠ 0 , т.е. а ≠ 7, то уравнение примет вид х =, х = а и имеет ед. решение.

Ответ: при a = 7 х — любое число; при а ≠ 7 х = а.

б) (а+5)х = (а + 5)(а – 2).

Если а + 5 = 0, т.е. а = -5, то уравнение примет вид 0 • х = 0 и имеет бесконечное

множество решений (х — любое число);

Если а + 5 ≠ 0 , т.е. а ≠ -5, то уравнение примет вид х = , х = а – 2 и

имеет ед. решение.

Ответ: при a = -5 х — любое число; при a ≠ -5 x = a – 2.

№ 5. Решить уравнение (а – 7)х = а 2 – 14а + 49.

Решение: (а – 7)х = (а – 7) 2 .

Если а – 7 = 0, т.е. а = 7, то уравнение примет вид 0 • х = 0 и имеет бесконечное

множество решений (х — любое число);

Если а – 7 ≠ 0 , т.е. а ≠ 7, то уравнение примет вид х =, х = а – 7 и имеет единственное решение.

Ответ: при а = 7 х — любое число; при а ≠ 7 х = а – 7.

VI . Подведение итогов урока.

Что нового сегодня Вы узнали на уроке? Дайте определение линейного уравнения с параметрами. Что значит решить уравнение с параметром? Назовите способы решения и схему исследования линейного уравнения с параметром.

VII . Домашнее задание.

Решить уравнения: а) (а – 9)х = 4; б) (а – 6)х = а + 8; в) (а + 3)х = а + 3;

г) (а + 2)х = (а + 2)(а – 3); г) (а + 3)х = а 2 + 6а + 9.

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

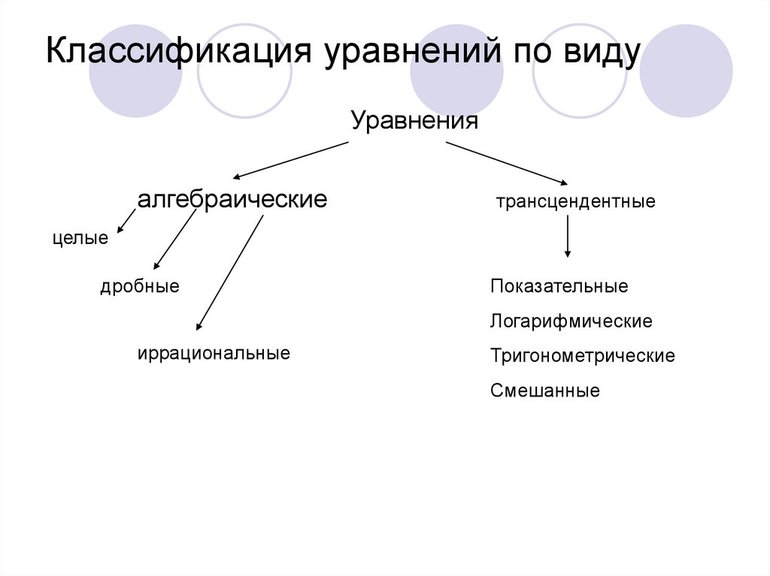
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

1. Линейные.
2. Квадратные (квадратичные).
3. Кубические.
4. Биквадратные.
5. Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

1. Записывается искомое выражение.
2. При необходимости раскрываются скобки и приводятся подобные элементы.
3. Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
4. Правая часть сокращается на коэффициент при неизвестной.
5. Записывается результат.
6. Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

1. Записать выражение.
2. Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
3. Вычислить значение D (D 0 — два решения).
4. При D=0 формула корня имеет такой вид: t=-В/(2А).
5. Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
6. Записать результат.
7. Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

1. Приводятся подобные элементы: 3v=0.
2. Находится корень: v=0.
3. Приравнивается к выражению, которое заменяли: t 3 −2=0.
4. Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
5. Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

1. Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
2. Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
3. Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
4. Результат: m1=-3 и m2=3.
5. Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

1. Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
2. Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
3. Ввести замену v 4 −16=m: m+4p+4=0.
4. Вывести формулу нахождения параметра: р=-(m/4)-1.
5. Подставить величину m: р=-1-(v 4 +16)/4.
6. C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
7. Корни: v1=[12]^(¼) и v2=-[12]^(¼).
8. Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
9. Результат: v1=[12]^(¼).
10. Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.