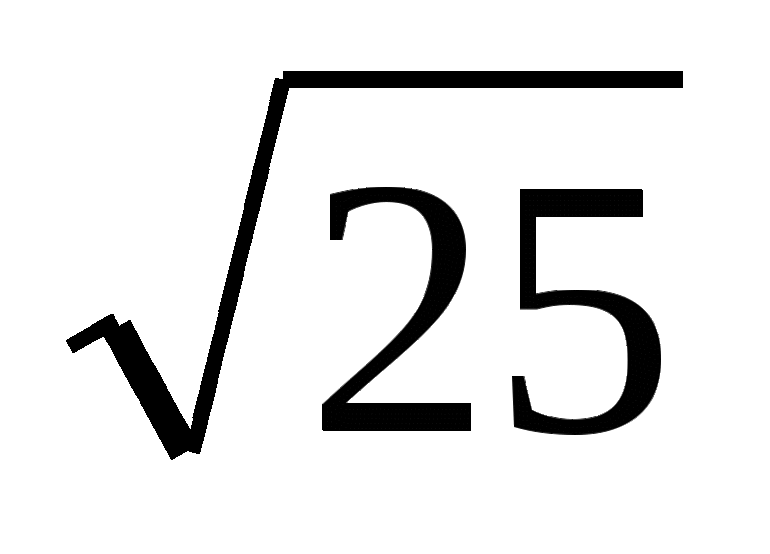Уравнения с параметром какой класс

Уравнения с параметром

Разделы: Математика

Справочный материал

Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.

Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.

Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет

Если 1 – а 0, т.е. а 1, то х =

Пример 4.

Если а = 1, то 0х = 0
х – любое действительное число

Если а = -1, то 0х = -2
Корней нет

Если а 1, а -1, то х = (единственное решение).

Это значит, что каждому допустимому значению а соответствует единственное значение х.

если а = 5, то х = = ;

Дидактический материал

3. а = +

4. + 3(х+1)

5. = –

6. =

Ответы:

При а1 х =;

При а3 х = ;

При а1, а-1, а0 х = ;

при а = 1 х – любое действительное число, кроме х = 1

При а2, а0 х = ;

При а-3, а-2, а0, 5 х =

При а + с0, с0 х = ;

Квадратные уравнения с параметром

Пример 1. Решить уравнение

х = –

В случае а 1 выделим те значения параметра, при которых Д обращается в нуль.

Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16

a =

Если а -4/5 и а 1, то Д > 0,

х =

х = – = –

Пример 2. При каких значениях параметра а уравнение

х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?

В итоге

4(а – 1)(а – 6) > 0
— 2(а + 1) 0

а 6
а > — 1
а > 5/9

Пример 3. Найдите значения а, при которых данное уравнение имеет решение.

Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а

4а 2 – 16 0

4а(а – 4) 0

а(а – 4)) 0

Ответ: а 0 и а 4

Дидактический материал

1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?

2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?

3. При каких значениях а уравнение (а 2 – 6а + 8) х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?

4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?

5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?

Показательные уравнения с параметром

Пример 1.Найти все значения а, при которых уравнение

9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.

Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение

3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)

Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или

Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log₃2 , или х 2 – хlog₃2 + 1 = 0.

Это уравнение не имеет действительных корней, так как его Д = log 2 ₃2 – 4 х+1/х = а то х + 1/х = log₃а, или х 2 – хlog₃а + 1 = 0. (3)

Уравнение (3) имеет ровно два корня тогда и только тогда, когда

Д = log 2 ₃2 – 4 > 0, или |log₃а| > 2.

Если log₃а > 2, то а > 9, а если log₃а 9.

Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?

Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х₁ = -3, х₂ = а = >

а – положительное число.

Дидактический материал

1. Найти все значения а, при которых уравнение

25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.

2. При каких значениях а уравнение

2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?

3. При каких значениях параметра а уравнение

4 х — (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?

Ответ:

0 25/2
при а = 1, а = -2,2
0 0, х1/4 (3)

х = у

Если а = 0, то –

2у + 1 = 0
2у = 1
у = 1/2

х = 1/2
х = 1/4

Не выполняется (2) условие из (3).

Пусть а 0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а 0, т.е. при а 1.

Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).

Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х

Выражая х из (1) и подставляя в (2), получаем неравенство

2 – а > 1 – а (3)

Чтобы решить неравенство (3), построим графики функций у = 2 – а и у = 1 – а.

Решения неравенства (3) образуют промежуток (а₀; 2), где а₀ 2

а₀ =

Ответ: x + 9a 3 ) = x имеет ровно два корня.

Найдите, при каких значениях а уравнение log ₂ (4 x – a) = x имеет единственный корень.

При каких значениях а уравнение х – log ₃ (2а – 9 х ) = 0 не имеет корней.

Ответы:

Задачи с параметрами в курсе основной школы

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Задачи с параметрами в курсе основной школы

2. Цели и задачи работы

3. Методические разработки по классам

4. Используемая литература

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры учащихся. Решение задач с параметрами открывает перед учениками большое число эвристических приемов общего характера, ценных для математического развития, применимых в исследованиях и в любом другом математическом материале. Они имеют принципиально исследовательский характер, и с этим связаны как методическое значение таких задач, так и трудности выработки навыков их решения. Именно в терминах параметров происходит описание свойств математических объектов: функций, уравнений, неравенств. 14141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414141414

Задачи с параметрами для учеников массовой школы являются непривычными, а для многих из них сложными. Недостаточно механического применения формул, необходимо понимание закономерностей, навыки анализа конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат. Часто изобилие всевозможных вариантов и подвариантов, на которые распадается основной ход решения, вызывают трудности в выписывании ответа. Решение задач с параметрами требует исследования, даже если это слово не упомянуто в формулировке задачи. Этим обусловлены трудности, возникающие у учащихся при решении таких задач,

В последние годы задачи с параметрами (и прежде всего уравнения и неравенства с одним параметром) постоянно встречаются на вступительных экзаменах в высшие учебные заведения. Таким образом, очевидна необходимость отработки приемов решения различных задач с параметрами. К сожалению, программа не дает ответа на вопрос, в какое время и как школьник должен осваивать решение задач с параметрами.

Цель настоящей работы состоит в том, чтобы рассмотреть возможности введения понятия «параметр» с 7 – го класса, не выходя за рамки программы.

Впервые знакомиться с параметрами полезно в 7-м классе при изучении линейных уравнений, чтобы ученики привыкли к понятию «параметр» и не испытывали затруднений при изучении этой темы в старших классах. Кроме того, задачи с параметрами хорошо развивают логическое мышление, тренируют внимание и память.

Прежде чем ввести понятие «параметр» ученикам необходимо напомнить роль буквы в алгебре и предложить задания в которых надо выразить одну переменную через другую.

Выразите х через другие переменные:

а) ; б) ; в)

г) ; д)

Семиклассники хорошо решают линейные уравнения с параметрами.

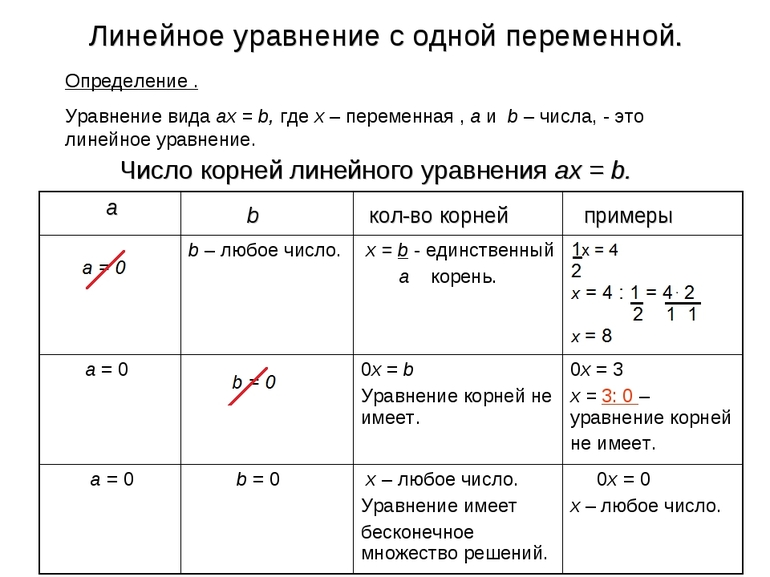
Вспомним, что называется линейным уравнение с одной переменной.

Определение: Уравнение вида ax = b , где х – переменная, a и b – некоторые числа, называется линейным уравнением с одной переменной.

Алгоритм решения уравнения ax = b .

1) если а  0, то ;

2) если а = 0, b  0, то корней нет (0 x = b )

3) если а = 0, то х – любое (0 x = 0)

Повторив на простых примерах, что значит решить уравнение, обратим внимание учащихся на то, что мы выразили неизвестное через числа.

Однако, в уравнении помимо неизвестного могут быть введены другие буквы и буквенные выражения.

При этом, как всегда в алгебре, мы полагаем, что буквы могут принимать любые числовые значения.

Например, задавая произвольно значения а для уравнения ax = a – 1, получим:

Пример 1: Решите уравнение х + 2 = а + 7 относительно х .

Переменную, которую надо найти, будем называть неизвестной, а переменную, через которую будем выражать искомую неизвестную, назовем параметром.

Решить уравнение с параметром – это значит для каждого значения параметра найти значение неизвестной переменной, удовлетворяющее этому уравнению.

Значение х находится по формуле х = 5 + а , подставляя в нее задаваемые значения параметра а . Заметим, что значения параметра а задаем произвольно.

В нашем примере: при а = 3 х = 8; при а = 0 х = 5; при а = –4 х = 1.

Ответ запишем так: при любом значении параметра а х = 5 + а.

Когда начинать решать такие уравнения? В зависимости от уровня класса, на уроках в течение всего года. Параллельно решаем задачу, обратную данной.

Пример 2: При каком значении параметра а х = 2,5 является корнем уравнения х + 2 = а + 7?

Решение: Т.к. х = 2,5 корень уравнения х + 2 = а + 7, то при подстановке х = 2,5 в уравнение получим верное равенство: 2,5 + 2 = а + 7

Ответ: при а = – 2,5.

Можно предложить ученикам придумать линейное уравнение с параметром и решить его.

Пример 3: Решите уравнение ах = 1

В 7 классе начинаем обращать внимание учеников на запись ответа.

В нашем примере можно записать следующим образом

Ответ: если а = 0, то корней нет, если а  0, то .

Пример 4: Решите уравнение ах + 8 = а ( а – параметр)

Ответ: при а = 0 – нет корней, при а  0 .

Пример 5: Решите уравнение ( а – 1) х = 12

Ответ: если а = 1, то корней нет, если а  1, то .

Пример 6: Решите уравнение х ( а + 2) – а (1 – х ) = 3

ах + 2 х – а – ах = 3; 2 ах + 2 х – 3 = а; 2 х ( а + 1) – 3 = а;

Ответ: если а = – 1, то корней нет,

если а  – 1, то .

Самостоятельная работа (обучающая)

1) Найдите значение а , при котором число 2 является корнем уравнения х ( а – 2) – а (1 – х ) = 3

Ответ: .

2) Решите уравнения:

а) 2 х – 3( х – а ) = 3 + а; Ответ: х = 2 а – 3

б) ах – 3(1 + х ) = 5; Ответ: если а = 3, то корней нет, если а  3, то .

в) Ответ: если а = 0, то корней нет, если а  0, то .

Далее можно ввести и алгоритм решения уравнений с параметром; продолжить работу по формированию умений решать линейные уравнения с параметром.

Условия для поиска значения параметра а

Характеристика множества корней

1. k ( a ) не имеет смысла

2. b ( a ) не имеет смысла

один корень

Применим этот алгоритм к решению уравнений.

Пример 1: Решите уравнение

Решение: ,

k ( a ) не имеет смысла при а = 2

b ( a ) не имеет смысла при а = – 3

, система решений не имеет

4) , , если а  – 2, а  – 3, а  2, то

5) , система имеет единственное решение при а = – 2.

Ответ: если а = 2, а = – 3, то решений нет; если а  – 2, а  – 3, а  2, то ;

если а = – 2, то х – любое число.

Пример 2: Решите уравнение ( k 2 – 1) x = k + 1

Решение: 1) k + 1 имеет смысл при любом k .

2) k 2 – 1 имеет смысл при любом k .

3) , при k = 1 исходное уравнение решений не имеет

4) ( k 2 – 1)  0, ( k – 1) ( k + 1)  0; если k  1, k  – 1, то

, .

5) , если k = – 1, то х – любое число.

Ответ: если k = 1, то решений нет; если k = – 1, то х – любое число; если k  1, k  – 1, то .

Пример 4: При каких значениях параметров m и n уравнение 2 m – nx = 1 не имеет решений? Ответ: если n = 0 и , то корней нет; если n  0 и m любое число, то ;

если n = 0 и , то х любое число.

Для самостоятельной работы:

а)

б)

Ответ: если а = 0 и b  – 3, то корней нет; если а = 0 и b – любое число, то ;

если а = 0 и b = – 3, то х любое число.

Задания для закрепления:

Ответы: а) х = ; б) х = 3 с; в) х = – (7 b + 6 a ); г) х =

д)При каких значениях уравнение имеет положительное решение?

е) При каких значениях уравнение имеет отрицательное решение?

ж) При каких значениях уравнение имеет одно положительное решение?

з) При каких значениях уравнение имеет решения, удовлетворяющее условию ?

Решение квадратных и дробно-рациональных уравнений, содержащих параметры – один из труднейших разделов школьной математики. Здесь, кроме использования определенных алгоритмов решения уравнений, приходится думать об удачной классификации. Квадратные и дробно-рациональные уравнения с параметрами – это тема, на которой проверяется не натасканность ученика, а подлинное понимание им материала.

Что должны знать восьмиклассники?

Определение: квадратным уравнением называется уравнение вида , где х – переменная, а , b и с – некоторые числа, при чем а ¹ 0.

Определение: если в квадратном уравнении хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением.

Выражение называется дискриминантом квадратного уравнения .

Если D > 0, то уравнение имеет два корня

и .

Если D = 0, то уравнение имеет один корень .

Пример 1: Линейным или квадратным является уравнение относительно х , при : а) b = 1; б) b = 2; в) b = 0,4; г) b = 0?

Решение: а) b = 1; – квадратное уравнение;

б) b = 2;

– линейное уравнение;

в) b = 0,4;

– неполное квадратное уравнение;

г) b = 0;

–линейное уравнение.

Итак, в зависимости от значений параметра b , уравнение может быть квадратным, линейным или неполным квадратным уравнением.

Пример 2: При каких значениях параметра а уравнение является:

а) квадратным; б) неполным квадратным; в) линейным?

а) Уравнение является неполным квадратным, если:

если а Î (– ¥ ; – 2) È (– 2; 0) È (0; 1) È (1; + ¥ ), то исходное уравнение является квадратным.

б) Уравнение является линейным, если при а = 0 или а = 1.

Пример 3: При каких значениях параметра b уравнение

а) имеет корни; б) не имеет корней?

Решение: ; D =

а) , но , следовательно, ;

если , то уравнение корни имеет.

б) – при любых значениях b , кроме нуля;

если b Î (– ¥ ; 0) È (0; + ¥ ), то исходное уравнение корней не имеет.

Для закрепления можно предложить следующие упражнения:

Пример 1: Решите относительно х уравнение

Решение:

Ответ: если а = 0, то х = 0;

Пример 2: Решите относительно х уравнение

Решение: , D = 4 – 4 с

Алгоритм: рассмотреть случаи, когда: D > 0, D = 0, D

3) с > 1 исходное уравнение корней не имеет.

Ответ: если с Î (– ¥ ; 1), то

если с = 1, то х = 1

если с Î (1; + ¥ ), то корней нет.

Пример 3: Решите относительно х уравнение

Решение

В первую очередь, обратить внимание учащихся на коэффициент перед х 2 .

1) если m = 0, то

2) если m ¹ 0, то D = 36 – 4 m

б) 36 – 4 m = 0, m = 9, х =

в) 36 – 4 m 0, m > 9, исходное уравнение корней не имеет.

Ответ: если m Î (– ¥ ; 0) È (0; – 9), то

если m = 0, то х =

если m Î (9; + ¥ ), то корней нет.

Ответы: 4) если с = 2, то y – любое число;

5) если b = 0, то y – любое число;

7) при а = 0 y – любое число;

при а ¹ 0 корней нет.

8. Решите уравнения :

а) ; в)

б) ; г) .

а) ; в)

б) ; г)

а) ; в)

б) ; г) .

Уже в 8 классе можно решать квадратные уравнения, содержащие параметр, с ограничением на корни.

Выделим задачи, в которых благодаря параметрам на переменную накладываются какие-либо искусственные ограничения. Для таких задач характерны следующие формулировки: при каком значении параметра уравнение имеет одно решение, два, бесконечно много, ни одного; уравнение имеет два различных корня, положительные корни и т.д.

Пример 1: При каких а уравнение имеет единственное решение?

Решение: естественно начать решение со случая а = 0. Итак, если а = 0, то очевидно, что данное уравнение имеет единственное решение. Если же а ¹ 0, то имеем дело с квадратным уравнением. Его дискриминант 1 – 2 а принимает значение, равное нулю, при а = .

Ответ: а = 0 или а = .

Пример 2: При каких а уравнение имеет два различных корня?

Решение: данное уравнение является квадратным относительно переменной х при а ¹ 0 и имеет различные корни, когда его дискриминант , т.е. при а а = 0 получается уравнение , имеющее один корень. Таким образом, а Î (– ¥ ; 0) È (0; 1).

Ответ: а Î (– ¥ ; 0) È (0; 1).

Рассмотрим несколько примеров, где значения параметра расставляют «ловушки».

Пример 3: При каких а уравнение имеет более одного корня?

Решение: при а = 0 уравнение имеет единственный корень, что не удовлетворяет условию. При а ¹ 0 исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант – положительный. Отсюда получаем: . Однако в полученный промежуток (– 4; 1) входит число 0, которое, как мы уже проверили, неприемлемо.

Ответ: или .

Пример 4 (для самостоятельного решения): При каких а уравнение имеет более одного корня?

Решение: Стандартный шаг – начать со случаев а = 0 и а = – 3. При а = 0 уравнение имеет единственное решение. Любопытно, что при а = – 3 решением уравнения является любое действительное число. При а ¹ 0 и а ¹ – 3, разделив обе части данного уравнения на а + 3, получим квадратное уравнение , дискриминант которого положителен при а > – .

Опыт решения предыдущего примера подсказывает, что из промежутка ( –; + ¥ ) надо исключить точку а = 0, а в ответ не забыть включить а = – 3.

Ответ: а = – 3, или – а а > 0.

К этой группе задач примыкают задачи , содержащие параметр, решаемые с использованием теоремы Виета.

Теорема Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

D > 0 :

Итак , .

Пример 1: При каких значениях параметра b уравнение имеет:

а) два положительных корня;

б) два отрицательных корня;

в) единственный корень?

если b ¹ 1, то

а) согласно теореме Виета , b Î (– ¥ ; – 1) È ( – 1; + ¥ )

б) , решений нет

в) если b = 1, то –2 х + 2 = 0; х = 1; b ¹ 1; .

Ответ: а) b Î (– ¥ ; – 1) È ( – 1; + ¥ ); б) таких b не существует; в) х = 1.

1.При каких значениях параметра а уравнение имеет:

а) два положительных корня;

б) два отрицательных корня;

в) корни разных знаков?

Ответ: а) а Î (2; + ¥ ); б) а Î (– ¥ ; – 3); в) а Î (– 3; 2).

2. При каких значениях параметра b уравнение имеет:

а) два положительных корня;

б) два отрицательных корня;

в) корни разных знаков?

Ответ: а) b Î (2; + ¥ ); б) b Î (– ¥ ; – 1); в) b Î (– 1; 2).

Пример 2: При каком значении q один корень уравнения равен квадрату второго?

Решение: Если корни уравнения связаны соотношением , то по теореме Виета

Тогда , , ; ; .

5. При каких значениях параметра с уравнение имеет:

а) два положительных корня;

б) два отрицательных корня;

в) единственный корень?

6. При каких значениях параметра с уравнение

б) не имеет корней;

в) имеет положительный корень;

г) имеет отрицательный корень?

Ответы: 1) а) При с > 8; б) при с с = – 8 или с = 8.

2) а) с Î (– ¥ ; –) È (–; + ¥ ); б) с = –); в) с Î (–; + ¥ ); г) с Î (– ¥ ; –).

1. При каких значениях произведение корней квадратного уравнения равно нулю?

2. При каких значениях сумма корней квадратного уравнения равна нулю?

3. В уравнении сумма квадратов корней равна 16. Найти .

4. В уравнении квадрат разности корней равен 16. Найти .

5. При каких значениях сумма корней уравнения равна сумме квадратов корней?

6. При каком значении параметра сумма квадратов корней уравнения наименьшая?

7. При каком значении параметра сумма квадратов корней уравнения наибольшая?

8. При каких значениях параметра один из корней квадратного уравнения в два раза больше другого?

9 .При каких значениях уравнение имеет корни разных знаков?

10. При каких значениях уравнение имеет корни и такие, что ?

Тест состоит из 5-ти заданий, последнее из них более сложное. Для каждого задания предлагается три ответа, один из которых правильный, а два другие – неверные. Класс делится на 2 варианта. Каждому ученику дается карточка с заданиями соответствующего варианта.

Вариант 1

1. Решите уравнение относительно х.

а) , при m ¹ 0.

б) 1) при m = 0 корней нет;

2) при m ¹ 0 ;

в) 1) при m = 0 корней нет;

2) при m ¹ 0 .

2. Решите уравнение относительно х.

а) 1) при ;

2) при корней нет;

3) при

б) 1) при ;

2) при корней нет;

3) при

в) 1) при ;

2) при корней нет;

3) при ;

4) при

3. При каких значениях b уравнение имеет отрицательное решение?

4. При каких значениях а произведение корней уравнения равно нулю?

а) при ; б) при ; в) при .

5. При каком значении b сумма квадратов корней уравнения принимает наименьшее значение?

а) таких значений нет; б) при ; в) при .

Уравнения с параметром — алгоритмы и примеры решения

Общие сведения

Уравнением является любое математическое тождество или физический закон, в котором присутствуют неизвестные величины. Последние необходимо находить. Этот процесс называется поиском корней. Однако не во всех случаях у равенства с переменными бывают решения, а это также нужно доказать.

Корень — величина или диапазон, превращающие искомое выражение в верное равенство. Например, в 5s=10 переменная эквивалентна 2, поскольку только это значение позволяет получить верное тождество, то есть 5*2=10.

Примером диапазона или интервала решений является выражение следующего вида: 0/t=0. Его корнем может быть любое действительное число, кроме нуля. Записывается решение в таком виде: t ∈ (-inf;0)U (0;+inf), где «∈» — знак принадлежности, «-inf» и «inf» — минус и плюс бесконечно большие числа соответственно.

Параметром в уравнении называется некоторая величина, от которой зависит поведение равенства на определенном интервале. Следует отметить, что он также влияет на значение корня, когда входит с ним в различные арифметические операции: сложения, вычитания, умножения, деления, возведения в степень и так далее. Тождества такого типа называют также параметрическими. Далее необходимо разобрать классификацию уравнений.

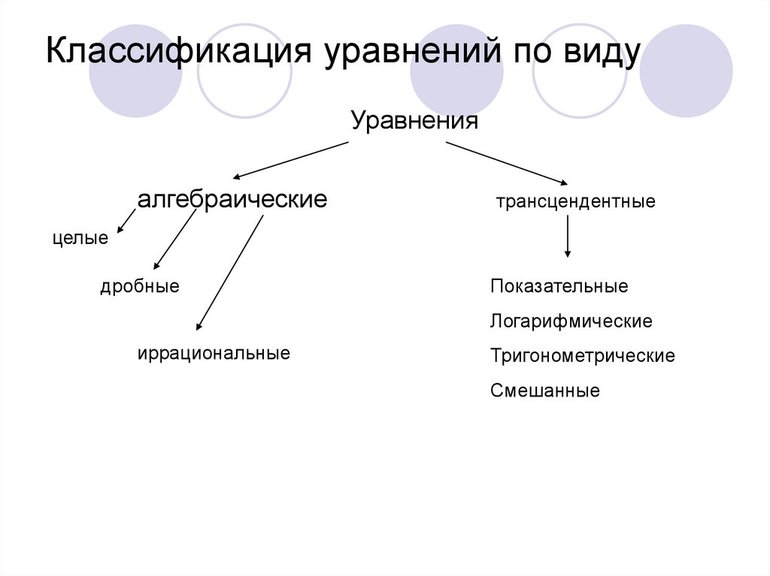
Классификация уравнений

Уравнения делятся на определенные виды, от которых зависит выбор методики их решения. Они бывают следующими: алгебраическими, дифференциальными, функциональными, трансцендентными и тригонометрическими. Кроме того, все они могут содержать некоторую величину — параметр. Его часто обозначают литерой «р» или «а».

Алгебраический тип является наиболее простым, поскольку не содержит сложные элементы. Дифференциальные тождества с неизвестными — одни из самых сложных выражений с точки зрения алгоритма. Они бывают первого, второго, третьего, а также высших порядков. Для нахождения их корней необходимо знать правила дифференцирования и интегрирования.

Практически все функциональные уравнения содержат один или более параметров. Основное их отличие от остальных заключается в функции, которая задается сложным выражением. Последнее может включать несколько неизвестных и параметрических элементов. Примером такого тождества является функция Лапласа, содержащая интеграл обыкновенного типа, а также экспоненту.

К трансцендентным относятся выражения, содержащие показательную, логарифмическую и радикальную (знак корня). Последний тип — тригонометрические. Они содержат любое равенство, содержащее следующие функции: sin, cos, tg и ctg. Однако в математике встречаются также их производные: arcsin, arccos, arcctg, arctg и гиперболические тождества.

Специалисты рекомендуют освоить на начальных этапах обучения методики, позволяющие решать уравнения с параметром линейного типа. После этого можно переходить к более сложным тождествам — функциональным, трансцендентным и так далее.

Алгебраический вид

Алгебраические не содержат в своем составе сложных функций, но в них могут присутствовать компоненты со степенным показателем.

На основании последней характеристики они делятся на 5 типов:

Линейные.
Квадратные (квадратичные).
Кубические.
Биквадратные.
Высших порядков.

Линейные — выражения с переменной, которая имеет только первую степень (равную единице). Если показатель эквивалентен двойке, то такое тождество называется квадратным. В математической интерпретации его еще называют квадратным трехчленом. Когда показатель при неизвестной эквивалентен тройке, тогда это равенство называется кубическим.

Наиболее сложными по своей структуре являются биквадратные (содержат 4 степень). Однако на этом виды линейных уравнений не заканчиваются, поскольку бывают равенства с более высокими показателями. Их называют уравнениями высших порядков. Кроме того, любые тождества могут объединяться в системы уравнений. Их особенностью являются общие решения.

Линейные и квадратичные

Линейное — это самое простое уравнение, которое имеет всего одно решение. Оно решается по следующей методике:

Записывается искомое выражение.
При необходимости раскрываются скобки и приводятся подобные элементы.
Неизвестные (переменные) остаются в левой части тождества, а все константы (числа) — переносятся вправо.
Правая часть сокращается на коэффициент при неизвестной.
Записывается результат.
Выполняется проверка посредством подстановки корня в исходное выражение.

Следует отметить, что линейное выражение с переменной может не иметь решений, поскольку иногда невозможно выполнить операцию сокращения. Например, 0t=85. Равенство не имеет корней, поскольку на нулевое значение делить нельзя, так как при этом получается пустое множество.

Следующим типом является уравнение квадратичной формы At 2 +Bt+C=0. Оно может иметь один или два решения. Однако бывают случаи, при которых корней нет вообще. Для получения результата вводится понятие дискриминанта «D=(-B)^2−4*А*С». Для решения следует воспользоваться следующим алгоритмом:

Записать выражение.
Выполнить при необходимости математические преобразования по раскрытию скобок и приведению подобных слагаемых.
Вычислить значение D (D 0 — два решения).
При D=0 формула корня имеет такой вид: t=-В/(2А).
Если D>0, то решения определяются по следующим соотношениям: t1=[-В-D^(½)]/(2А) и t2=[-В+D^(½)]/(2А).
Записать результат.
Выполнить проверку по отсеиванию ложных корней.

Следует отметить, что ложный корень — значение переменной, полученное по соответствующей формуле, но при подстановке в исходное выражение не выполняет условие равенства нулевому значению.

Кроме того, нужно обратить внимание на типы квадратных уравнений. Они бывают полными и неполными. Первые содержат все коэффициенты (А, В и С), а во вторых — некоторые из них могут отсутствовать, кроме А, так как тогда тождество должно содержать вторую степень при неизвестной.

Неполные решаются методом разложения на множители. Например, «v 2 −81=0» раскладывается следующим образом (формула сокращенного умножения — разность квадратов): (v-9)(t+9)=0. Анализируя последнее равенство, можно сделать вывод о понижении степени. Корнями уравнения являются два значения, t1=-9 и t2=9.

Кубичеcкие и биквадрaтные

Кубические и биквадратные равенства с неизвестным рекомендуется решать при помощи замены переменной. Однако в некоторых случаях можно применить формулы понижения степени или разложения на множители. Иными словами, суть решения алгебраических уравнений, степень которых превышает двойку, сводится к ее понижению различными методами.

Замена переменной производится на другую неизвестную величину. В примере (t 3 −2)+2t 3 −4=0 можно ввести следующий элемент — v=t 3 −2. В результате этого получится равенство такого вида: v+2v=0. Оно решается очень просто:

Приводятся подобные элементы: 3v=0.
Находится корень: v=0.
Приравнивается к выражению, которое заменяли: t 3 −2=0.
Находится корень (один, поскольку у радикала нечетная степень): t=[2]^(1/3).
Проверяется условие: 2^(1/3)^3−2+2*(2^(1/3)^3)-4=4−4=0 (истина).

Биквадратные тождества решаются таким же методом. Однако существует еще один способ — разложение на множители. Его необходимо разобрать на примере решения выражения «4m 4 −324=0». Решать нужно по такому алгоритму:

Упростить (вынести четверку за скобки и сократить на нее): 4 (m 4 −81)=m 4 −81=0.
Разложить на множители (разность квадратов): (m 2 −9)(m 2 +9)=(m-3)(m+3)(m 2 +9)=0/
Решить три уравнения: m1=3, m2=-3, m3=-3 и m4=3.
Результат: m1=-3 и m2=3.
Проверка: 4*(-3)^4−324=0 (истинно) и 4*(3)^4−324=0 (истинно).

Каждый из методов решения выбирается в зависимости от самого уравнения. При чтении условия задачи необходимо определить способ решения. Последний должен быть простым и удобным, а главное — количество шагов решения должно быть минимальным, что существенно сказывается на затраченном времени при вычислениях. Далее нужно рассмотреть подробный алгоритм решения уравнения с параметром.

Пример решения

На основании изученного материала можно приступить к практике решения уравнения с параметром, которое имеет следующий вид: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4, где р — некоторый параметр. Корни и величину р необходимо искать по следующему алгоритму:

Записать равенство с неизвестным и параметром: 2v 4 −32−4p-(v 2 +4)+(v-2)(v+2)-v 4 +16=-4.
Выполнить математические преобразования: 2v 4 −32−4p-v 2 +4+v 2 −4-v 4 +16+4=v 4 −16+4p+4=0.
Ввести замену v 4 −16=m: m+4p+4=0.
Вывести формулу нахождения параметра: р=-(m/4)-1.
Подставить величину m: р=-1-(v 4 +16)/4.
C учетом соотношения равенство будет иметь такой вид: v 4 −16+4[-(v 4 +16−4)/4]+4=-32+8=0 (корней нет, поскольку -24 4 −12=0.
Корни: v1=[12]^(¼) и v2=-[12]^(¼).
Отрицательного корня v2 не существует, поскольку показатель радикала — четное число.
Результат: v1=[12]^(¼).
Проверка: <[12]^(¼)>^4−16+4=16−16=0 (истина).

Следует отметить, что v2 — ложный корень, а также параметр p, равный какому-либо значению, превращает уравнение в пустое множество. Для проверки можно воспользоваться специальным приложением, которое называется онлайн-калькулятором.

Таким образом, уравнения с параметром являются наиболее сложными, поскольку необходимо искать их корни, а также некоторое значение, влияющее на логику выражения. Для их решения необходимо следовать специальному алгоритму, предложенному математиками.

источники:

http://infourok.ru/zadachi-s-parametrami-v-kurse-osnovnoy-shkoli-2094471.html

http://nauka.club/matematika/algebra/uravneniya-s-parametrom.html