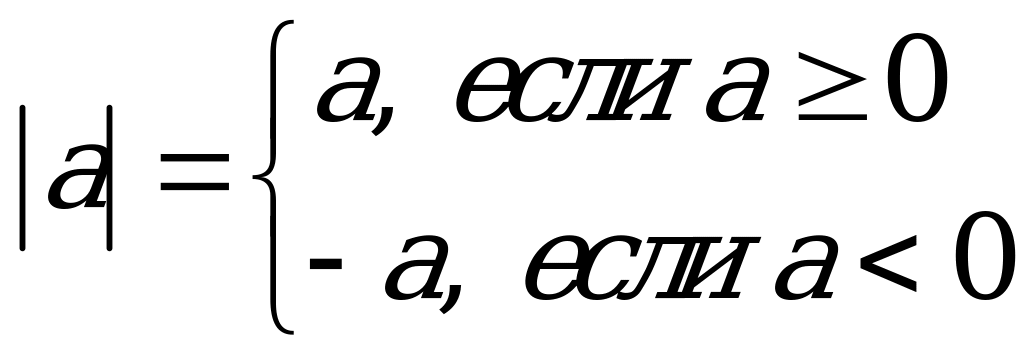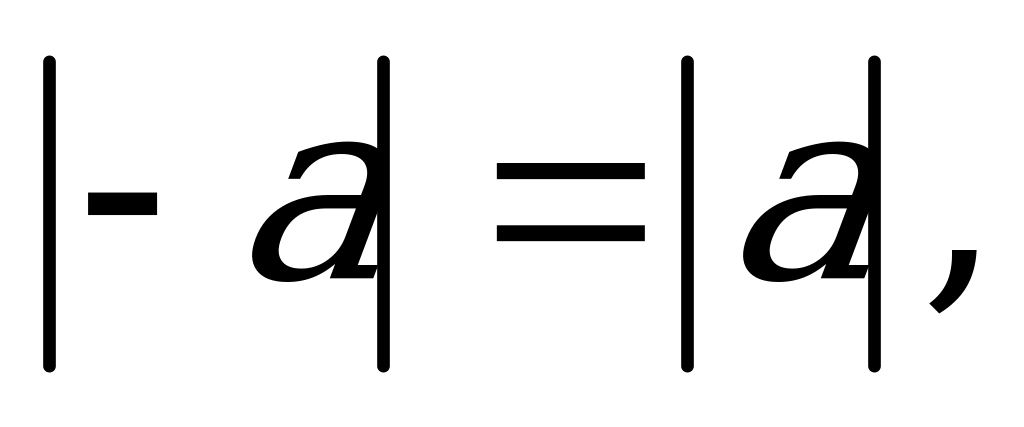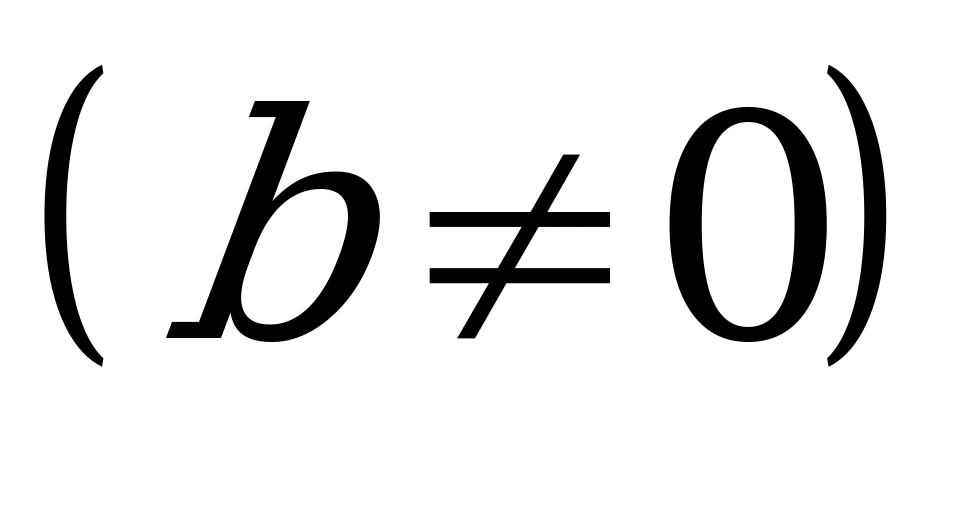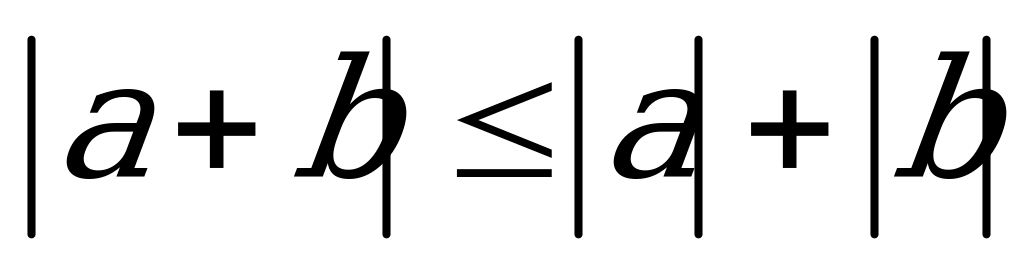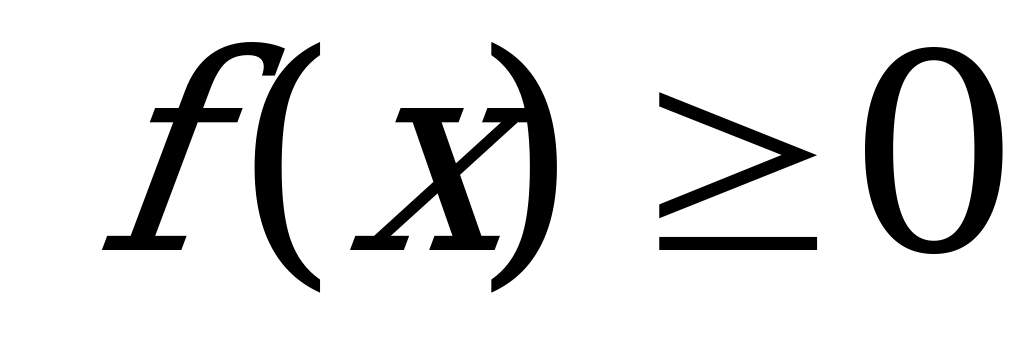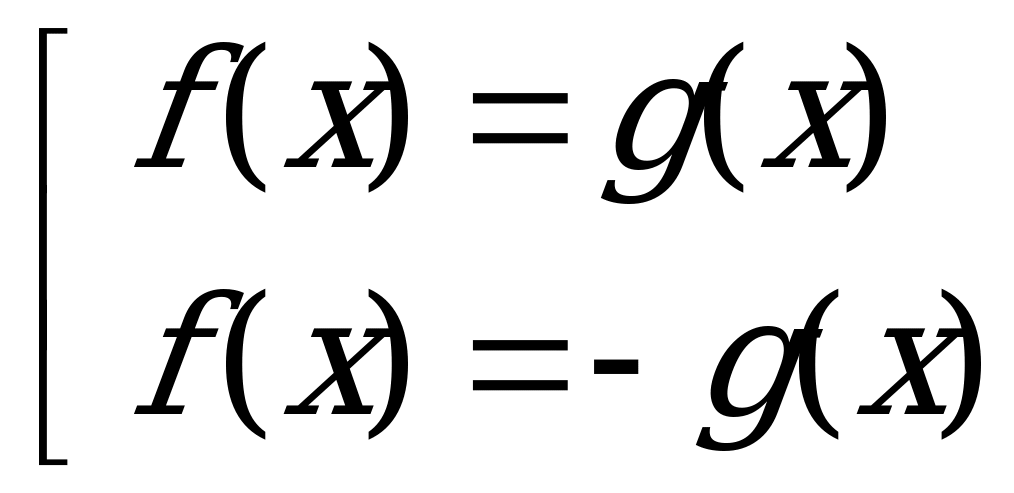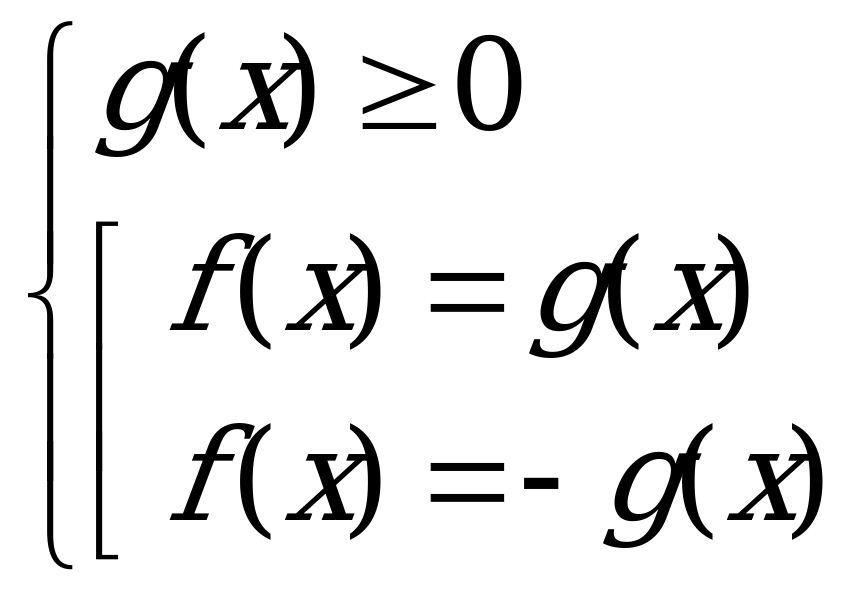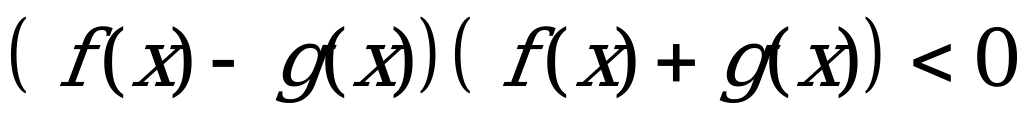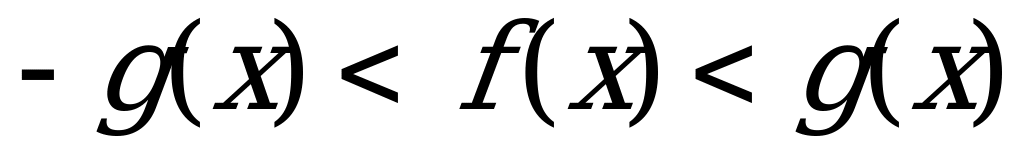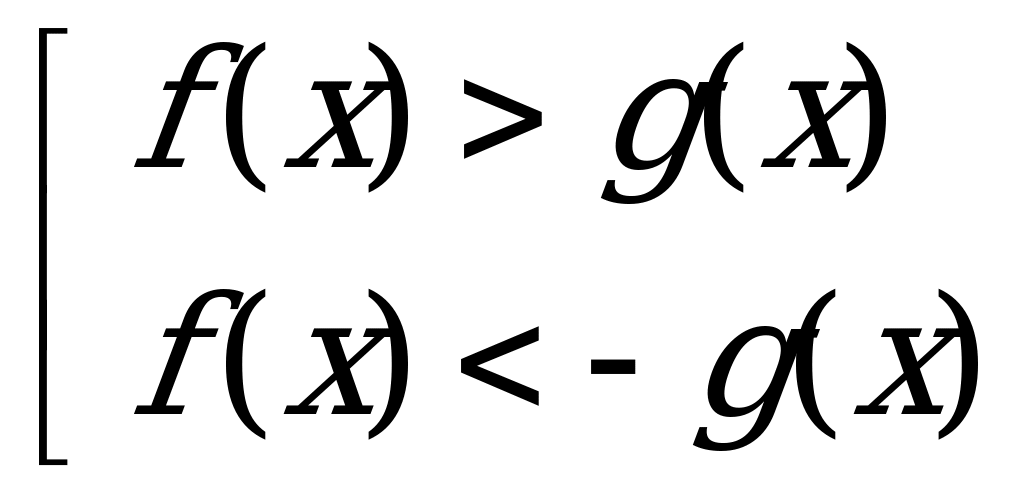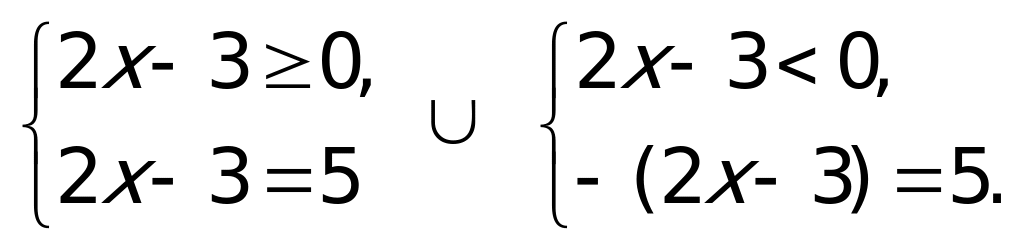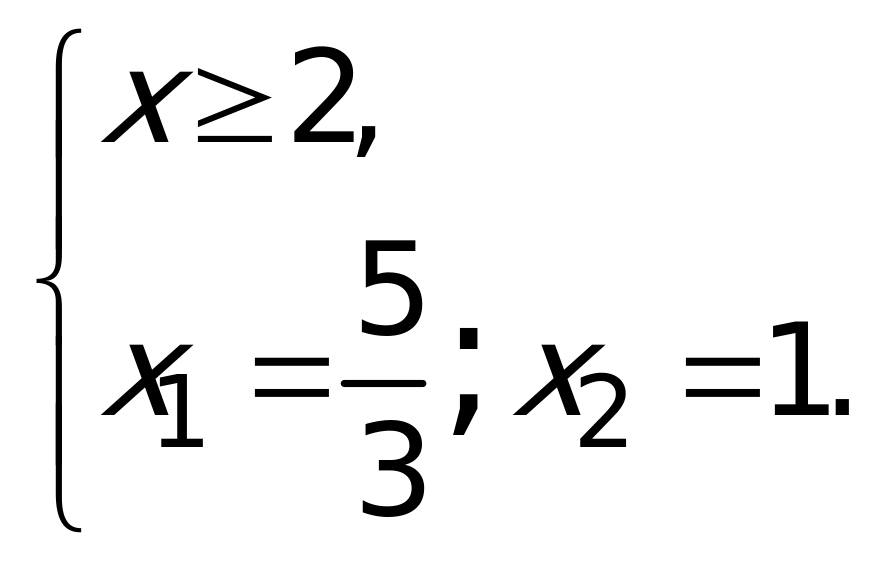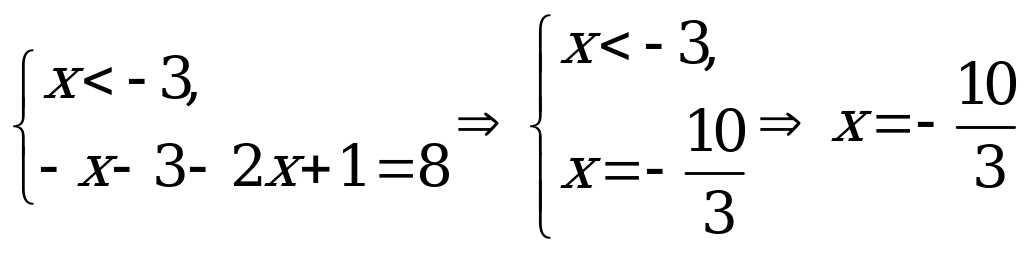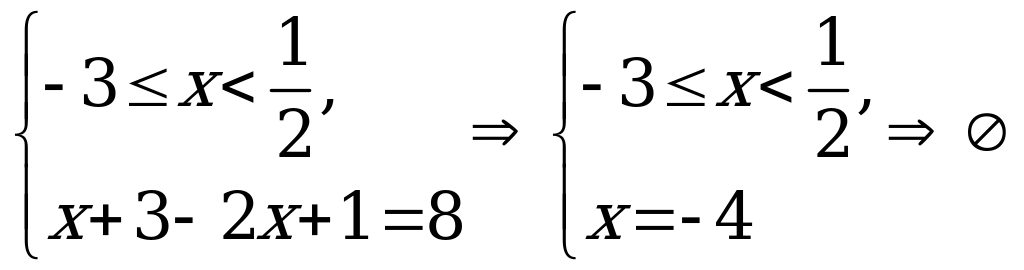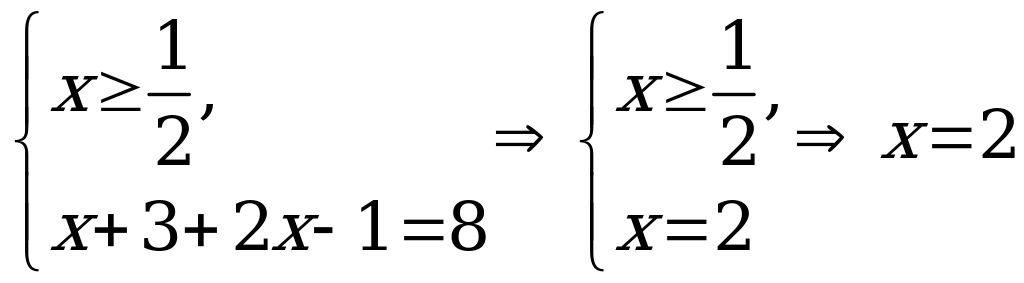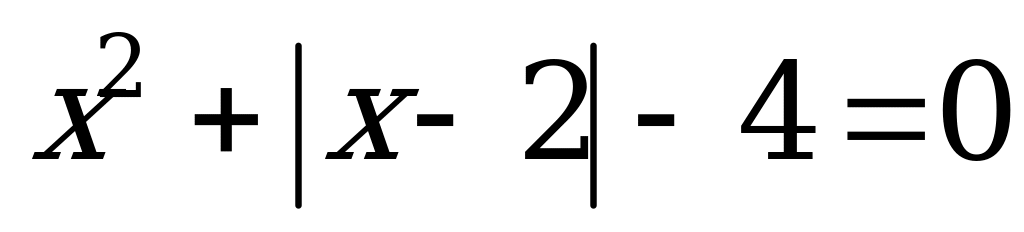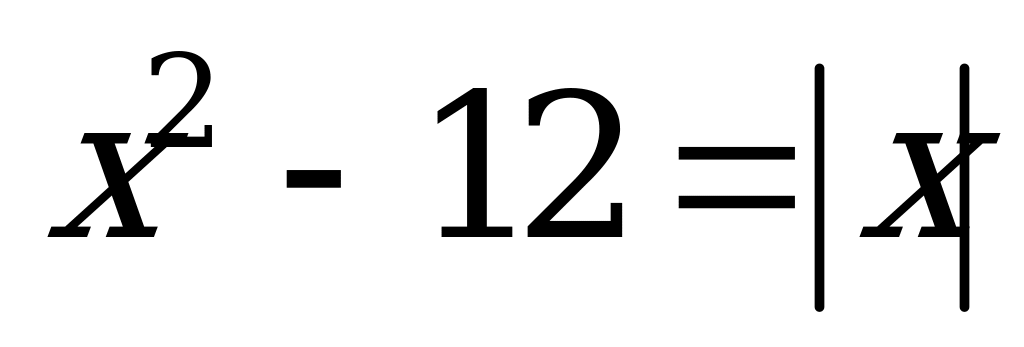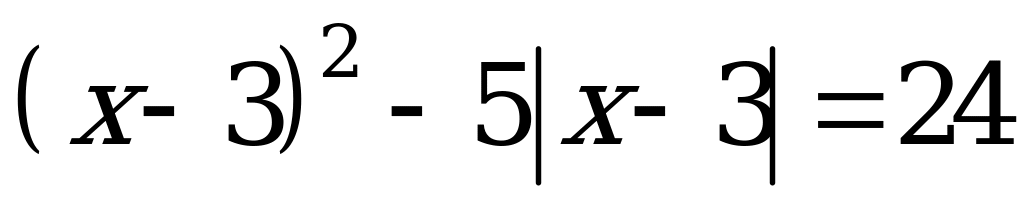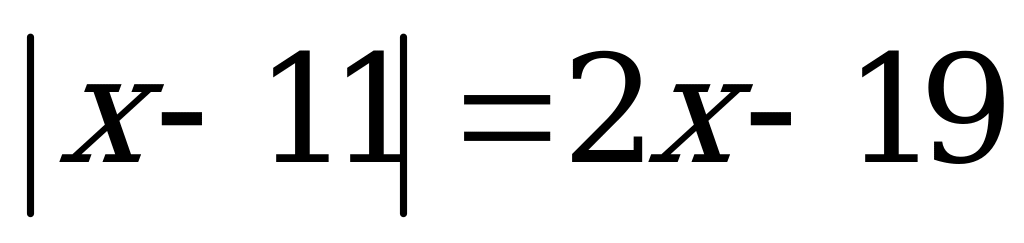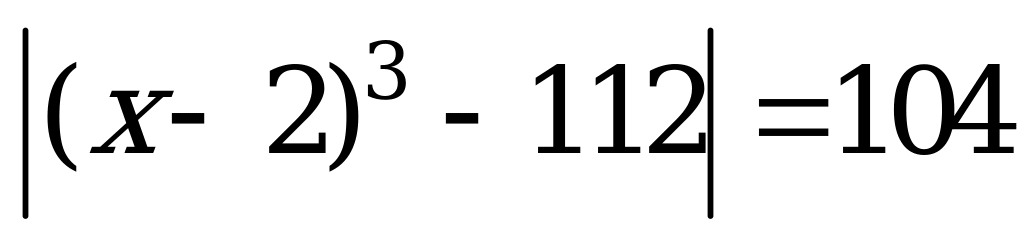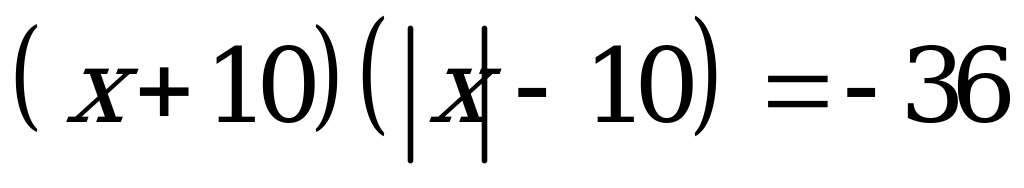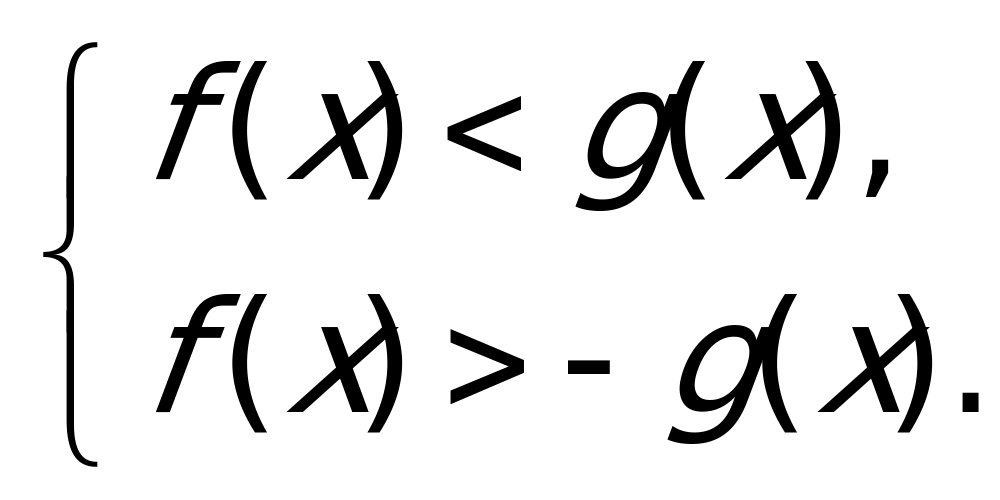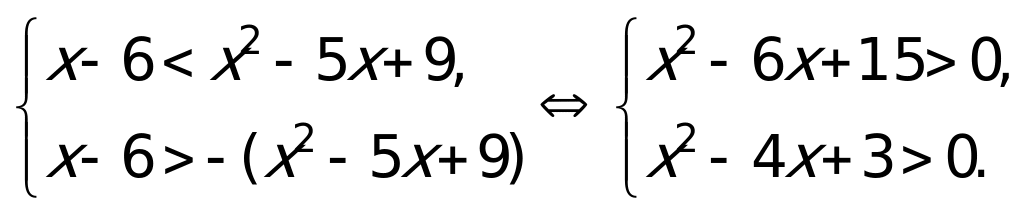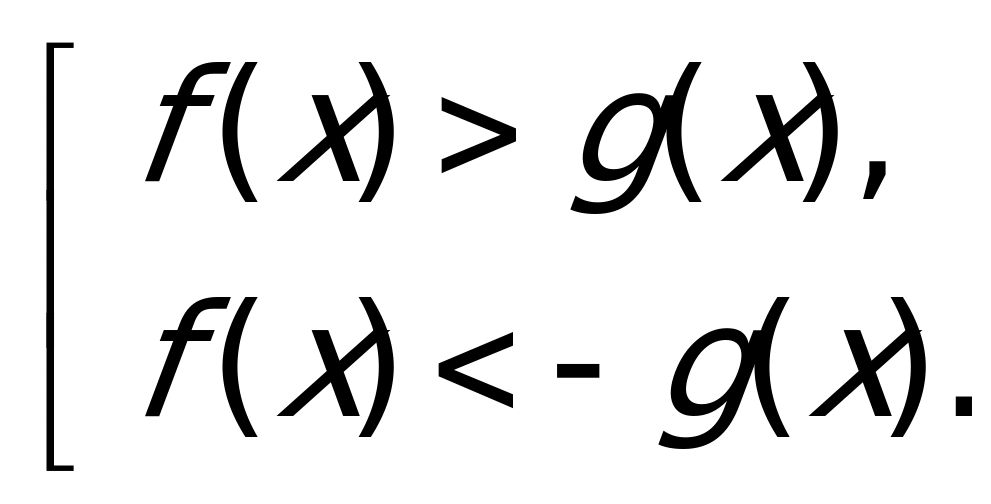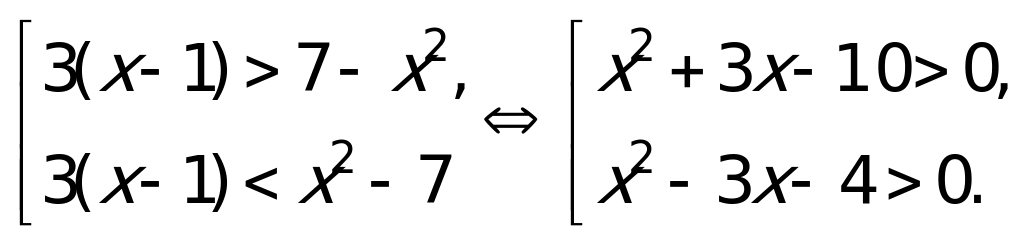Исследовательская работа по математике на тему: «Способы решения линейных уравнений, содержащих знак модуля».
Понятие «модуль» широко применяется во многих разделах школьного курса математики, например, в изучении абсолютной и относительной погрешностей приближенного числа; в геометрии и физике будут изучаться понятия вектора и его длины (модуля вектора). Понятия модуля применяется в курсах высшей математики, физики и технических наук, изучаемых в высших учебных заведениях. Несмотря на то, что тема «Модуль числа» проходит «красной нитью» через весь курс школьной и высшей математики, для ее изучения по программе отводится очень мало времени (в 6 классе -2 часа, в 8 классе — 4 часа).
Исходя из всего вышесказанного, возникает проблема: найти разнообразные методы в обучении решению задач с модулем.
Практически у каждого обучающегося вызывают затруднения задания, содержащие модуль. Это один из самых трудных материалов, с которыми школьники сталкиваются на экзаменах (в заданиях ЕГЭ это задания С5 и С6).
Считаю, что эта тема требует более глубокого исследования, так как она прослеживается в различных заданиях повышенной сложности, которые предлагают учащимся авторы дидактических материалов, в задачах математических олимпиад, в заданиях вступительных экзаменов в Высшие Учебные Заведения и на ЕГЭ.
Указанные обстоятельства обусловили мой выбор темы исследовательской работы.
Основной целью работы считаю получение расширенной информации о модуле числа, его применении, а также о различных способах решения уравнений, содержащих знак абсолютной величины.
Цель исследовательской работы определяет следующие задачи:
— показать необходимость более глубокого рассмотрения темы «Решение линейных уравнений, содержащих знак модуля» в школьной программе;
— разработать алгебраический метод решения линейных уравнений, содержащих знак модуля;
— разработать графический методы решения линейных уравнений, содержащих знак модуля.
Я предположила, что в результате исследования я смогу показать своим одноклассникам и друзьям, что решение уравнений с модулями не являются одним из сложнейших заданий.
Формулирование цели исследовательской работы определяет:
объект исследования – решение уравнений, содержащих знак абсолютной величины;
предмет исследования – алгебраический и графический методы решения линейных уравнений, содержащих знак модуля.
Проектная работа 9 класс «Решение уравнений и неравенств, содержащих переменную под знаком модуля»
Решение уравнений и неравенств, содержащих переменную под знаком модуля, — прекрасный способ с пользой провести свободное время, тренируя при этом свою логику и математическую интуицию.
Просмотр содержимого документа
«Проектная работа 9 класс «Решение уравнений и неравенств, содержащих переменную под знаком модуля»»
Федеральное государственное казённое общеобразовательное учреждение
«Омский кадетский военный корпус
Министерства обороны Российской Федерации»
Проектная (исследовательская) работа
Решение уравнений и неравенств,
содержащих переменную
под знаком модуля
Автор: Чугунов Максим, обучающийся 9-2 класса
1. Модуль: определения, свойства. 4
1. 1. История понятия «модуль» 5
1. 2. Основные равносильные преобразования 5
2. Методы решения уравнений и неравенств, содержащих переменную под знаком модуля 6
2.1. Уравнения с модулем 7
2.2. Неравенства с модулем 13
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость
и упорство в достижении цели.
Решение уравнений и неравенств, содержащих переменную под знаком модуля, — прекрасный способ с пользой провести свободное время, тренируя при этом свою логику и математическую интуицию. К сожалению, данный вид математических задач входит в школьную программу в очень «урезанном» формате – в 8 классе на изучение темы «Модуль числа. Уравнения и неравенства, содержащие модуль» отводится по программе всего 3 урока. Для проекта я выбрал тему «Решение уравнений и неравенств, содержащих переменную под знаком модуля» потому, что посчитал ее очень интересной и актуальной для себя. При подготовке ко второй части ОГЭ по математике мне неоднократно встречались задания с модулями. Заданий в учебнике по данной теме немного, поэтому я планировал также дополнить дидактическую копилку учителя материалом результатами своего проекта и создать интерактивную игру для ребят своей роты, чтобы провести ее на неделе ОД «Математика, информатика и ИКТ».
Нами были определены
Объектная область исследования — учебный предмет «математика».
Объект исследования – решение уравнений и неравенств, содержащих переменную под знаком модуля.
Предмет исследования – математические задачи определенного типа.
— Повторение, обобщение и систематизация имеющихся знаний по теме «Модуль числа»;
— Расширение и углубление знаний по теме «Решение уравнений и неравенств», выработка навыка решения различных уравнений и неравенств, содержащих переменную под знаком модуля;
— Формирование устойчивого интереса к математике, умения и навыков исследовательской, проектной деятельности; развитие навыков самостоятельного поиска информации, формирование умения отбирать и структурировать материал.
Изучить литературу по теме проекта;
Систематизировать все собранные материалы;
Подготовить подборку задач по теме проекта и представить полученные результаты в виде интерактивной интеллектуально-познавательной игры;
Подготовить мультимедийную презентацию для представления результатов работы над проектом.
по виду деятельности – практико-ориентированный;
по организационной форме – индивидуальный;
по времени выполнения — долговременный.
Этапы работы над проектом
Разработанный нами проект включает два этапа:
1-й этап аналитический
2-й этап обобщения
Основные виды работы над проектом:
Изучение дополнительной литературы (справочники, словари, энциклопедии, задачники по математике, Интернет-ресурсы).
Анализ полученной информации (обобщение, сравнение, сопоставление с имеющимися знаниями по данной теме, решение задач).
Модуль: определение, свойства.
Определение (алгебраическое). Модулем (абсолютной величиной) действительного числа а называется число
Кроме того, иногда удобно так называемое геометрическое определение модуля:
Модулем числа называется расстояние от точки, соответствующей этому числу на числовой прямой, до начала координат.
Для любых действительных чисел a, b справедливы соотношения:
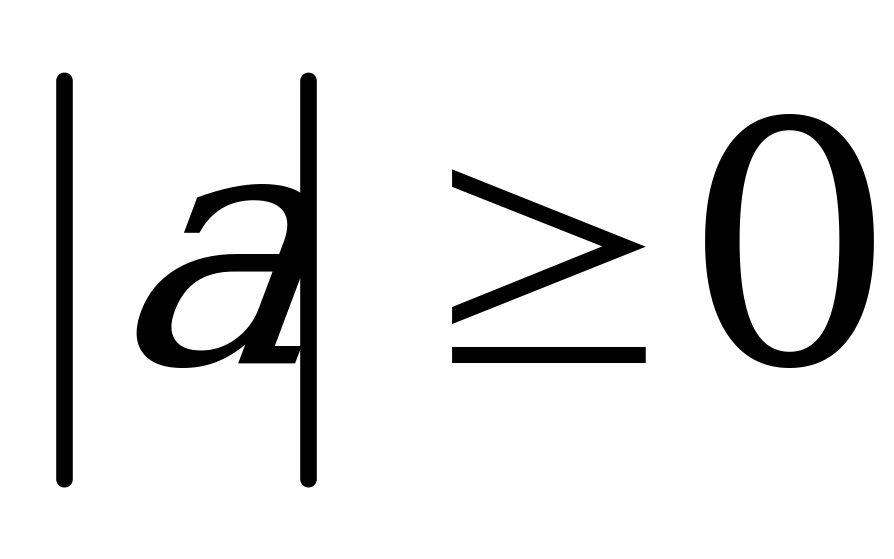
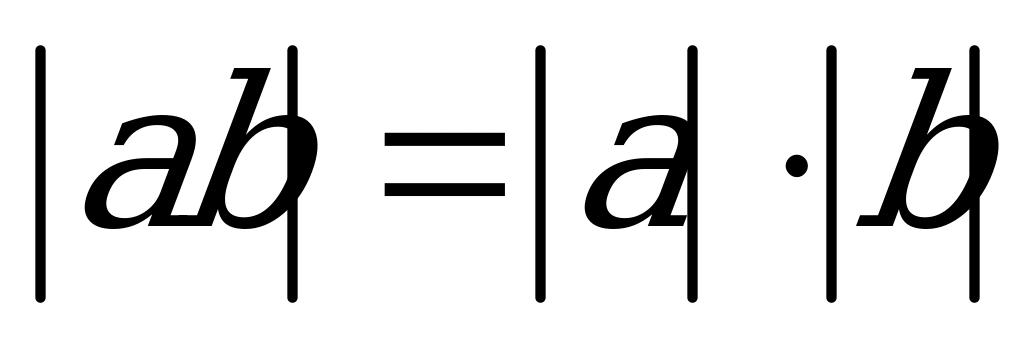
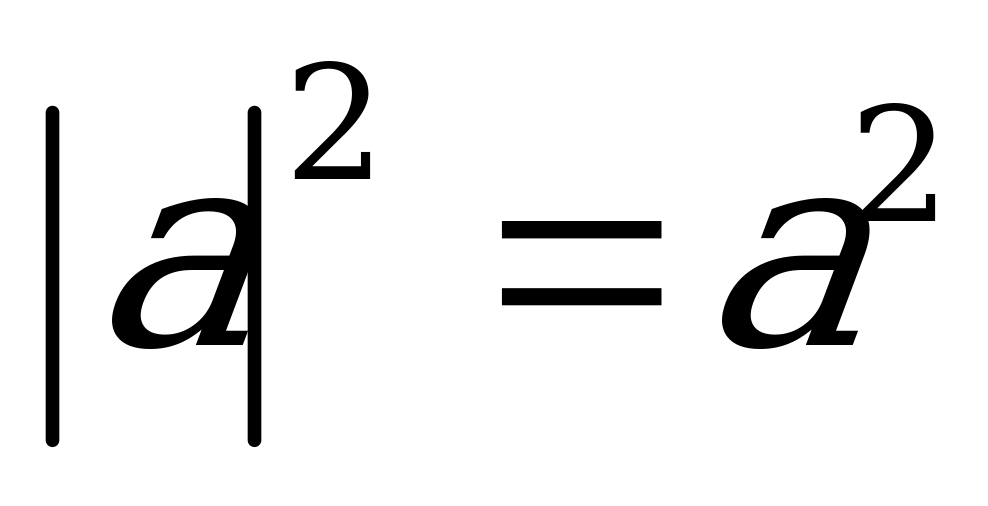
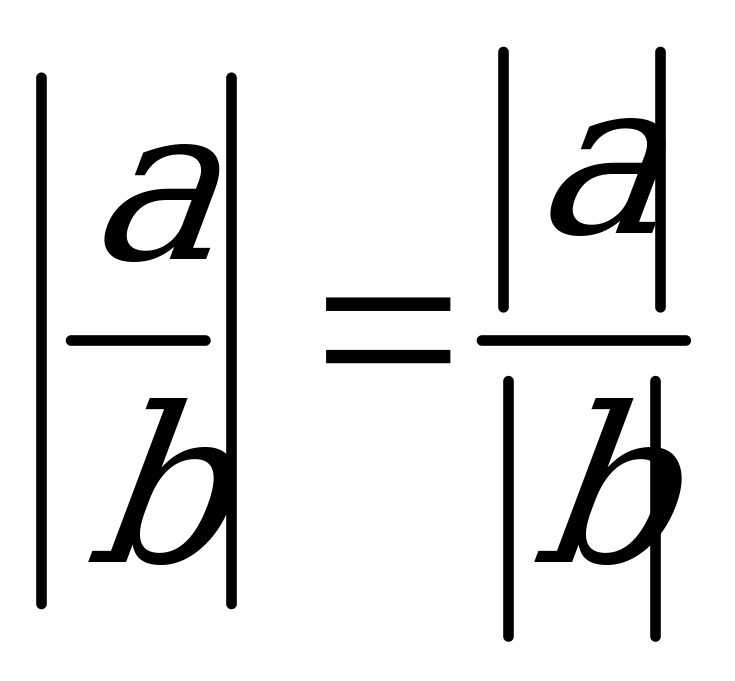
Абсолютная величина (модуль) ( 
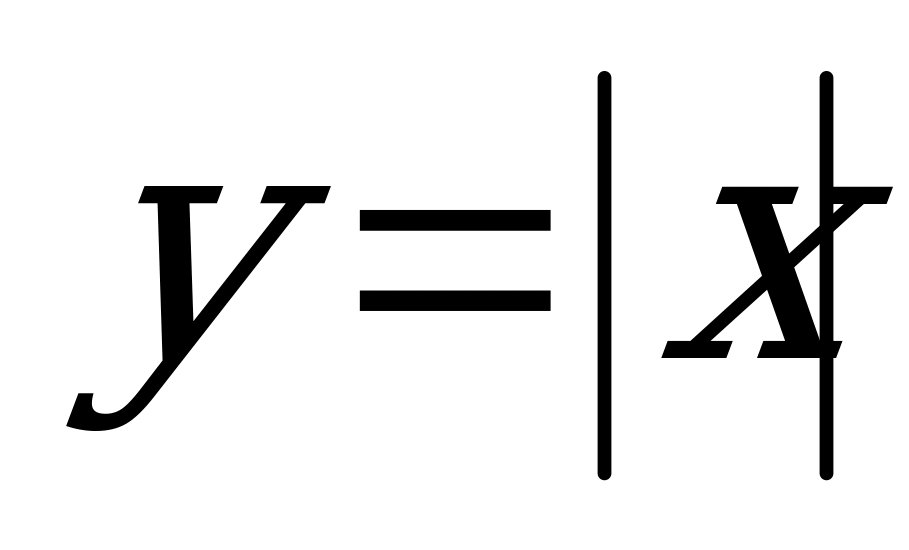
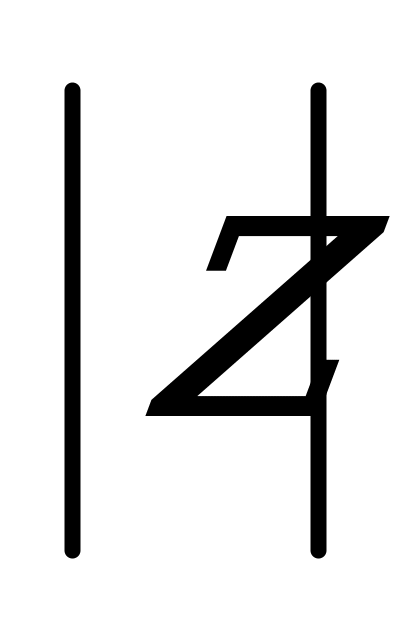
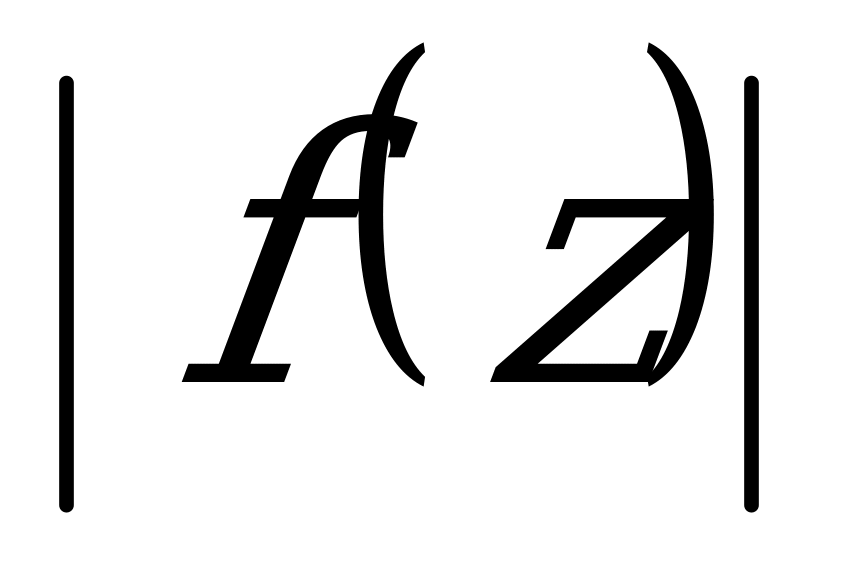
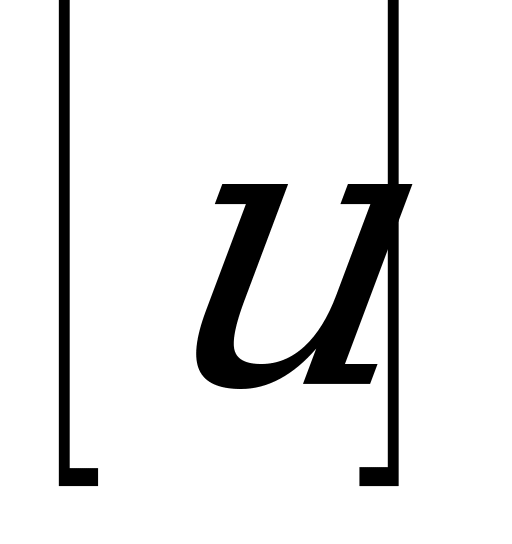

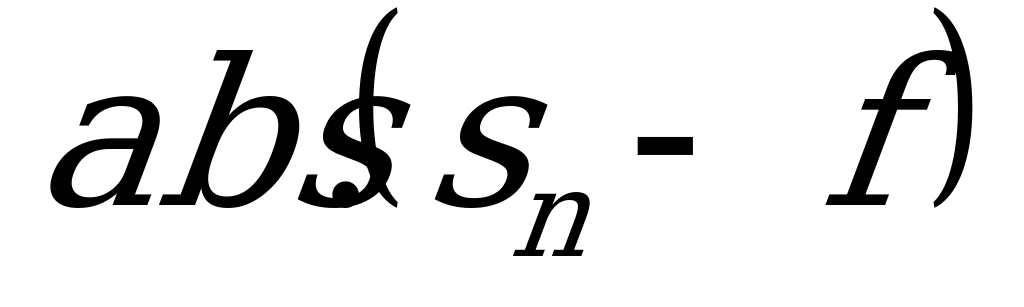
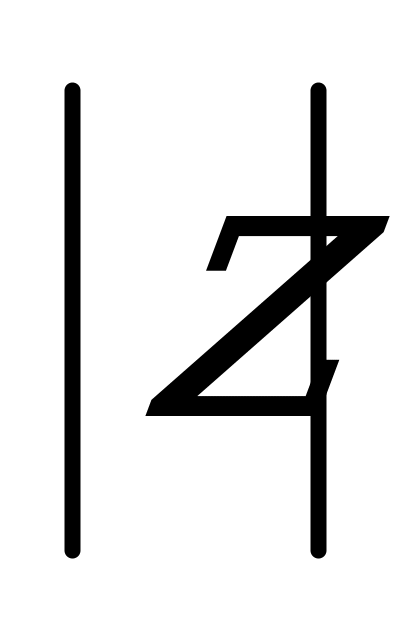
Рассмотрим основные равносильные преобразования, используемые для решения уравнений и неравенств, содержащих переменную под знаком модуля:
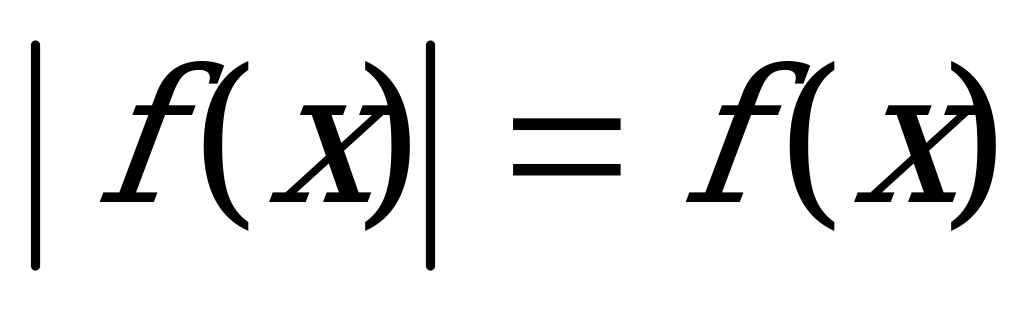

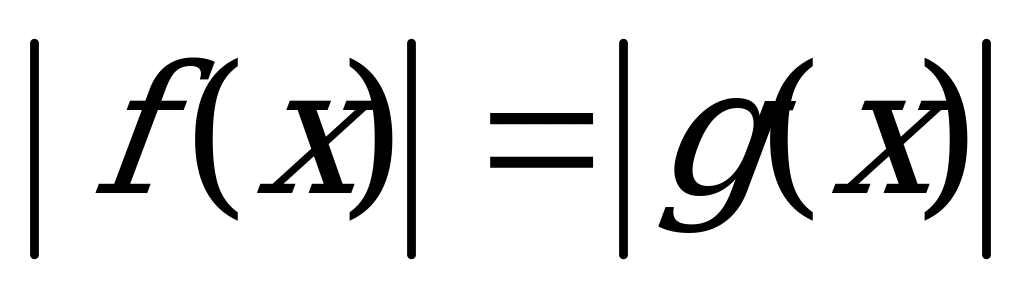

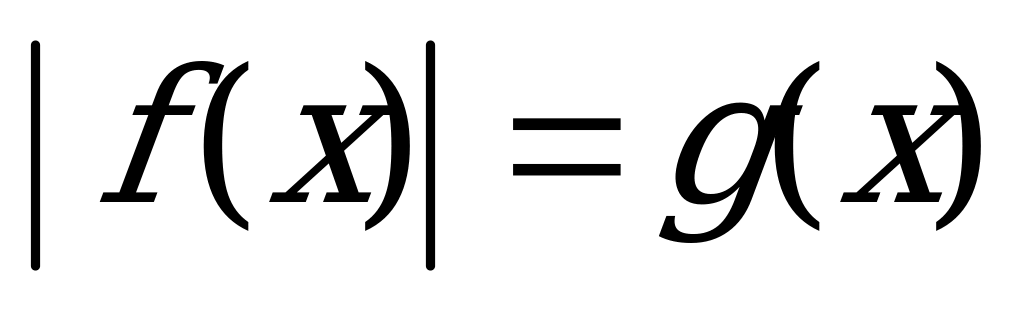

4) Уравнения, представляющие собой алгебраическую сумму двух и более модулей, решаются методом разбиения на промежутки (методом интервалов). На практике это делается так:
находят значения х, при которых выражения, стоящие под знаком модуля, обращаются в ноль;
разбивают область допустимых значений х на промежутки, на каждом из которых выражения под знаком модуля сохраняют знак;
раскрывают все модули на каждом из найденных промежутков и решают полученные уравнения.
Объединение найденных решений составляет множество решений заданного уравнения.
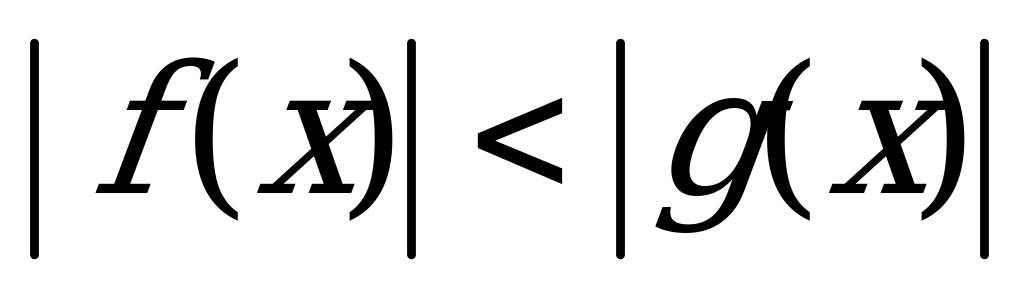

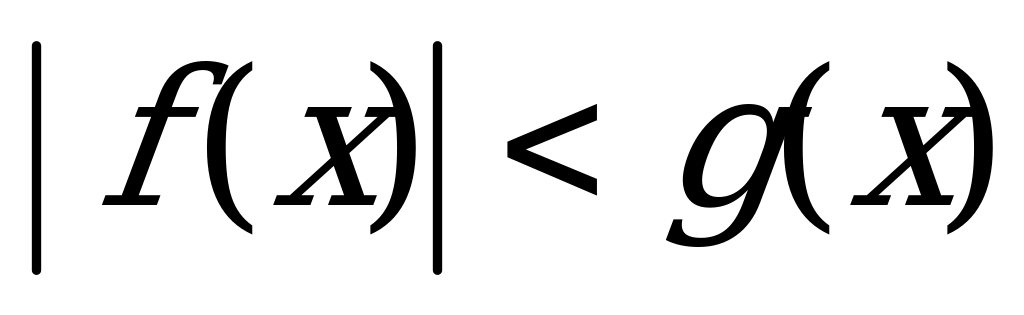

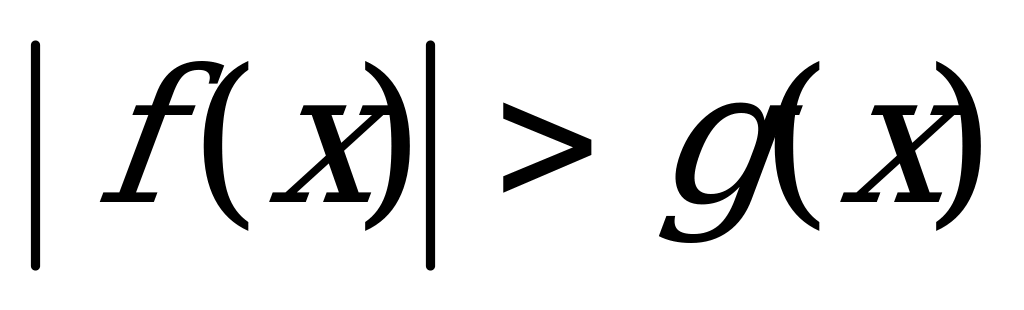

8) Неравенства, содержащие алгебраическую сумму двух и более модулей, решаются методом разбиения на промежутки по той же схеме, что и аналогичные уравнения.
Методы решения уравнений и неравенств,
содержащих переменную под знаком модуля
Материал проекта представлен в виде практических тестов, которые позволят систематизировать и качественно улучшить уровень решения задач, содержащих неизвестную под знаком модуля. В тестах содержится достаточно большое количество заданий и упражнений, взятых из различных источников, при этом предпочтение отдавалось комбинированным упражнениям, при решении которых используются сведения из различных разделов элементарной математики. Все задания направлены на развитие интереса к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач.
Уравнения с модулем
Для решения уравнений, содержащих переменную под знаком модуля, обычно применяется один из методов:
раскрытие модуля по определению;
возведение обеих частей уравнения в квадрат;
метод разбиения на промежутки.
Первый из способов обычно применяется, когда в уравнении встречается лишь одно выражение под знаком модуля; второй – когда обе части уравнения, возводимые в квадрат, неотрицательны; третий – когда в уравнении встречается несколько выражений, стоящих под знаком модуля.
Пример. 1а). Решите уравнение 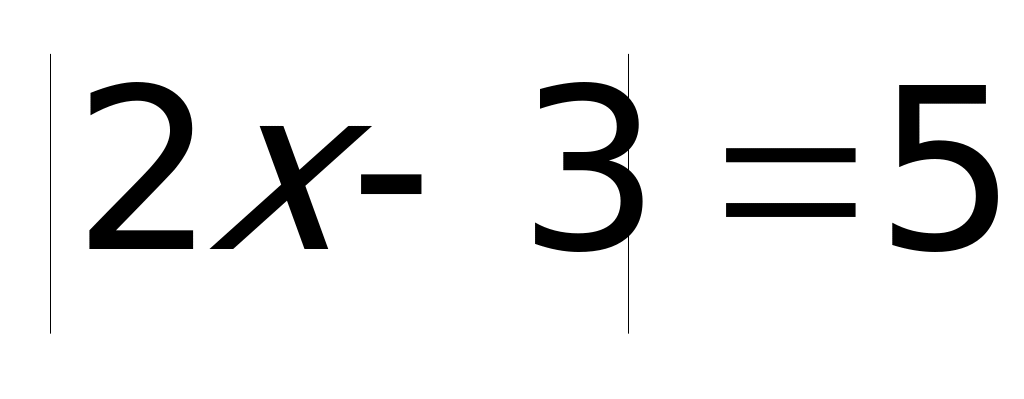
Решение: Первый способ: Воспользуемся определением модуля и получим совокупность двух систем:
Из первой системы совокупности находим 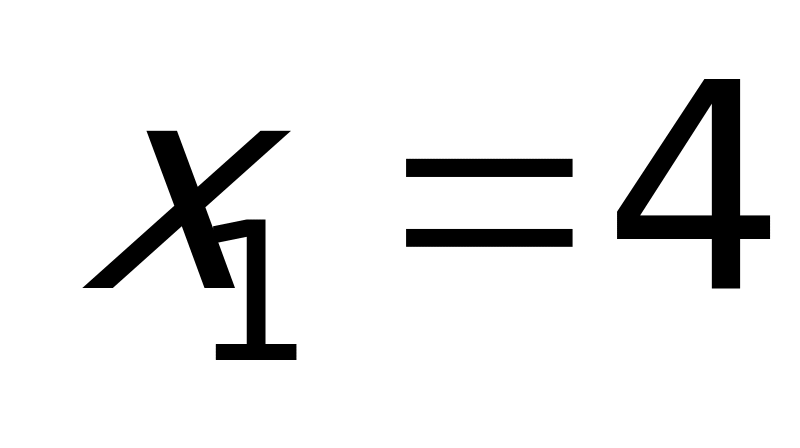
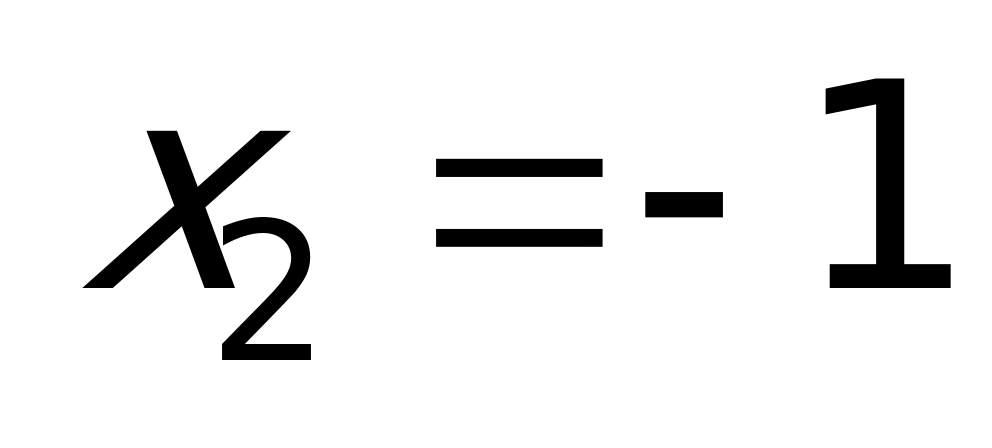
Второй способ: Так как обе части данного уравнения неотрицательны, то можно получить равносильное уравнение: 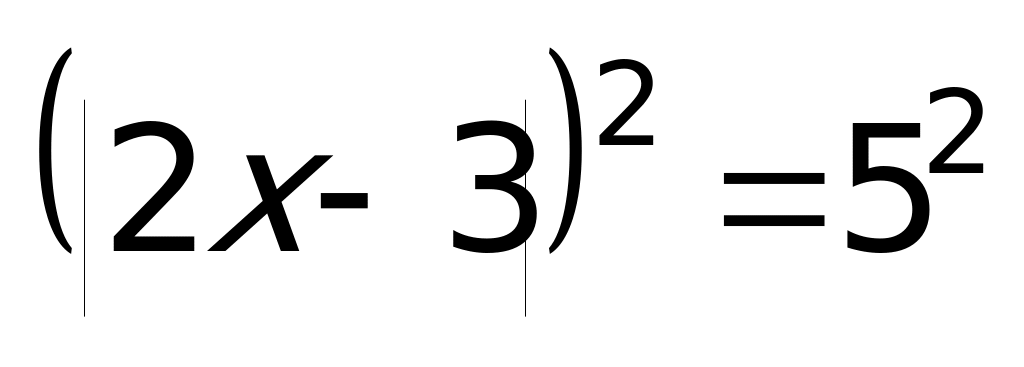
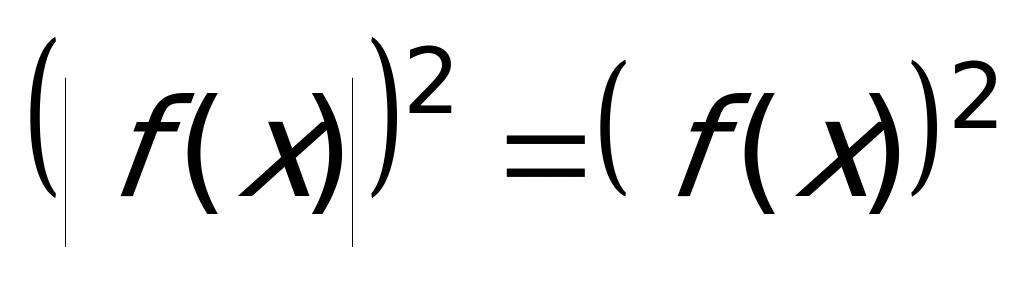
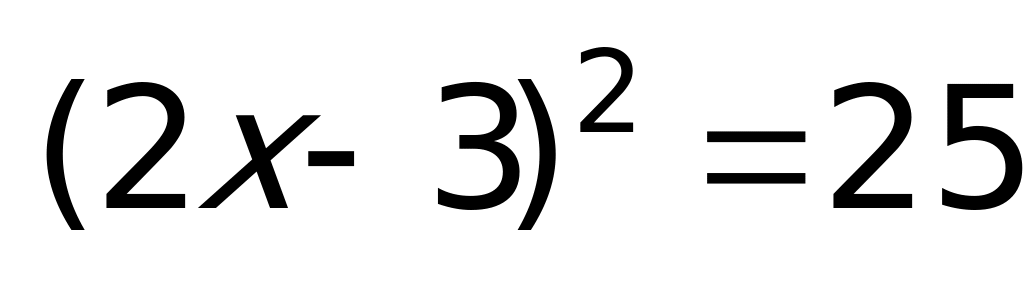
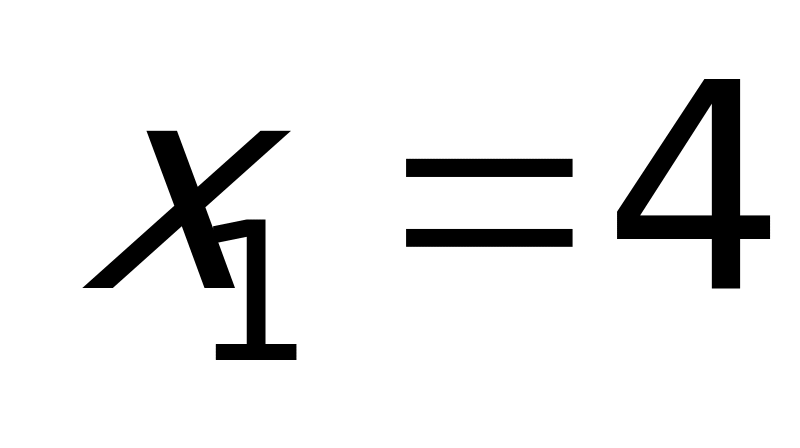
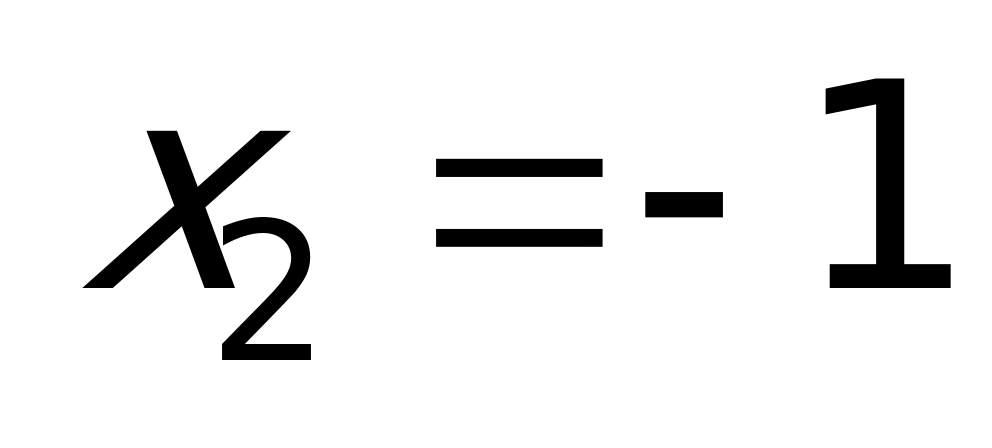
Ответ: 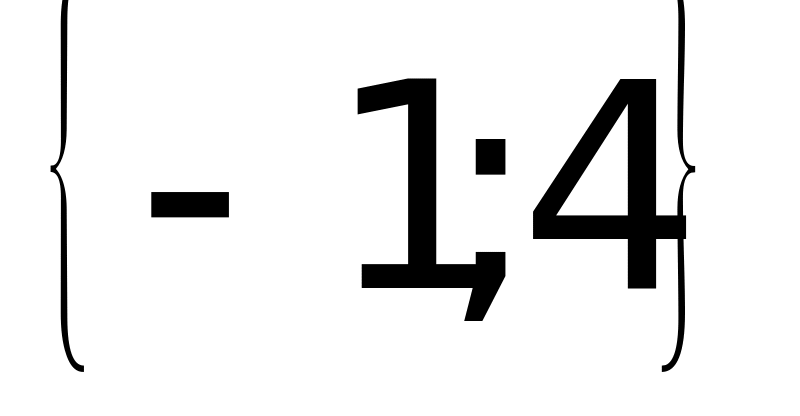
Пример 1б). Сумма корней уравнения 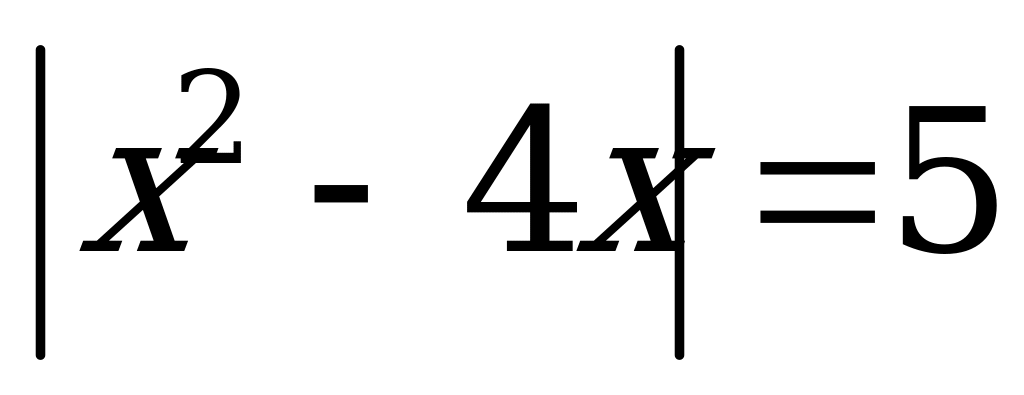
А) 4 B) 5 C) –4 D) 3 E) 2
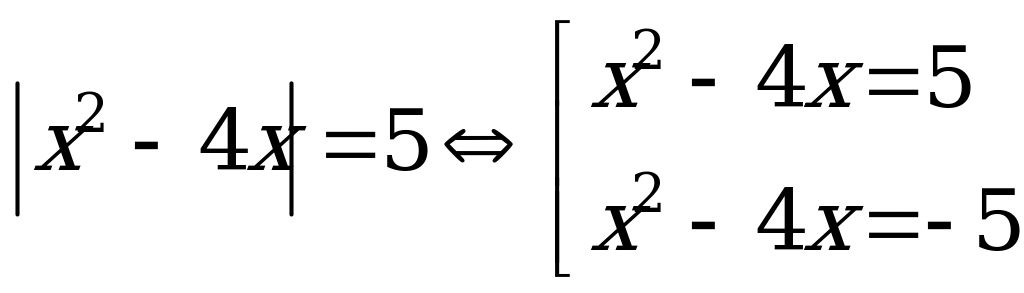
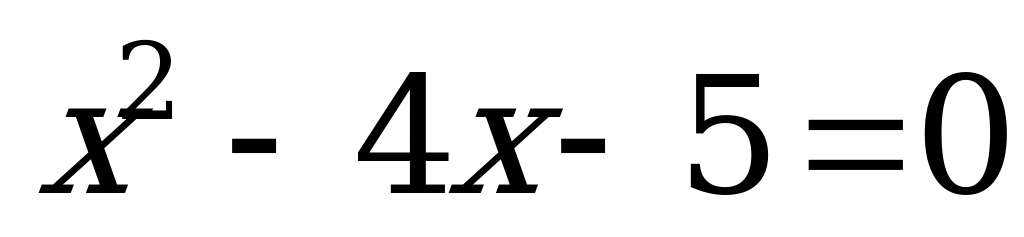
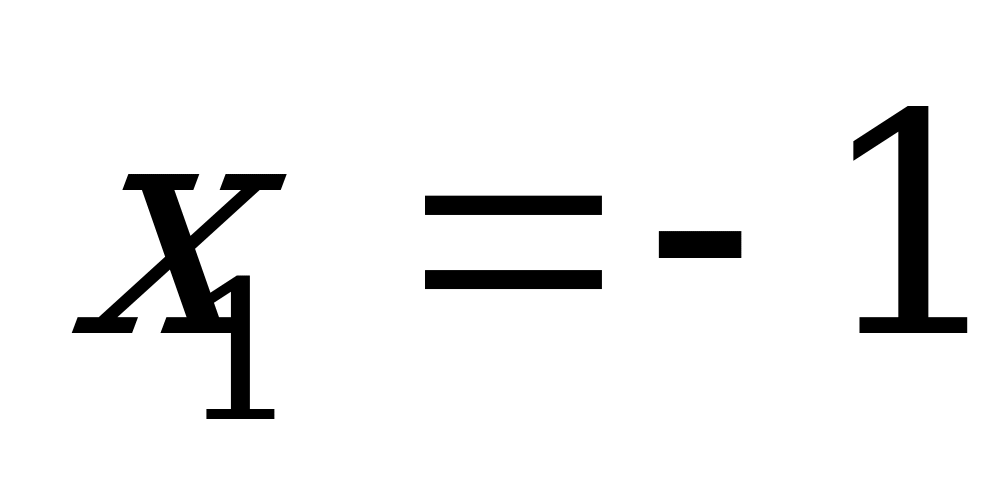
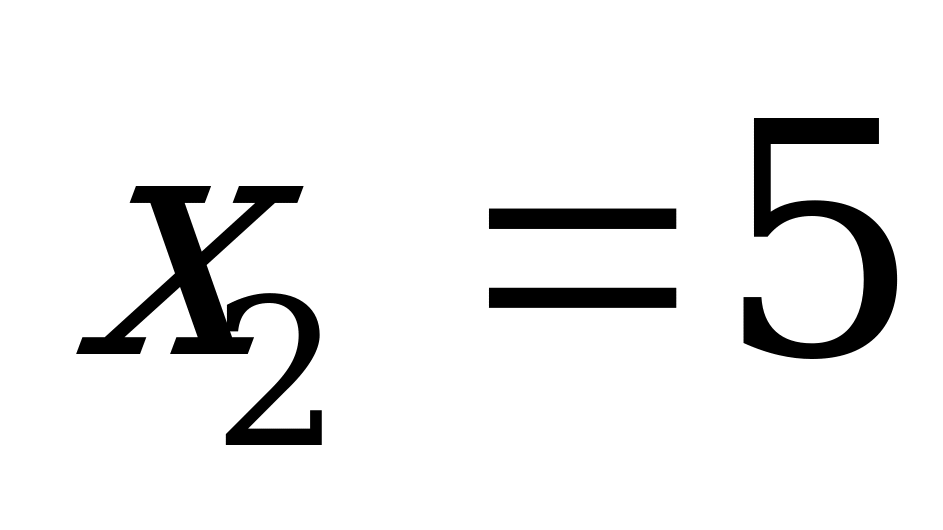
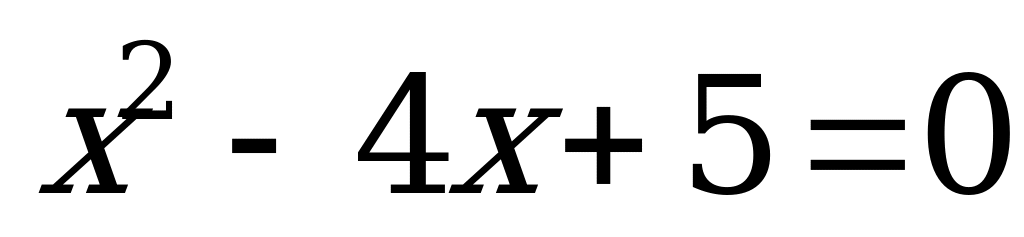
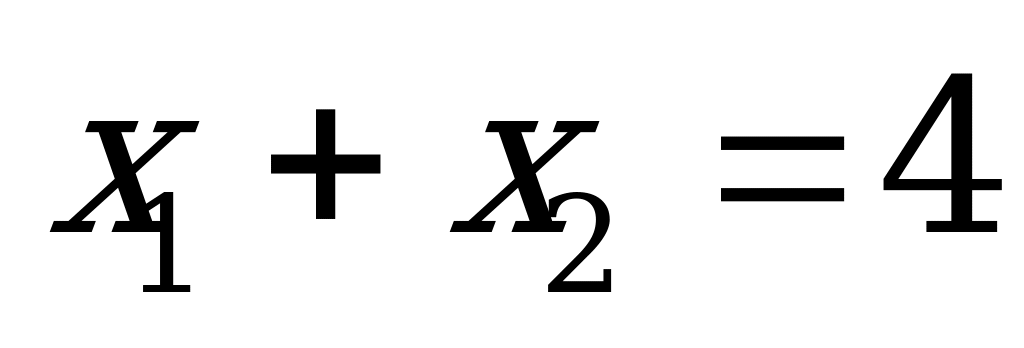
Пример 2. Сумма корней уравнения 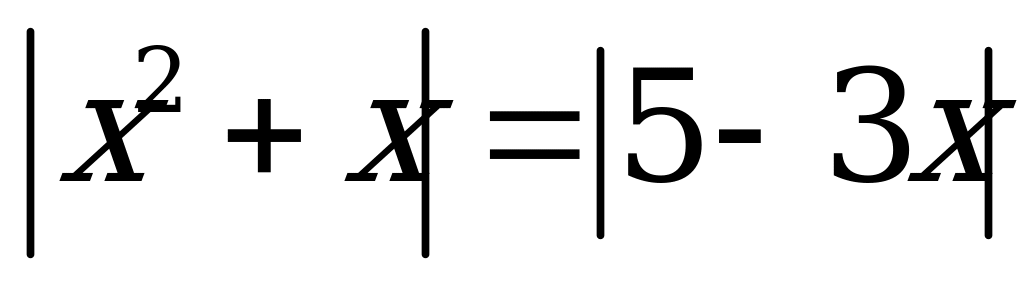
А) 4 B) –5 C) –4 D) 3 E) 5
Решение. 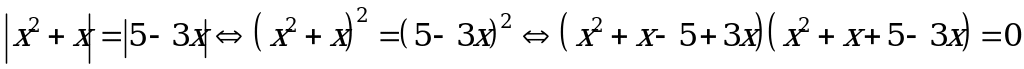
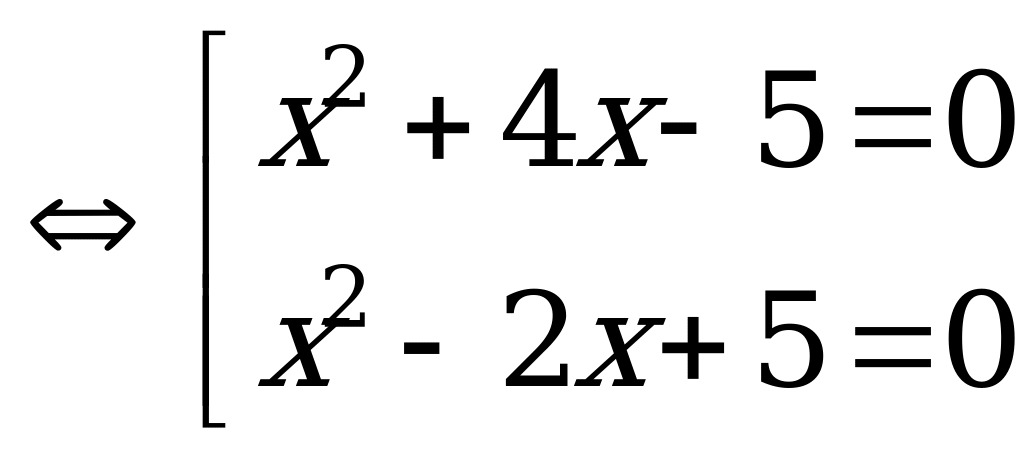
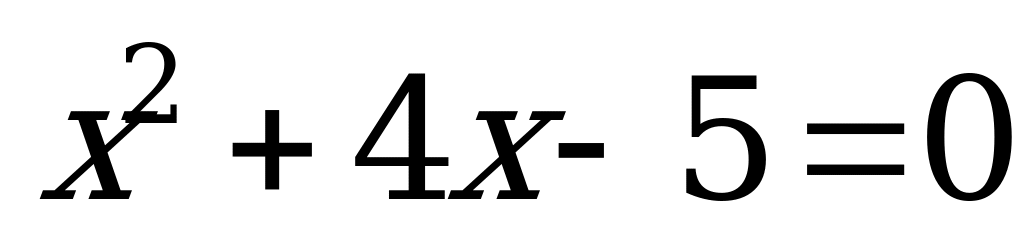
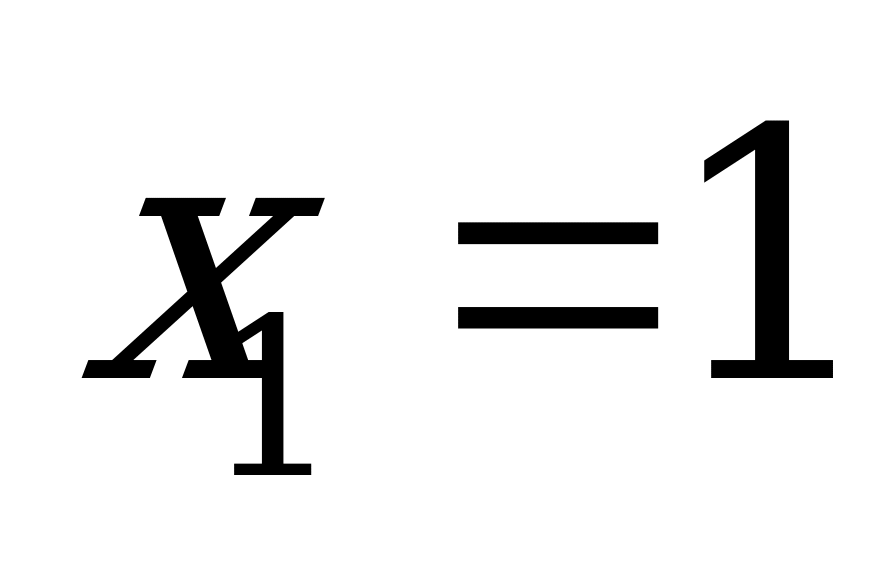
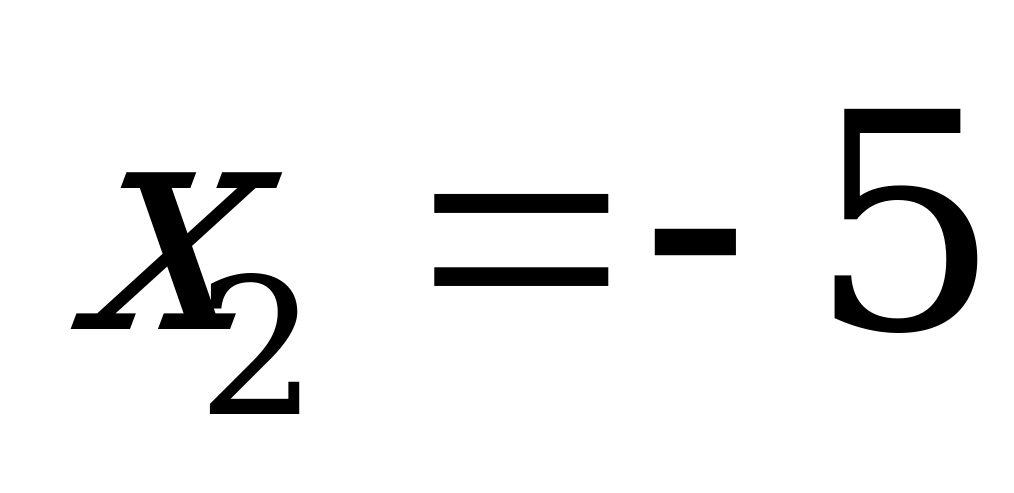
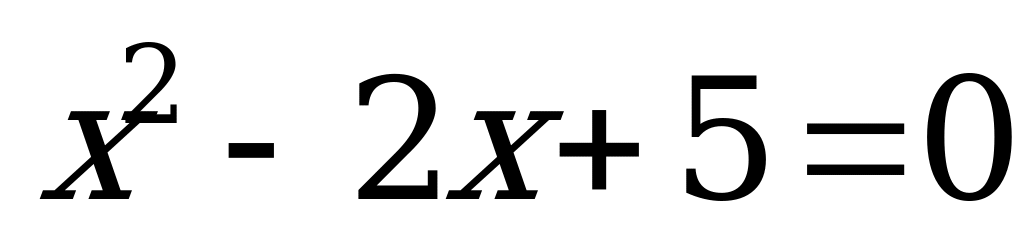
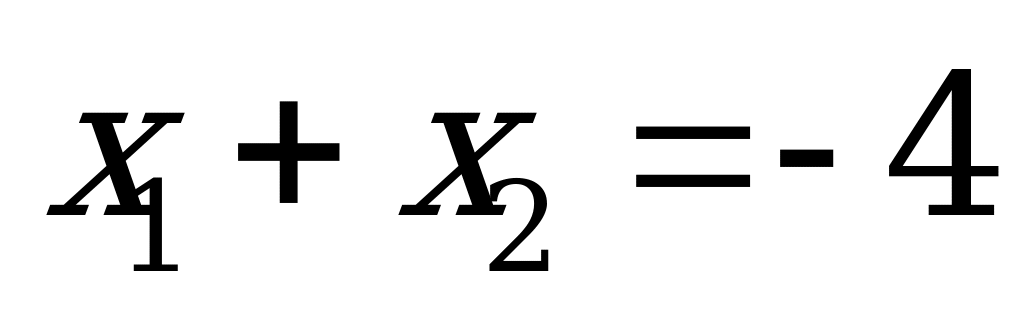
Пример 3а) Решите уравнение 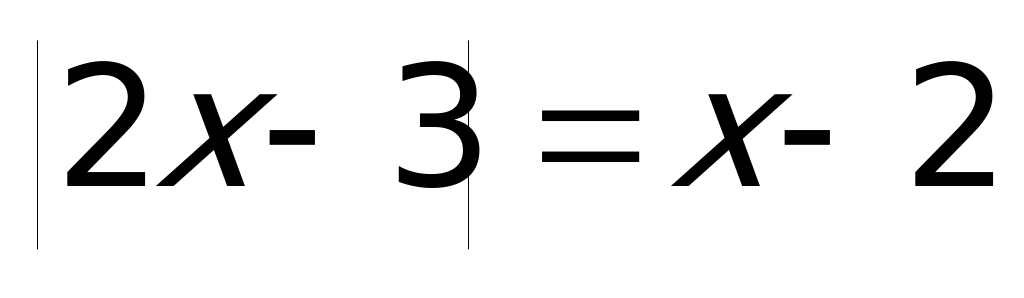
Решение. Воспользуемся для решения вторым способом. Ясно, что если 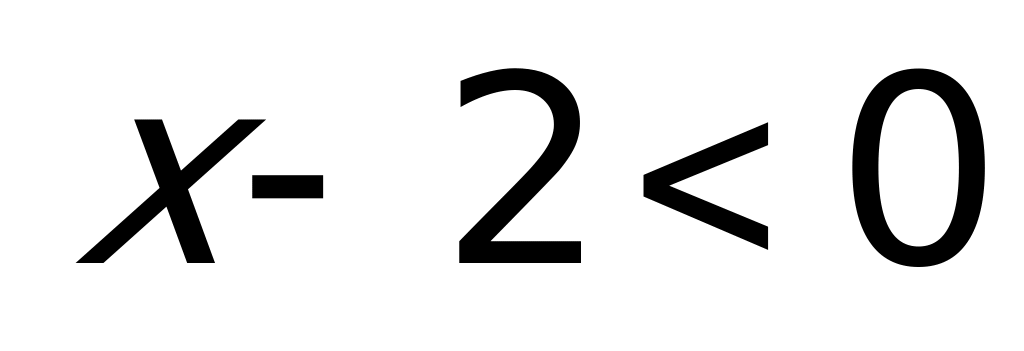
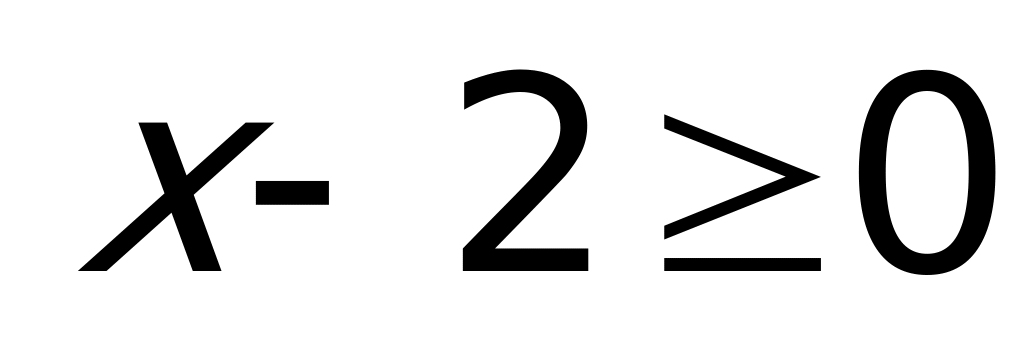
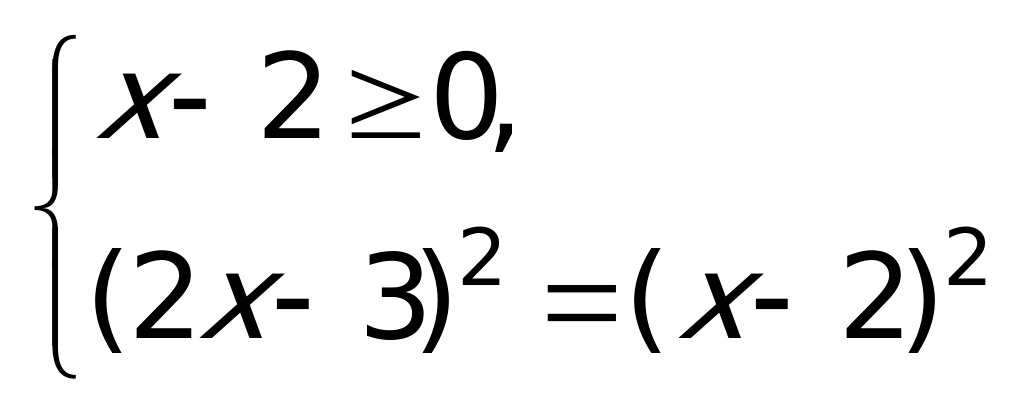
Последняя система корней не имеет, следовательно, и исходное уравнение тоже.
Пример 3б). Произведение корней уравнения 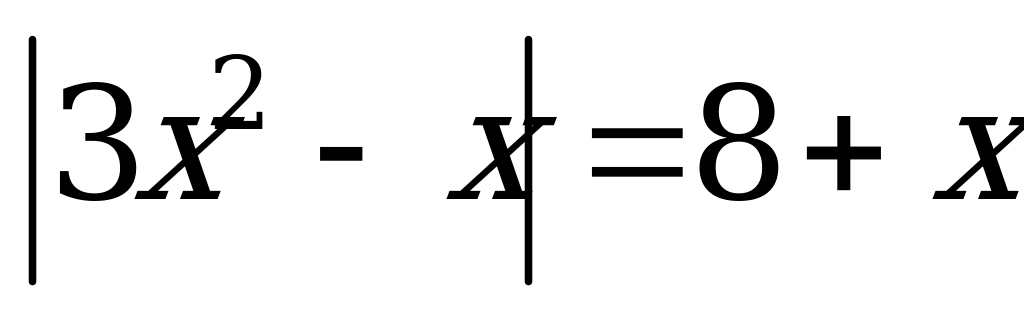
А) 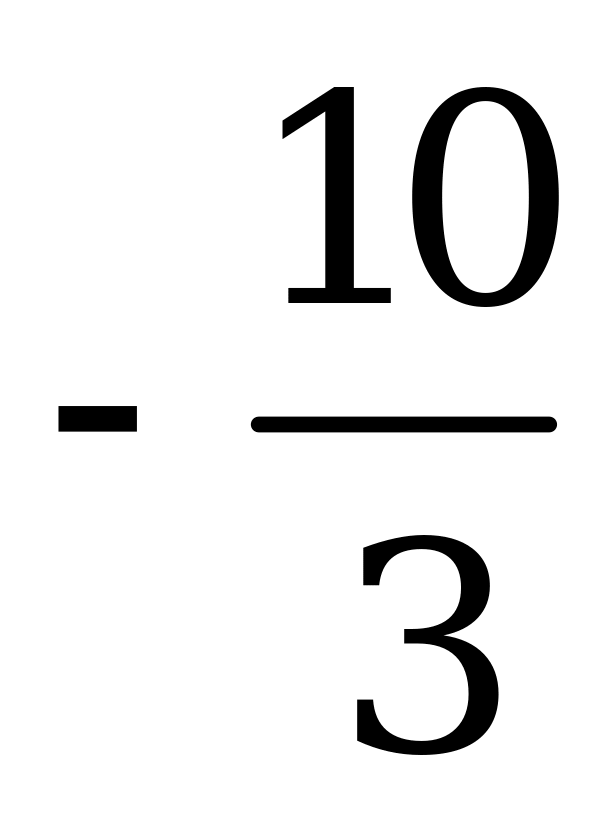
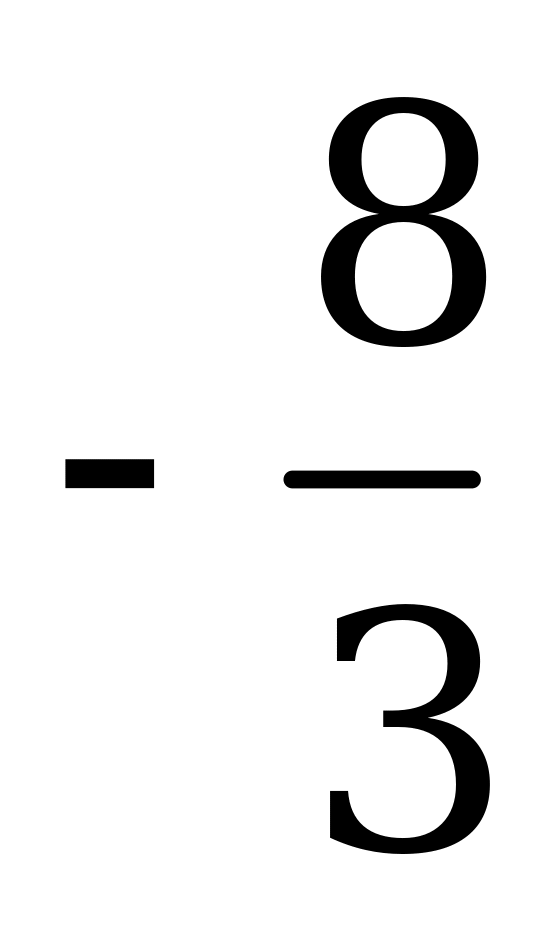
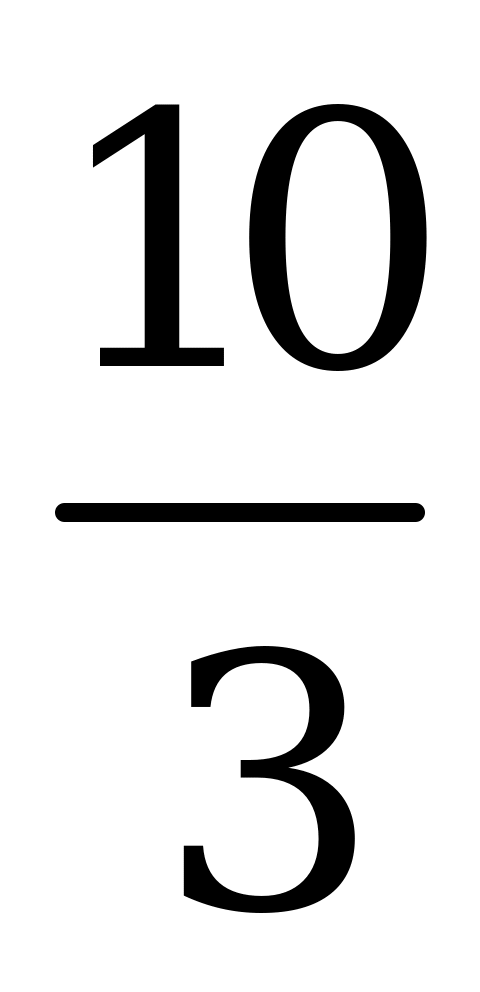
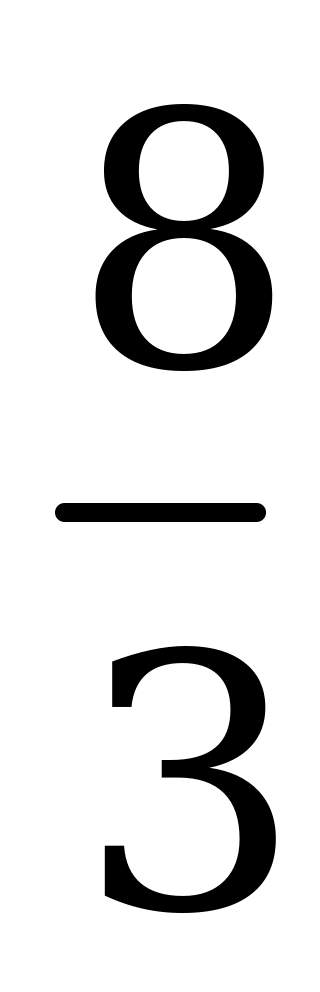
Данное уравнение равносильно системе 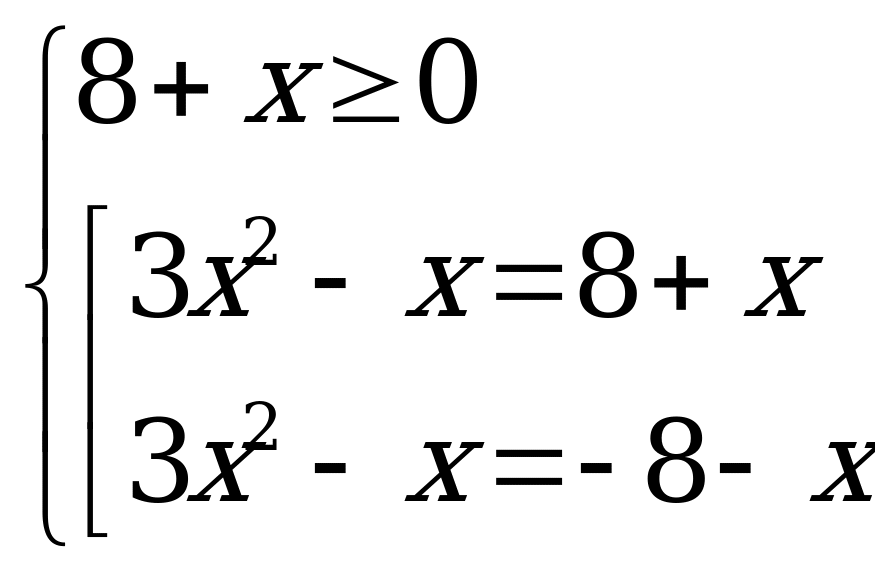
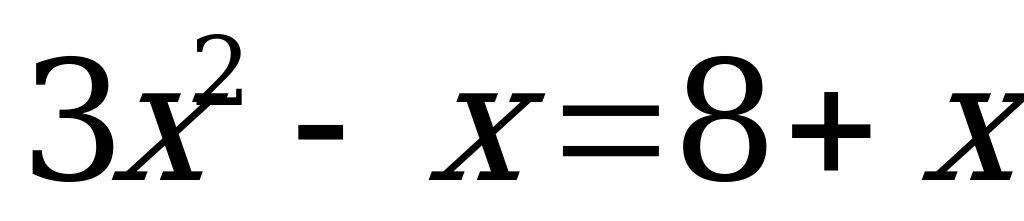
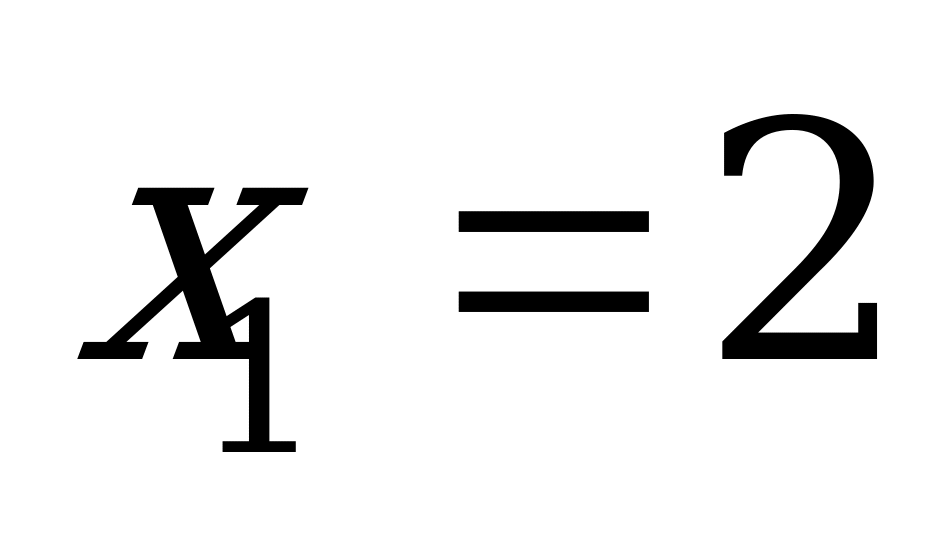
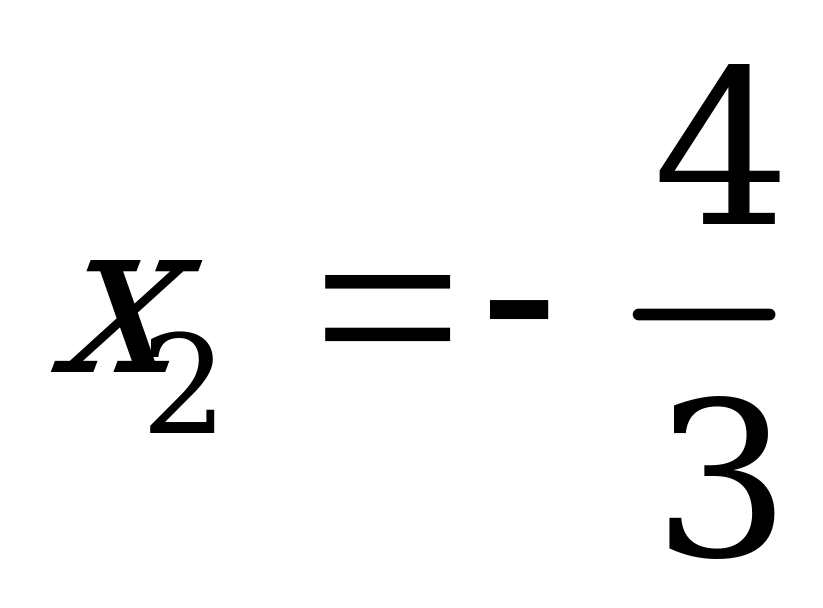
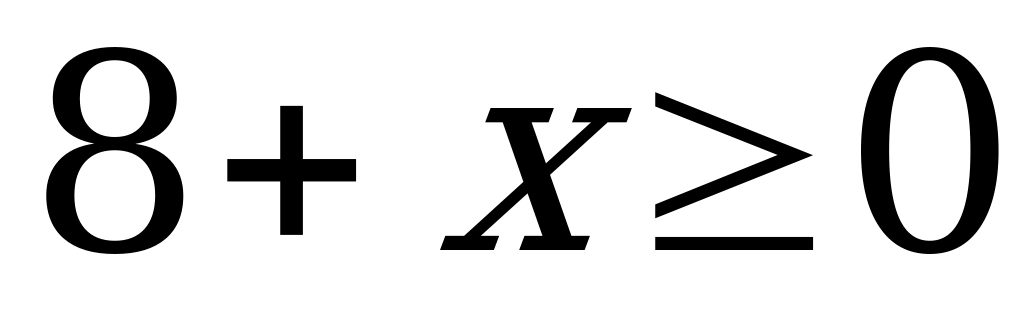
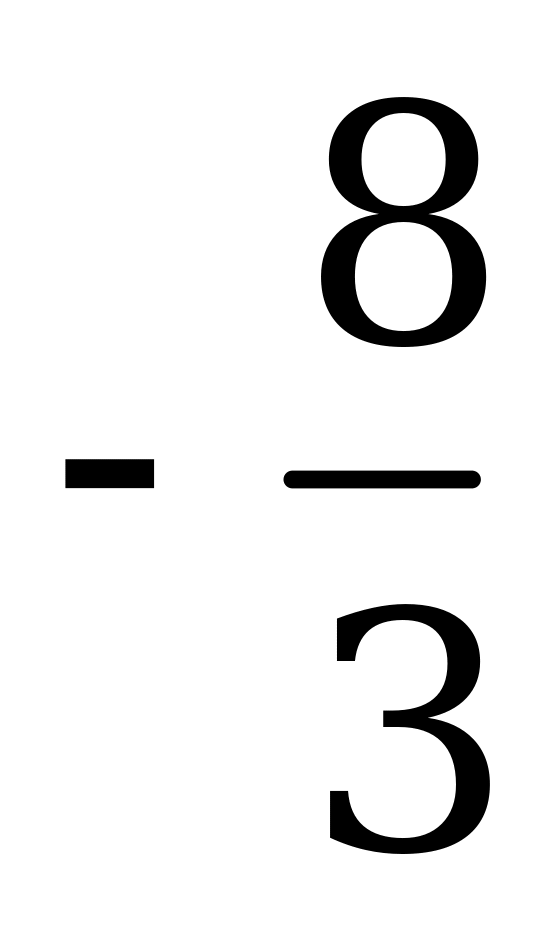
Пример 3в). Найдите сумму корней или корень, если он единственный, уравнения 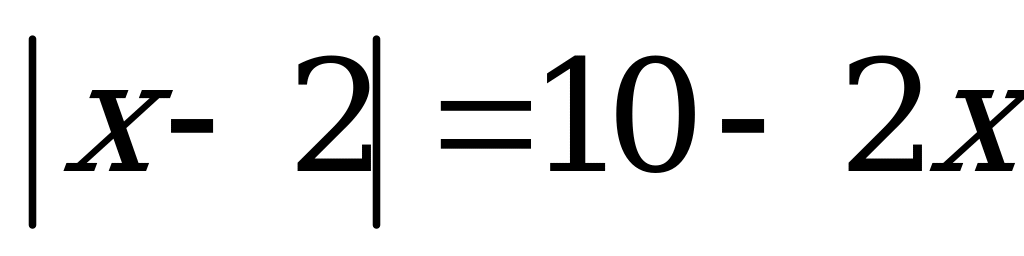
Решение. Данное уравнение равносильно системе 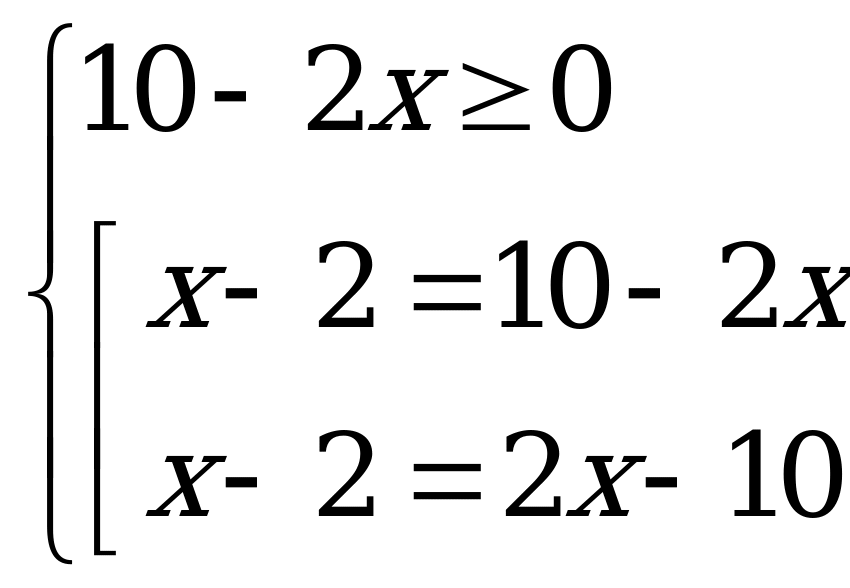
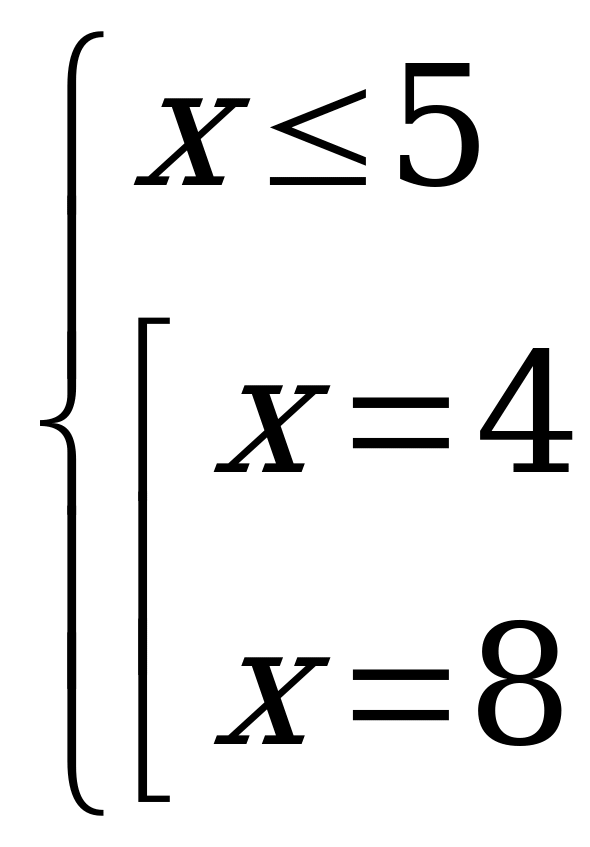
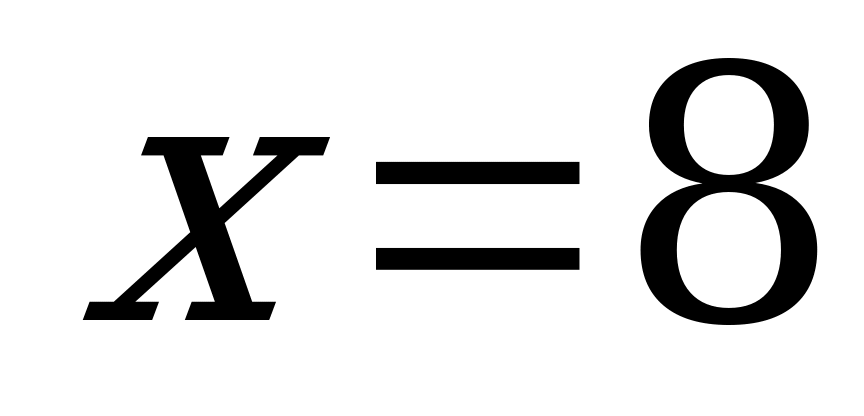
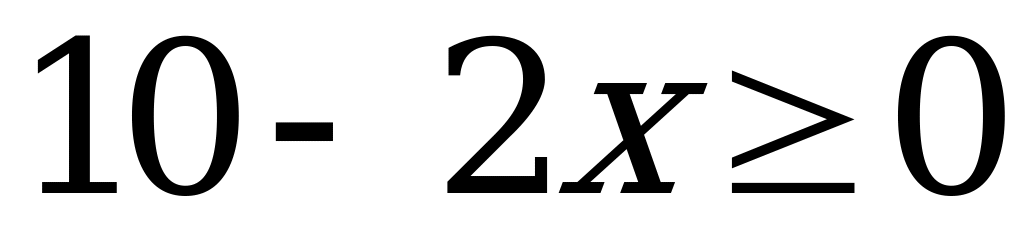
При решении уравнений третьим способом находятся те значения переменной, в которых хотя бы одно из выражений, стоящих под знаком модуля, обращается в 0. Этими точками вся числовая прямая разбивается на промежутки (отсюда и название метода). Далее на каждом из полученных промежутков решается исходное уравнение, при этом каждый модуль раскрывается по определению. Для этого удобно заранее оценить знаки каждого из выражений, стоящих под модулем, и полученные результаты свести в таблицу. Полученные ответы проверяются на принадлежность промежутку, на котором велось решение. Множеством решений исходного уравнения является объединение корней, полученных на каждом из промежутков.
Пример 4а) Решите уравнение 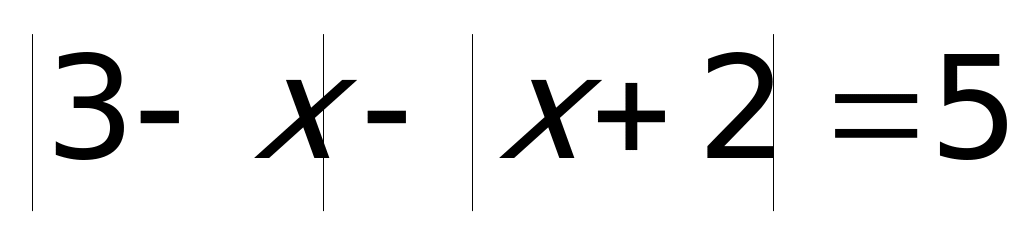
Решение: Применим метод разбиения на промежутки. 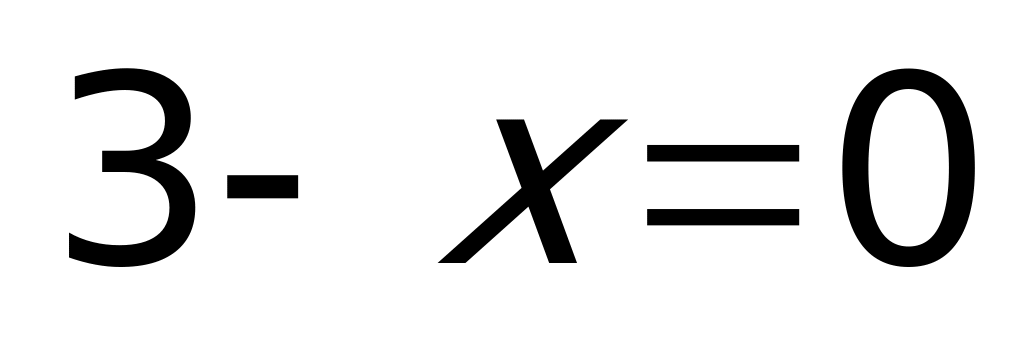
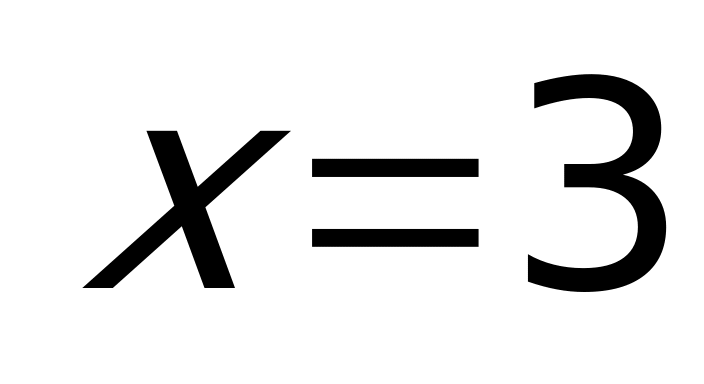
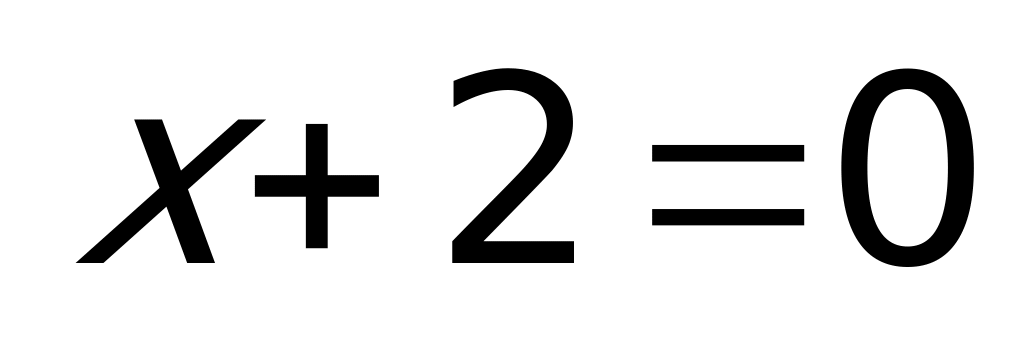
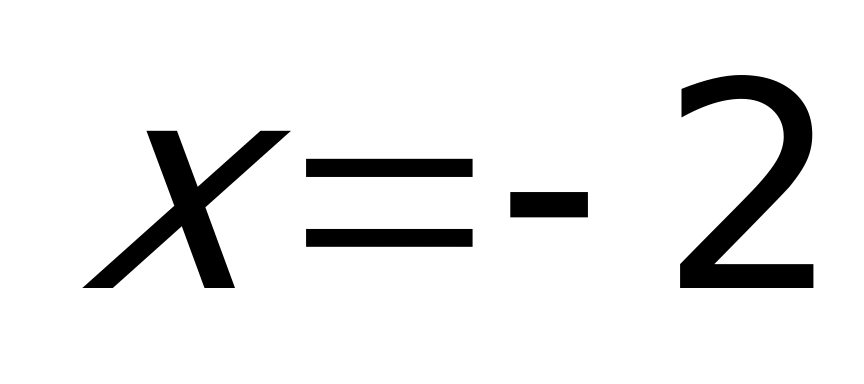
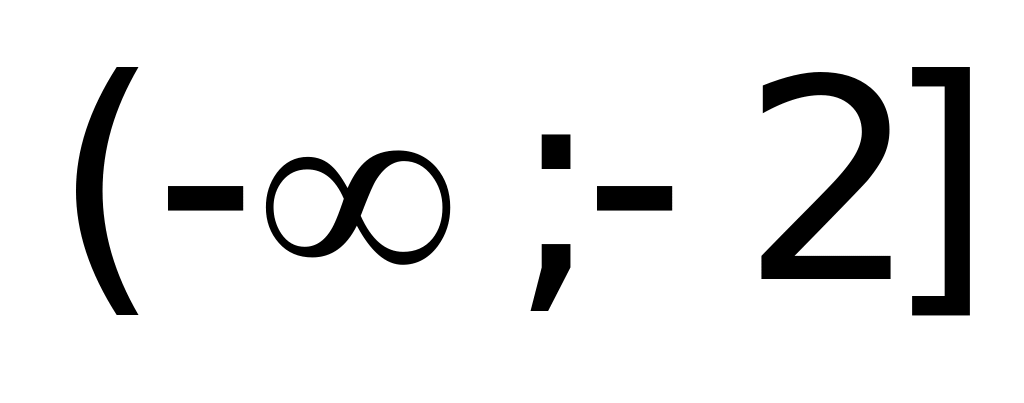
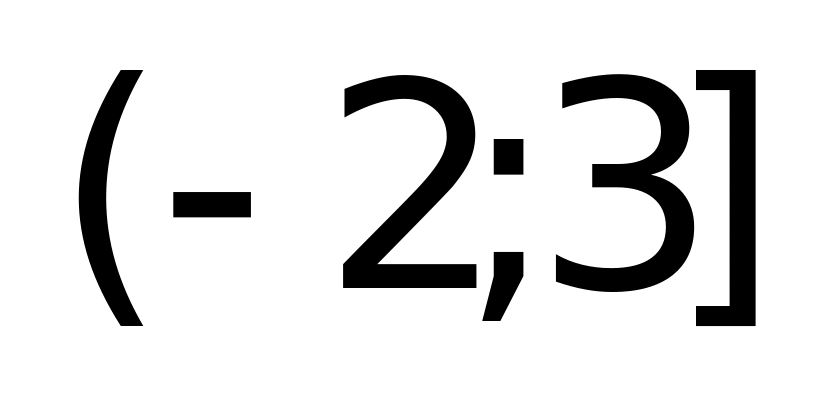
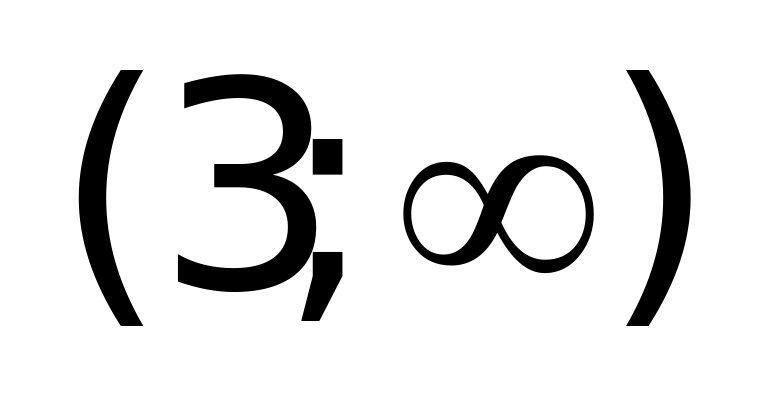
(“+” – выражение на указанном промежутке положительно,
“—“ – отрицательно).
Рассмотрим каждый промежуток:
1) 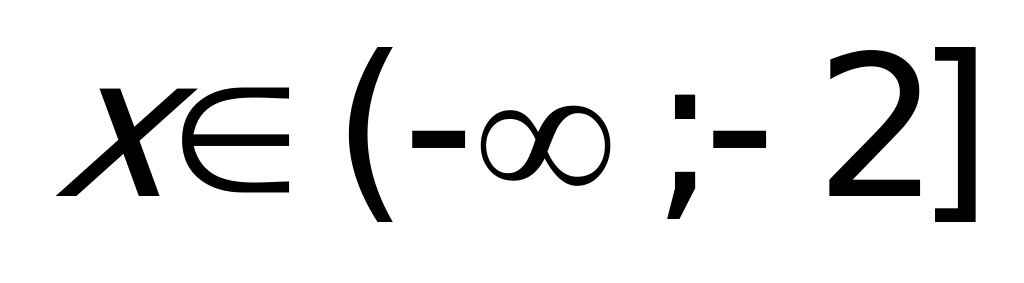
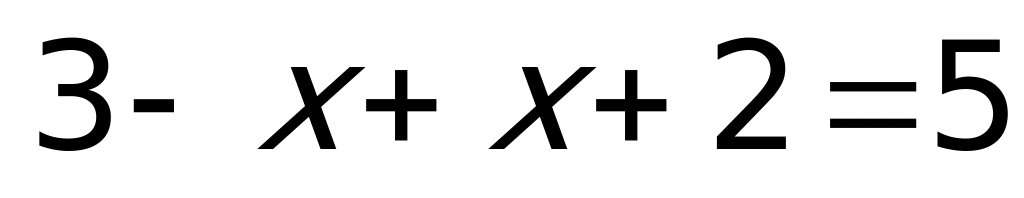
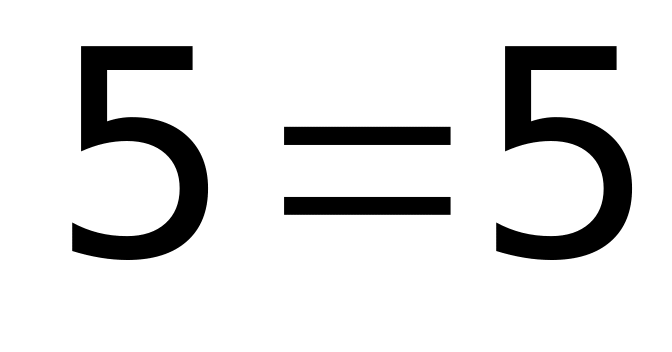
2) 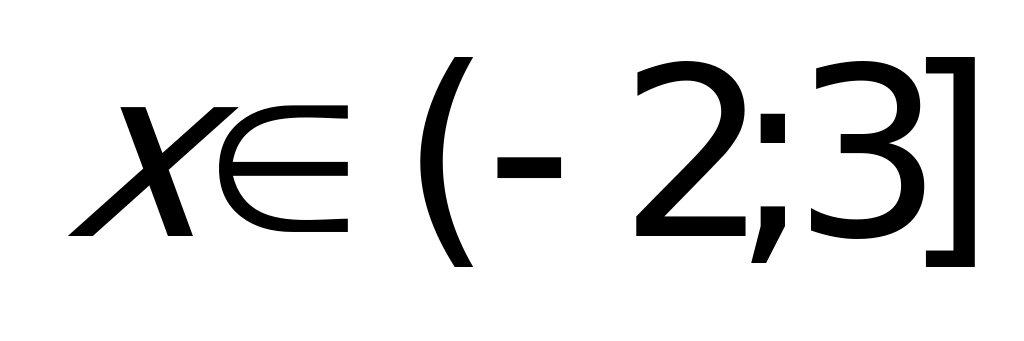
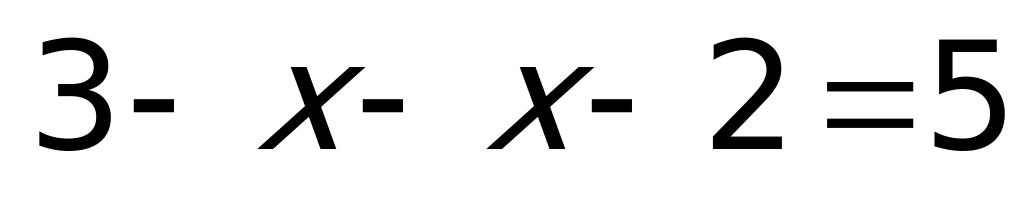
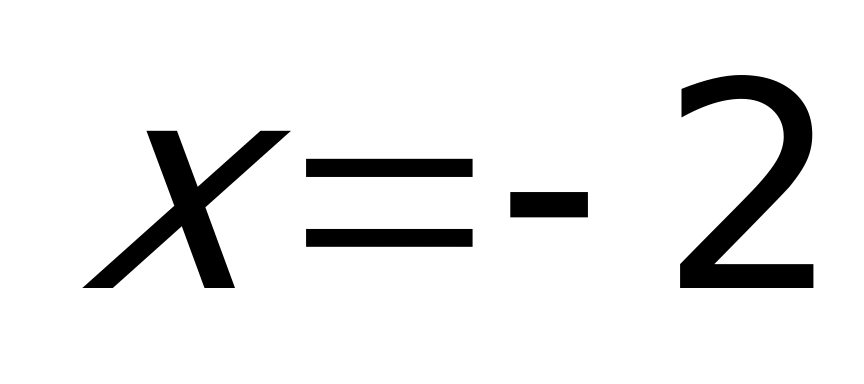
3) 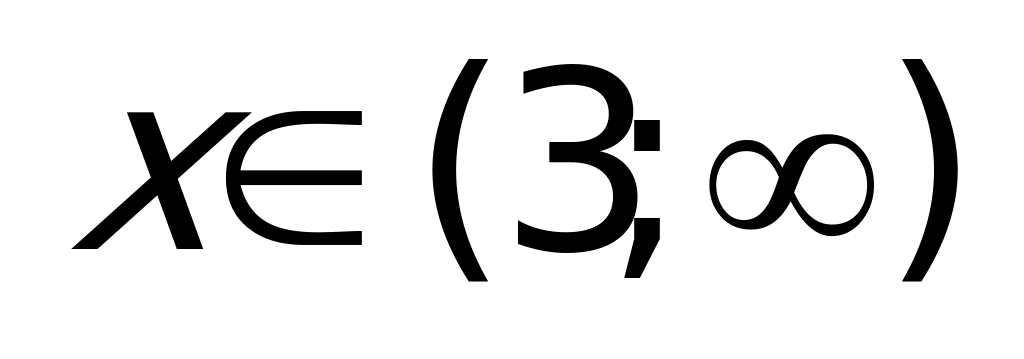
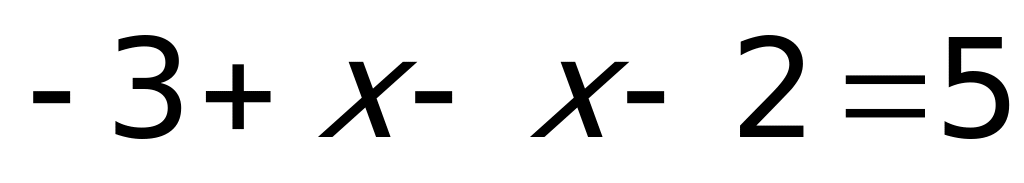
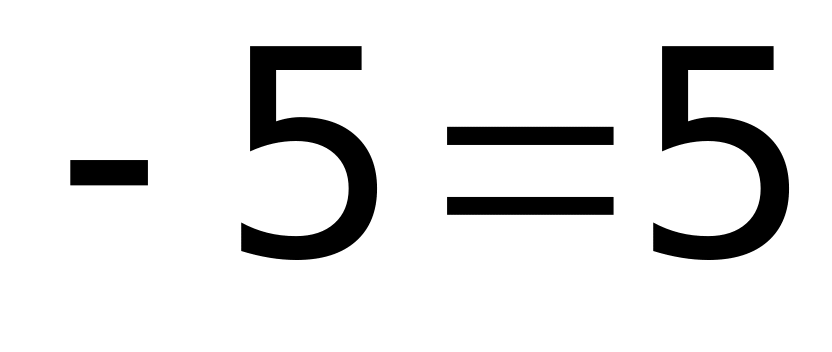
Объединяя результаты пунктов 1, 2 и 3, получаем ответ.
Ответ: 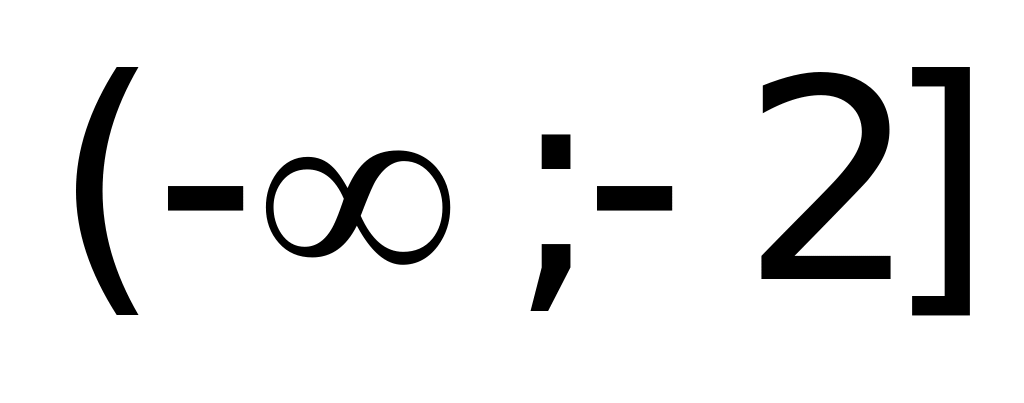
Пример 4б). Сумма корней уравнения 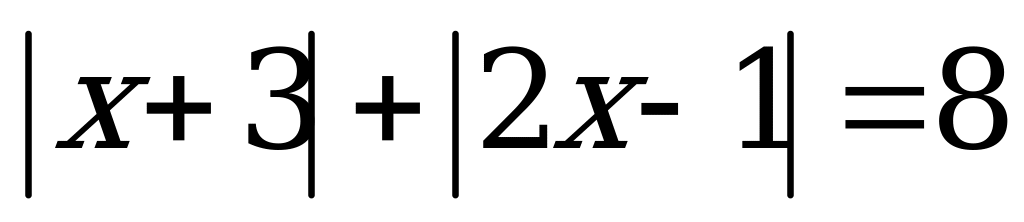
А) 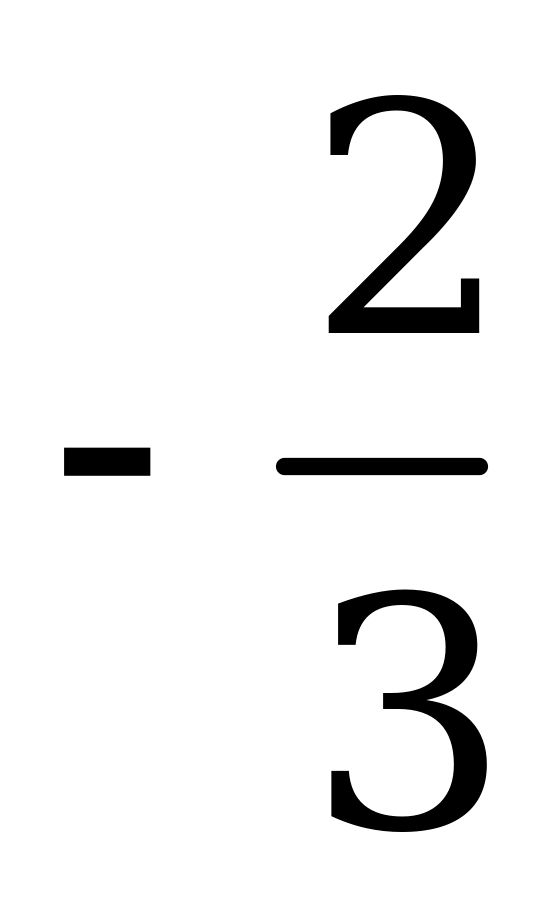
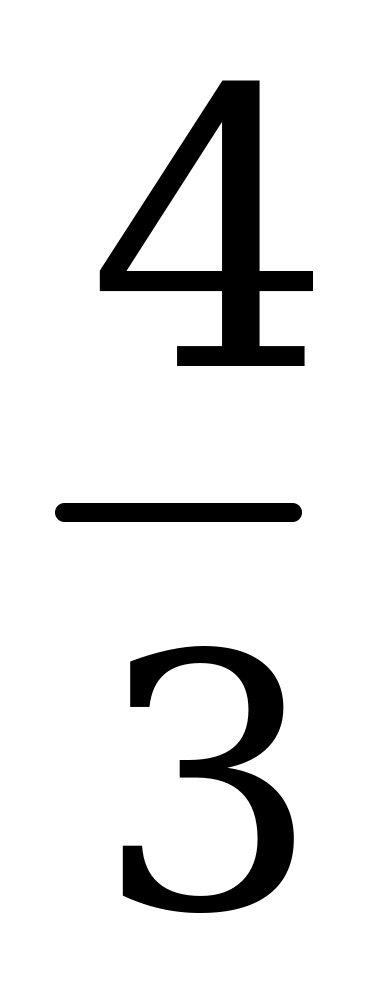
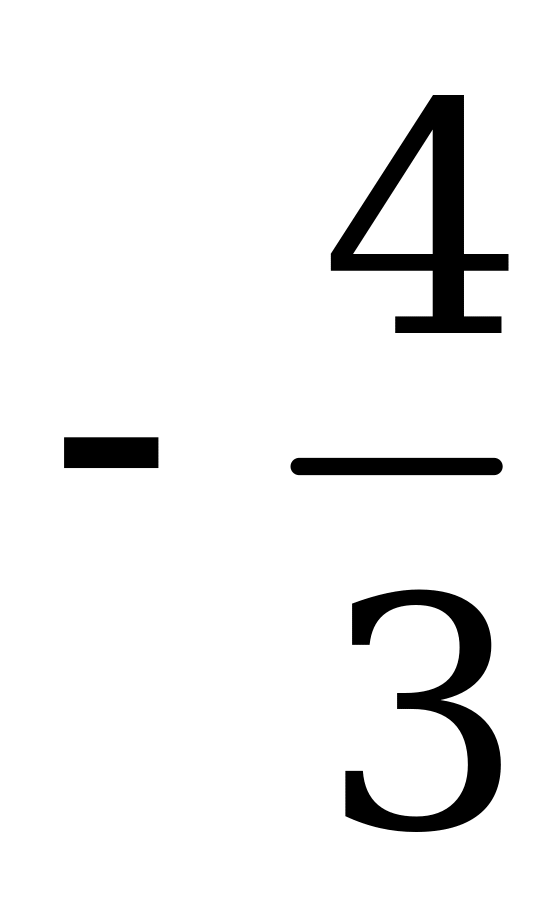
Решение. Выражения под знаками модуля обращаются в ноль в точках 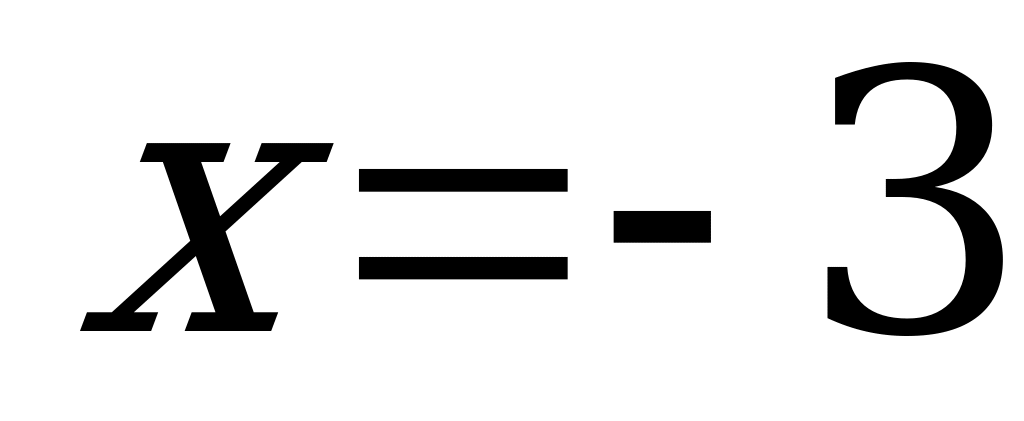
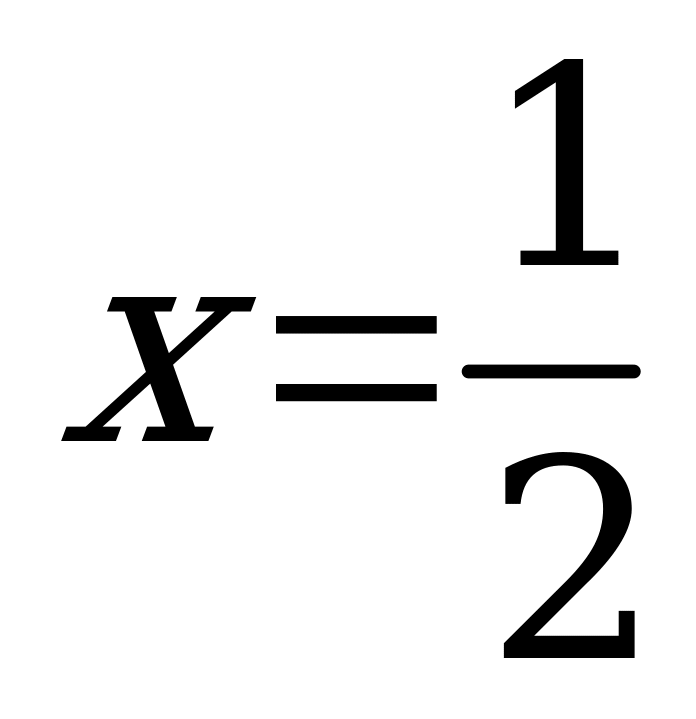
Итак, сумма корней данного уравнения 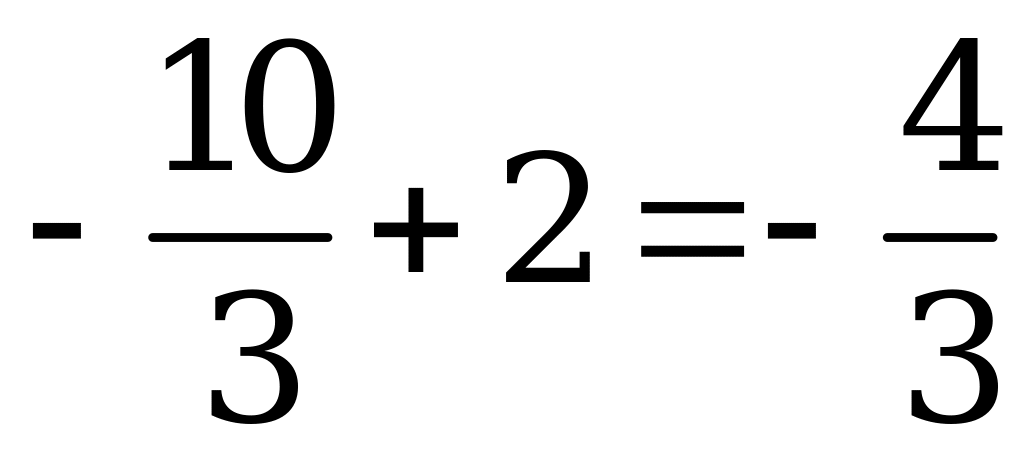
Тест «Уравнения с модулем»
Сумма корней уравнения 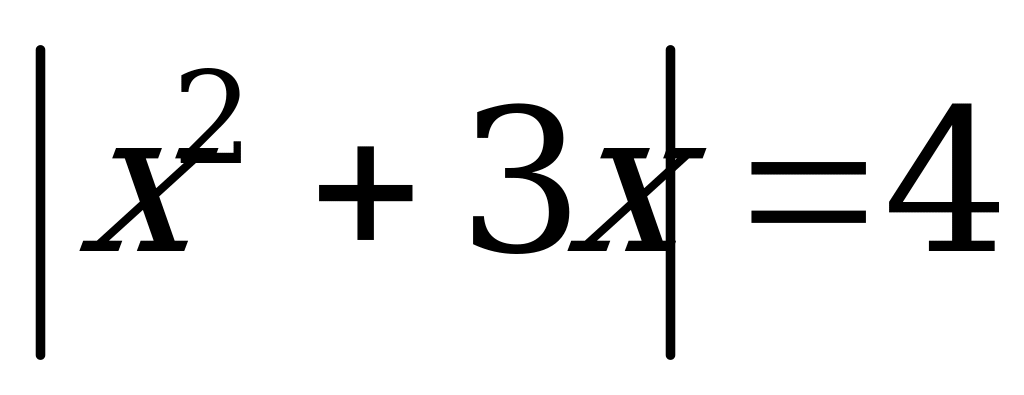
А) – 4 B) 4 C) –3 D) 3 E) 2
Сумма корней уравнения 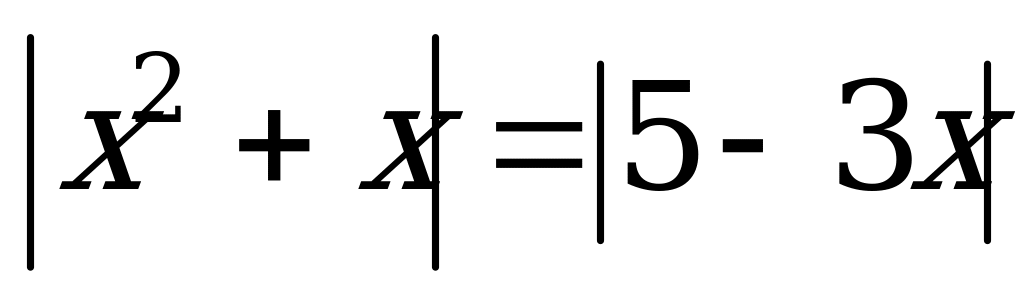
А) 4 B) –5 C) –4 D) 5 E) 3
Сумма корней уравнения 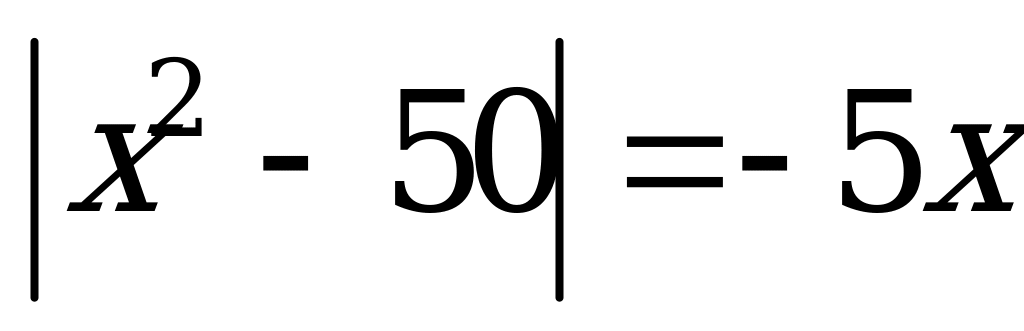
А) 0 B) 15 C) 5 D) –5 E) –15
Найдите сумму решений уравнения
А) 1 B) 2 C) 3 D) 4 E) 5
Найдите сумму корней или корень, если он единственный, уравнения
А) 1 B) –2 C) 3 D) –6 E) 8
Сумма корней или корень (если он единственный) уравнения 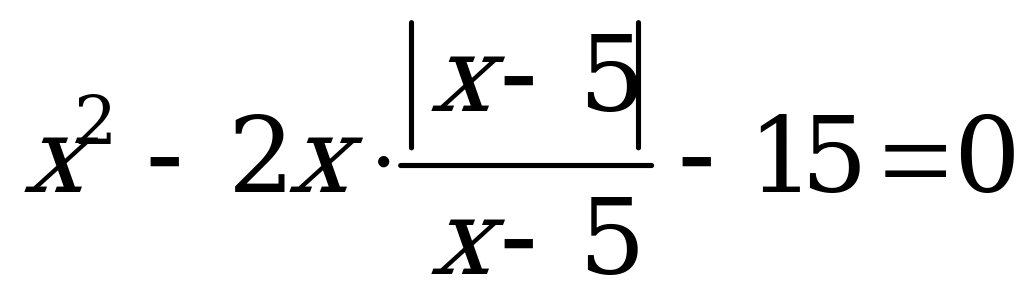
А) 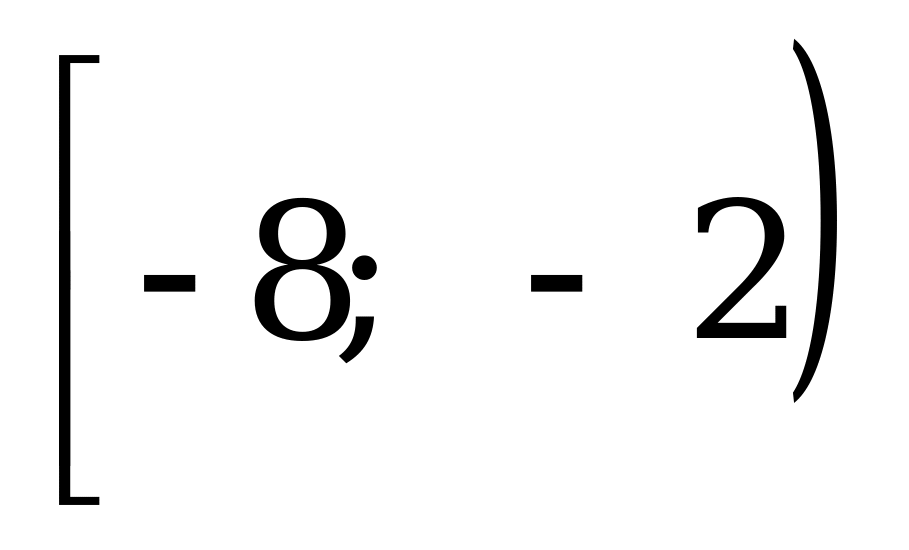
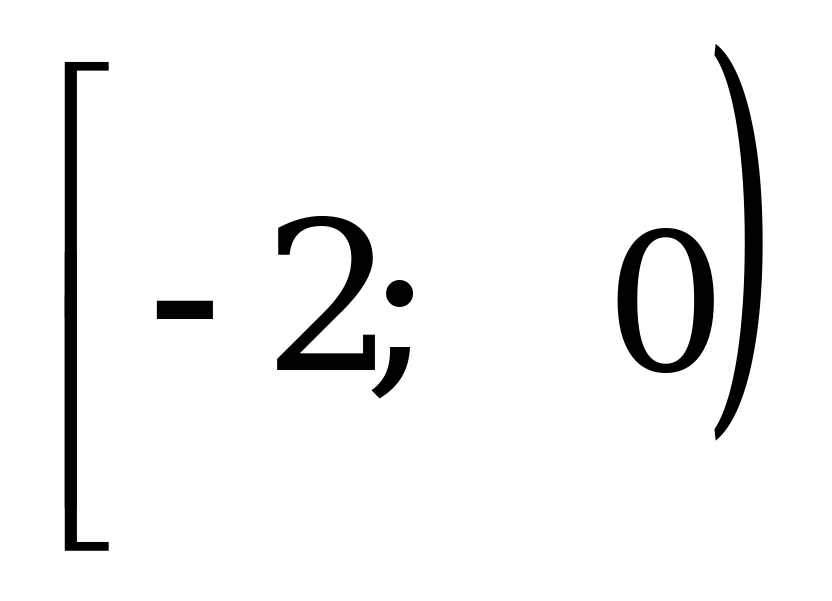
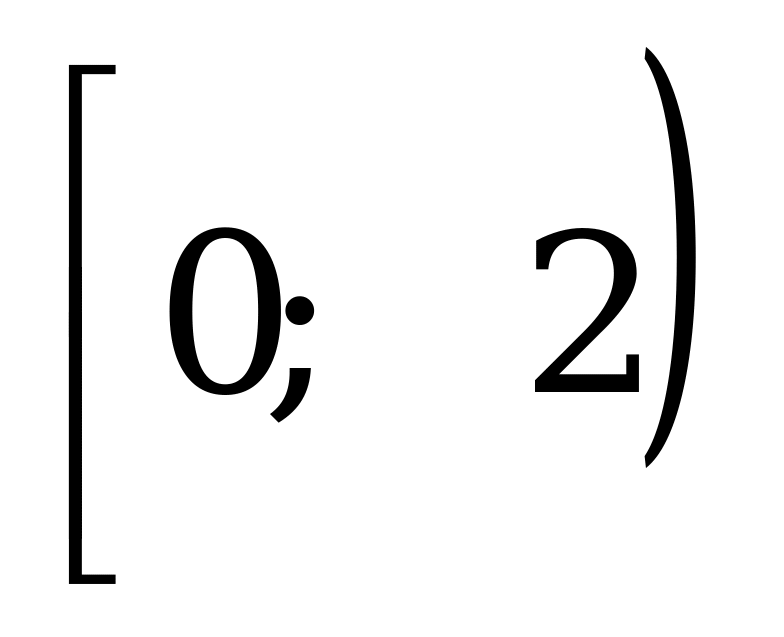
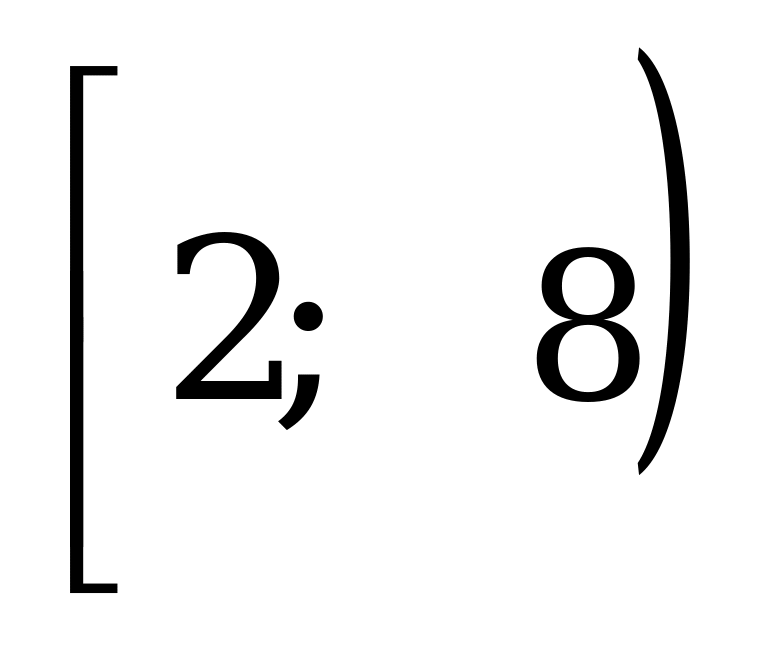
Разность между наибольшим и наименьшим корнями уравнения 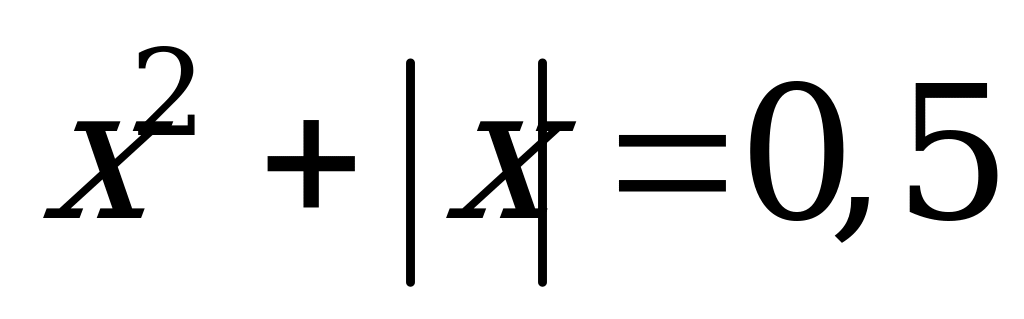
А) 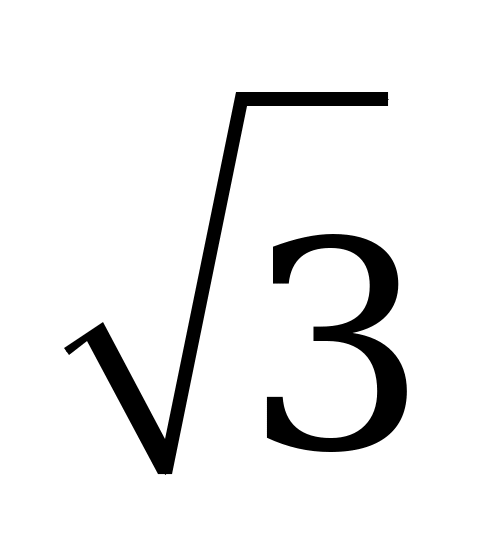
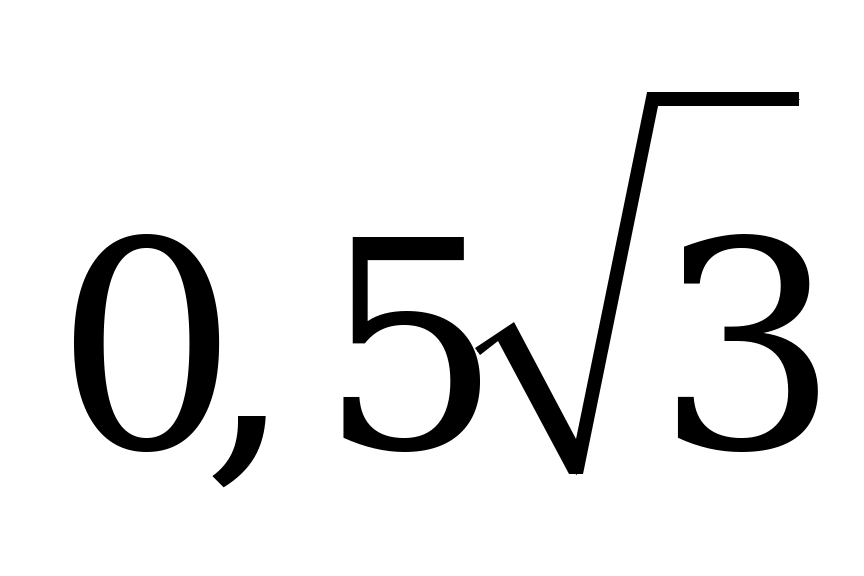
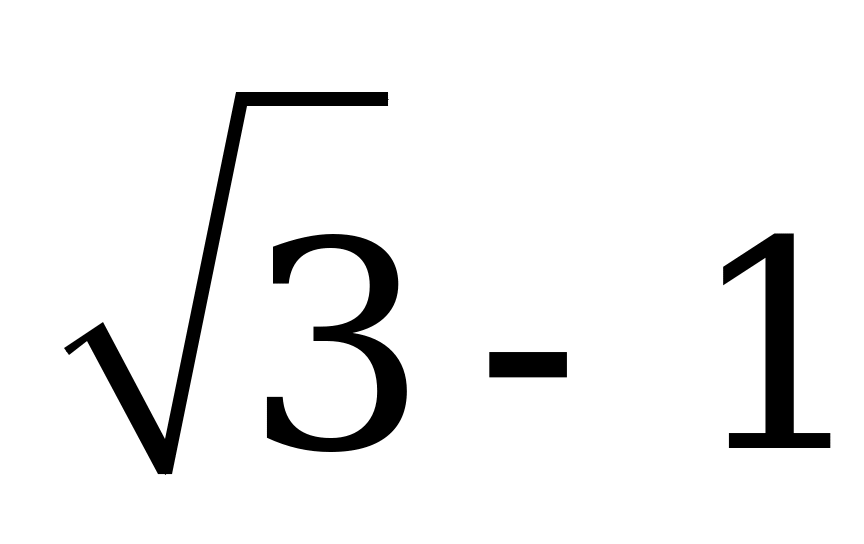
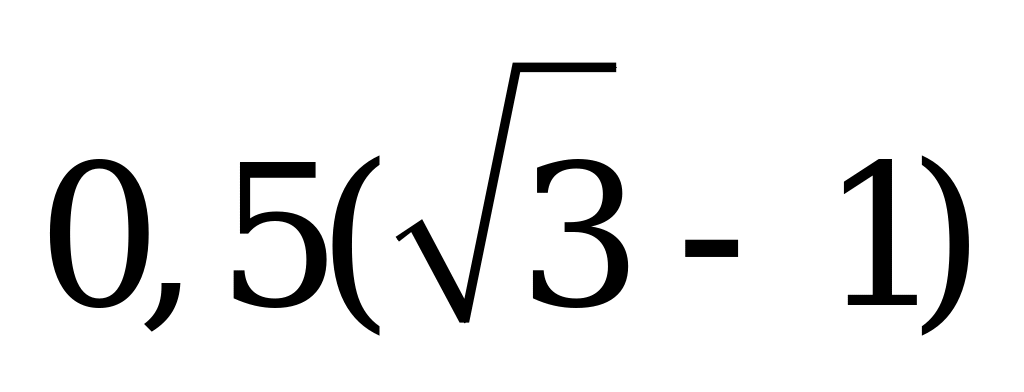
Решения уравнения 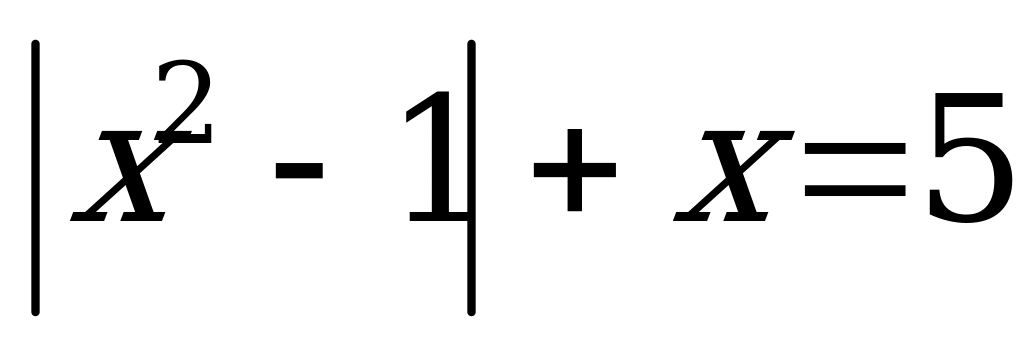
А) 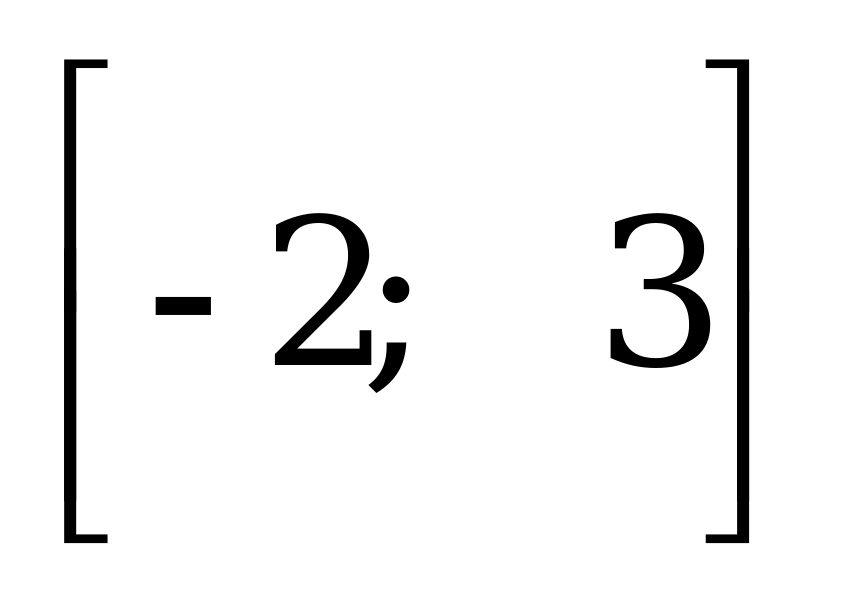
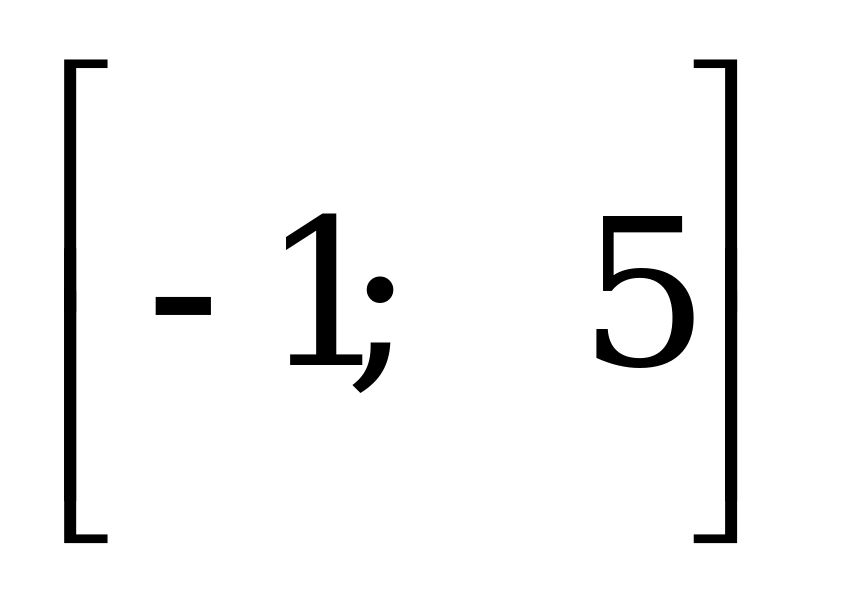
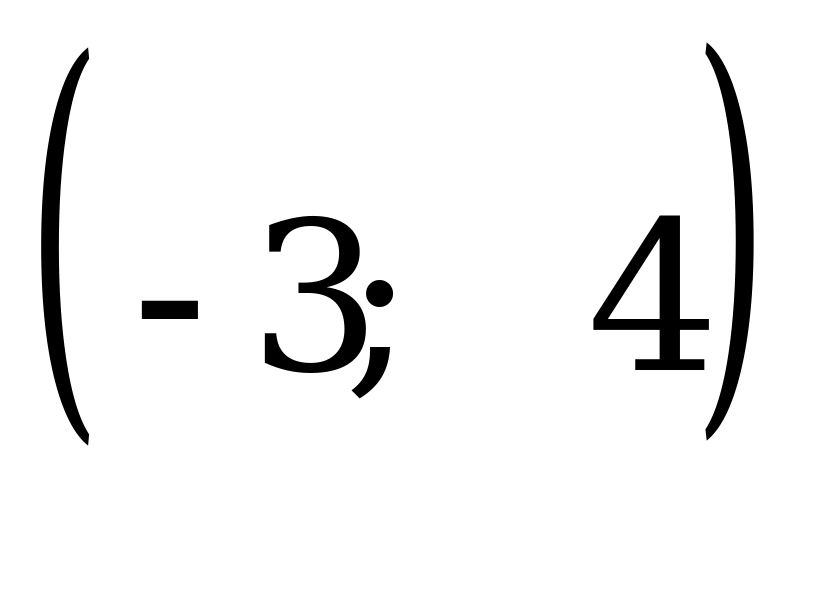
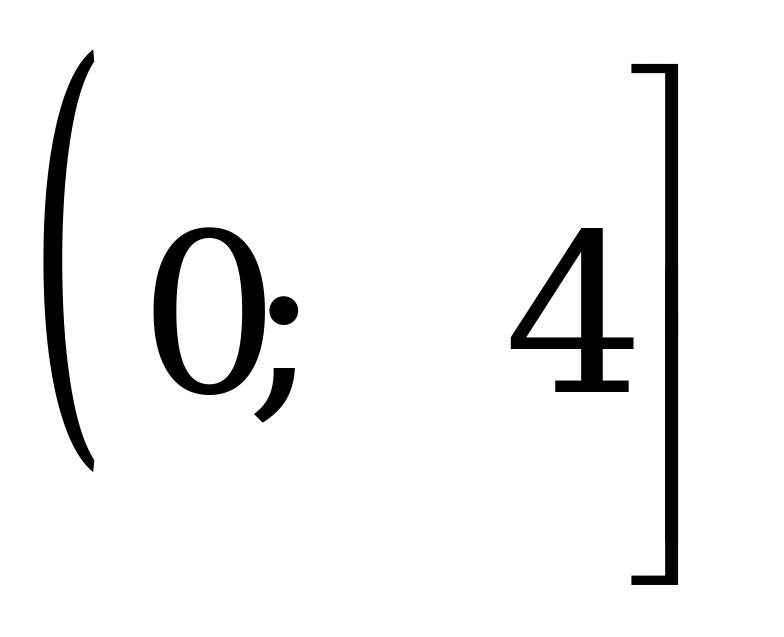
Найдите произведение корней уравнения
А) –480 B) –32 C) –24 D) –20 E) 480
Найдите произведение корней уравнения
Найдите сумму корней уравнения
Найдите сумму корней или корень, если он единственный, уравнения
Найдите сумму корней уравнения
Найдите наименьший корень уравнения
Найдите все значения параметра а, при которых графики функций 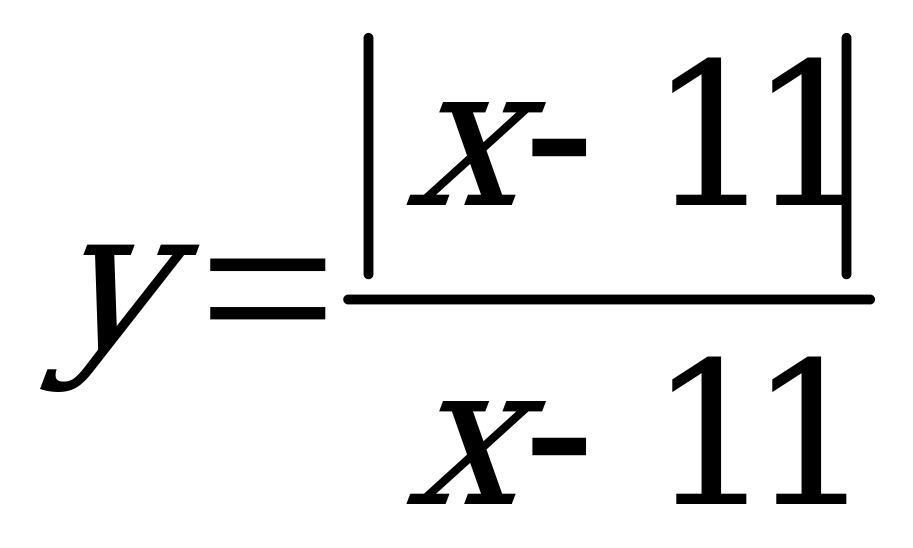
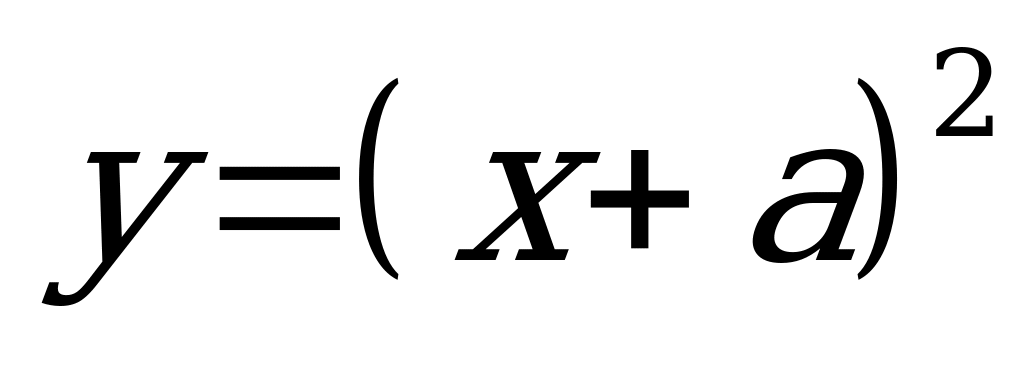
А) 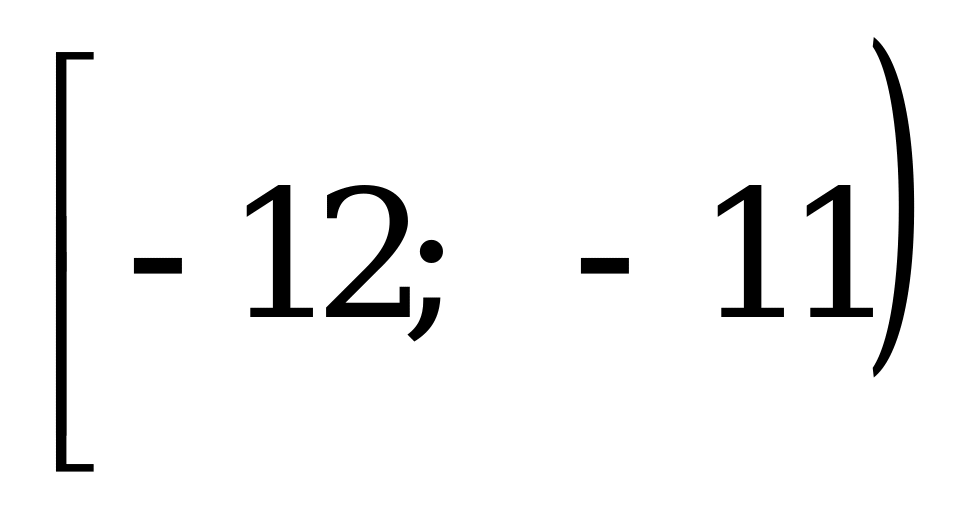
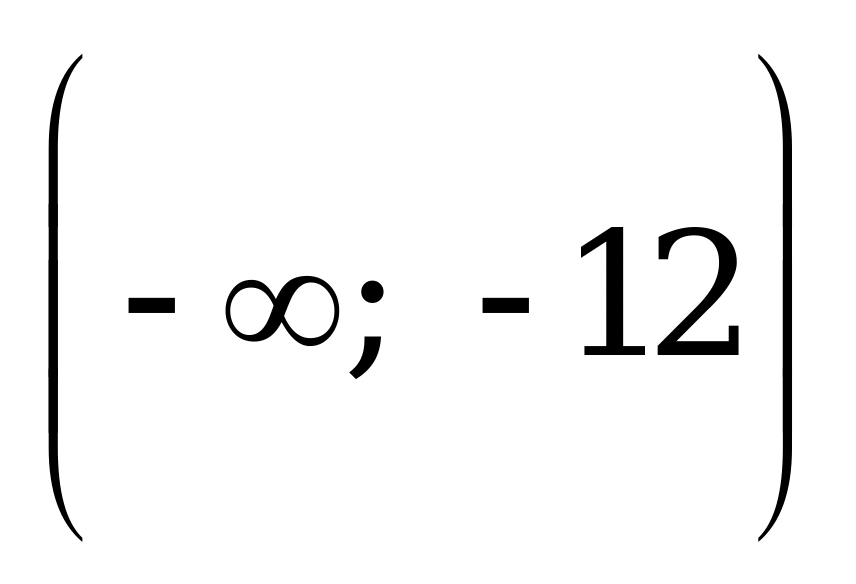
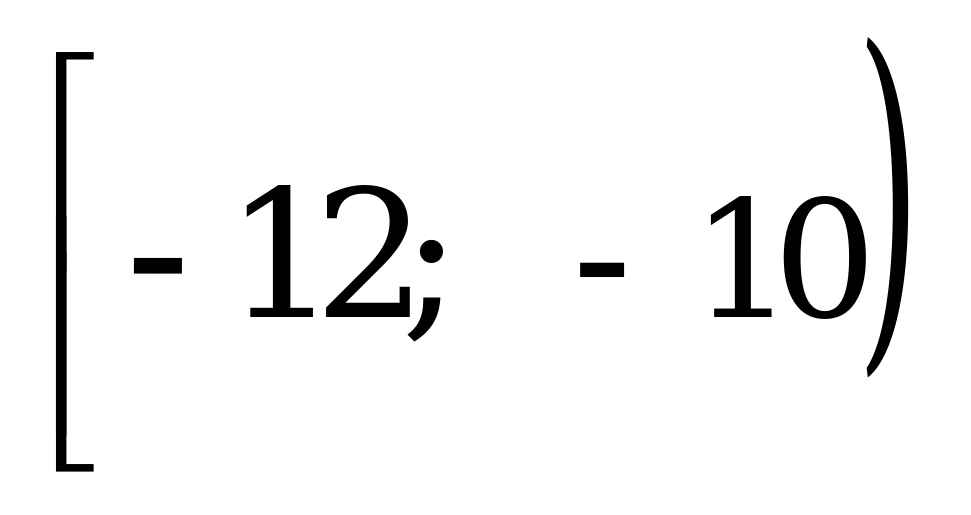
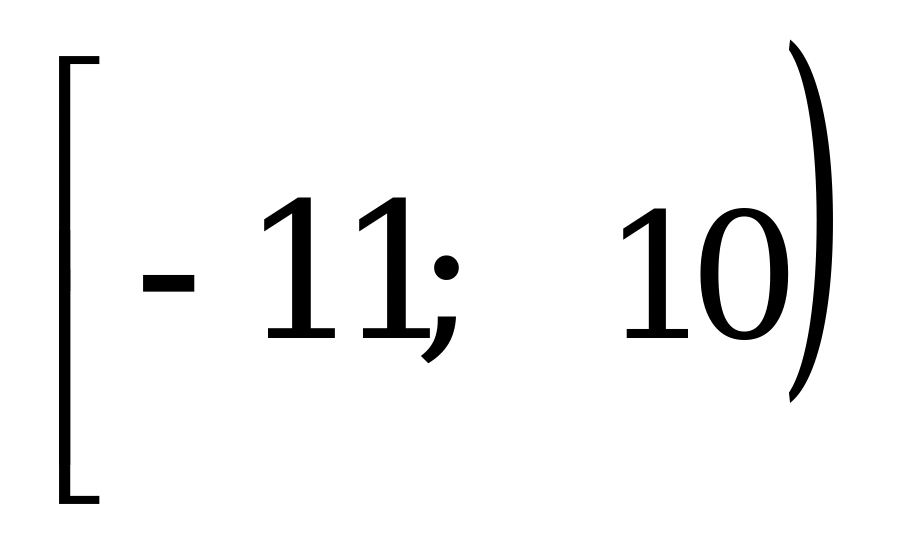
Укажите все значения параметра 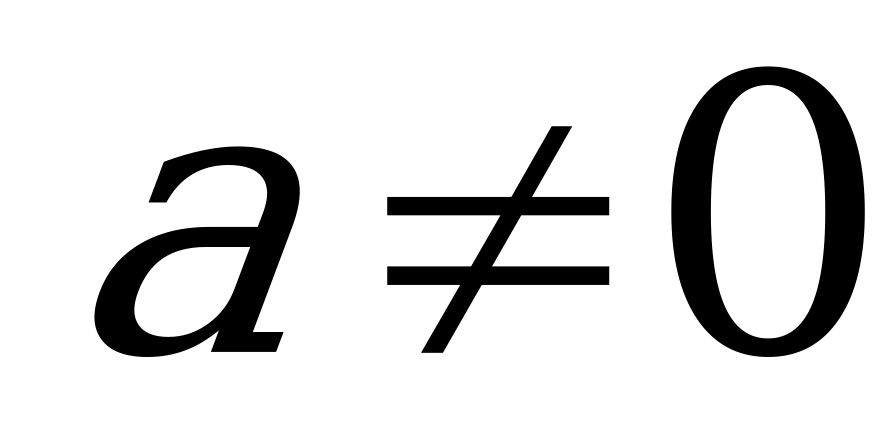
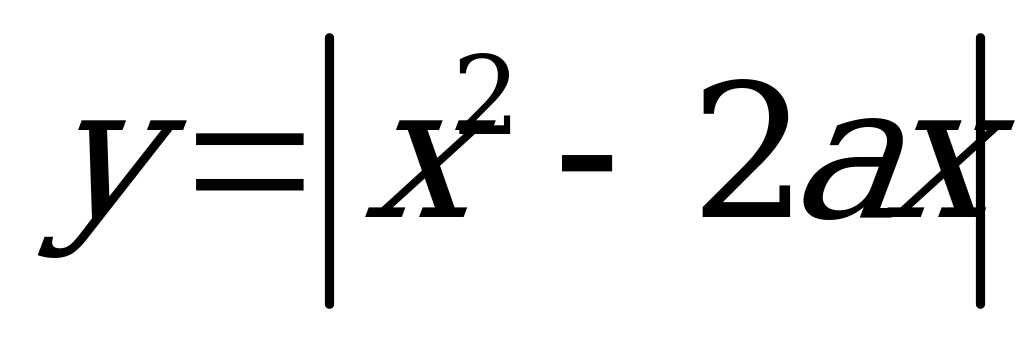
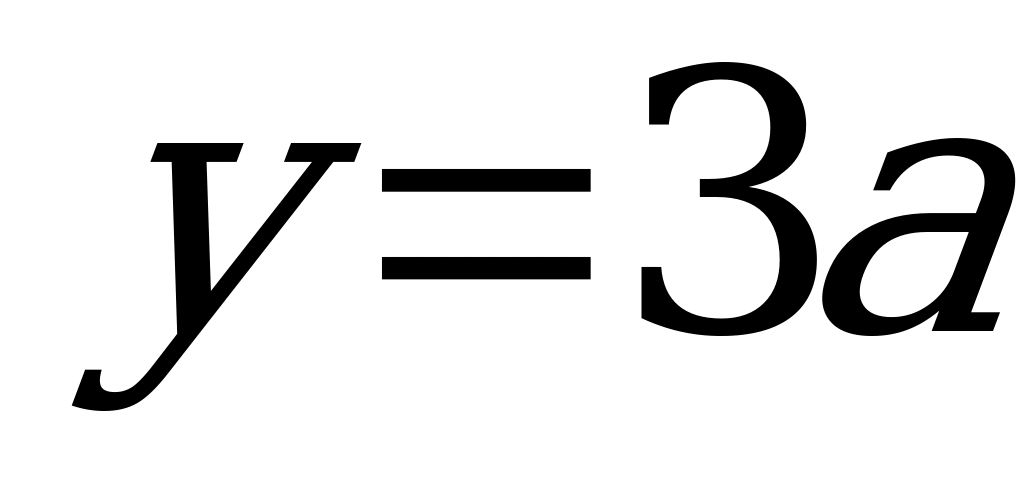
А) 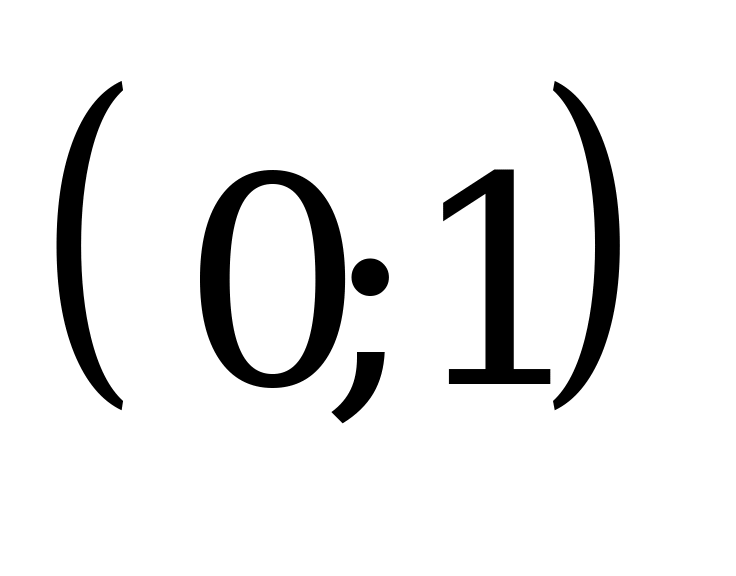
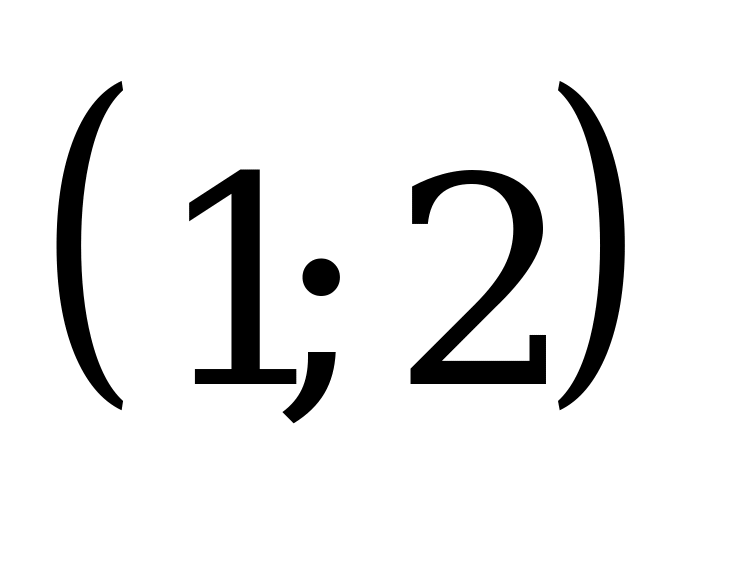
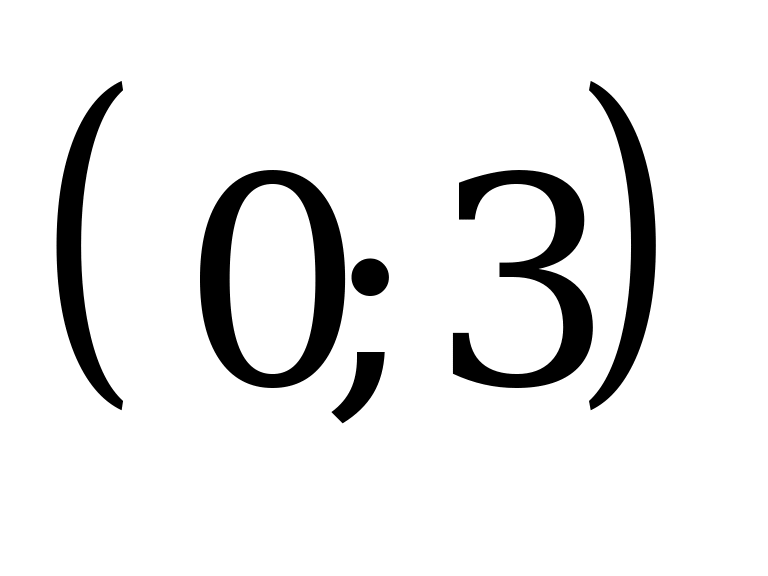

При каком значении параметра а уравнение 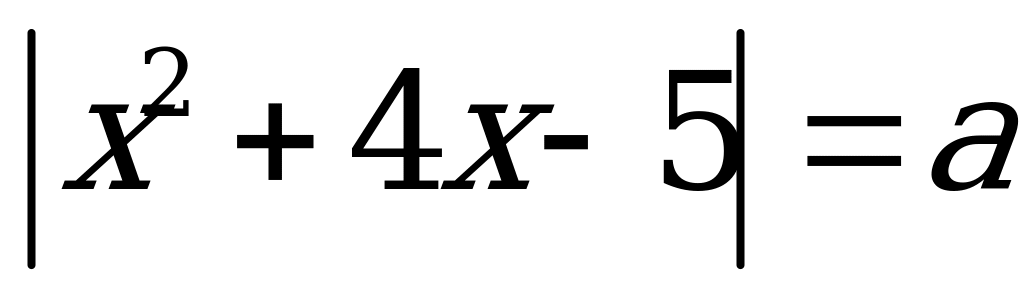
А) 4 B) 5 C) 8 D) 6 E) 9
Ответы теста «Уравнения с модулем»
Комментарии к некоторым задачам.
15. Предложим аналитическое решение этой задачи. Преобразуем первую функцию 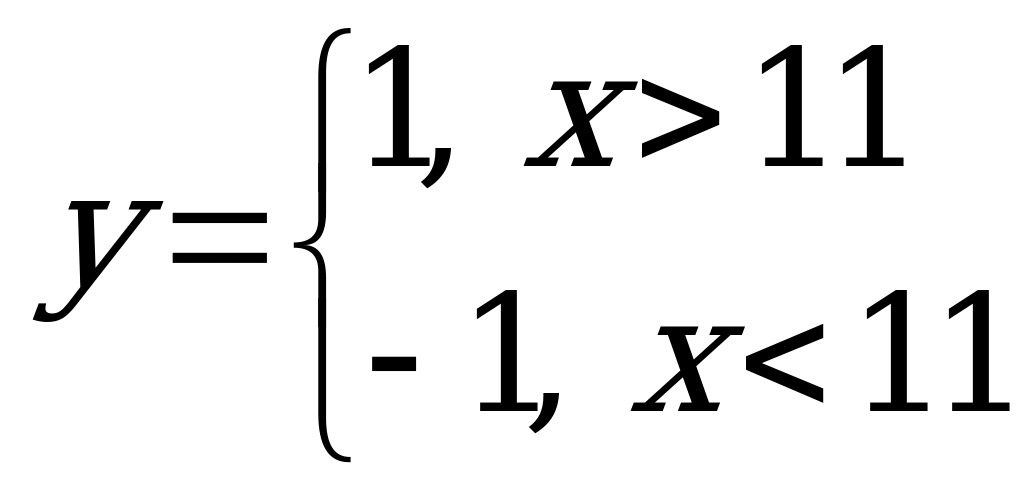
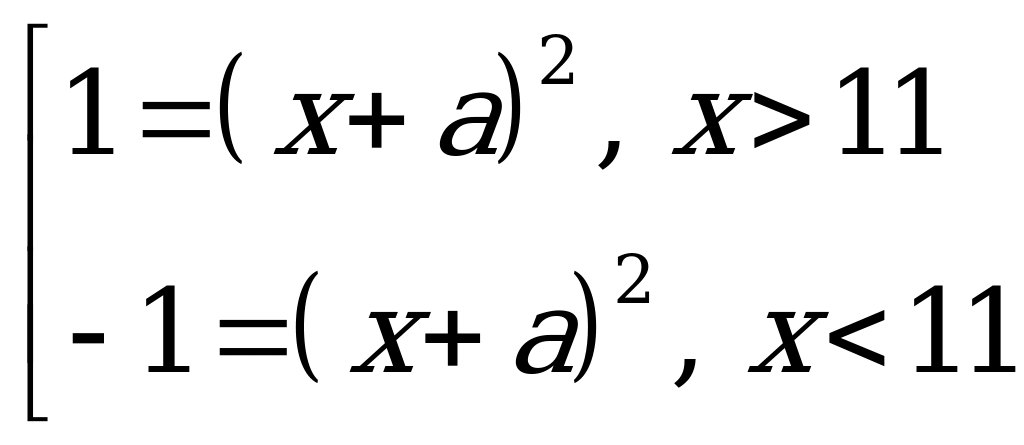
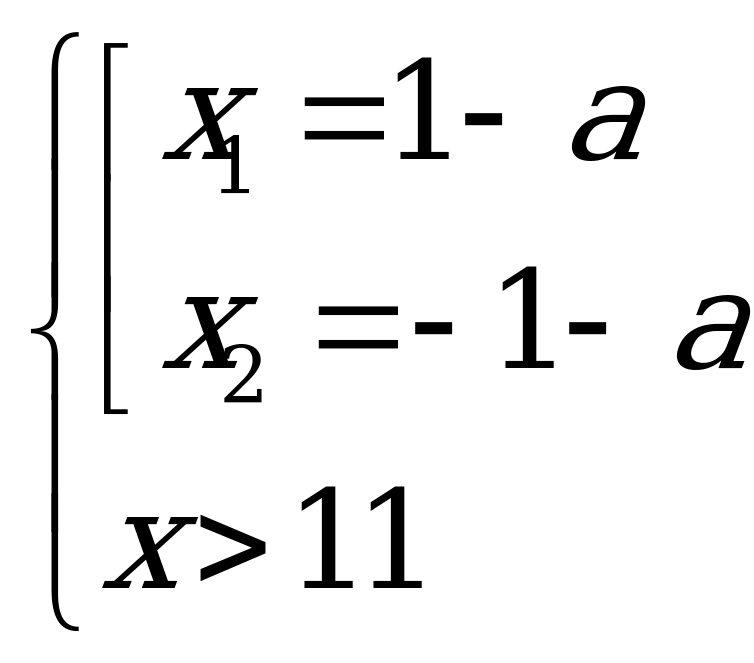
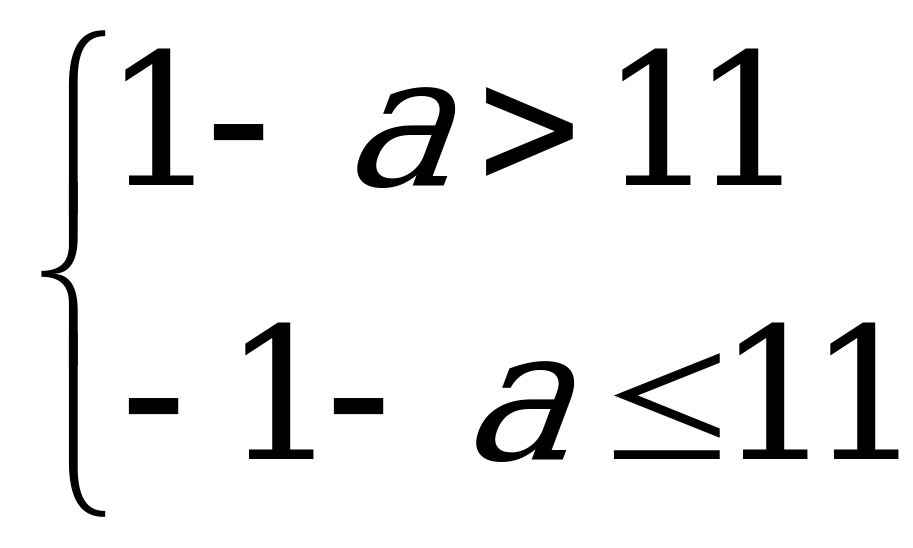
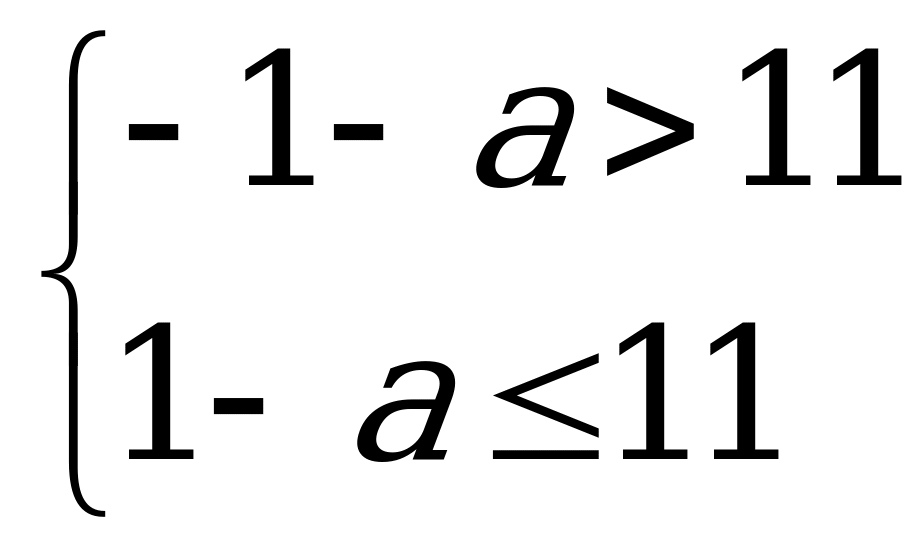
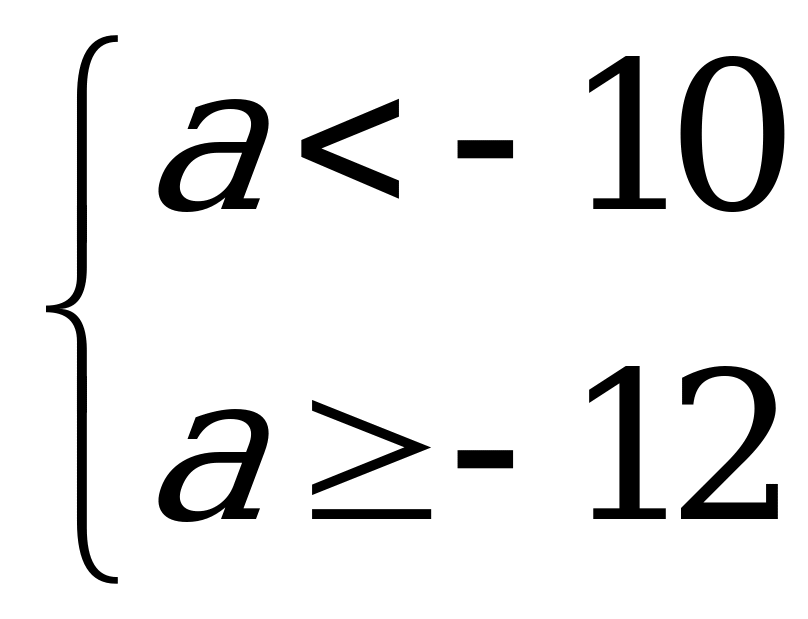
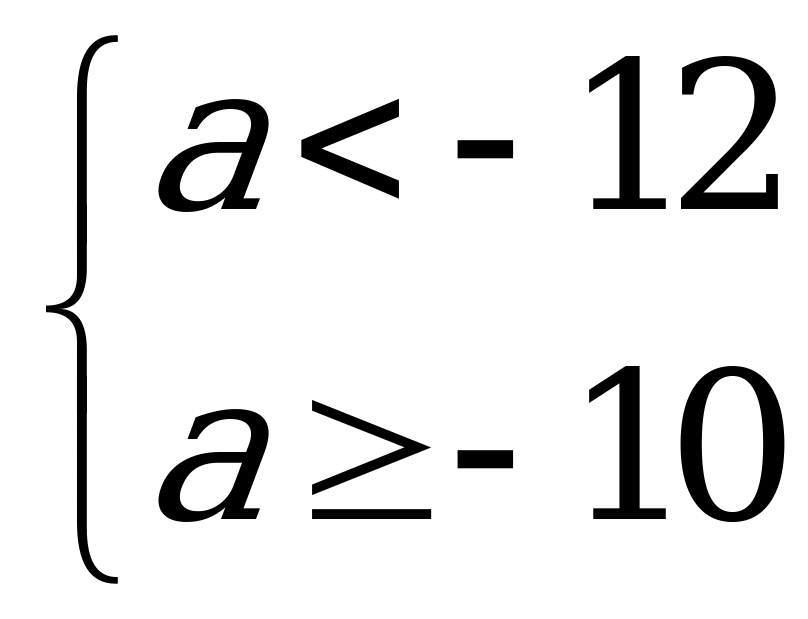
1 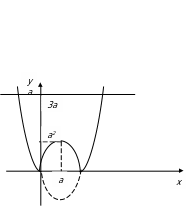
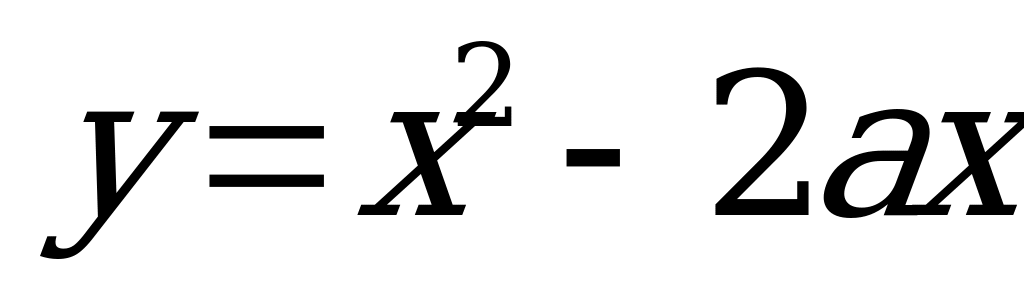
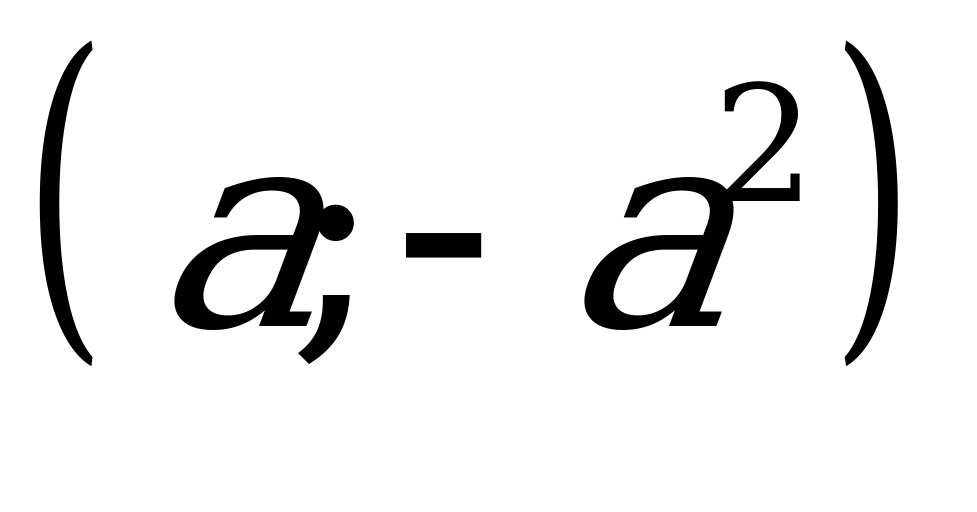
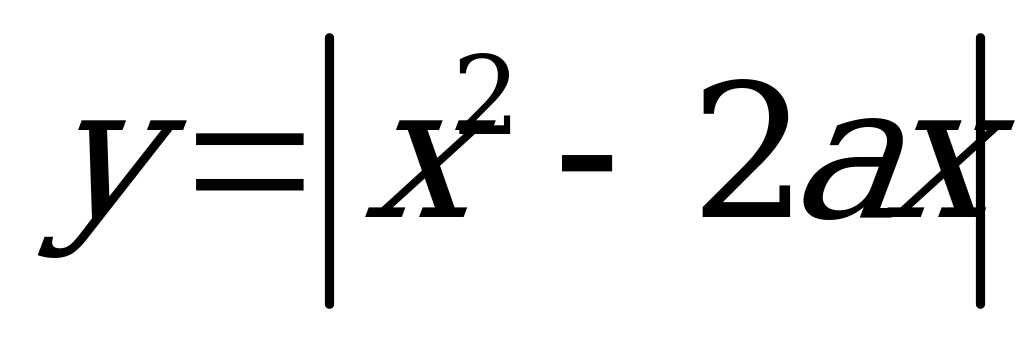
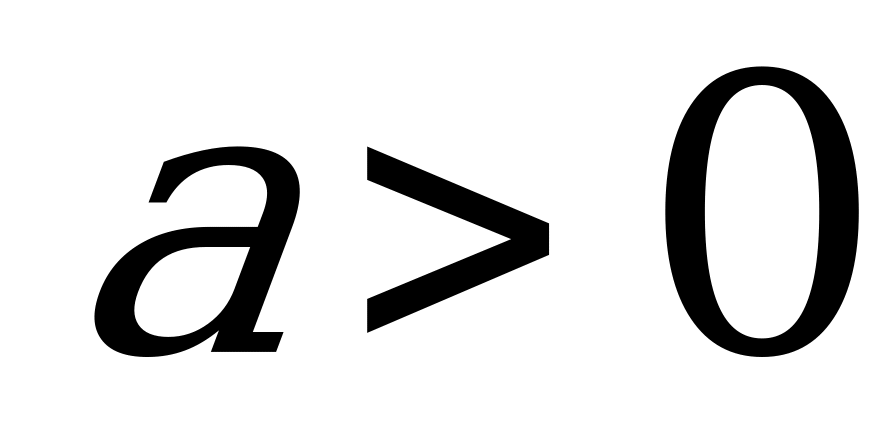
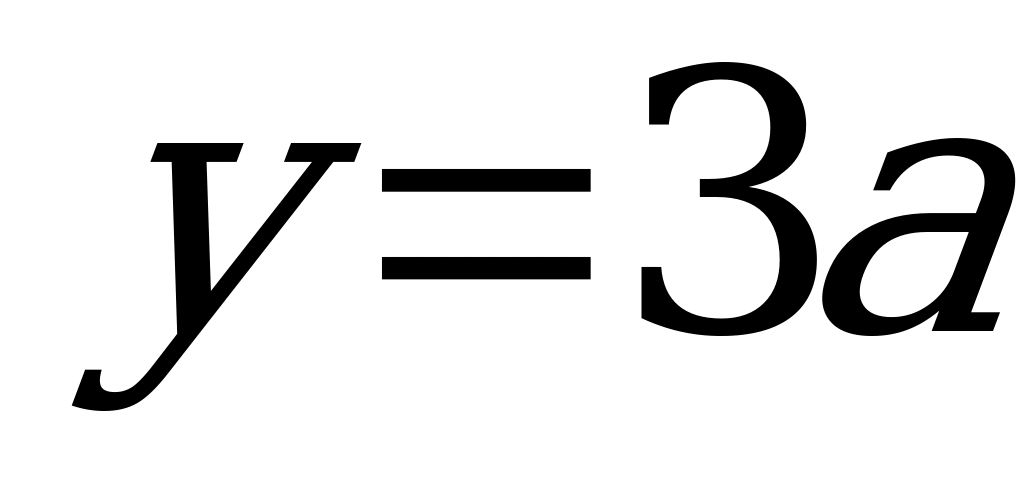
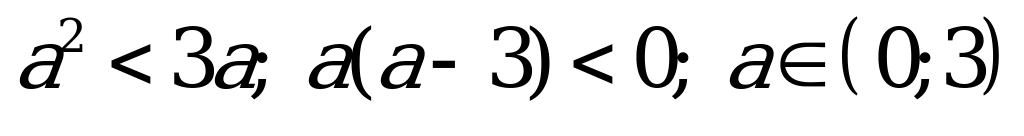
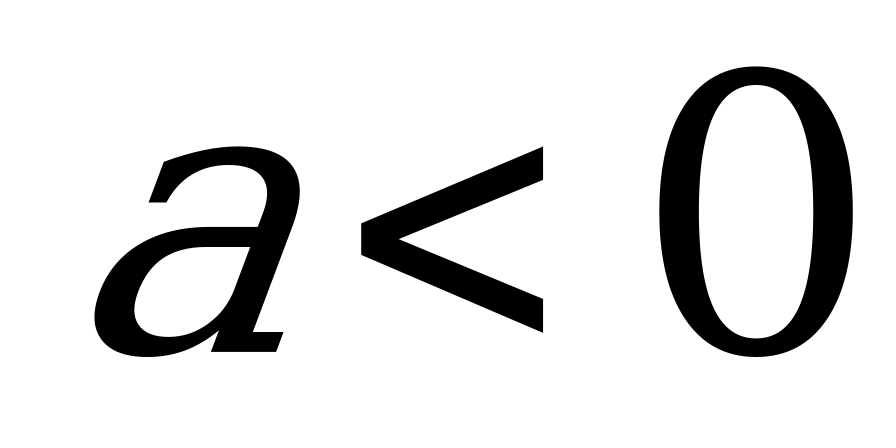
Неравенства с модулем
Рассмотрим теперь неравенства, в которых переменная стоит под знаком модуля. Начнем с простейших неравенств. Решим неравенство 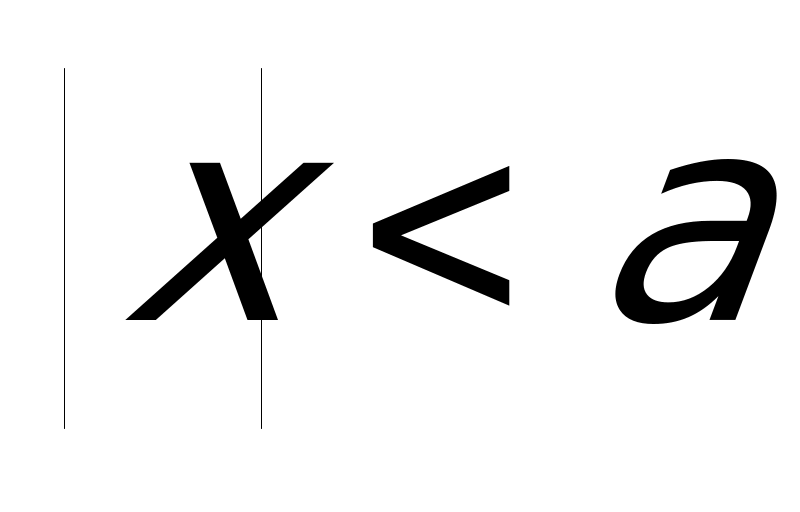
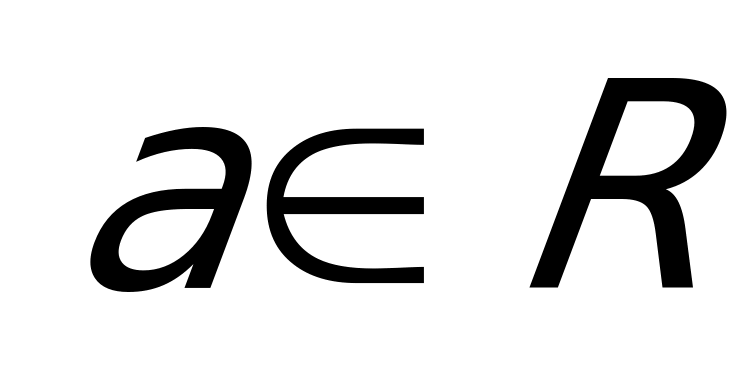
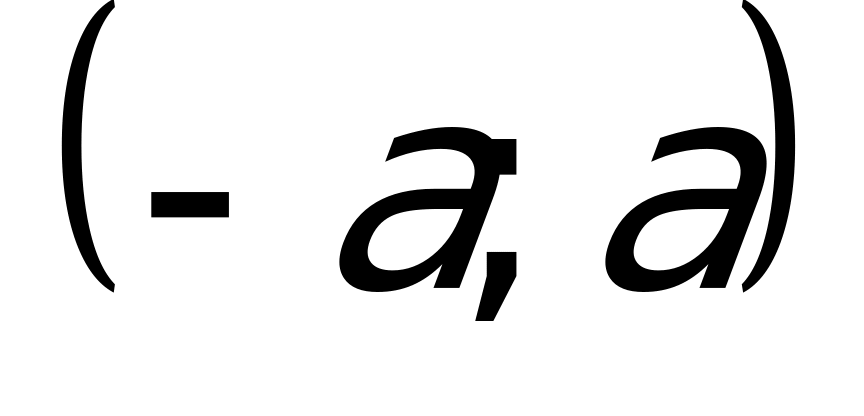
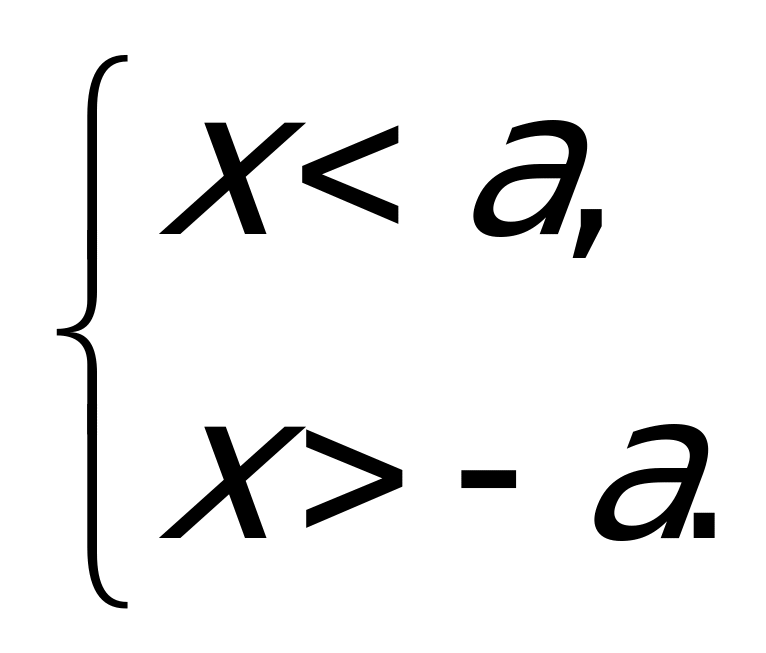
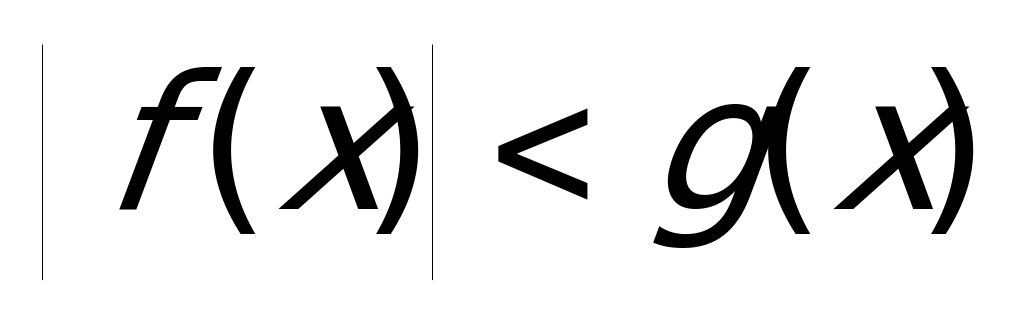
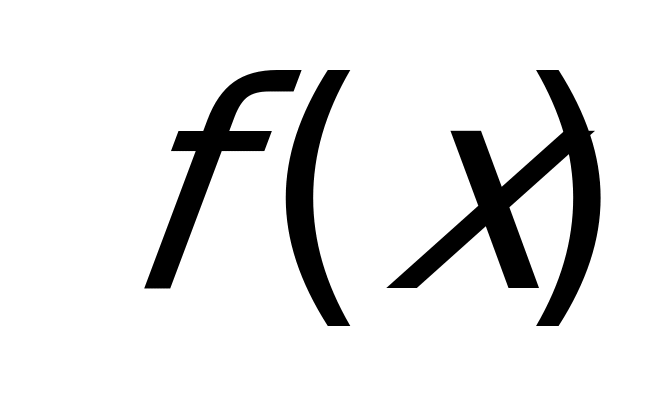
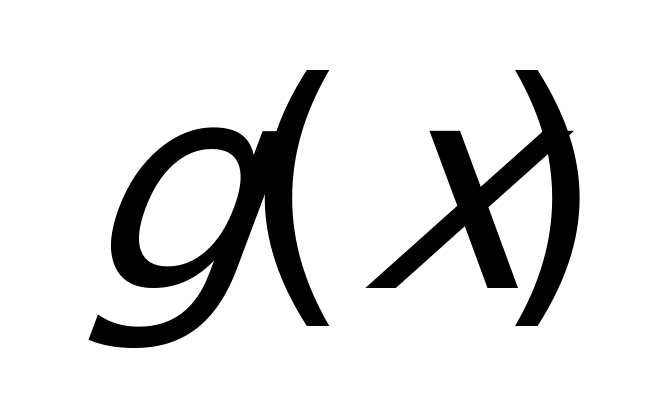
Для тех 
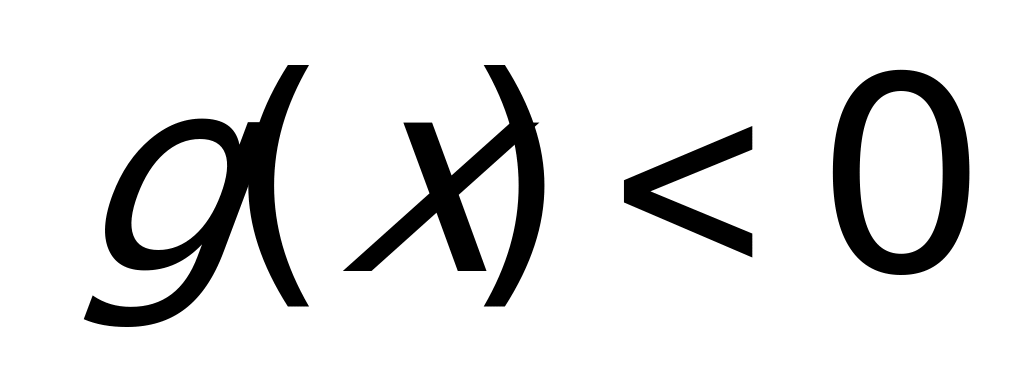
Пример 1а). Решите неравенство 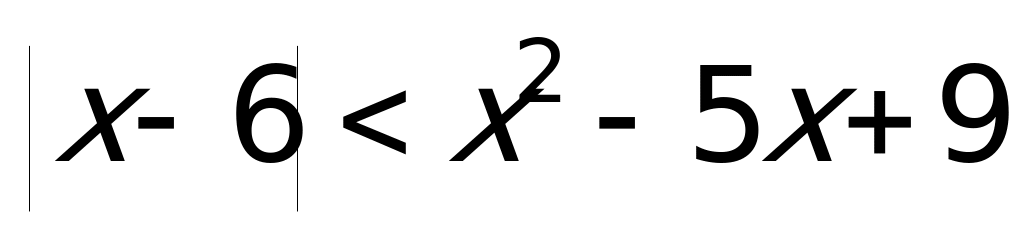
Решение: Данное неравенство равносильно системе:
Неравенство 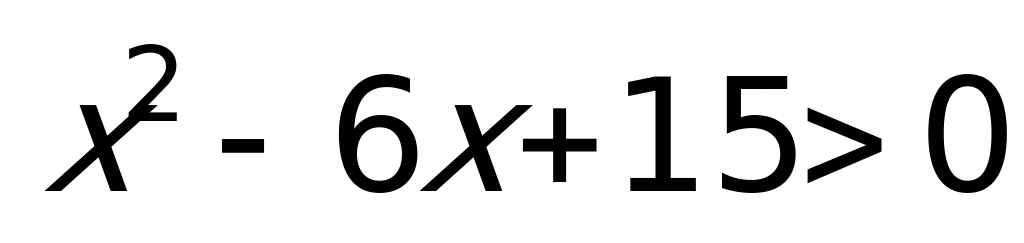
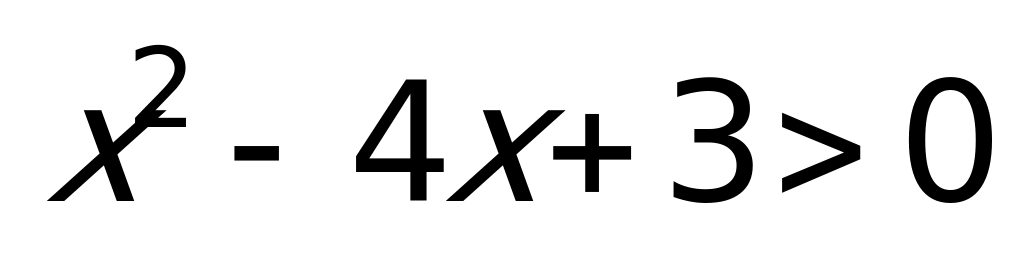
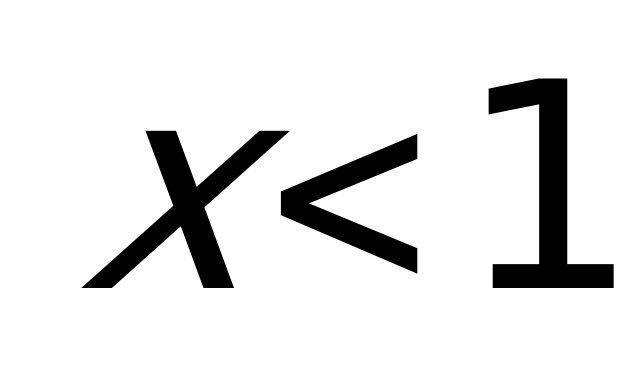
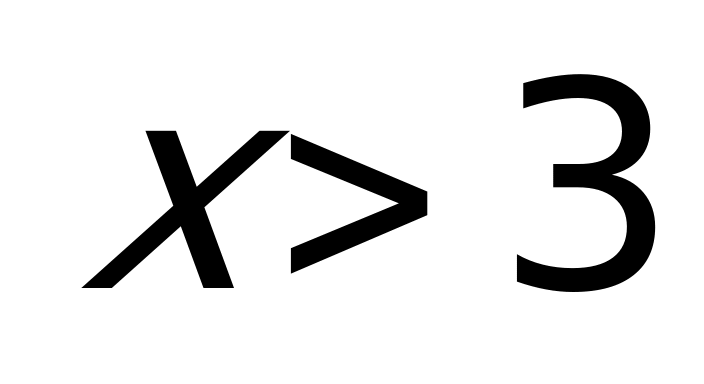
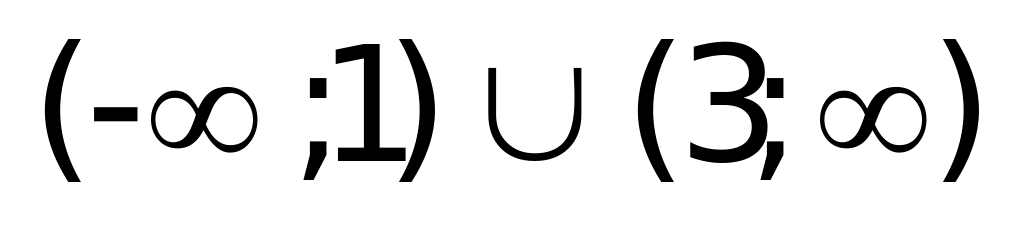
Ответ: 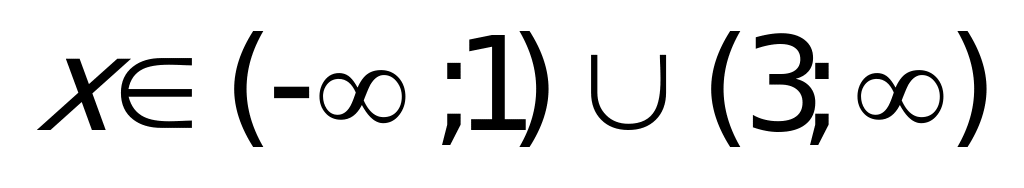
Пример 1б). Число целых решений неравенства 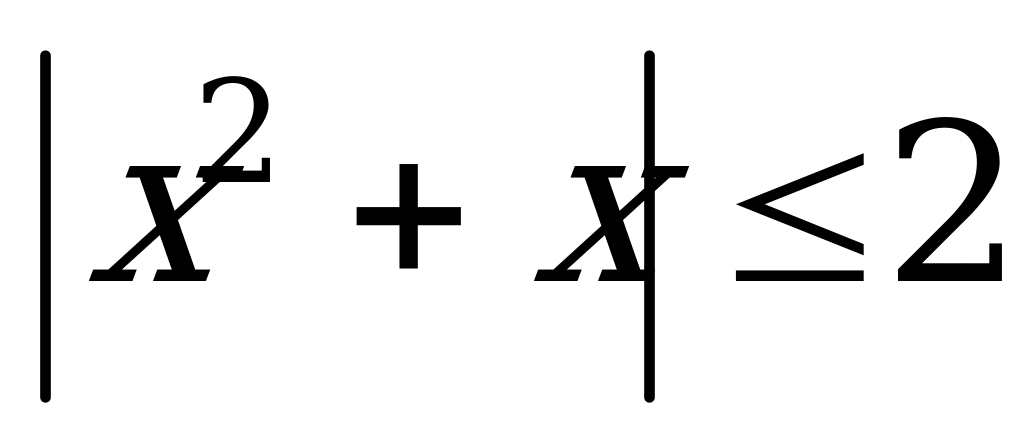
А) 4 B) 5 C) 3 D) 1 E) 2
Решение. Данное неравенство равносильно неравенству 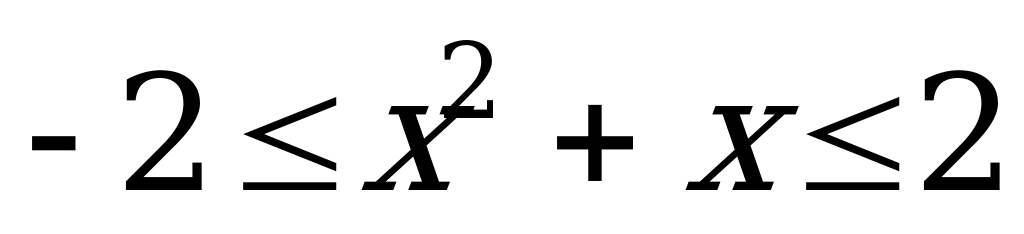
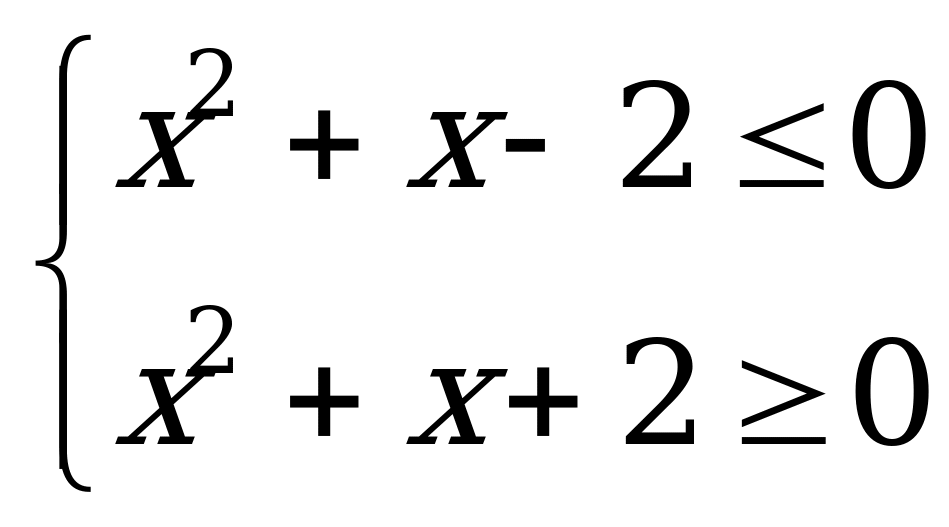
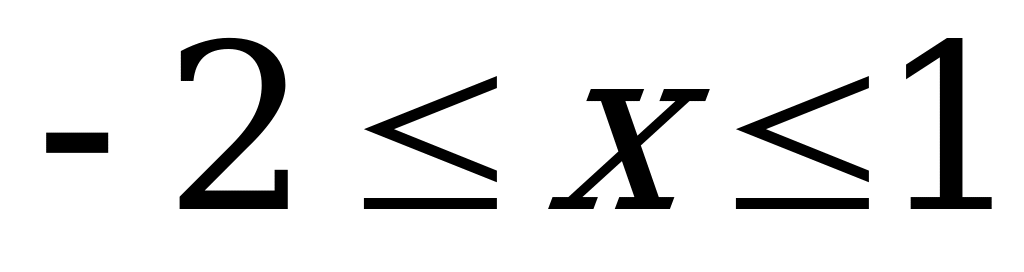
Пример 1в). Наибольшее целое решение неравенства 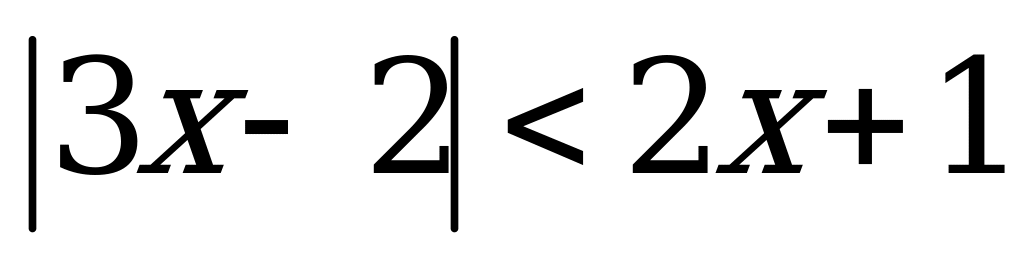
А) 4 B) 0 C) 3 D) 1 E) 2
Решение. Данное неравенство равносильно неравенству 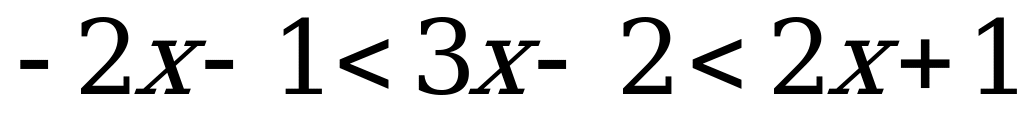
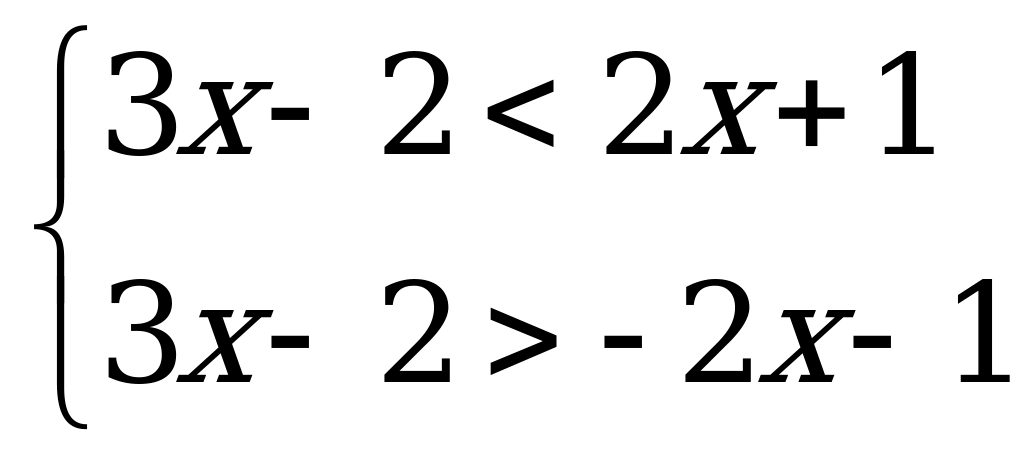
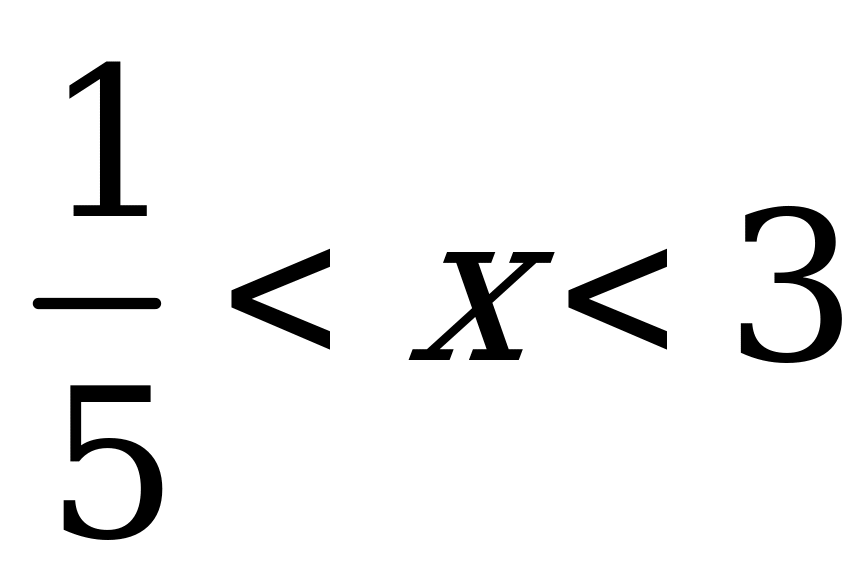
Теперь рассмотрим решение неравенства 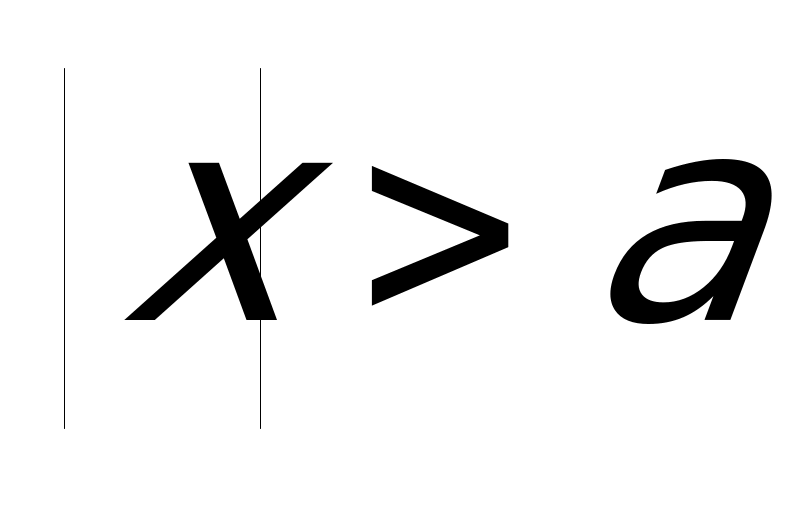
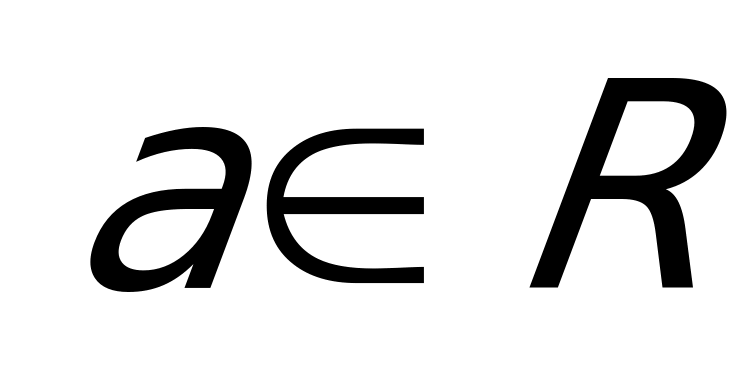
Из геометрического определения модуля следует, что решением данного неравенства является объединение интервалов 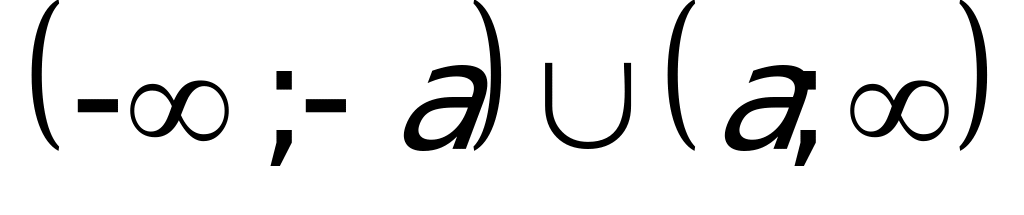
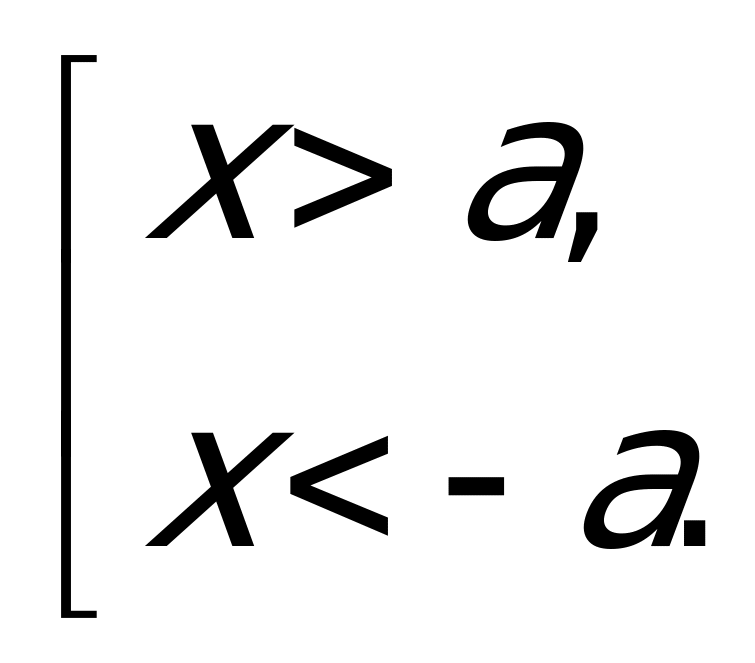
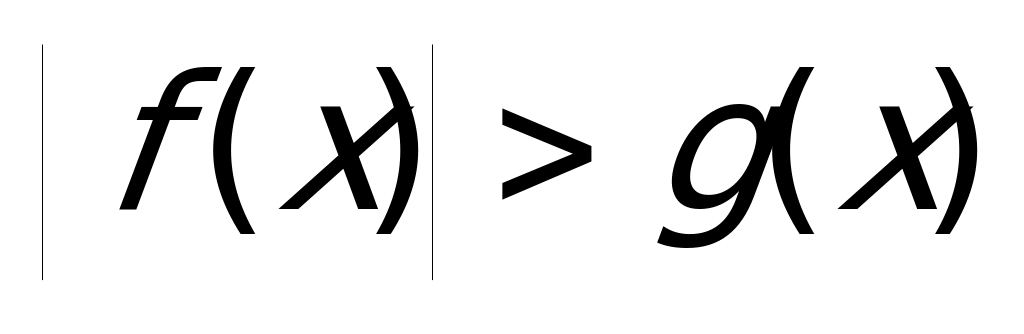
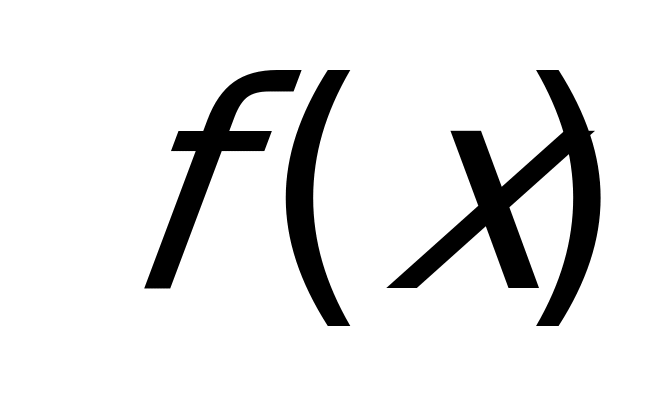
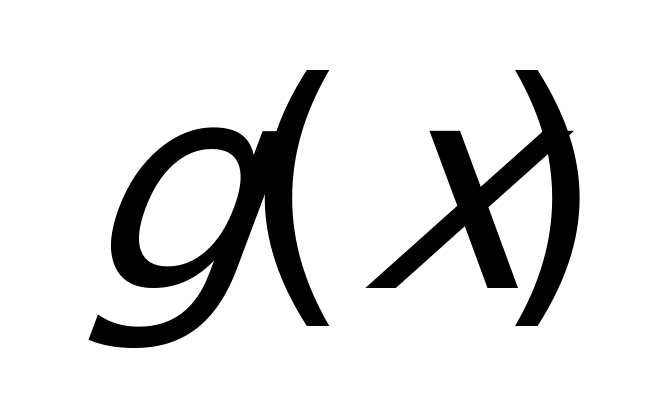
Пример 2а) Решите неравенство 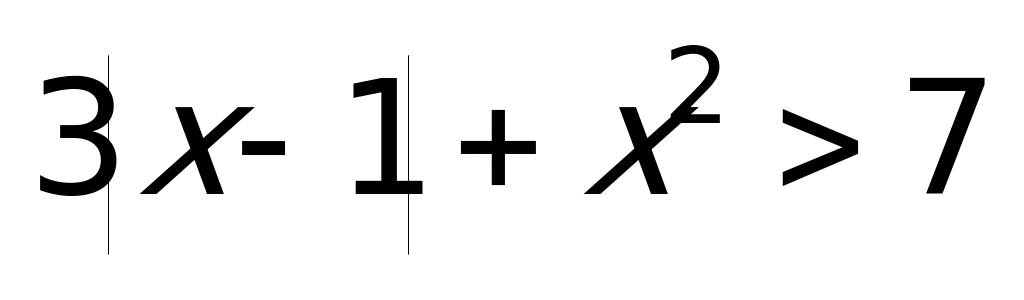
Решение: Данное неравенство можно переписать в виде: 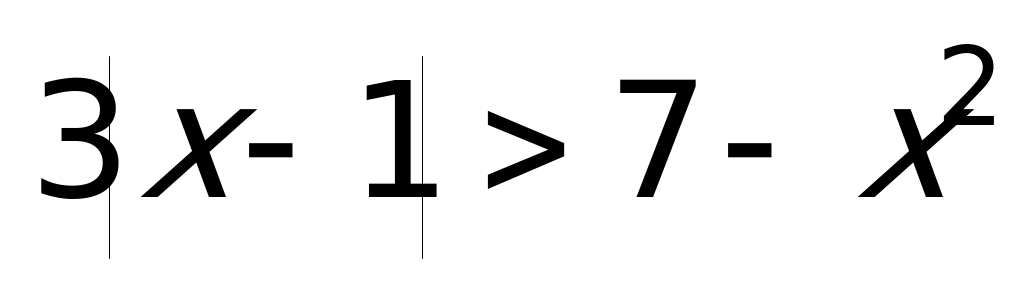
Поскольку 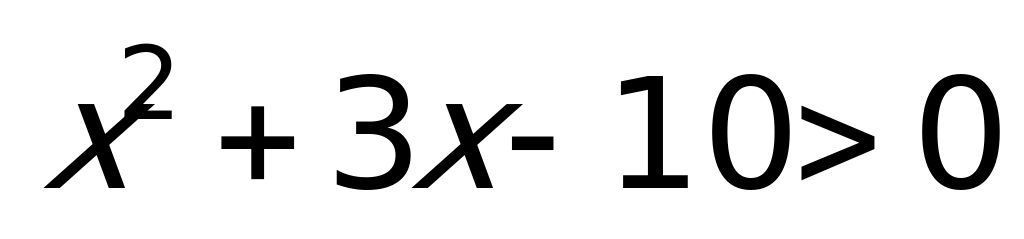
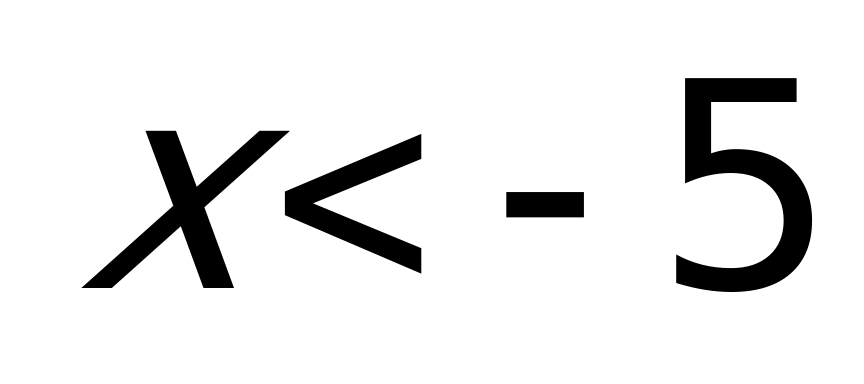
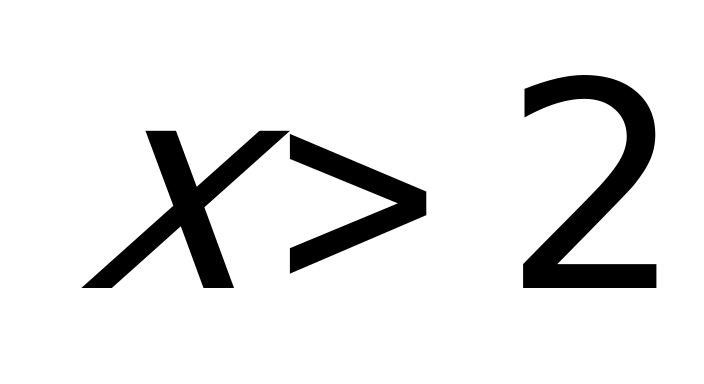
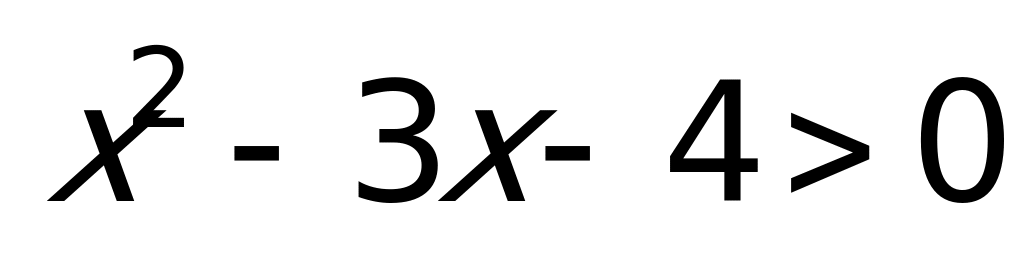
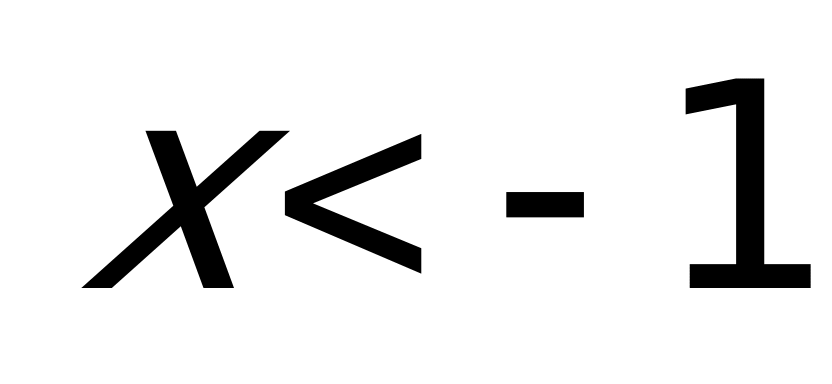
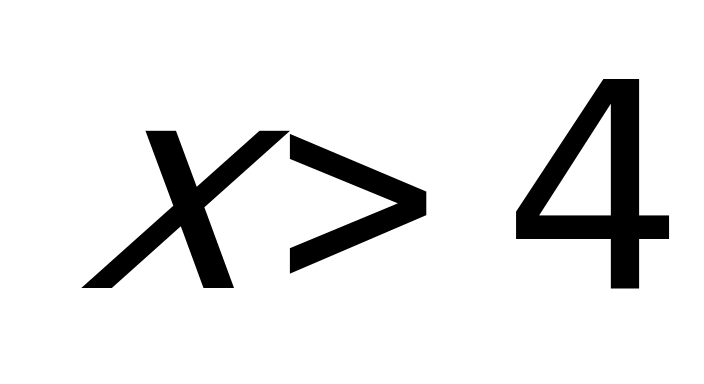
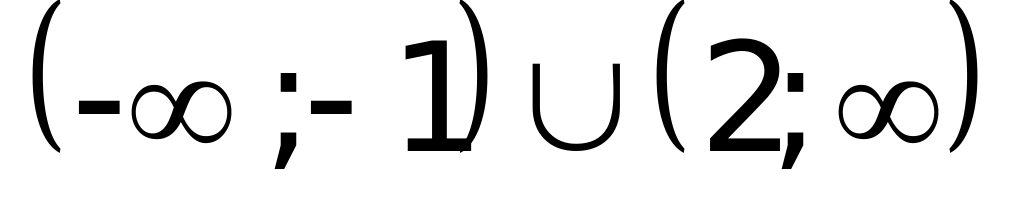
Ответ: 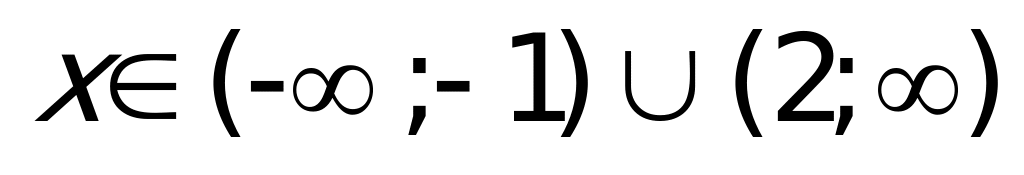
Пример 2б). Сумма всех целых решений неравенства 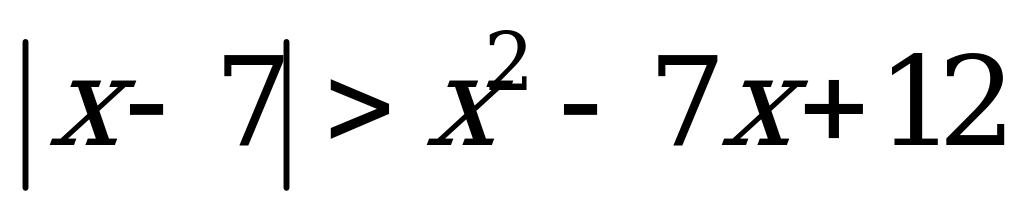
А) 14 B) 10 C) 8 D) 15 E) 9
Решение. Данное неравенство равносильно совокупности неравенств 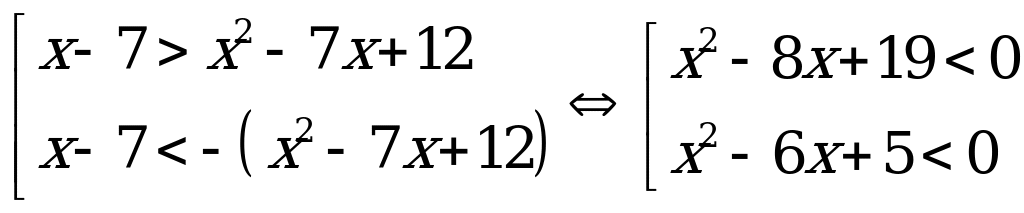
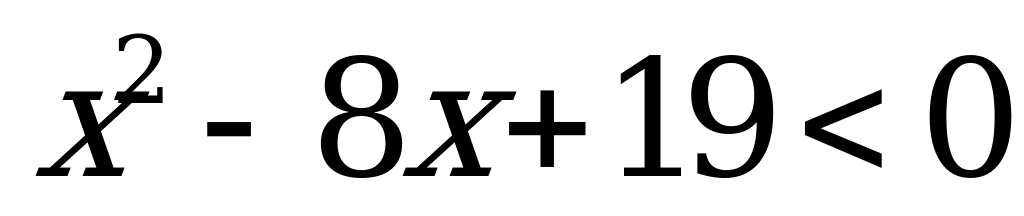
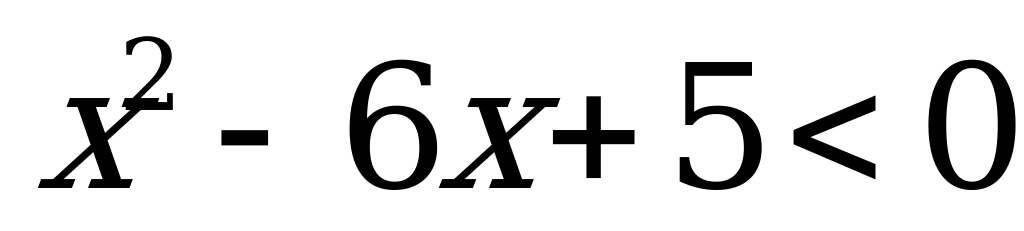
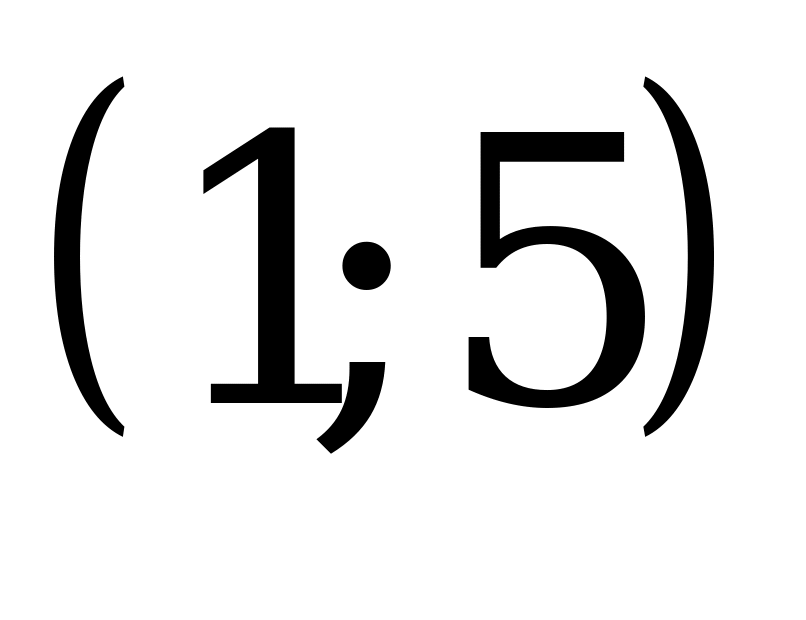
Пример 3а). Решите неравенство 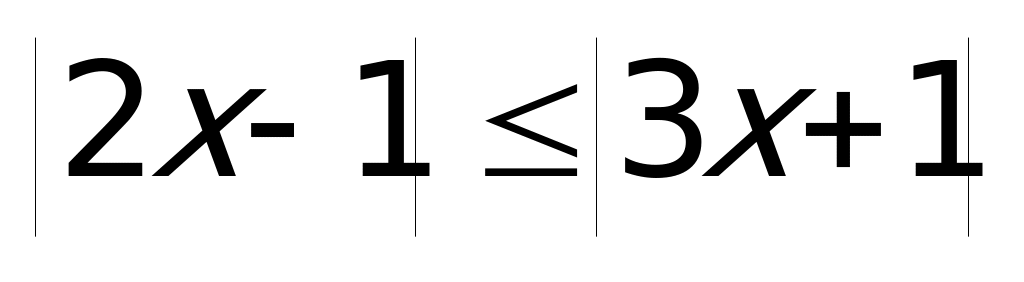
Решение: данное неравенство равносильно 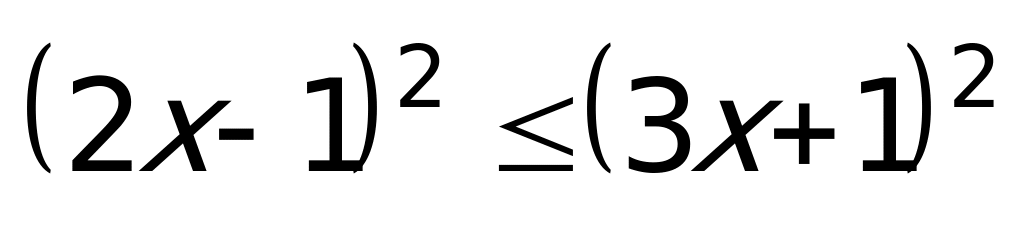
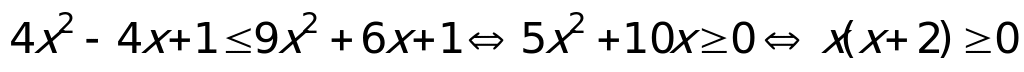
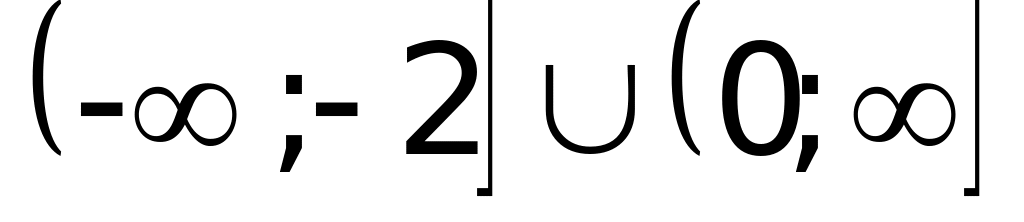
Ответ: 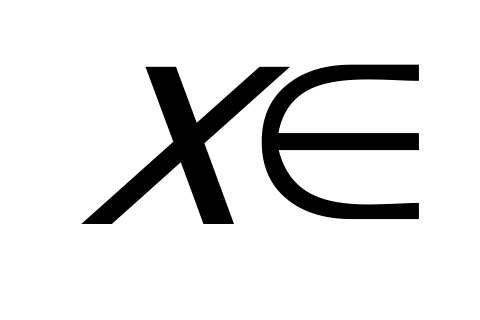
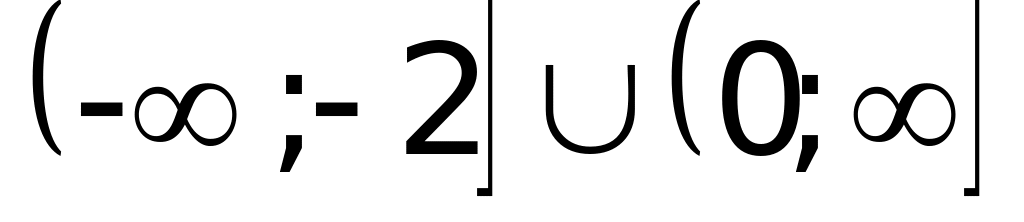
Пример 3б). Число целых решений неравенства 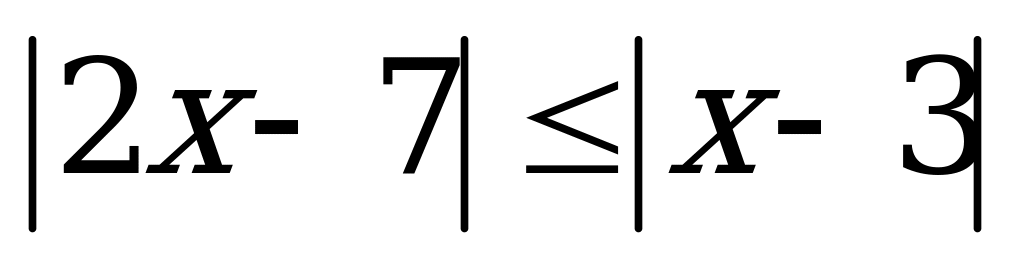
А) 4 B) 0 C) 3 D) 1 E) 2
Решение. Данное неравенство равносильно неравенству 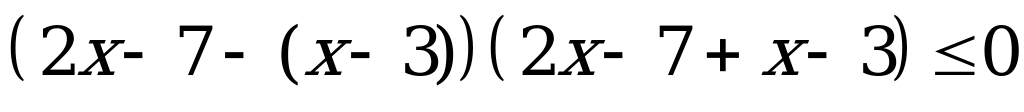
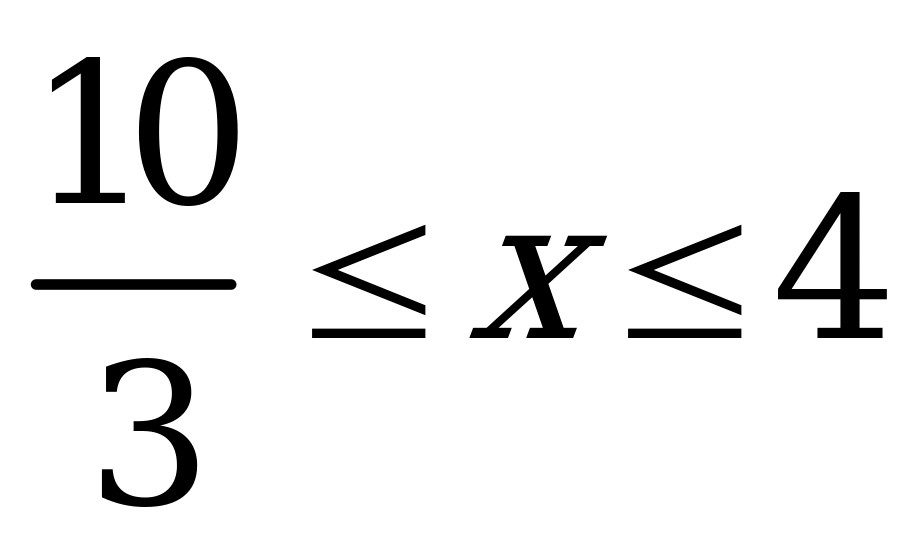
Неравенства, в которых под знаком модуля стоит несколько выражений, удобно решать аналогично методу разбиения на промежутки. Так же, как при решении подобных уравнений, находятся все точки смены знака каждого выражения, стоящего под знаком модуля, на каждом из полученных промежутков с учетом знаков указанных выражений модули раскрываются и решается полученное неравенство. Множество решений этого неравенства пересекается с рассматриваемым промежутком. Объединяя найденные множества, получаем множество всех решений исходного неравенства.
Пример 4а). Решите неравенство 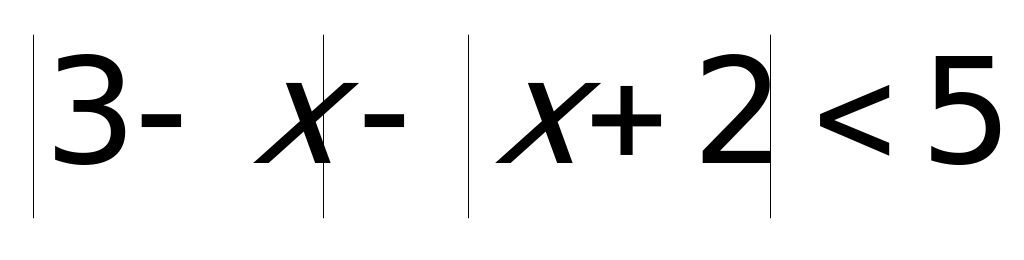
Решение: Так как 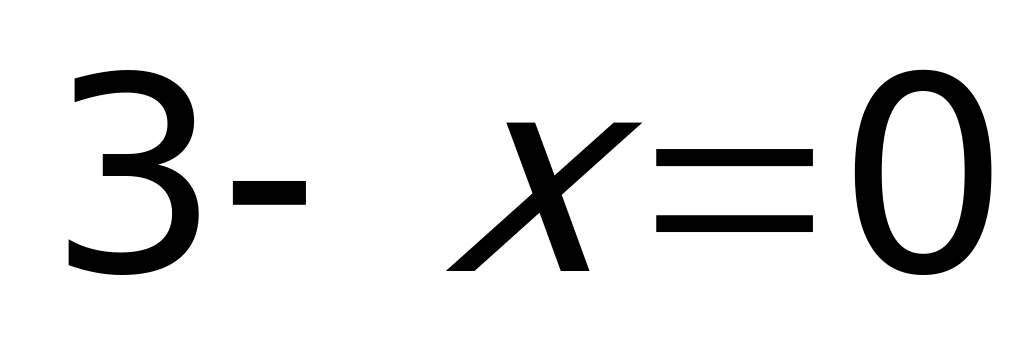
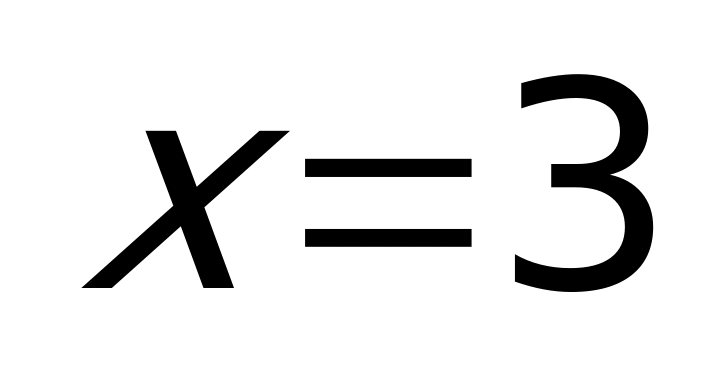
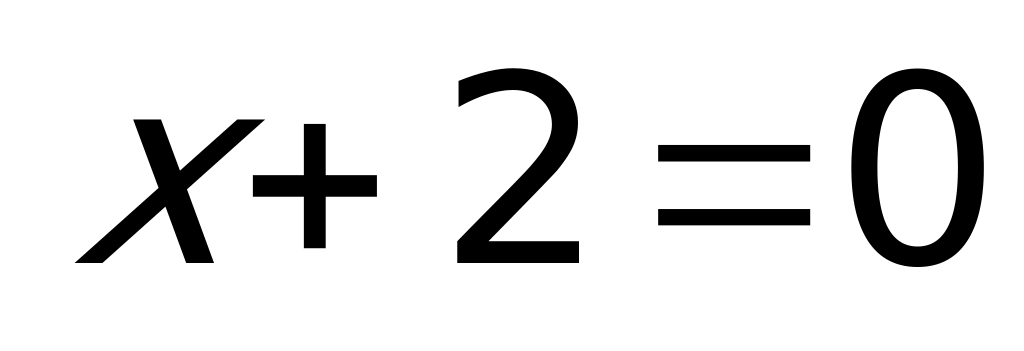
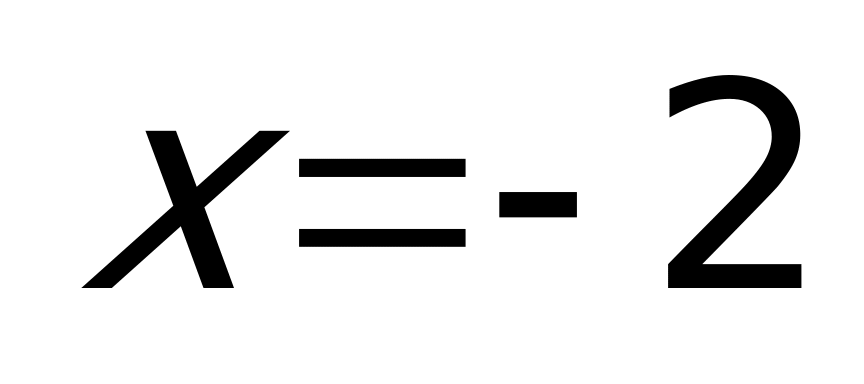
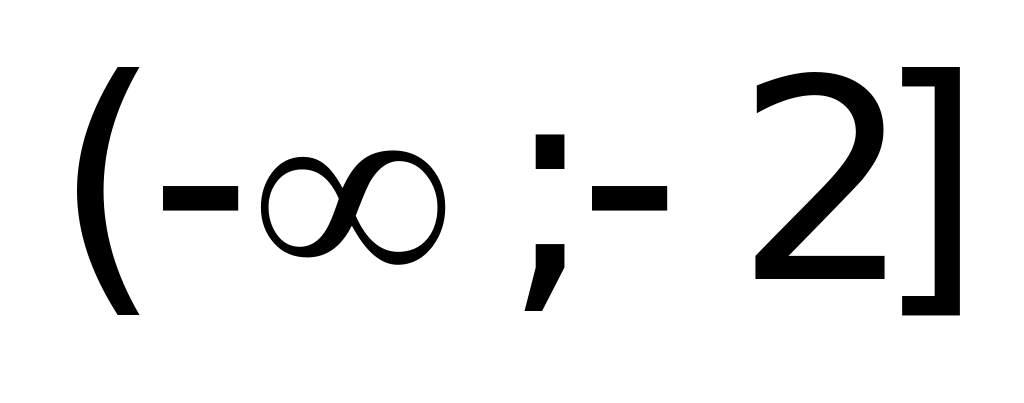

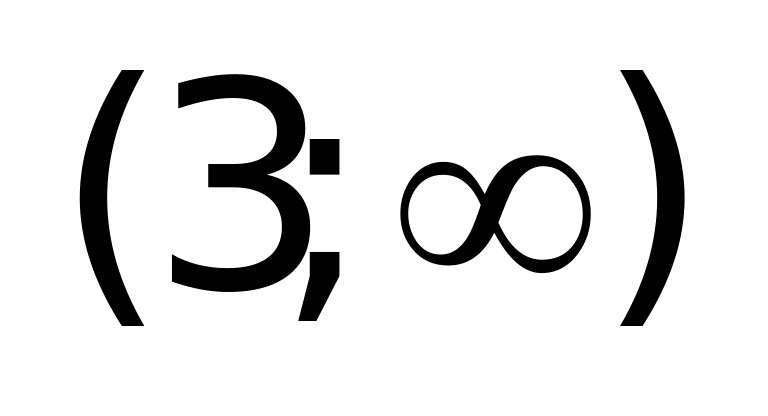
Тема урока: «Уравнения, содержащие переменную под знаком модуля»
Разделы: Математика
Тип урока: урок обобщения и систематизации учебного материала.
Форма урока: урок-практикум.
Класс: 11.
Предмет: алгебра и начала анализа.
Тема: “Уравнения, содержащие переменную под знаком модуля”
Цели:
- Актуализировать знания: модуль числа и свойства модуля; совершенствовать умение при решении уравнений, содержащих переменную под знаком модуля, применять методы: раскрытие модуля по определению; возведение обеих частей уравнения в квадрат; метод разбиения на промежутки.
- Развивать интеллектуально-логические умения и математические способности;
- Воспитывать адаптивность к современным условиям обучения, воспитывать личность, интегрированную в современное общество.
I. Организационный момент.
II. Мотивация деятельности учащихся.
Сообщение целей и задач урока. Принятие учащимися целей урока.
III. Актуализация опорных знаний.
1. Определение модуля. Модулем (абсолютной величиной) действительного числа х называется само это число, если х > 0, и противоположное ему число –х, если х 0.
-|x| 3 – 15x 2 + x + 7.
По определению модуля
Уравнение |x – 7| = x 3 – 15x 2 + x + 7 равносильно следующей совокупности двух смешанных систем:
Ответ: 0;
Уравнение вида |f(x)| = |g(x)|.
|x 5 -6x 2 +9x-6| = |x 5 -2x 3 +6x 2 -13x+6|.
|x 5 -6x 2 +9x-6| > 0 и |x 5 -2x 3 +6x 2 -13x+6| > 0.
Так как обе части уравнения неотрицательны, то данное уравнение равносильно совокупности двух уравнений:
Решив каждое из уравнений, получим:
х = 0; х = ± 
Ответ: 0; ± 
|2x + 1| + |5 — 3x| + 1 — 4x = 0.
1. По определению модуля

2. Hайдём критические точки:
2х + 1 = 0; 5 — 3х = 0.
3. Hули функции разбивают числовую ось на промежутки.
4. Решим уравнение на каждом из промежутков:
Уравнение, записанное без знака модуля на промежутках х 

Ответ: 
Ученик может выбрать любой из трёх уровней примеров. Первый уровень оценивается оценкой “3”, второй “4”, третий “5”. Решение в тетрадях с последующим объяснением своего решения в группах. Наиболее сложные задания решаются у доски. Решения проверяются и записываются в тетрадях. Оставшиеся задания выполняются дома.
V. Самостоятельная работа.
Самостоятельная письменная работа по вариантам
на отдельных листах с последующей сдачей учителю вместе с диагностическими листами
Вариант 2
А
x 2 +|x-1|-5=0. (МФТИ 1999)
Б
|2x+8|-|x-5|=12 (МГУ 2000)
В
|6x 3 -2x 2 +4x-33|=10x-35 (МФТИ)
Методы решения уравнений, содержащих переменную под знаком модуля.
Алгоритм решения уравнений, содержащих переменную под знаком модуля.
VII. Домашнее задание.
Решить три уравнения различного уровня.
Индивидуальные задания.
2. | | 3х + 2| — 5х| = 14;
3. | 2 — | 3х — 1| | = х 2 + 1;
4. | 3х – 1| + | 2х — 4| = | х 2 — 1| + 4;
5. | х + 2| — | 3х — 4| + | 2х + 7| — = | х + 5|.
http://multiurok.ru/index.php/files/proektnaia-rabota-9-klass-reshenie-uravnenii-i-ner.html
http://urok.1sept.ru/articles/313822