Построение графика функции методом дифференциального исчисления
Правила ввода функции
- Примеры
≡ x^2/(x+2)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
Пример №1 . Провести полное исследование функции 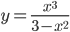
1) Функция определена всюду, кроме точек 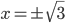
2) Функция нечетная, так как f(-x) = -f(x) , и, следовательно, ее график симметричен относительно начала координат. Поэтому ограничимся исследованием только для 0 ≤ x ≤ +∞.
3) Функция не периодическая.
4) Так как y=0 только при x=0, то пересечение с осями координат происходит только в начале координат.
5) Функция имеет разрыв второго рода в точке 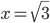
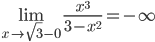
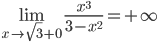
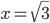
6) Находим 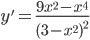
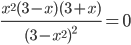
В окрестности точки x3=3 имеет: y’>0 при x 3, следовательно, в точке x3 функция имеет максимум, ymax(3)=-9/2. Найти первую производную функции
7) Находим 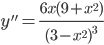

8) Выясним вопрос об асимптотах.
Наличие вертикальной асимптоты 

Найдем наклонные асимптоты: 

9) Теперь, используя полученные данные, строим чертеж:

Пример №2 . Построить график функции 
Решение.
1. Область определения функции D(y) = (-∞;0)U(0;∞).
2. Функция не является четной или нечетной.
3. Найдем точки пересечения графика с осью ОХ; имеем 

4. Точки разрыва x=0 , причем 
Найдем наклонные асимптоты: 

Наклонная асимптота имеет уравнение y=x .
5. Найдем экстремум функции и интервалы возрастания и убывания. Имеем 
6. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба. Так как y’’>0 (x≠0), то график функции всюду вогнут. Точек перегиба кривая не имеет.
Строим график функции.
Применение производной для решения нелинейных уравнений и неравенств
п.1. Количество корней кубического уравнения
Кубическое уравнение $$ ax^3+bx^2+cx+d=0 $$ на множестве действительных чисел может иметь один, два или три корня.
С помощью производной можно быстро ответить на вопрос, сколько корней имеет данное уравнение. \begin
Если две точки экстремума найдены, но \(f(x_1)\cdot f(x_2)=0\), уравнение имеет два корня.
Во всех остальных случаях – у исходного уравнения 1 корень.
Пример 1. Сколько корней имеют уравнения:
| 1) \(x^3+3x^2-4=0\) \(b^2-3ac=9\gt 0 (c=0) \) \(f(x)=x^3+3x^2-4 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-4,\ f(x_2)=0 \) \(f(x_1)\cdot f(x_2)=0\Rightarrow\) два корня  | 2) \(x^3+3x^2-1=0\) \(b^2-3ac=9\gt 0 \) \(f(x)=x^3+3x^2-1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=-1,\ f(x_2)=3 \) \(f(x_1)\cdot f(x_2)\lt 0\Rightarrow\) три корня  |
| 3) \(x^3+3x^2+1=0\) \(b^2-3ac=9\gt 0\) \(f(x)=x^3+3x^2+1 \) \(f'(x)=3x^2+6x=3x(x+2) \) \(x_1=0,\ x_2=-2 \) \(f(x_1)=1,\ f(x_2)=5 \) \(f(x_1)\cdot f(x_2)\gt 0\Rightarrow\) один корень  | 4) \(x^3+x^2+x+3=0\) \(b^2-3ac=1-3\lt 0 \) Один корень  |
п.2. Количество корней произвольного уравнения
Задачи на подсчет количества корней решаются с помощью построения графиков при полном или частичном исследовании функций.
Пример 2. а) Найдите число корней уравнения \(\frac 1x+\frac<1>
б) Найдите число корней уравнения \(\frac 1x+\frac<1>
Построим график функции слева, а затем найдем для него количество точек пересечения с горизонталью \(y=1\). Это и будет ответом на вопрос задачи (а).
Исследуем функцию: $$ f(x)=\frac1x+\frac<1>
1) ОДЗ: \(x\ne\left\<0;1;3\right\>\)
Все три точки – точки разрыва 2-го рода. \begin
Функция непериодическая.
3) Асимптоты
1. Вертикальные \(x=0, x=1, x=3\) – точки разрыва 2-го рода
2. Горизонтальные: \begin
На минус бесконечности функция стремится к 0 снизу, на плюс бесконечности – сверху.
3. Наклонные: \(k=0\), нет.
4) Первая производная $$ f'(x)=-\frac<1>
Функция убывает.
5) Вторую производную не исследуем, т.к. перегибы не влияют на количество точек пересечения с горизонталью.
6) Точки пересечения с OY – нет, т.к. \(x=0\) – асимптота
Точки пересечения с OX – две, \(0\lt x_1\lt 1,1\lt x_2\lt 3\)
7) График
Получаем ответ для задачи (а) 3 корня.
Решаем более общую задачу (б). Передвигаем горизонталь \(y=k\) снизу вверх и считаем количество точек пересечения с графиком функции. Последовательно, получаем:
При \(k\lt 0\) — три корня
При \(k=0\) — два корня
При \(k\gt 0\) — три корня
Ответ: а) 3 корня; б) при \(k=0\) два корня, при \(k\ne 0\) три корня.
Пример 3. Найдите все значения параметра a, при каждом из которых уравнение $$ \sqrt
Исследуем функцию \(f(x)=\sqrt
ОДЗ: \( \begin
Функция определена на конечном интервале.
Поэтому используем сокращенный алгоритм для построения графика.
Значения функции на концах интервала: \(f(1)=0+\sqrt<8>=2\sqrt<2>,\ f(5)=\sqrt<4>+0=2\)
Первая производная: \begin
| \(x\) | 1 | (1; 7/3) | 7/3 | (7/3; 5) | 5 |
| \(f'(x)\) | ∅ | + | 0 | — | ∅ |
| \(f(x)\) | \(2\sqrt<2>\) | \(\nearrow \) | max \(2\sqrt<3>\) | \(\searrow \) | 2 |
Можем строить график:
\(y=a\) — горизонтальная прямая.
Количество точек пересечения \(f(x)\) и \(y\) равно количеству решений.
Получаем:
| $$ a\lt 2 $$ | нет решений |
| $$ 2\leq a\lt 2\sqrt <2>$$ | 1 решение |
| $$ 2\sqrt<2>\leq a\lt 2\sqrt <3>$$ | 2 решения |
| $$ a=2\sqrt <3>$$ | 1 решение |
| $$ a\gt 2\sqrt <3>$$ | нет решений |
По крайней мере одно решение будет в интервале \(2\leq a\leq 2\sqrt<3>\).
п.3. Решение неравенств с построением графиков
Пример 4. Решите неравенство \(\frac<2+\log_3 x>
Разобьем неравенство на совокупность двух систем.
Если \(x\gt 1\), то \(x-1\gt 0\), на него можно умножить слева и справа и не менять знак.
Если \(x\lt 1\), то \(x-1\lt 0\), умножить также можно, только знак нужно поменять.
Сразу учтем требование ОДЗ для логарифма: \(x\gt 0\)
Получаем совокупность: \begin
Точка разрыва: \(x=\frac12\) – вертикальная асимптота
Односторонние пределы: \begin
Первая производная: $$ f'(x)=\left(1-\frac<3><2x-1>\right)’=\frac<3><(2x-1)^2>\gt 0 $$ Производная положительная на всей ОДЗ, функция возрастает.
Вторая производная: $$ f»(x)=-\frac<6> <(2x-1)^3>$$ Одна критическая точка 2-го порядка \(x=\frac12\)
Применение производной. Построение графиков с применением производных
Математика берет свои истоки со времен Античности. Благодаря ней архитектура, строительство и военное дело дали новый виток развития, достижения, которые были получены с помощью математики, привели к движению прогресса. И по сей день математика остается главной наукой, которая встречается во всех остальных отраслях.
Чтобы быть образованными, дети с первого класса начинают постепенно вливаться в эту среду. Очень важно разбираться в математике, так как она, в той или иной степени, встречается каждому человеку на протяжении всей его жизни. В этой статье будет разобран один из ключевых элементов — нахождение и применение производных. Не всякий человек может представить, насколько широко используется это понятие. Рассмотрим более 10 применений производных в определенных областях или науках.
Применение производной к исследованию функции
Производная — это такой предел отношения приращения функции к увеличению ее аргумента, когда показатель аргумента стремится к нулю. Производная — незаменимая вещь при исследовании функции. Например, с помощью нее можно определить возрастание и убывание последней, экстремумы, выпуклости и вогнутости. Дифференциальные исчисления входят в обязательную программу обучения студентов 1 и 2 курса математических вузов.
Область определения и нули функции
Первый этап любого исследования графика начинается с выяснения области определения, в более редких случаях — значения. Область определения задается по оси абсциссы, если говорить другими словами, то это числовые значения на оси OX. Часто область определения уже задана, но если она не задана, то следует оценить значение аргумента х. Допустим, если при каком-то значениях аргумента функция не имеет смысла, то этот аргумент исключается из области определения.
Нули функции находятся простым способом: функцию f(x) следует приравнивнять к нулю и решить полученное уравнение относительно одной переменной x. Полученные корни уравнения являются нулями функции, то есть в этих x функция равна 0.
Возрастание и убывание
Применение производной для исследования функций на монотонность может рассматриваться с двух позиций. Монотонная функция — это категория, которая имеет только положительные значения производной, либо только отрицательные. Простыми словами — функция только возрастает или только убывает на всем исследуемом промежутке:
- Параметр возрастания. Функция f(x) будет возрастать, если производная f`(x) больше нуля.
- Параметр убывания. Функция f(x) будет убывать, если производная f`(x) меньше нуля.
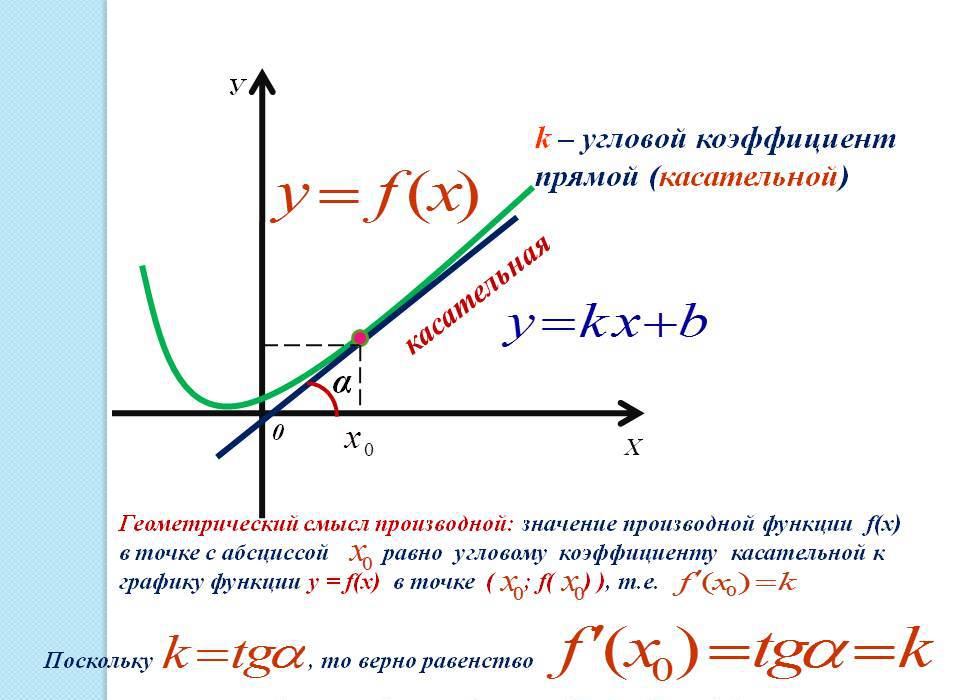
Касательная и угловой коэффициент
Применение производной к исследованию функции определяется еще и касательной (прямой, направленной под углом) к графику функции в данной точке. Касательная в точке (x0) — прямая, которая проходит через точку и принадлежит функции, координаты которой (x0, f(x0)), и имеющая угловой коэффициент f`(x0).
y = f(x0) + f`(x0)(x — x0) — уравнение касательной к данной точке графика функции.
Геометрический смысл производной: производная функции f(x) равняется угловому коэффициенту образованной касательной к графику этой функции в данной точке x. Угловой коэффициент, в свою очередь, равняется тангенсу угла наклона касательной к оси ОХ (абсцисс) в положительном направлении. Это следствие является основополагающим к применению производной к графику функции.
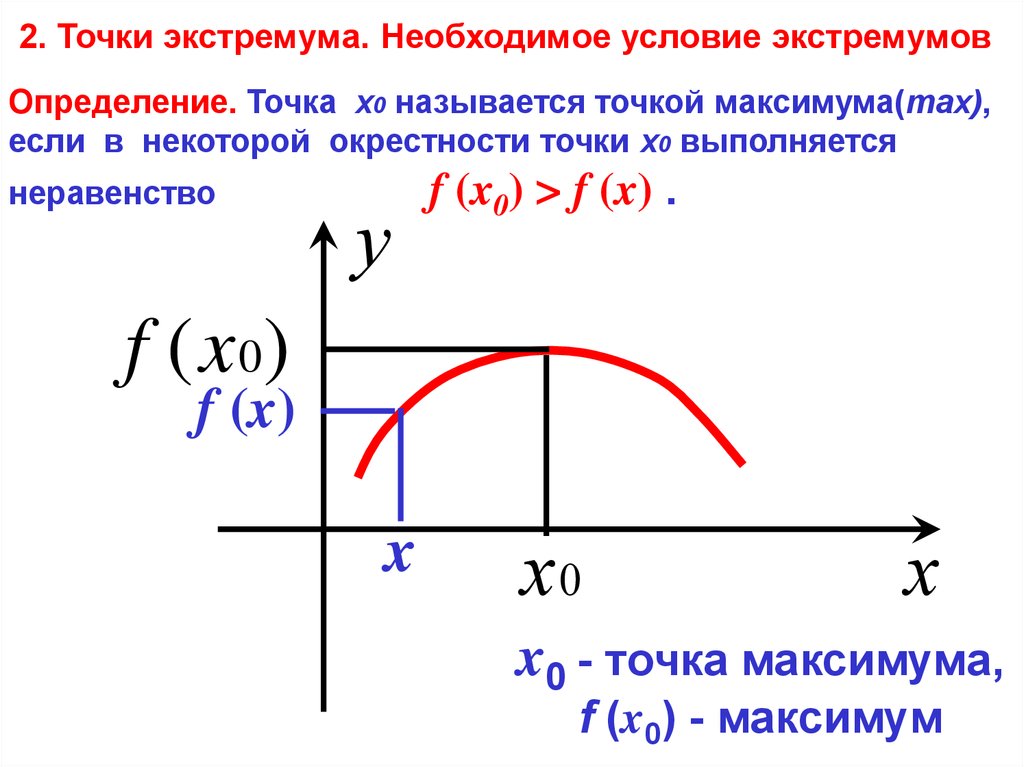
Точки экстремума
Применение производной к исследованию включает в себя нахождение точек максимума и минимума.
Для того чтобы найти и определить точки минимума и максимума, необходимо:
- Отыскать производную функции f(x).
- Приравнять полученное уравнение к нулю.
- Найти корни уравнения.
- Определить точки максимума и минимума.
Чтобы найти экстремумы функции:
- Отыскать точки минимума и максимума по способу выше.
- Подставить эти точки в первоначальное уравнение и высчитать yнаиб. и yнаим.
Точка максимума функции — это наибольшее значение функции f(x) на промежутке, другими словами xнаиб.
Точка минимума функции — это наименьшее значение функции f(x) на промежутке, другими словами xнаим.
Точки экстремума — то же самое, что и точки максимума и минимума, а экстремум функции (yнаиб. и унаим) — значения функций, которые соответствуют точкам экстремума.
Выпуклости и вогнутости
Определить выпуклость и вогнутость можно, прибегая к применению производной для построения графиков:
- Функция f(x), исследуемая на промежутке (a, b), является вогнутой, если функция расположена ниже всех своих касательных, находящихся внутри этого интервала.
- Функция f(x), исследуемая на промежутке (a, b), является выпуклой, если функция расположена выше всех своих касательных, находящихся внутри этого интервала.
Точка, которая разделяет выпуклость и вогнутость, называется точкой перегиба функции.
Чтобы найти точки перегиба:
- Найти критические точки второго рода (вторую производную).
- Точками перегиба являются те критические точки, которые разделяют два противоположенных знака.
- Вычисление значений функций в точках перегиба функции.
Частные производные
Применение производных такого типа есть в задачах, где используется больше одной неизвестной переменной. Чаще всего такие производные встречаются при построении графика функции, если быть точнее, то поверхности в пространстве, где вместо двух осей — три, следовательно, три величины (две переменные и одна постоянная).
Основное правило при вычислении частных производных — выбираем одну переменную, а остальные рассматриваем как постоянные. Следовательно, при вычислении частной производной постоянная величина становится как-будто числовым значением (во многих таблицах производных они обозначаются как C = const). Смысл такой производной — это скорость изменения функции z = f(x, y) по оси OX и OY, то есть характеризует крутизну впадин и выпуклостей построенной поверхности.
Производная в физике
Применение производной в физике имеет широкое распространение и значение. Физический смысл: производная пути по времени — скорость, а ускорение — производная скорости по времени. Из физического смысла можно провести множество ответвлений в различные разделы физики, при этом полностью сохраняя смысл производной.
С помощью применения производной находятся такие величины:
- Скорость в кинематике, где вычисляется производная от пройденного пути. Если находится вторая производная от пути или первая производная от скорости, то находится ускорение тела. Помимо этого, возможно нахождение мгновенной скорости материальной точки, однако для этого необходимо знать приращение ∆t и ∆r.
- В электродинамике: вычисление мгновенной силы переменного тока, а также ЭДС электромагнитной индукции. Вычисляя производную, можно найти максимальную мощность. Производная от количества электрического заряда — сила тока в проводнике.
Производная в химии и биологии
Химия: производная используется для определения скорости протекания химической реакции. Химический смысл производной: функция p = p(t), в данном случае p — количество вещества, которое вступает в химическую реакцию во времени t. ∆t — приращение времени, ∆p — приращение количества вещества. Предел отношения ∆p к ∆t, при котором ∆t стремится к нулю, называется скоростью протекания химической реакции. Среднее значение химической реакции — отношение ∆p/∆t. При определении скорости необходимо точно знать все необходимые параметры, условия, знать агрегатное состояние вещества и среду протекания. Это довольно большой аспект в химии, который широко применяется в различных отраслях и деятельности человека.
Биология: понятие производной используют при вычислении средней скорости размножения. Биологический смысл: имеем функцию y = x(t). ∆t — приращение по времени. Тогда с помощью некоторых преобразований получаем функцию y`= P(t) = x`(t) — активность жизнедеятельности популяции времени t (средняя скорость размножения). Такое применение производной позволяет вести статистику, отслеживать темпы размножения и так далее.
Производная в географии и экономике
Производная позволяет географам решать такие задачи, как нахождение численности населения, вычислять значения в сейсмографии, рассчитать радиоактивность ядерно-геофизических показателей, вычислить интерполяцию.
В экономике важную часть расчетов занимает дифференциальное исчисление и вычисление производной. В первую очередь это позволяет определить пределы необходимых экономических величин. Например, наибольшую и наименьшую производительность труда, издержки, прибыль. В основном эти величины рассчитываются по графикам функций, где находят экстремумы, определяют монотонность функции на нужном участке.
Заключение
Роль данного дифференциального исчисления задействована, как было отмечено в статье, в различных научных структурах. Применение производных функций — важный элемент в практической части науки и производства. Не зря нас в старшей школе и университете учили строить сложные графики, исследовать и работать над функциями. Как видим, без производных и дифференциальных исчислений невозможно было бы рассчитать жизненно важные показатели и величины. Человечество научилось моделировать различные процессы и исследовать их, решать сложные математические задачи. Действительно, математика — царица всех наук, потому что эта наука лежит в основе всех других естественных и технических дисциплин.
http://reshator.com/sprav/algebra/10-11-klass/primenenie-proizvodnoj-dlya-resheniya-nelinejnyh-uravnenij-i-neravenstv/
http://fb.ru/article/404955/primenenie-proizvodnoy-postroenie-grafikov-s-primeneniem-proizvodnyih
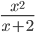 ≡ x^2/(x+2)
≡ x^2/(x+2) 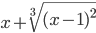 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)