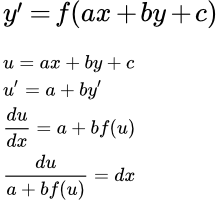Уравнения с разделяющимися переменными и приводимые к ним

Дифференциальные уравнения, приводящиеся к уравнениям с разделяющимися переменными

Постановка задачи

Рассмотрим дифференциальное уравнение
(i) ,
где f – функция, a, b, c – постоянные, b ≠ 0 .
Это уравнение приводится к уравнению с разделяющимися переменными.

Метод решения

Делаем подстановку:
u = ax + by + c
Здесь y – функция от переменной x . Поэтому u – тоже функция от переменной x .
Дифференцируем по x
u′ = ( ax + by + c )′ = a + by′
Подставляем (i)
u′ = a + by′ = a +b f ( ax + by + c ) = a + b f ( u )
Или:
(ii)
Разделяем переменные. Умножаем на dx и делим на a + b f ( u ) . Если a + b f ( u ) ≠ 0 , то

Интегрируя, мы получаем общий интеграл исходного уравнения (i) в квадратурах:
(iii) .

В заключении рассмотрим случай
(iv) a + b f ( u ) = 0 .
Предположим, что это уравнение имеет n корней u = r_i , a + b f ( r_i ) = 0 , i = 1, 2, . n . Поскольку функция u = r_i является постоянной, то ее производная по x равна нулю. Поэтому u = r_i является решением уравнения (ii).
Однако, уравнение (ii) не совпадает с исходным уравнением (i) и, возможно, не все решения u = r_i , выраженные через переменные x и y , удовлетворяют исходному уравнению (i).

Таким образом, решением исходного уравнения является общий интеграл (iii) и некоторые корни уравнения (iv).

Пример решения дифференциального уравнения, приводящегося к уравнению с разделяющимися переменными

Решить уравнение
(1)

Делаем подстановку:
u = x – y
Дифференцируем по x и выполняем преобразования:
;

Умножаем на dx и делим на u 2 .

Если u ≠ 0 , то получаем:

Интегрируем:

Применяем формулу из таблицы интегралов:

Вычисляем интеграл

Тогда
;
, или

Общее решение:
.

Теперь рассмотрим случай u = 0 , или u = x – y = 0 , или
y = x .
Поскольку y′ = ( x )′ = 1 , то y = x является решением исходного уравнения (1).

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 16-07-2012 Изменено: 22-02-2015

Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение вида называется уравнением с разделенными переменными .

Уравнение вида , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от и только от , называется уравнением с разделяющимися переменными .

Путем деления на произведение оно приводится к уравнению с разделенными переменными:

Общий интеграл этого уравнения имеет вид

Замечание. Деление на произведение может привести к потере частных решений, обращающих в ноль это произведение.

Дифференциальное уравнение вида

где и — постоянные, заменой переменных преобразуется в уравнение с разделяющимися переменными.

Пример 1. Решить уравнение .

Решение. Разделим обе части уравнения на произведение :

Получили уравнение с разделенными переменными. Интегрируя его, найдем

После потенцирования получим откуда

Обозначая , будем иметь или . Мы получили общий интеграл данного уравнения.

При делении на произведение предполагалось, что ни один из множителей не обращается в ноль. Приравняв каждый множитель нулю, получим соответственно .

Непосредственной подстановкой в исходное уравнение убеждаемся, что и являются решениями этого уравнения. Они могут быть формально получены из общего интеграла при и . Последнее означает, что постоянная заменяется через , после чего общий интеграл примет вид

Полагая в последнем равенстве , что соответствует , будем иметь, что , откуда и получаем решение исходного уравнения. Итак, функции и являются частными решениями данного уравнения. Поэтому окончательный ответ будет таким:

Пример 2. Найти частное решение уравнения , удовлетворяющее начальному условию .

Решение. Имеем Разделяя переменные, получаем . Интегрируя, найдем общий интеграл

Полагая и будем иметь , откуда .

Подставляя найденное значение , получаем частное решение

Из начального условия следует, что 0

(y|_=1>0)» png;base64,iVBORw0KGgoAAAANSUhEUgAAALcAAAAXBAMAAAC7XMNCAAAALVBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACttl6nAAAADnRSTlMAgUEYwJvlMGHQcVGxAUWyn3YAAALBSURBVEjHzZXPaxNBFMe/2c2aJelApRAEIWyl4KUsm2Baa6GUGi0eLIFoi0WLpgbFkrJFvIhKQRFyKWg9VEUp4smDFOzFS/AkeFu0ihW2JE1Da8D8Dc6PTfOjuxL1oA/C28x783kz33k7C/wjIxPC3/yTyaNegZjBnbIs/nb/GiMbrSMfbwMDhnu271KCR95a7cDlXGfLiJoZN8nXYff0+0bHaeZn0AacnBprhetacBok3Vju7m56BtImG7mItmTROTzQtTvwHnIFONOYk6tFA0UEytR3JH8Hjp5UbXGXQbYs6Ezal52IMk9yTjRUpEHqv9BJqykEzfbg6HGa69MWyKyFjRUg+GIbEX5+5J6g+4q8MoY0SBcqyK+4wGOHmB1ugqN3hDuJwscsvrYj37Zx0mqs7RMrJ7oG/+AOpgwX+Nx+Zgea4SQ+Ygk4KHyNqhpbz5JybU7vaMPKKVxVSuRxm5pTs+Mz9ZX7aS+Soc7Qzm5pBleLkLd4R1Hd38nl9uEk+pQ1BIVXBRyvTV/JCfZw0aQipLID15dp5UZ4cJK7qJssiC8xWaim5DuwxuARy58VdZ1mYn3O9kIPFAuaUmqCTwaTXgdKJRcPH0C3i3U2HDHuiIbOpYg42LChZJ1WzGt9zxrhcgGlVlnyydq+nb7ImypN2pinjwMnZufFS0ScbGVp3GSOTlIyz5MM/uqouMSkAjZb2GPV6o+mlwjKtTAl6oxhXZ9iba52OetmjfYGtde/f0GjcGUw/ZDLHC2g0rpy2+ZlU/X5x9hVco7+VbbljMeVlEaogkcWukkseLyL2JZt+wooejSNXZ/Iq1ylP//0wKJH+ip8V5RFfrcozqGpe2XxMJU1i5R44hX/vBxIPDAYvH+fpnFZ+l0O1H3bfWZ9E642IYJzCOtyUqSlQ8PW333m9tiNg2edr9at8yb+D/sJi9i08MuhxNYAAAAASUVORK5CYII=» style=»vertical-align: middle;» />, поэтому перед корнем берем знак плюс. Итак, искомое частное решение

Пример 3. Найти частные решения уравнения , удовлетворяющие начальным условиям: a) ; б) .

Решение. Имеем . Разделяем переменные . Интегрируя, найдем общий интеграл . После потенцирования получим или , что является общим решением исходного уравнения.

а) Положим , тогда , откуда . Искомое частное решение .

б) Полагая в общем решении , будем иметь откуда . Искомое частное решение .

Заметим, что в процессе получения общего решения постоянная входила под знак логарифма, и, значит, следует рассматривать как предельное значение. Это частное решение содержится среди нулей произведения , на которое мы делили обе части данного уравнения.

Пример 4. Найти такую кривую, проходящую через точку , чтобы тангенс угла наклона касательной в любой ее точке равнялся ординате этой точки, увеличенной на три единицы.

Решение. Исходя из геометрического свойства первой производной, получаем дифференциальное уравнение семейства кривых, удовлетворяющих требуемому в задаче свойству, а именно . Разделяя переменные и интегрируя, получаем общее решение

Так как искомая кривая должна проходить через точку , т.е. , то при получаем , откуда . Искомая кривая определится уравнением .

Пример 5. Найти кривую, обладающую тем свойством, что длина ее дуги, заключенной между какими-либо двумя точками и , пропорциональна разности расстояний этих точек от неподвижной точки .

Решение. Если фиксировать точку , то дуга будет изменяться пропорционально разности и постоянной . Введем полярные координаты, беря точку за полюс и — за полярную ось (рис. 11). Дифференциал дуги кривой в полярных координатах .

Отсюда для нашей задачи имеем или .

Интегрируя, находим (логарифмическая спираль).

Пример 6. Допустим, что при постоянной температуре скорость растворения твердого тела в жидкости пропорциональна количеству этого вещества, еще могущего раствориться в жидкости до насыщения последней (предполагается, что вещества, входящие в раствор, химически не действуют друг на друга, и раствор далек еще от насыщения, так как иначе линейный закон для скорости растворения неприменим). Найти зависимость количества растворившегося вещества от времени.

Решение. Пусть — количество вещества, дающее насыщенный раствор, и — количество уже растворившегося вещества. Тогда получаем дифференциальное уравнение , где — известный из опыта коэффициент пропорциональности, а — время.

Разделяя переменные, найдем .

Интегрируя, получаем откуда .

В начальный момент имеем , поэтому , так что окончательно .

Пример 7. В цилиндрическом сосуде объемом заключен атмосферный воздух, который адиабатически (без обмена тепла с окружающей средой) сжимается до объема . Вычислить работу сжатия.

Решение. Известно, что адиабатический процесс характеризуется уравнением Пуассона

где — первоначальный объем газа, — первоначальное давление газа, — постоянная для данного газа величина.

Обозначим через и соответственно объем и давление газа в тот момент, когда поршень находится на высоте , а через — площадь поршня. Тогда при опускании поршня на величину объем газа уменьшится на величину . При этом будет выполнена работа

Находя из (3) и подставляя в (4), получаем дифференциальное уравнение процесса

Интегрируя это уравнение, будем иметь

Согласно начальному условию получим .

Таким образом, работа адиабатического сжатия (от до ) будет .

Пример 8. Найти решение уравнения

Решение. Разделяя переменные и интегрируя, найдем общий интеграл уравнения: .

Начальное условие даёт , т. е. , так что частный интеграл будет иметь вид . Ему соответствует бесконечное множество частных решений вида

Среди этих решений имеется только одно, удовлетворяющее начальному условию. Это решение найдем, переходя к пределу при в равенстве (8):

Нетрудно видеть, что получившиеся уравнение имеет два корня: и , причем корень , отвечающий- знаку минус перед , не подходит, так как . Таким образом, искомое частное решение уравнения будет .

Дифференциальные уравнения с разделяющимися переменными и их интегрирование

п.1. Понятие дифференциального уравнения с разделяющимися переменными

Например:
\(y»+y’-4=5cos⁡x\) — ДУ второго порядка первой степени
\((y’)^3+5y^2=19\) – ДУ первого порядка третьей степени
\(\sqrt=y’x\) — ДУ первого порядка первой степени

Самыми простыми для решения будут такие уравнения, у которых можно разделить переменные, т.е. собрать всё, что связано с функцией \(y\), по одну сторону знака равенства, и всё, что связано с независимой переменной \(x\), — по другую сторону.

Например:
Уравнение \(\sqrt=y’x\) является уравнением с разделяющимися переменными, т.к. $$ y’=\frac<\sqrt>=g(x)\cdot h(y),\ \ \text<где>\ g(x)=\frac1x,\ h(y)=\sqrt $$

Алгоритм решения ДУ с разделяющимися переменными
На входе: уравнение первого порядка \(y’=f(x,y)\), для которого \(f(x,y)=g(x)\cdot h(y)\)
Шаг 1. Записать производную в форме Лейбница \(y’=\frac\)
Шаг 2. Преобразовать уравнение
$$ \frac=g(x)\cdot h(y)\Rightarrow \frac=g(x)dx $$ Шаг 3. Проинтегрировать левую и правую части уравнения: $$ \int\frac=\int g(x)dx+C $$ Шаг 4. Результат интегрирования \(H(y)=G(x)+C\) — общее решение данного уравнения.
На выходе: выражение \(H(y)=G(x)+C\)

Например:
Решим уравнение \(\sqrt=y’x\)
1) Пусть \(x\ne 0\). Тогда: $$ y’=\frac<\sqrt>\Rightarrow\frac=\frac<\sqrt>\Rightarrow\frac<\sqrt>=\frac $$ Находим интегралы (константу запишем в конце): $$ \int\frac<\sqrt>=\frac<(y+1)^<\frac32>><\frac32>=\frac23\sqrt<(y+1)^3>,\ \ \int\frac=\ln|x| $$ Получаем общее решение: $$ \frac23\sqrt<(y+1)^3>=\ln|x|+C,\ x\ne 0 $$ 2) Пусть \(x=0\). Тогда по условию: \(\sqrt=0\Rightarrow y=-1\)
Точка (0;-1) – особое решение данного уравнения.

п.2. Задача Коши

Например:
Найдем решение задачи Коши для уравнения \(\sqrt=y’x\) при начальном условии \(y(1)=3\).
Общее решение нами уже найдено: \(\frac23\sqrt<(y+1)^3>=\ln|x|+C\) — этим выражением задано бесконечное множество кривых. Решить задачу Коши означает найти единственную кривую, проходящую через точку (1;3), т.е. конкретное значение C для заданных начальных условий.
Подставляем \(x=1\) и \(y=3:\frac23\sqrt<(3+1)^3>=\underbrace<\ln 1>_<=0>+C\Rightarrow C=\frac23\sqrt<4^3>=\frac<16><3>\)
Решение задачи Коши: \(\frac23\sqrt<(y+1)^3>=\ln|x|+\frac<16><3>\)
Выразим y в явном виде, что всегда приходится делать на практике: $$ \sqrt<(y+1)^3>=\frac32\ln|x|+8\Rightarrow y+1=\left(\frac32\ln|x|+8\right)^<\frac23>\Rightarrow y=\left(\frac32\ln|x|+8\right)^<\frac23>-1 $$ Ограничения ОДЗ: \( \begin y\geq -1\\ \frac32\ln|x|+8\geq 0 \end \Rightarrow |x|\geq -\frac<16><3>\Rightarrow |x|\geq e^<-\frac<16><3>> \)
Начальная точка \(x=1\gt e^<-\frac<16><3>>\), требования ОДЗ выполняются.
Т.к. \(x=1\gt 0\) в решении также можно убрать модуль.

п.3. Закон радиоактивного распада

В многочисленных экспериментах по определению радиоактивности вещества был установлен следующий факт:

Число распадов ΔN, которые произошли за интервал времени Δt, пропорционально числу атомов N в образце.

Перейдем к бесконечно малым \(dN\) и \(dt\) и запишем соответствующее этому факту дифференциальное уравнение: $$ \frac

=-\lambda N $$ где знак «-» учитывает уменьшение числа атомов N со временем.
Полученное ДУ является уравнением с разделяющимися переменными.
Найдем его общее решение: $$ \frac=-\lambda dt\Rightarrow\int\frac=-\lambda\int dt\Rightarrow \ln N=-\lambda t+C $$ Пусть в начальный момент времени \(t=0\) в образце было \(N_0\) атомов.
Решаем задачу Коши, находим \(C:\ \ln N_0=-\lambda\cdot 0+C\Rightarrow C=\ln N_0\)
Подставляем найденное C в общее решение. Получаем: $$ \ln N=-\lambda N+\ln N_0\Rightarrow \ln N-\ln N_0=-\lambda t\Rightarrow\ln\frac=-\lambda t\Rightarrow\frac=e^ <-\lambda t>$$

п.4. Зарядка конденсатора

Соберем цепь, состоящую из конденсатора C, резистора R, источника ЭДС E и ключа K. Пусть в начальный момент времени конденсатор разряжен, напряжение на обкладках: \(U(0)=0\) Замкнем ключ и начнем зарядку конденсатора.

По закону Ома для замкнутой цепи можем записать: $$ I(R+r_0)+U=\varepsilon $$ где \(I\) — ток в цепи, \(I(R+r_0)\) – падение напряжения на резисторе и источнике, \(U\) — напряжение на конденсаторе, \(\varepsilon\) – ЭДС источника.
Ток в цепи равен производной от заряда по времени: $$ I=\frac

=\frac

=C\frac

$$ Подставляем: $$ C\frac

\cdot (R+r_0)=\varepsilon-U $$ Получили ДУ с разделяющимися переменными: $$ \frac<\varepsilon-U>=\frac

$$ Интегрируем (не забываем про минус перед U в знаменателе): $$ \int\frac<\varepsilon-U>=-\ln(\varepsilon-U),\ \ \int\frac = \frac $$ Общее решение: $$ \ln(\varepsilon-U)=-\frac+B $$ где \(B\) константа, которую мы обозначили так, чтобы не путать с емкостью.
Начальное условие \(U(0)=0\). Подставляем: $$ \ln(\varepsilon-0)=-\frac<0>+B\Rightarrow B=\ln\varepsilon $$ Решение задачи Коши: \begin \ln(\varepsilon-U)=-\frac+\ln\varepsilon\\ \ln(\varepsilon-U)-\ln\varepsilon=-\frac\\ \ln\frac<\varepsilon-U><\varepsilon>=-\frac\Rightarrow\frac<\varepsilon-U><\varepsilon>=e^<-\frac>\Rightarrow \varepsilon e^<-\frac> \end

Если внутренне сопротивление источника пренебрежимо мало по сравнению с внешним сопротивлением, \(r_0\lt\lt R\), то получаем: $$ u(t)=\varepsilon\left(1-e^<-\frac>\right) $$ При \(t\rightarrow +\infty\) показатель экспоненты стремится к (\(-\infty\)), а сама экспонента стремится к нулю: \(U(t\rightarrow +\infty)=\varepsilon(1-e^<-\infty>)\), т.е. напряжение на обкладках конденсатора стремится к значению ЭДС источника.

Например:
При \(\varepsilon=5В,\ RC=0,01\) с график зарядки конденсатора имеет вид:

п.5. Примеры

Пример 1. Решите уравнение:
a) \(y’=e^\) \begin \frac=e^x\cdot e^y\Rightarrow e^<-y>dy=e^x dx\Rightarrow\int e^<-y>dy=\int e^x dx\Rightarrow -e^<-y>=e^x+C \end \(e^<-y>=-e^x+C\) (на константу, определенную от минус до плюс бесконечности, перемена знака не влияет).
\(-y=\ln⁡(-e^x+C) \)
\(y=-\ln⁡(C-e^x)\)
Ответ: \(y=\ln⁡(C-e^x)\)

б) \(xy+(x+1)y’=0\) \begin (x+1)y’=-xy\Rightarrow\frac=-\frac\Rightarrow\frac=-\fracdx\\ \int\frac=\ln|y|\\ -\int\fracdx=-\int\frac<(x+1)-1>dx=-\int\left(1-\frac<1>\right)dx=-x+\ln|x+1| \end Получаем: \(\ln|y|=-x+\ln|x+1|\)
Запишем константу немного по-другому, как \(\ln ⁡C\). Это удобно для потенцирования: \begin \ln|y|-x+\ln|x+1|+\ln C\\ \ln|y|-\ln C=-x+\ln|x+1|\\ \ln\frac<|y|>=-x+\ln|x+1|\\ e^<\ln\frac<|y|>>=e^<-x+\ln|x+1|>\\ \frac yC=e^<-x>\cdot (x+1)\\ y=Ce^<-x>(x+1) \end При преобразованиях мы делили на \((x+1)\) и \(y\), считая, что \(x\ne -1\) и \(y\ne 0\). Если подставить \(x=-1\) в решение, получим \(y=0\), т.е. эта точка не является особой, она входит в общее решение.
Ответ: \(y=Ce^<-x>(x+1)\)

Пример 2*. Найдите решение задачи Коши:
a) \(\frac+e^y=0,\ y(1)=0\) \begin \frac=-e^y\Rightarrow\frac=-x^2e^y\Rightarrow e^<-y>dy=-x^2dx\\ \int e^<-y>dy=-e^<-y>,\ \ -\int x^2dx=-\frac <3>\end Получаем: \begin -e^<-y>=-\frac<3>+C\Rightarrow e^<-y>=\frac<3>+C\Rightarrow -y=\ln\left|\frac<3>+C\right|\Rightarrow y=-\ln\left|\frac<3>+C\right| \end Общее решение: \(y=-\ln\left|\frac<3>+C\right|\)
Решаем задачу Коши. Подставляем начальные условия: $$ 0-\ln\left|\frac13+C\right|\Rightarrow\frac13+C=1\Rightarrow C=\frac23 $$ Решение задачи Коши: \(y=-\ln\left|\frac<3>\right|\)
Ответ: \(y=-\ln\left|\frac<3>\right|\)

б) \(x^2(y^2+5)+y^2(x^2+r)y’=0,\ y(0)=\sqrt<5>\) \begin y^2(x^2+5)y’=-x^2(y^2+5)\\ y’=\frac=-\frac\Rightarrow \fracdy=-\fracdx \end Используем табличный интеграл: \(\int\frac=\frac1a arctg\frac xa+C\) \begin \int\fracdy=\int\frac<(y^2+5)-5>dy=\int\left(1-\frac<5>\right)dy=y-5\cdot\frac<1><\sqrt<5>>arctg\frac<\sqrt<5>>=\\ =y-\sqrt<5>arctg\frac<\sqrt<5>> \end Аналогично: \(-\int\fracdx=-x+\sqrt<5>arctg\frac<\sqrt<5>>\)
Общее решение: \(y-\sqrt<5>arctg\frac<\sqrt<5>>=-x+\sqrt<5>arctg\frac<\sqrt<5>>+C\)
Решаем задачу Коши. Подставляем начальные условия: $$ \sqrt<5>-\sqrt<5>arctg1=-0+0+C\Rightarrow C=\sqrt<5>-\frac<\pi\sqrt<5>><4>=\sqrt<5>\left(1-\frac\pi 4\right) $$ Решение задачи Коши: \(y-\sqrt<5>arctg\frac<\sqrt<5>>=-x+\sqrt<5>arctg\frac<\sqrt<5>>+\sqrt<5>\left(1-\frac\pi 4\right)\)
Ответ: \(y-\sqrt<5>arctg\frac<\sqrt<5>>=-x+\sqrt<5>arctg\frac<\sqrt<5>>+\sqrt<5>\left(1-\frac\pi 4\right)\)

Пример 3. Найдите массу радиоактивного вещества спустя время, равное четырем периодам полураспада, если начальная масса составляла 64 г.
При радиоактивном распаде атомы одного элемента превращаются в атомы другого, поэтому для массы вещества справедлив тот же закон, что и для количества атомов этого вещества: $$ m(t)=m_0 e^ <-\lambda t>$$ Период полураспада – это время, за которое масса уменьшается в 2 раза: $$ \frac\right)>=\frac12 $$ За время, равное 4 периодам полураспада, масса уменьшится: $$ \frac\right)>=\left(\frac12\right)^4=\frac<1> <16>$$ в 16 раз.
Получаем: $$ m\left(4T_<\frac12>\right)=\frac<16>,\ \ m\left(4T_<\frac12>\right)=\frac<64><16>=4\ \text <(г)>$$ Ответ: 4 г

Пример 4. Выведите зависимость \(U(t)\) на обкладках конденсатора при его разрядке в RC-цепи.

Разрядка конденсатора происходит в цепи без источника ЭДС. Пусть в начальный момент заряд на обкладках \(U(0)=U_0.\) Замкнем ключ и начнем разрядку конденсатора.

По закону Ома для замкнутой цепи: $$ IR+U=0 $$ Ток в цепи равен производной от заряда по времени: $$ I=\frac

=\frac

=C\frac

$$ Подставляем: $$ RC\frac

=-U $$ Получили ДУ с разделяющимися переменными: $$ \frac=-\frac

$$ Интегрируем: $$ \int\frac=\ln U,\ \ \int

=\frac $$ Общее решение: $$ \ln U=-\frac+B $$ где \(B\) константа, которую мы обозначили так, чтобы не путать с емкостью.
Начальное условие \(U(0)=0\). Подставляем: $$ \ln U_0=-\frac<0>+B\Rightarrow B=\ln U_0 $$ Решение задачи Коши: \begin \ln U=-\frac+\ln U_0\Rightarrow\ln U-\ln U_0=-\frac\Rightarrow \ln\frac=-\frac\\ \frac=e^<-\frac> \end

Изменение напряжение на обкладках конденсатора при разрядке: $$ U(t)=U_0 e^<-\frac> $$

Например, \(при U_0=5В,\ RC=0,01 с\) график разрядки конденсатора имеет вид:

источники:

http://mathhelpplanet.com/static.php?p=differentsialnye-uravneniya-s-razdelyayushchimisya-peremennymi

http://reshator.com/sprav/algebra/10-11-klass/differencialnye-uravneniya-s-razdelyayushchimisya-peremennymi-i-ih-integrirovanie/