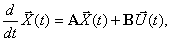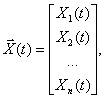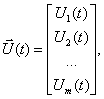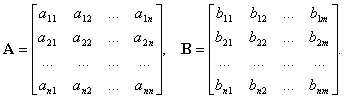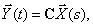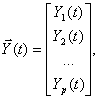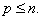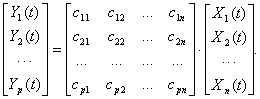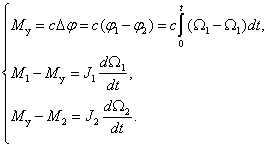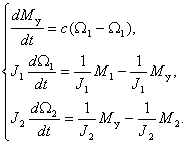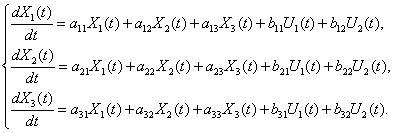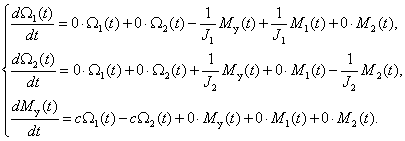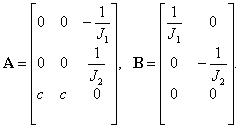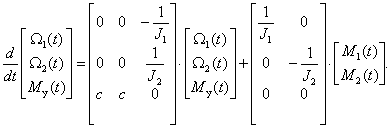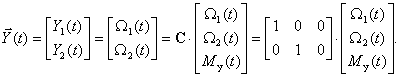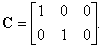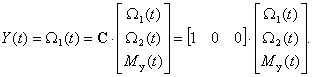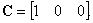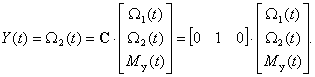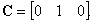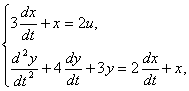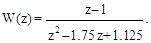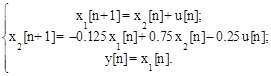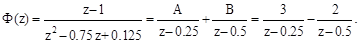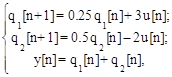Уравнения с в пространстве состояний

Уравнения с в пространстве состояний

Математические модели в пространстве состояний

Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид –

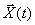
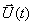
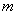
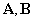
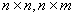
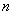
где — вектор состояния размерности , который включает в себя переменные объекта, однозначно определяющие его состояние,

— вектор управления или входа размерности , который включает в себя сигналы, действующие на систему извне,

— матрицы параметров, включающие в себя параметры системы, размерность которых соответственно ,

— порядок системы.

Иногда уравнение состояния (1) записывают в развернутой форме –

.

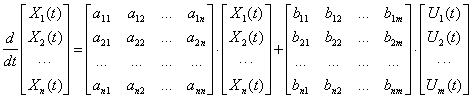
Уравнение состояния и структура полностью описывают объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.

Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы) –

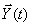
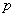
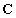
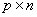
где — вектор выхода размерности , который содержит переменные объекта, доступные для наблюдения,

— матрица параметров размерности –

в системах управления

Уравнение выхода (2) также можно записать в развернутой форме

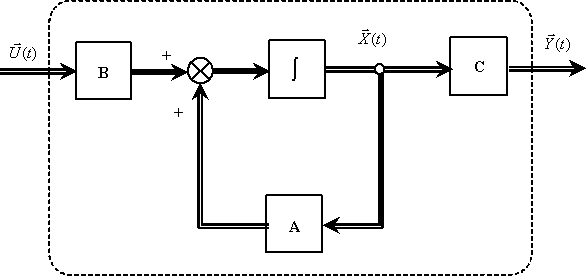
Графически уравнение состояния и уравнение выхода могут быть представлены в виде, показанном на рис. 1.

Символ интегрирования на схеме означает покомпонентное интегрирование векторной величины.

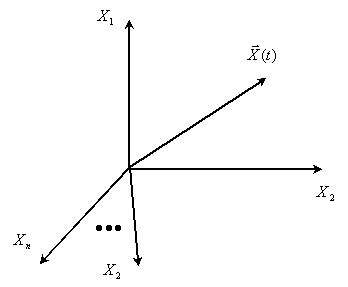
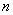
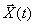
В общем виде пространство состояний — мерной системы задается радиус-вектором в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.

Рассмотрим несколько примеров представления процессов в пространстве состояний.

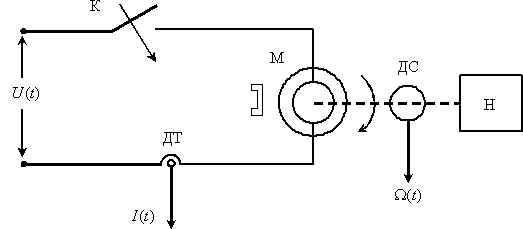
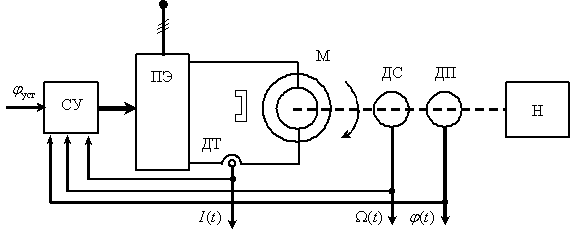
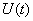
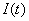
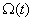
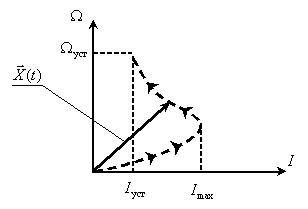
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 3. Пуск производится подключением с помощью контакта (К) напряжения , при этом в цепи будет протекать ток и двигатель будет вращать вал с нагрузкой (Н) со скоростью , ток и скорость определяются с помощью датчиков соответственно ДТ ДС.

Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задаем в следующем виде –

.

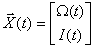
Вектор входа будет иметь только одну компоненту 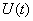. Графики изменения во времени переменных двигателя показаны на рис. 4.

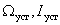
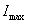
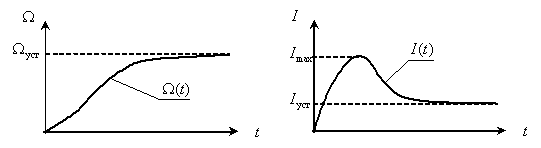
На рис. 4 введены обозначения: — установившиеся значения соответственно скорости и тока, – максимальное значение тока при пуске.

Сформируем двухмерное пространство состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.

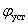
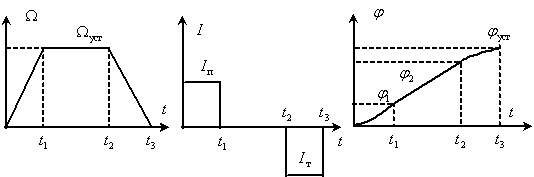
Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение , в автоматизированном электроприводе, показанном на рис. 6.

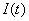
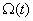
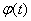
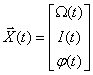
В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменные двигателя ток , скорость и положение вала –

.

Графики изменения во времени переменных двигателя показаны на рис. 7.

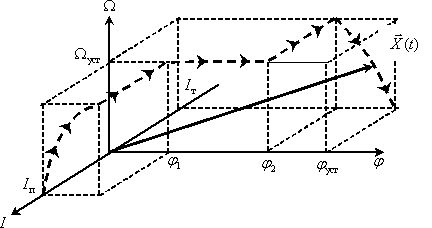
Сформируем трехмерное пространство состояний электропривода с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам изменения компонент вектора состояния.

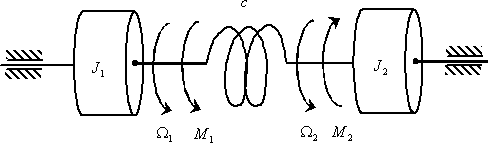
Теперь рассмотрим получения математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 9.

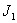
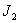
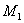
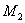
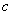
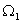
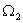
Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции и . К каждой массе прикладывается извне момент ( и ), массы соединены валом, обладающим упругими свойствами (), массы вращаются со скоростями и .

Система дифференциальных уравнений, описывающих систему, имеет вид –

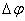
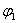
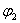
где – разность углов положения первой и второй масс.

Так как уравнения состояния (1) и выхода (2) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы мы должны выполнить следующее:

задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,

определить матрицы параметров уравнений.

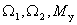
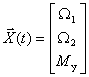
Состояние системы определяется тремя переменными , поэтому задаем вектор состояния следующего вида –

.

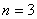
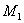
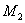
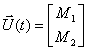
Порядок системы . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты и , поэтому вектор входа имеет вид –

.

Порядок вектора выхода 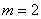. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.

Преобразуем уравнения системы (3) к форме Коши –

Нам требуется получить уравнение состояния для системы третьего порядка с вектором входа второго порядка, посмотрим, что представляет собой это уравнение в общем виде –

.

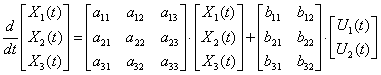
Раскрывая матричные скобки, получим –

Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (4) в виду (5), для этого следует:

расположить уравнения в порядке следования компонент в векторе состояния,

расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,

отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.

В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.

Преобразуем систему (4) к виду (5), в результате получим –

В результате по коэффициентам слагаемых в правых частях (6) получим искомые матрицы параметров уравнения состояния –

Уравнение состояния в развернутом виде –

Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианты датчиковых систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):

Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода –

То есть имеем ,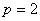

Датчик скорости установлен на первой массе, уравнение выхода –

,

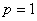
Датчик скорости установлен на второй массе, уравнение выхода –

,

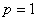
Контрольные вопросы и задачи

Перечислите компоненты уравнения состояния (векторы и матрицы), их размерности.

Поясните смысл уравнения выхода, перечислите компоненты и их размерности.

По системе дифференциальных уравнений, описывающих многомерную систему –

,

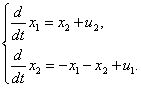
полагая векторы состояния и входа –

,

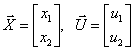
записать уравнение состояния в развернутой форме.

.

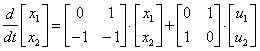
По уравнению состояния

,

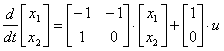
описывающему многомерную систему, определить систему дифференциальных уравнений, связывающих компоненты векторов состояния и входа.

..

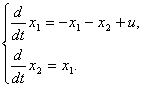
По системе дифференциальных уравнений, описывающих многомерную систему –

полагая векторы состояния и входа –

,

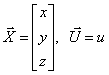
записать уравнение состояния в развернутой форме.

.

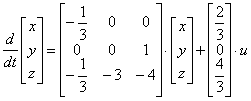
Пространство состояний в задачах проектирования систем оптимального управления

Введение

Исследование системы управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа.

Состоянию системы соответствует точка в определённом евклидовом пространстве, а поведение системы во времени характеризуется траекторией, описываемой этой точкой.

При этом математический аппарат включает готовые решения по аналоговому и дискретному LQR и DLQR контролерам, фильтра Калмана, и всё это с применением матриц и векторов, что и позволяет записывать уравнения системы управления в обобщённом виде, получая дополнительную информацию при их решении.

Целью данной публикации является рассмотрение решения задач проектирования систем оптимального управления методом описания пространства состояний с использованием программных средств Python.

Теория кратко

Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:

(1)

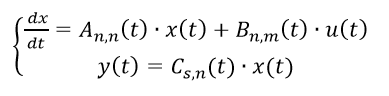
Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным объектом. В противном случае объект будет нестационарным.

При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:

(2)

где y(t) – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).

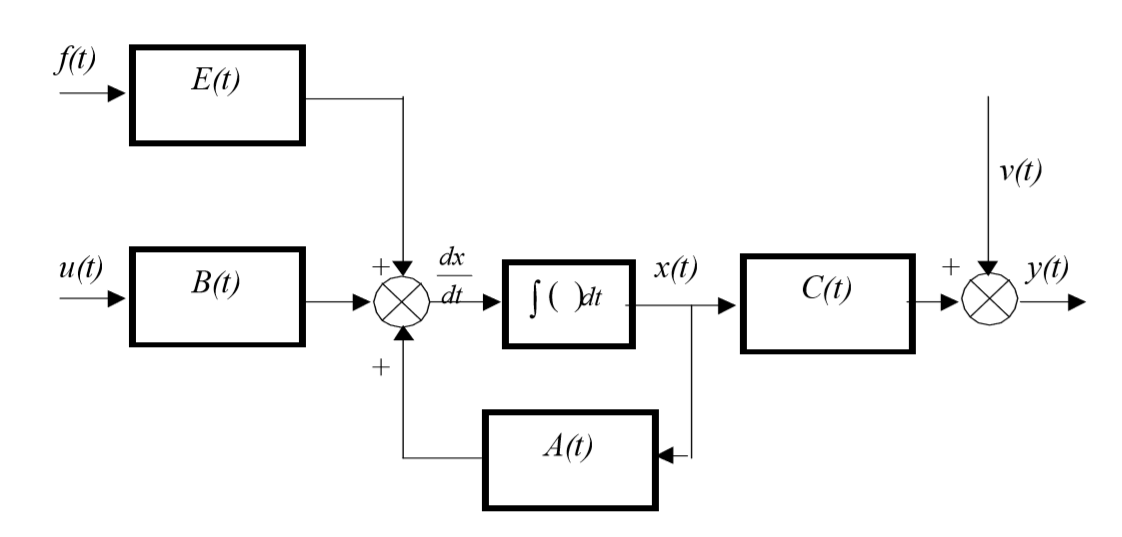
Структура линейной непрерывной системы, реализующая уравнения (1) и (2), приведена на рисунке:

Данная структура соответствует математической модели объекта, построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).

Для примера рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов. Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть так:

(3)

Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе — условия механического равновесия. В качестве обобщенных координат выберем ток якоря I и частоту вращения якоря ω.

Управлением являются напряжение на якоре U, возмущением — момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см (в системе СИ: Cе=См).

Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.

(4)

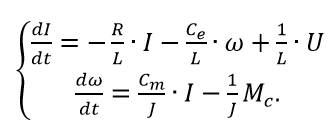
В матричном виде уравнения (4) примут вид (1):

(5)

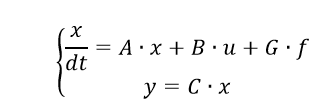
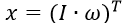
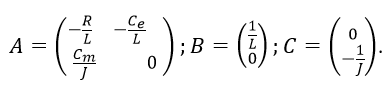
где вектор обобщенных координат , вектор управлений U =u (в рассматриваемом случае он является скаляром), вектор (скаляр) возмущений Mc=f. Матрицы модели:

(6)

Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде:

(7)

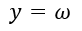
а матрица измерений примет вид:

Сформируем модель двигателя в Python. Для этого вначале зададим конкретные значения параметров двигателя: U = 110 В; R =0,2 Ом; L = 0,006 Гн; J =0,1 кг/м2;Ce =Cm=1,3 В/С и найдем значения коэффициентом матриц объекта из (6).

Разработка программы формирующей модель двигателя с проверкой матриц на наблюдаемость и управляемость:

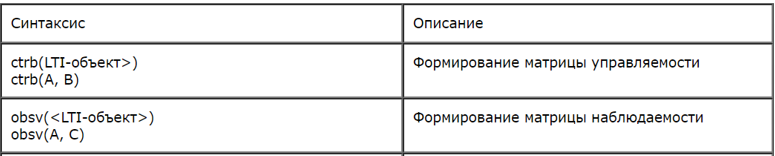
При разработке программы использовалась специальная функция def matrix_rank для определения ранга матрицы и функции, приведенные в таблице:

Результаты работы программы:

Матрица А:
[[ -33.33333333 -216.66666667]
[ 13. 0. ]]
Матрица B:
[[166.66666667]
[ 0. ]]
Матрица C:
[[0 1]]
Скаляр D:
0
Передаточная функция двигателя:
2167/(s^2 + 33.33 s + 2817)
Ранг матрицы управляемости: 2
Ранг матрицы наблюдаемости: 2

1. На примере двигателя постоянного тока с независимым магнитным возбуждением рассмотрена методика проектирования управления в пространстве состояний;

2. В результате работы программы получены передаточная функция, переходная характеристика, а так же ранги матриц управляемости и наблюдаемости. Ранги совпадают с размерностями пространства состояний, что подтверждает управляемость и наблюдаемость модели.

Пример проектирования оптимальной системы управления с дискретным dlqr контролером и полной обратной связью

Определения и терминология

Линейно-квадратичный регулятор (англ. Linear quadratic regulator, LQR) — в теории управления один из видов оптимальных регуляторов, использующий квадратичный функционал качества.

Задача, в которой система описывается линейными дифференциальными уравнениями, а показатель качества, представляет собой квадратичный функционал, называется задачей линейно-квадратичного управления.

Широкое распространение получили линейно-квадратичные регуляторы (LQR) и линейно-квадратичные гауссовы регуляторы (LQG).

Приступая к практическому решению задачи всегда нужно помнить об ограничениях

Для синтеза оптимального дискретного регулятора линейных стационарных систем нужна функция численного решения уравнения Беллмана.Такой функции в библиотеке Python Control Systems [1] нет, но можно воспользоваться функцией для решения уравнения Риккати, приведенной в публикации [2]:

Но нужно ещё учесть ограничения на синтез оптимального регулятора, приведенные в [3]:

• система, определяемая матрицами (A, B) должна быть стабилизируема;
• должны выполняться неравенства S> 0, Q – N/R–N.T>0, пара матриц (Q – N/R–N.T,
  A – B/R–B.T) не должна иметь наблюдаемые моды с собственными значениями на
  действительной оси.

После копаний в обширной и не однозначной теории, которую, по понятным причинам, я не привожу, задачу удалось решить, и все ответы можно прочитать прямо в комментариях к коду.

Структурная схема регулятора системы управления с обратной связью по всем переменным состояния изображена на рисунке:

Для каждого начального состояния x0 оптимальный линейный регулятор порождает оптимальное программное управление u*(x, k) и оптимальную траекторию х*(k).

Программа, формирующая модель оптимального управления с dlqr контролером

K=
[[ 0.82287566 -0.17712434]
[ 0.82287566 -0.17712434]]
P=
[[ 3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E=
[0.17712434+0.17712434j 0.17712434-0.17712434j]

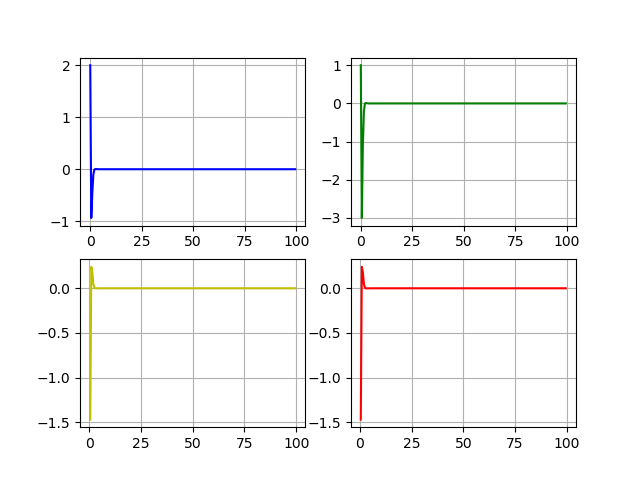
Динамика состояний и управлений: x1, x2, u1, u2.

Вывод

Отдельные задачи оптимального управления по типу приведенных можно решать средствами Python, комбинируя возможности библиотек Python Control Systems, SciPy,NumPy, что, безусловно, способствует популяризации Python, учитывая, что ранее такие задачи можно было решать только в платных математических пакетах.

Описание дискретных систем в пространстве состояний

Современная теория дискретных систем, так же как и непрерывных, базируется на описании их в пространстве состояний [9].

Рассмотрим дискретную систему m-го порядка с одним входом u[n] и одним выходом y[n], передаточная функция которой в общем виде может быть записана следующим образом

(1.122)

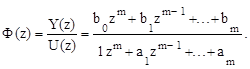
Если порядок числителя передаточной функции окажется меньше порядка знаменателя, т.е. l -1 — блок запаздывания; A,B,C,D — блоки матричных усилителей

Переменные состояния — это дискретные значения сигнала в текущий момент времени и m-1 его значений в предыдущие моменты времени.

Аналогично непрерывным системам составляющие вектора переменных состояний x_i[n] рассматривают как оси координат многомерного пространства состояния системы. С течением времени вектор состояния изменяет свое значение и положение, его конец описывает в пространстве состояния некоторую кривую, называемую траекторией движения системы.

Матрица системы A определяет устойчивость и другие показатели качества работы системы, матрица управления B характеризует влияние на переменные состояния входного воздействия, а матрица наблюдения C устанавливает связь выходной величины системы с вектором переменных состояния. Выбор переменных состояния в дискретных системах, как и в непрерывных, является неоднозначной операцией, т.е. векторное разностное уравнение зависит от выбранных переменных состояния. Однако все возможные векторные уравнения эквивалентны, так как описывают один и тот же динамический процесс связи выходной переменной системы с входным воздействием.

В общем случае дискретная система имеет k входов и r выходов. При этом вид векторных уравнений остается таким же (1.126), в которых матрица системы A имеет тот же вид, что и в системах с одним входом и одним выходом, матрица управления становится прямоугольной размером m´k, а матрица наблюдения имеет размер r´m.

Дискретная матрица переходов устанавливает связь между значениями вектора переменных состояния в различные отсчеты времени и для стационарных систем определяется как [9]

Матрицу [zE — A] называют характеристической, определитель этой матрицы образует характеристическое уравнение системы.

Таким образом, решение векторного разностного уравнения имеет вид

(1.128)

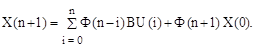
Пример. Найти описание в пространстве состояний системы, дискретная передаточная функция разомкнутой цепи которой имеет вид

Р е ш е н и е . Определяем дискретную передаточную функцию замкнутой системы

,

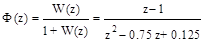
которой соответствует разностное уравнение

y[n+2] — 0.75 y[n+1] + 0.125y[n] = u[n+1] — u[n].

На основании выражений (1.125) и (1.126) получаем

С = [1 0]; D = [0].

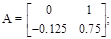
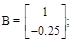
Уравнения системы в пространстве состояний

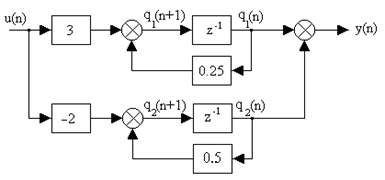
По полученным уравнениям на рис. 1.24,а изображена структурная схема системы, в которой переменные состояния — это выходные величины звеньев задержки.

Найдем полюса (z₁ = 0.5; z₂ = 0.25) дискретной передаточной функции системы и разложим ее на простейшие дроби

Структурная схема системы представлена на рис. 1.24,б.

а)

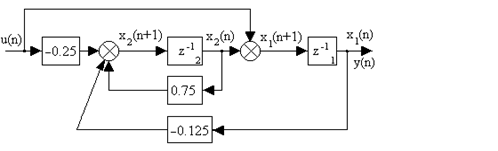
Рис. 1.24. Структурная схема дискретной системы второго порядка:

а — относительно выходов; б — относительно полюсов системы

Выбрав в качестве переменных состояния выходные величины звеньев задержки, получим следующую систему уравнений:

С_n = [1 1]; D_n = [0].

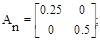
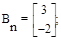
В отличие от рассмотренного ранее описания переменные в разностных уравнениях развязаны между собой. Такая запись называется нормальной формой описания дискретной системы в пространстве состояний.

ВОПРОСЫ К РАЗДЕЛУ 1

1. Сформулируйте определение дискретных систем. Какова структура и классификация импульсных систем?

2. Расскажите о математическом аппарате исследования импульсных систем.

3. Сформулируйте теорему Котельникова-Шеннона. Поясните ее физический смысл и практическое значение при проектировании дискретных систем.

4. Поясните методы определения передаточных функций импульсных систем. Каковы особенности передаточных функций статических и астатических систем?

5. Каким образом определяются частотные характеристики импульсных систем?

6. Какими способами определяются переходные процессы в дискретных системах?

7. Сформулируйте условия устойчивости импульсных систем.

8. Каким образом оценивается точность работы импульсных систем?

9. Каков порядок синтеза цифровых систем? Перечислите методы определения передаточных функций корректирующих устройств. Укажите виды структурных схем цифровых фильтров.

10.Запишите стандартную форму уравнений в пространстве состояний. Поясните физический смысл уравнений.