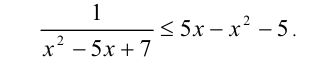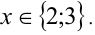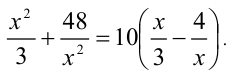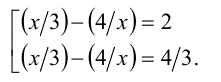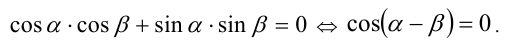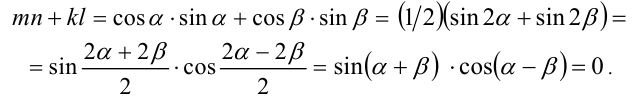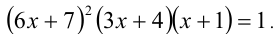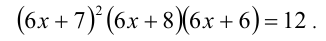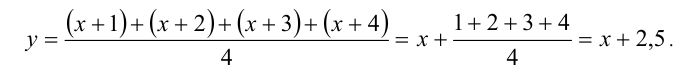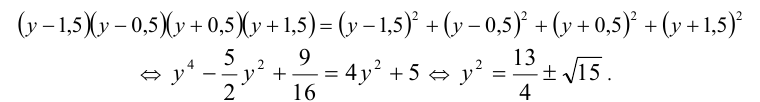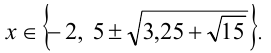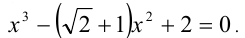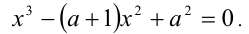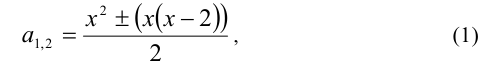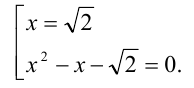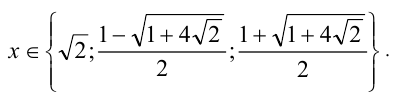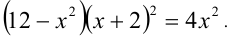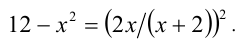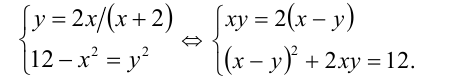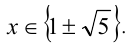Уравнения с заменой на t

Метод замены переменной

Метод замены переменной – это такой способ решения, при котором в уравнение (или неравенство) вводится новая переменная, в результате чего оно становится более простым.

Этот метод один из самых популярных при решении сложных заданий, в частности, в ЕГЭ и ОГЭ.

У нас довольно сложное уравнение. А если раскрыть скобки, оно станет еще сложнее. Что делать? Давайте попробуем заменить переменную.

Заменим выражение \(x+\frac<1>\) буквой \(t\).

Получилось обычное квадратное уравнение! Решив его, найдем чему равно \(t\), после чего, сделав обратную замену, вычислим \(x\).

Когда не стоит вводить новую переменную? Когда это не сделает уравнение проще. Например, если старая переменная остается, несмотря на замену:

Попробуем сделать замену здесь.

Заменим выражение \(\sin x\) буквой \(t\).

Видим, что в этой замене нет никакого смысла – она не упростила уравнение, даже наоборот, усложнила его, потому что теперь у нас в уравнении две переменные.

Примеры использования метода замены переменной

Заметим, что \(x^4=(x^2 )^2\) (см. свойства степеней ). Тогда наше уравнение приобретает следующий вид.

Теперь используем метод замены.

Вводим новую переменную, заменяя \(x^2\) на \(t\).

Мы нашли чему равно \(t\), но найти-то надо иксы! Поэтому делаем обратную замену.

Ответ: \(±1\); \(±\) \(\frac<1><2>\) .

Весьма частая ошибка при использовании этого метода: забыть «вернуться к иксам», то есть не сделать обратную замену. Помните – нам нужно найти \(x\), а не \(t\)! Поэтому возврат к \(x\) — строго обязателен!

Пример. Решить неравенство: \(\log^2_3⁡x-\log_3⁡x-2>0\)

Приступим к решению.

Раскладываем левую часть неравенства на множители .

Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности , имеющей такое же решение, и сделаем обратную замену.

Метод замены переменных при решении уравнений и неравенств

Метод замены переменных

Этот распространённый метод используется для разных целей: упрощение задачи и повышение её наглядности, придание уравнению (неравенству, системе и проч.) более симметричного вида, сведение одного уравнения к системе нескольких уравнений, рационализация иррациональностей (см. пункт 3.3) и т.д. Иными словами, введение новых переменных производится в тех случаях, когда есть возможность свести задачу к другой, для которой существует более эффективный способ решения.

Существуют виды уравнений, для которых разработаны специальные подстановки, позволяющие наиболее оптимально решать эти уравнения (например, симметрические и возвратные уравнения, однородные уравнения и многие другие). Рассмотрим дополнительно группу примеров, иллюстрирующих различные цели использования этого подхода.

Начнём с примера, в котором при помощи замены неизвестной рациональное неравенство сводится также к рациональному, но более простому алгебраическому неравенству.

Пример №350.

Решение:

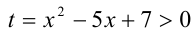
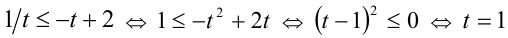
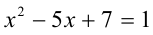
Положим . Тогда необходимо решить неравенство . Выполнив обратную подстановку, получим квадратное уравнение , решив которое, приходим к ответу. Ответ:

В следующем примере дробно-рациональное уравнение заменой сводится к целому алгебраическому уравнению.

Пример №351.

Решить уравнение

Решение:

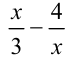
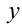
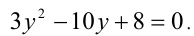
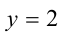
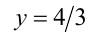
Обозначим разность через , тогда уравнение перепишется в виде Это уравнение имеет два корня и , что приводит к совокупности уравнений

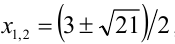
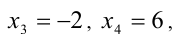
Первое уравнение даёт корни , а второе — которые и будут решениями исходного уравнения.

В некоторых случаях алгебраическую задачу (даже если в её условиях не содержится радикалов) с помощью специальных тригонометрических подстановок бывает целесообразно свести к тригонометрической задаче, и далее уже решать её методами тригонометрии.

Пример №352.

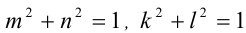
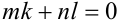
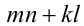
Известно, что и . Чему равно значение ?

Решение:

Воспользуемся тем, что если два действительных числа X, у удовлетворяют равенству

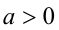
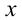
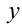
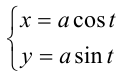
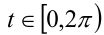
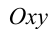
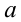
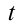
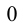
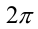
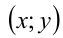
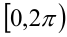
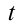
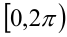
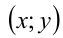
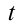
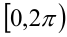
где — заданное число, то и можно представить в тригонометрическом виде , где . В самом деле, уравнение (1) задаёт на плоскости окружность радиуса с центром в начале координат. При изменении от до точка с координатами ровно один раз обходит окружность, и таким образом между точками окружности и полуинтервалом оказывается установлено взаимно однозначное соответствие. Это означает, что каждому значению из соответствует единственная пара чисел , удовлетворяющих равенству (1), и наоборот, каждой паре чисел, удовлетворяющих (1), соответствует единственное значение из .

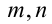
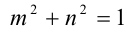
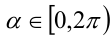
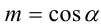
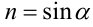
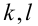
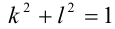
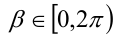
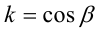
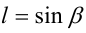
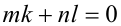
Итак, поскольку числа удовлетворяют равенству , то найдётся такое число , что , . Аналогично, поскольку числа удовлетворяют равенству , то найдётся такое число, что , . При этом условие примет вид

Выполнив тригонометрическую подстановку в искомом выражении 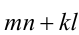, получим:

Введение новых переменных может быть вызвано необходимостью понизить степень уравнения, упростив при этом решение задачи.

Пример №353.

Решить уравнение

Решение:

Сведём данное уравнение 4-й степени к квадратному уравнению. Для этого вначале умножим обе части уравнения на 12 и приведём его к виду

Затем сделаем подстановку 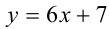, что приведёт к уравнению

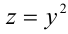
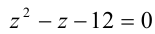
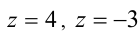
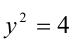
Сделав ещё одну подстановку , сведём окончательно данное биквадратное уравнение к квадратному уравнению , решив которое, находим корни . Тогда и

Ответ:

В следующем примере используется симметризирующая подстановка. Название говорит само за себя: уравнению придаётся более «симметричный» вид. Новая переменная является средним арифметическим входящих в уравнение выражений. При её применении уравнение 4-й степени общего вида приводится к более простому частному случаю, а именно, симметризация уравнения позволяет «убрать» из уравнения нечётные степени неизвестной, оставив только чётные и превратив его, таким образом, в биквадратное уравнение.

Пример №354.

Решение:

Выполним симметризирующую подстановку

Тогда уравнение примет вид

Ответ:

6.Близко к методу введения новых переменных стоит так называемый метод введения параметра. Не всегда введение параметра усложняет задачу. На примере, рассмотренном ниже, видно, как включение параметра в уравнение вместо числового коэффициента позволяет лучше «разглядеть» способ дальнейшего его решения — рассмотрение уравнения как квадратного относительно введённой величины.

Пример №355.

Решение:

Введём в уравнение параметр, положив :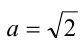

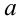
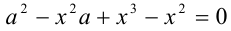
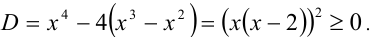
Рассмотрим теперь это уравнение как квадратное относительно . Приведём его к стандартному виду и вычислим дискриминант Найдём корни:

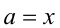
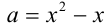
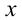
т.е. или . Параметр к этому моменту сыграл свою положительную роль, позволив свести решение кубического относительно уравнения к совокупности двух уравнений более низкой степени: квадратного и линейного.

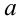
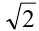
Заменяя числом , получим совокупность

Отсюда находим решения:

Замечание. В формуле корней квадратного уравнения более корректным было, вообще говоря, написать

Однако когда ищутся оба корня, то использование формул (1) и (2) приводит к одному результату. Именно поэтому часто в подобных ситуациях модуль опускают.

7.Отметим, что, вообще говоря, не всегда в задаче нужно полностью переходить к новым переменным. Иногда имеет смысл, вводя новую переменную, сохранить в задаче и первоначальную переменную, т.е. сделать частичную замену переменных. Так, сведением к системе уравнений, решаются некоторые уравнения. Рассмотрим в качестве пояснения пример.

Пример №356.

Решение:

Так как 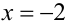не является корнем, то уравнение можно привести к равносильному виду

Положим 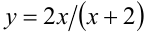, тогда уравнение сведётся к равносильной ему системе

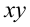
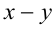
Решая эту систему относительно и , приходим к ответу:

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Алгебра

План урока:

Замена переменной

Пусть необходимо решить тригонометрическое уравнение

Это уравнение уже не является простейшим. Однако если заменить выражение 2х новой переменной (обозначим ее как t), то мы получим уже знакомое нам ур-ние:

Формула его корней выглядит так:

У нас есть формула, по которой можно вычислить значения t. Теперь произведем обратную замену:

Поделим это равенство на 2 и получим решение ур-ния:

Аналогичным путем можно решить любое уравнение вида

Где Т – какая-то тригонометрическая функция, k, b и a – некоторые числа.

Задание. Найдите решение тригонометрического уравнения

и выпишите его первые три положительных корня.

Решение. Введем переменную t = 3x + π/6, тогда ур-ние примет вид:

Далее следует обратная замена:

Получили формулу корней. Теперь надо найти три наименьших положительных корня. Напомним, что тригон-кое ур-ние имеет бесконечное количество корней, но каждый из них соответствует какому-либо целому числу n. Это соответствие как раз и задается формулой корней. Достаточно лишь выбрать какое-нибудь целое число n и подставить его в формулу корней. При этом большим значениям n соответствуют большие корни.

Выберем n = 0 и получим

Это положительный корень, но является ли он наименьшим? Проверим n = – 1:

Это отрицательное число. Значит, при n ≤– 1 получаются отрицательные корни, а при n ≥ 0 корни будут положительны. Нам нужны три наименьших положительных корня, им соответствуют значения n, равные 0, 1 и 2. Ноль мы уже подставляли в формулу корней, теперь подставим единицу и двойку:

Подставлять надо целые числа, потому что именно целым числам соответствуют корни уравнения. После формулы корней в ответах делается приписка «n∈ Z», или «где n – целое число».

Примечание. Записывая общее решение тригонометрических ур-ний (то есть серию корней), мы везде делаем приписку «n∊Z», которая означает, что n– это произвольное целое число. В будущем в промежуточных выводах мы ее делать не будем, так как она всегда подразумевается. Однако при решении учебных заданий, в том числе и на экзаменах, в ответе надо обязательно дописывать эту фразу, иначе оценка может быть снижена.

Заметим, что часто в простых случаях новую переменную не записывают явно, чтобы сделать решение более простым.

Задание. Решите ур-ние

Решение. Ур-ние cosx = – 1 является частным случаем, у которого решение записывается так:

Тогда для ур-ния cos (2x– π/4) = – 1 можно написать

Задание. Решите ур-ние

Решение. Слева стоит произведение двух скобок, а справа – ноль. Произведение будет равняться нулю лишь в том случае, когда хотя бы один из его множителей будет нулевым, то есть:

Вычислить arcsin 1/3 и arccos (– 2/5) мы не можем, так как чисел 1/3 и 2/5 нет в тригонометрических таблицах, поэтому оставляем решения в таком виде.

Теперь рассмотрим чуть более сложный случай, когда в качестве новой переменной принимают саму тригонометрическую функцию.

Задание. Решите уравнение методом замены переменной

Решение. Здесь за переменную можно принять величину sinx:

Получили обычное квадратное уравнение! Решим его, найдя дискриминант

У нас есть два значения t. Можно произвести обратную замену неизвестного:

Получили два тригонометрических уравнения. Второе из них решений не имеет, ведь область значений синуса – это промежуток [– 1; 1], то есть ни при каких х он не может быть равен двум. Решим первое уравнение:

Применение формул для преобразования уравнений

Когда в уравнении стоят различные тригонометрические функции, то замена одной из них переменной не помогает найти корни ур-ния. В таких случаях требуется использовать тригонометрические формулы, чтобы получилось ур-ние, содержащее только одну тригонометрическую функцию.

Задание. Решите ур-ние

Решение. В уравнении стоят две различные тригонометрические функции – синус и косинус. Следует упростить левую часть, чтобы в ней осталась только одна функция. Вспомним основное тригонометрическое тождество:

С его помощью можно выразить величину sin 2 x:

Теперь подставим эту формулу в исходное ур-ние:

Далее раскрываем скобки и приводим подобные слагаемые:

Получили обычное уравнение с заменой переменной. Из него с помощью замены t = cosx получаем квадратное ур-ние:

Производим обратную замену:

Каждое из этих ур-ний имеет решение. Начнем с первого из них:

Арккосинус от отрицательного числа найдем отдельно, используя формулу

Подставляем вместо а число 0,5:

Тогда решение ур-ния cosx = – 0,5 примет вид:

Теперь решим второе ур-ние:

Задание. Решите ур-ние

Решение. Перенесем все выражения в левую часть:

Можно заметить, что теперь в левой части стоит выражение, которое похоже на формулу синуса разности двух углов:

Действительно, если в формулу подставить значения α = 5х и β = 3х, то мы получим левую часть ур-ния. Это значит, что ур-ние можно переписать в виде:

Задание. Решите ур-ние

Решение. Сначала заменим синус двойного угла:

Далее вынесем за скобки множитель 2sinx:

В скобках осталось выражение, которое, согласно основному тригонометрическому тождеству, равно единице:

Задание. Решите ур-ние

Решение. Заменим cos2x, используя формулу косинуса двойного угла:

теперь избавимся от соs 2 x:

Вводим переменную t = sinx:

Выполняем обратную замену:

Запишем их решения:

Задание. Решите ур-ние

и укажите те корни, которые принадлежат промежутку [– 2π; – π].

Решение. Преобразуем обе части, используя формулу косинуса двойного угла, а также формулу приведения sin (x + π/2) = cosx:

И снова вводим новую переменную cosx = t:

Выполняем обратную замену

Так как arccos (– 0,5) = π – arccos 0,5 = π– π/3 = 2π/3, то решениями этих ур-ний будут серии:

Первая часть задания выполнена. Теперь следует отобрать корни, попадающие в промежуток [– 2π; – π]. Сначала для удобства разобьем первую серию решений на две:

Подставим в серии решений число n = 0:

Получили три корня, которые больше, чем (– π), а потому располагаются на координатной прямой правее промежутка [– 2π; – π].Значит, нет смысла проверять ещё большие значение n, ведь им будут соответствовать ещё большие значения х. Будем подставлять отрицательные значения n до тех пор, пока не получим корни, меньшие (– 2π). При n = – 1 имеем:

Корни х₁ и х₂ попадают в промежуток [– 2π; – π]. Теперь подставим n = – 2:

Все три полученных значения меньше, чем (– 2π), то есть они не входят в нужный нам промежуток. Нет смысла подставлять другие значение n (– 2, – 3, – 4 …), так как будут получаться ещё меньшие корни. В итоге только два корня, (– 4π/3) и (– 2π), принадлежат промежутку [– 2π; – π].

Иногда в ур-нии стоят тригонометрические функции от разных углов. В этом случае приходится использовать формулы суммы или разности аргументов.

Задание. Решите ур-ние

Решение. Разложим выражения sin (π/3 – х) и sin (π/6 – х), используя формулу синуса и косинуса разности:

Тогда левая часть ур-ния примет вид:

Здесь мы просто левую часть, в которой большое выражение стоит, заменяем

А то, что такую замену можно сделать, мы доказали в решении до этого, используя формулы разности.

Соответственно, всё уравнение можно переписать так:

Однородные тригонометрические уравнения

Особый интерес представляют уравнения вида

где а и b – некоторые постоянные числа, не равные нулю. Такие ур-ния называют однородными уравнениями 1-ой степени. Приведем несколько примеров таких ур-ний:

Для решения таких ур-ний обе части делят на cosx:

Обратите внимание, что при выводе этой формулы мы делили ур-ние на cosx. Однако это выражение может быть равным нулю, а деление на ноль запрещено. Это значит, что мы должны быть уверены, что у ур-ния нет такого корня х, что соs х = 0. Уверены ли мы в этом?

Заметим сразу, что функции у = sinx и у = cosx обращаются в ноль в различных точках. Поэтому, если сosx = 0, то sinx ≠ 0, а значит, и всё выражение

не равно нулю. Поэтому мы можем спокойно делить такое ур-ние на соsx.

Задание. Решите ур-ние

Решение. Делим обе части на соsх и получаем:

Задание. Решите ур-ние

Решение. Можно составить две формулы приведения:

С их учетом исходное ур-ние примет вид:

Делим ур-ние на cos 2x:

Существуют и более сложные однородные уравнения второй степени. В общем случае они имеют вид:

Для того, чтобы решить их, необходимо поделить обе части на cos 2 x, и тогда мы получим равносильное ур-ние:

Произведя замену tgx = t, получим квадратное уравнение

Задание. Решите ур-ние

Решение. Поделим обе части на выражение cos 2 x:

Введем переменную tgx = t:

Возвращаемся к переменной х:

Введение вспомогательного угла

В правой части однородного ур-ния стоит ноль. Усложним задачу и рассмотрим схожие ур-ния, у которых справа стоит произвольное число, которое может быть и отлично от нуля. То есть ур-ние имеет вид

Существует ли универсальный метод решения тригонометрических уравнений такого вида? Да, существует, и называется он методом вспомогательного угла. Очевидно, что величина a 2 + b 2 является положительной, ведь это сумма квадратов чисел, отличных от нуля. Это значит, что существует действительное число

которое больше нуля.

Поделим ур-ние на N и получим новое ур-ние

Для краткости введем новые обозначения:

коэффициенты уравнения запишем большими буквами, чтобы не писать корни.

и тогда ур-ние примет более простой вид:

Попытаемся найти величину А 2 + В 2 :

Так как величина А 2 + В 2 равна единице, то можно подобрать такой угол α, что будут одновременно выполняться равенства

Угол α называют вспомогательным углом. Как его подобрать? Из равенства А = sinα очевидно, что

Заменим в (1) числа А и В по формулам (2) и (3) и получим:

Теперь слева стоит косинус разности, который можно «свернуть»:

Это уже почти что простейшее тригонометрическое уравнение, которое мы сможем решить.

Задание. Решите ур-ние

Решение. Коэффициенты перед синусом и косинусом равны 5 и 12. Найдем корень из суммы 5 2 + 12 2 :

Значит, число N = 13. Поделим ур-ние на 13:

Теперь введем вспомогательный угол α = arcsin 5/13. Тогда

Подставим в (1) вместо дробей 5/13 и 12/13 sinα и cosα:

Теперь смотрим в тригонометрические формулы сложения и вычитания аргументов. Есть ли там что-то похожее на левую часть ур-ния? Действительно, там есть следующая формула:

Наше ур-ние похоже на эту формулу, но надо поменять местами вычитаемое и уменьшаемое. Для этого можно умножить ур-ние на (– 1):

Уравнения с ограничениями на значение переменной

До этого мы рассматривали случаи, при которых переменная х могла принимать любые значения в уравнении. Однако, если в ур-нии переменная стоит под знаком корня или находится в знаменателе, то возникают некоторые ограничения на те значения, которые она может принимать. Рассмотрим пример.

Задание. Решите ур-ние

Решение. В левой части произведение двух множителей, а справа – ноль, следовательно, можно записать:

Решение для первого уравнения запишем в виде двух серий, а не одной (так проще будет проводить дальнейшее исследование). Сначала вычислим арксинус:

Тогда получаем три серии решений:

Теперь учтем, что в исходном уравнении выражение cosx стоит под корнем, поэтому должно соблюдаться условие:

Косинус принимает положительные значения в I и IV четверти. Отметим все серии решении на единичной окружности и посмотрим, какие из них попадают в I и IV четверть:

Теперь мы видим, что корни из серии 4π/3 + 2πn находятся в III четверти, то есть для них соsx 2 x = ctgx