Уравнения системы по временной области

Описание линейной дискретной системы во временной области

3.1.2.1. Импульсная и переходная характеристики ЛДС

Во временной области линейная дискретная система (ЛДС) описывается импульсной характеристикой.

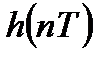
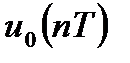
Импульсной характеристикой ЛДС называется ее реакция на единичный дискретный импульс при нулевых начальных условиях: рисунок 2.

Рисунок 2.1 – определение импульсной характеристики ЛДС

Единичный дискретный импульс описывается соотношением:

(2.1)

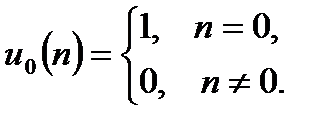
Импульсная характеристика 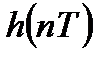является основной характеристикой линейной дискретной системы, так как с ее помощью легко определяется реакция на произвольное входное воздействие.

При описании ЛДС во временной области кроме импульсной характеристики используют переходную характеристику.

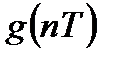
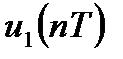
Переходной характеристикой ЛДС называют ее реакцию на единичный дискретный скачок при нулевых начальных условиях: рисунок 3.

Рисунок 2.2 – определение переходной характеристики ЛДС

Единичный дискретный скачок описывается соотношением:

(2.2)

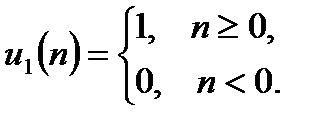
3.1.2.2. Связь выходного сигнала ЛДС с входным во временной области

Во временной области соотношение вход-выход ЛДС описывается линейными уравнениями:

— формулой свертки при использовании импульсной характеристики;

— разностным уравнением, если используются параметры ЛДС.

Формула линейной свертки

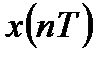
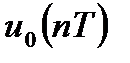
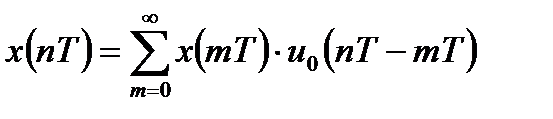
Для получения уравнения свертки представим любой дискретный сигнал в виде линейной комбинации единичных дискретных импульсов :

.

Воспользовавшись свойствами аддитивности и определением импульсной характеристики линейной дискретной системы, можно получить уравнение свертки:

. (2.3)

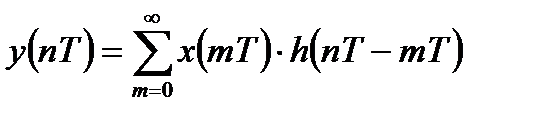
В результате замены переменных можно получить второй вариант записи формулы свертки:

. (2.4)

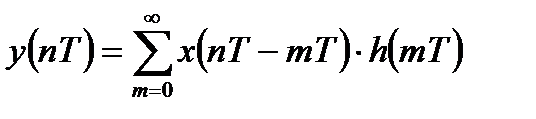
Стандартное условное обозначение операции свертки имеет следующий вид:

.

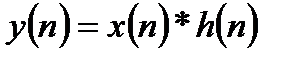
В общем случае ЛДС суммирует с некоторыми весовыми коэффициентами не только некоторое количество входных отсчетов, но и некоторое количество предшествующих выходных отсчетов:

, (2.5)

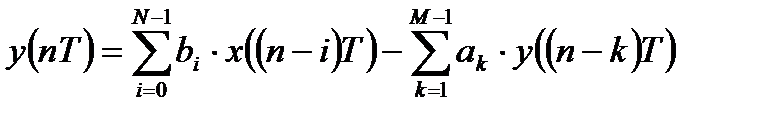
где 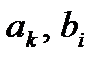— коэффициенты разностного уравнения.

Данная форма разностного уравнения иногда называется алгоритмом дискретной фильтрации. Если в левой части уравнения разместить только выходные отсчеты, а в правой части только входные, то получают форму записи, которую называют классическим разностным уравнением:

. (2.6)

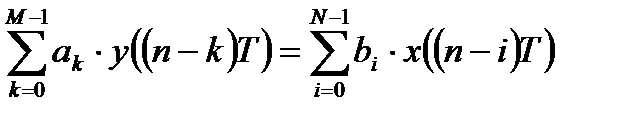
Разностное уравнение является аналогом дифференциального уравнения аналоговой линейной системы для линейных дискретных систем.

. (2.7)

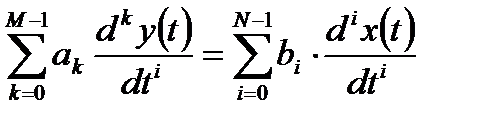
Переход дифференциального уравнения к дискретному аналогу в виде разностных уравнений может быть произведен путем замены производных конечными разностями:

; (2.8)

. (2.9)

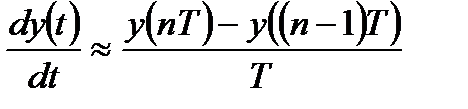
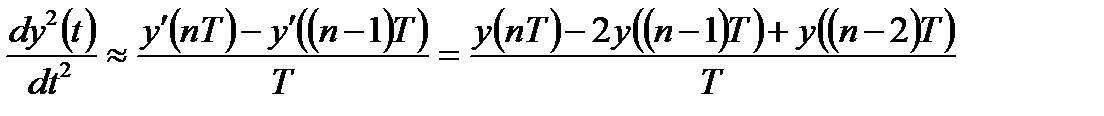
Вычисление выходного сигнала аналоговой системы может быть получено только приближенно путем замены операции интегрирования в интеграле Дюамеля одним из методов численного интегрирования. В то же время разностное уравнение или алгоритм дискретной фильтрации представляют собой алгоритм непосредственного вычисления выходного сигнала методом прямой подстановки при известном входном воздействии и предшествующих значениях выходного сигнала (реакции).

3.1.3. Описание линейной дискретной системы в Z – области

Математический аппарат z – преобразования, подобно преобразованию Лапласа в теории линейных аналоговых цепей, существенно упрощает анализ ЛДС.

Передаточная функция ЛДС

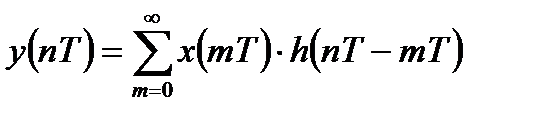
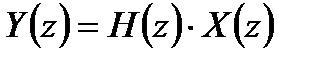
Применим z – преобразование к уравнению дискретной линейной свертки . В соответствии со свойствами z – преобразования получим:

, (3.1)

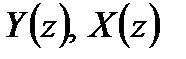
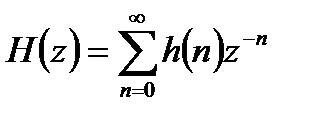
где — z – преобразования реакции и воздействия;

— z – преобразование импульсной характеристики.

Функция, представляющая собой z – преобразование импульсной характеристики

(3.2)

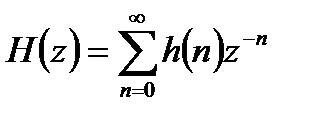
называется передаточной функцией (системной функцией) ЛДС.

Передаточная функция также может быть представлена и следующим образом:

. (3.3)

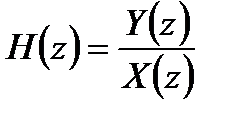
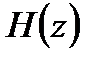
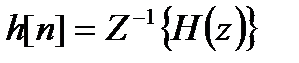
При известном изображении импульсная характеристика находится с помощью обратного z – преобразования:

. (3.4)

Таким образом, передаточная ЛДС – это отношение z – преобразования реакции к z – преобразованию воздействия.

Связь передаточной функции с разностным уравнением

Применим z – преобразование к разностному уравнению

.

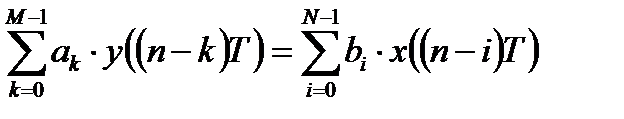
В этом случае, учитывая свойство z – преобразования по запаздыванию воздействия, можно получить передаточную функцию ЛДС общего вида:

. (3.5)

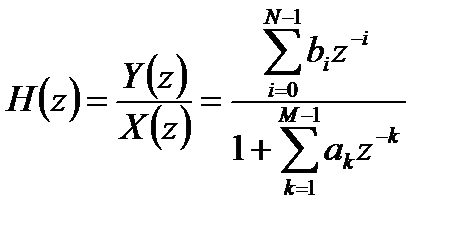
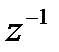
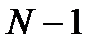
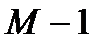
Таким образом, передаточная функция ЛДС представляет собой дробно-рациональную функцию, числитель и знаменатель которой дееются многочленами аргумента порядков и с вещественными коэффициентами.

Как любая дробно-рациональная функция, передаточная функция ЛДС характеризуется полюсами и нулями.

Нулями называют значения 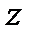, при которых передаточная функция равна нулю.

Полюсами называют значения 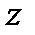, при которых знаменатель передаточной функции равен нулю.

Разновидности передаточных функций

Кроме передаточной функции общего вида, существуют другие формы записи передаточной функции.

Одна из эквивалентных форм записи передаточной функции выглядит следующим образом

, (3.6)

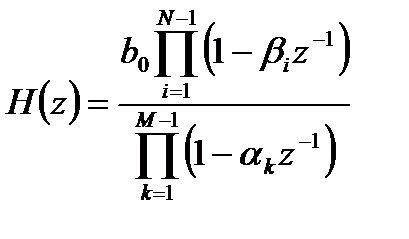
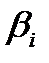
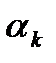
где — нули, — полюса.

Нули и полюса передаточной функции могут быть либо вещественными, либо составлять комплексно-сопряженные пары. Коэффициент усиления 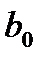всегда вещественный.

Возможен третий вариант представления передаточной функции в виде суммы простых дробей ( :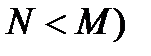

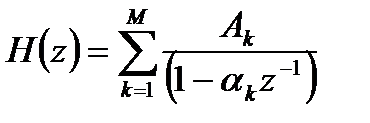
, (3.7)

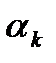
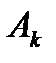
где — полюс;

— коэффициент разложения при k-м полюсе.

Оценка устойчивости ЛДС по ее передаточной функции

Представление функции передачи в виде суммы простых дробей позволяет найти импульсную характеристику системы через обратное z – преобразование, так как каждому слагаемому выражения (3.7) соответствует обратное преобразование вида :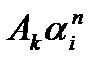

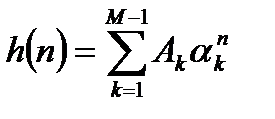
. (3.8)

Таким образом, ряд будет сходиться и ЛДС будет устойчива, если выполняется условие:

(3.9)

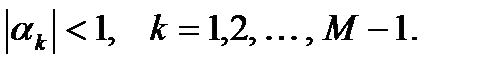
Таким образом, для того, чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюса ее передаточной функции распределялись внутри единичного круга комплексной z-плоскости.

Курсовая работа: Анализ цепи во временной области различными методами

Содержание

1. Введение

3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях

3.1 Составление уравнений состояния цепи.

3.2 Определение точных решений уравнений. Решение уравнений состояния численным методом

4. Анализ цепи операторным методом при апериодическом воздействии.

4.1 Определение функции передачи, её нулей и полюсов

4.2 Определение переходной и импульсной функции

4.3 Определение напряжения через нагрузку

5. Анализ цепи частотным методом при апериодическом воздействии.

5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик функции передачи

5.2 Определение амплитудного и фазового спектра входного сигнала

5.3 Определение амплитудного и фазового спектра выходного сигнала

5.4 Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина

6. Анализ цепи частотным методом при периодическом воздействии

6.1 Разложение в ряд Фурье периодической функции и определение её амплитудного и фазового спектров

6.2 Определение напряжения через нагрузку

8. Список используемой литературы.

Практическое применение расчета электрических цепей очень важно. В курсовой работе требуется провести анализ линейной разветвленной электрической цепи различными методами.

Целью курсовой работы является овладение некоторыми современными методами анализа линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники.

В курсовой работе использован следующий материал курса теоретических основ электротехники: методы расчёта сложных цепей, анализ цепей во временной области, операторный метод анализа цепей, частотный метод анализа цепей.

При выполнении курсовой работы применялась программа MathCAD Profession , что позволило значительно упростить вычисления и расчёты в ряде случаев.

2. Постановка задачи

На рисунке 1 представлена анализируемая цепь. Параметры элементов цепи следующие: , , , , , , , . Здесь — единичная ступенчатая функция (функция включения). Параметры одиночного и последовательности импульсов: , , . График одиночного импульса приведён на рисунке 1.1.

Рисунок 1. Схема анализируемой цепи.

Рисунок 1.1. Входной импульс.

3. Анализ цепи во временной области методом переменных состояния при постоянных воздействиях

3.1 Составление уравнений состояния цепи

Уравнения электромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.Количество переменных состояния, следовательно, число уравнений состояния равно числу независимых накопителей энергии.

В данной задаче переменными состояния являются напряжения на ёмкостях и ток в индуктивности: и . При этом переменные состояния образуют систему из наименьшего числа переменных, полностью определяющих реакции всех ветвей цепи при заданных начальных условиях и приложенных при внешних воздействиях.

Требуемая система уравнений может быть получена из системы уравнений, составленной по законам Кирхгофа. При этом целесообразно записывать напряжения и токи на емкости и индуктивности через переменные состояния.

Выберем направления токов (рисунок 2).

Рисунок 2. Выбор направлений токов в ветвях и контуров.

Составим уравнения по законам Кирхгофа:

Исключив из уравнений токи и напряжения, не связанные с переменными состояния, получим систему уравнений по методу переменных состояния, разрешенную относительно первых производных (форма Коши):

(1)

В матричной форме записи эта система имеет вид:

, (2)

где матрица коэффициентов при переменных состояния,называемая матрицей Якоби; — вектор — столбец переменных состояния; — матрица коэффициентов источников тока и э.д.с.; — вектор — столбец параметров источников.

В нашем случае это:

3.2 Определение точных решений уравнений состояния

Решение системы (1) определяется выражением:

Так как в цепи действуют источники постоянной ЭДС Е и постоянного тока J, то решение может быть представлено в более простом виде:

, (3)

Здесь — матричная экспоненциальная функция; — вектор-столбец начальных значений переменных состояния; — единичная матрица.

Начальные значения переменных состояния могут быть определены из анализа схемы до коммутации. Предполагается, что в схеме до коммутации существовал установившийся режим постоянного тока, что позволяет представить схему в виде:

Рисунок 2.1. Схема определения независимых начальных условий.

Анализ схемы рис. 2.1 позволяет определить независимые начальные условия:

(4)

Для определения матричной экспоненциальной функции используем разложение в ряд Тейлора:

, (5)

Число членов разложения должно быть равно числу переменных состояния. и являются некоторыми функциями времени, которые в свою очередь находятся из системы:

(6)

Найдя собственные значения матрицы :

подставляем их в (6) и находим и :

3.3 Решение уравнений состояния численным методом

Решение системы уравнений (1) может быть найдено с помощью какого-либо численного метода интегрирования дифференциальных уравнений. В этих методах интересующий промежуток разбивается на равные малые интервалы h. Приближённые дискретные значения переменных состояния определяются последовательно, на каждом шаге, начиная от времени t = 0 .

Решение системы (1) с использованием явного метода Эйлера (или алгоритма Рунге-Кутта первого порядка) имеет вид:

Начальным значениям переменных состояния соответствует k = 0. Оценить временной интервал Dt _расч расчета можно на основе известных собственных значений матрицы как Dt _расч = 4/ |l _min |. Здесь |l _min | — минимальное собственное значение, если собственные значения являются вещественными, отрицательными и различными, или вещественная часть комплексного собственного значения, если собственные значения являются комплексно сопряженными. Тогда шаг расчета может быть найден исходя из выражения: h = Dt _расч / N . N — число шагов, на которые разбит интервал Dt _расч .Положим N =80 , тогда h = 2,25*10 -6 . Погрешность расчёта пропорциональна h 2 .

Таблица значений переменных состояния на каждом шаге.

U,B I, A

— аналитическое решение

— численное решение

Рисунок 2.2 Изменение напряжения на конденсаторе С₄

— аналитическое решение

— численное решение

Рисунок 2.3 Изменение тока в катушке индуктивности L₃

4. Анализ цепи операторным методом при

4.1 Определение функции передачи, её нулей и полюсов

Анализу подлежит схема представленная на рис. 3. Начальные условия в цепи нулевые, в момент t = 0 на вход цепи источником напряжения подан импульс (рисунок 1) с амплитудой 10 В и длительностью 60 мкс., j ( t ) = 0.

Рисунок 3.Операторная схема замещения.

Составим уравнения в операторной форме по законам Кирхгофа, найдём отношение . Это отношение является функцией передачи .

Таким образом, функция передачи будет иметь вид:

(7)

Полюсы функции передачи могут быть найдены путём нахождения корней полинома второй степени, находящегося в знаменателе самой функции:

Совпадение полюсов функции передачи и с собственными значениями матрицы — и даёт дополнительную информацию о правильности нахождения передаточной функции.

Аналогично из числителя функции передачи находятся нули функции:

Наиболее наглядным способом охарактеризовать передаточную функцию является графическое расположение ее полюсов и нулей на комплексной плоскости, называемой диаграммой полюсов-нулей (рис.3.1).

Рисунок 3.1. Диаграмма полюсов-нулей.

Так как полюсы передаточной функции лежат в левой полуплоскости, в линейной пассивной цепи имеются резистивные элементы, в результате чего будет происходить затухание свободной составляющей напряжения. Передаточные функции, полюса которых не лежат в правой полуплоскости комплексной плоскости, называются устойчивыми.

Нули передаточной функции при учете потерь могут располагаться в любой части комплексной плоскости.

4.2 Определение переходной и импульсной характеристик

Переходная характеристика цепи представляет собой реакцию цепи на воздействие единичной ступенчатой функции (функции Хэвисайда 1 (t) ) и может быть найдена как обратное преобразование Лапласа от, либо с помощью формулы разложения:

, (8) где и числитель и знаменатель передаточной функции соответственно, а — корни выражения :

Таким образом, подставляя корни и, применяя преобразование Эйлера, получим:

Импульсная характеристика цепи представляет собой реакцию цепи на воздействие единичной импульсной функции и может быть найдена как обратное преобразование Лапласа от передаточной функции, либо с помощью формулы разложения:

, (9) где и числитель и знаменатель передаточной функции соответственно, а — полюсы :

Первое слагаемое определяется действием на входе цепи d — импульса тока и существует только для t=0 . В дальнейшем переходной процесс протекает за счет энергии, накопленной в электрическом поле конденсатора и магнитном поле индуктивности в результате действия d — импульса тока. Из приведенного выражения видно, что, как и в первом случае, переходной процесс носит затухающий колебательный характер с частотой, равной собственной частоте рассматриваемой цепи: w _св = 41574 рад/сек.Подобного вида решения (с d -функцией) возникают всякий раз, когда степени полиномов числителя и знаменателя передаточной функции оказываются равными. Коэффициент при соответствует части входного импульса поступающей в нагрузку.

Рисунок 3.2. Импульсная и передаточная характеристики

4.3 Определение напряжения на нагрузке

Входной импульс в данном задании представляет собой знакопеременное прямоугольное напряжение. Его можно представить как сумму следующих функций:

Применяя теорему Запаздывания, найдём операторное изображение для одиночного импульса напряжения:

(10)

Так как , выразим :

(11)

Подставив в (11) выражения (10) и (7), получим:

Для того чтобы найти оригинал этой функции, воспользуемся таблицами для преобразований Лапласа:

Рисунок 3.3 Графики входного и Рисунок 3.4 График выходного

выходного сигналов сигнала

5. Анализ цепи частотным методом при апериодическом воздействии

5.1 Определение амплитудно-фазовой (АФХ), амплитудно-частотной (АЧХ)и фазо-частотной (ФЧХ) характеристик функции передачи

Амплитудно-частотная характеристика – это зависимость от частоты модуля входной, выходной или передаточной функции цепи, выраженных в комплексной форме (ГОСТ 19880-74 ). Амплитудно-частотная характеристика (АЧХ) является одной из самых важных характеристик любой цепи и позволяет исследовать искажения вносимые цепью в спектр входного сигнала. Наличие частотно — зависимых элементов (L и C ) в исследуемой цепи приводит к неравномерному изменению составляющих спектра входного сигнала. Наиболее простой способ получения АЧХ цепи — это замена в выражении для операторной переменной p на мнимую частоту jw и нахождение модуля полученной комплексной функции частоты:

Рисунок 4.1 АЧХ функции передачи по напряжению

Характеристика имеет вид, качественно сходный с подобной характеристикой параллельного колебательного контура. По построенной характеристике может быть определена полоса пропускания. Полоса пропускания – полоса частот, в пределах которой затухание остаётся ниже определённого значения (СТ МЭК 50(151)-78 ). Т. е. коэффициент передачи для этой полосы не более чем в отличается от его максимального значения. Для рассматриваемой цепи максимальное значение передаточной функции достигается на нулевой частоте (для постоянного напряжения) и составляет . Границе полосы пропускания соответствует значение передаточной функции . Это значение достигается на частоте . Таким образом, полоса пропускания равна: .

Фазо-частотная характеристика – зависимость от частоты аргумента входной, выходной или передаточной функций цепи, выраженных в комплексной форме (ГОСТ 19880-74 ). Таким образом, для данной цепи ФЧХ будет иметь вид: . Построенная по данному выражению ФЧХ имеет вид, представленный на рис. 4.2.

Рисунок 4.2 ФЧХ функции передачи по напряжении

Амплитуднофазочастотная характеристика цепи (годограф) связывает воедино изменение коэффициента передачи (в нашем случае, по напряжению — ) и фазового сдвига между выходным и входным напряжением во всем диапазоне частот. Годограф включает сведения, которые содержатся как в АЧХ, так и в ФЧХ.

Рисунок 4.3 Годограф анализируемой цепи

Годограф является параметрической кривой, параметром которой является частота w . Длина вектора, проведенного из начала координат к какой-либо точке годографа, соответствует абсолютному значению передаточной функции на этой частоте , а угол между ним и положительным направлением вещественной оси — аргументу передаточной функции . Нулевой частоте (постоянному напряжению) соответствует точка с координатой 0.1428 на вещественной оси, очень большой (в пределе бесконечной) частоте соответствует точка с координатой 0.09524 на вещественной оси. На этих граничных частотах влияние реактивных элементов на фазовый сдвиг отсутствует.

5.2 Определение амплитудного и фазового спектра входного сигнала

Для нахождения спектральной характеристики входного сигнала можно воспользоваться непосредственно прямым преобразованием Фурье. Второй путь решения этой задачи основан на аналогии между преобразованиями Лапласа и Фурье и состоит в замене в операторном изображении входного сигнала (10) операторной переменной p на мнимую частоту jw . В итоге после простых преобразований получим:

Амплитудный спектр входного сигнала может быть найден как модуль спектральной характеристики сигнала:

Рисунок 4.4 АЧХ входного сигнала

Максимальное значение спектральной характеристики достигается при и составляет . Определенная по уровню ширина спектра сигнала составляет . Между шириной спектра сигнала и его длительностью существует следующее соотношение: . Для данного вида сигнала получаем: . Эта константа называется базой сигнала. Уменьшение длительности импульса в 100 раз приводит к такому же (в 100 раз) увеличению ширины его спектра. Наличие широкого спектра у коротких импульсов дает возможность использования таких импульсов для исследования частотных свойств различных цепей. В математическом смысле спектр несинусоидального сигнала неограничен.

Фазовый спектр входного сигнала определяется как аргумент от входной спектральной характеристики: .

Рисунок 4.5 Фазовый спектр входного сигнала

5.3 Определение амплитудного и фазового спектра выходного сигнала

Амплитудно-частотная характеристика выходного сигнала может быть получена перемножением амплитудно-частотных характеристик входного сигнала и цепи : .

График АЧХ выходного сигнала приведён на рис. 4.6.

Рисунок 4.6 Амплитудно-частотная характеристика

входного сигнала

Сравнение АЧХ с соответствующей характеристикой позволяет предположить значительное искажение формы выходного сигнала. Искажения связаны с различием величины передаточной функции для различных составляющих спектра входного сигнала. Для резистивной цепи выходной сигнал был бы подобен входному и имел бы ту же длительность. В данном случае цепи содержащей частотнозависимые элементы значительные изменения будут иметь место и для фазового спектра входного сигнала. Это приведет к нарушению фазовых соотношений между составляющими сигнала и станет другой причиной искажения формы выходного сигнала. Искажение на рис. 4.6 и рис. 4.7 ярко выражено на частоте , т. е. той же частоте, что имела место в АЧХ функции передачи по напряжению(рис. 4.1), определяющей характеристику данной цепи как параллельного колебательного контура. Анализ преобразования импульсного сигнала основывается на представлении о том, что искажение фронта выходного импульса по сравнению с формой входного импульса зависит от свойств цепи на высоких частотах (теоретически на бесконечно высоких частотах). Искажение формы вершины импульса определяется свойствами цепи на низких частотах. Используя подобный подход, например, для анализа искажений фронта входного импульса «закорачивают» конденсаторы, находящиеся на пути следования сигнала в нагрузку и заменяют разрывом индуктивные элементы, включенные параллельно резистивным элементам схемы.

Фазовый спектр выходного сигнала может быть получен суммированием аргумента спектральной характеристики и ФЧХ цепи:

Рисунок 4.7 Фазовый спектр выходного сигнала

5.4 Определение выходного сигнала по вещественной характеристике при помощи приближенного метода Гиллемина

Метод Гиллемина является одним из методов позволяющих восстановить функцию времени (какой — либо сигнал) по известной вещественной (или мнимой) частотной характеристике. Метод основан на такой аппроксимации, когда аппроксимирующая частотную характеристику функция либо ее производные состоят из последовательности бесконечно коротких импульсов. Последовательность бесконечно коротких импульсов представляет собой заданную функцию в так называемой квантованной форме. Погрешность метода преимущественно связана со ступенчатым характером аппроксимирующей функции. Уменьшение этой погрешности требует увеличения общего числа членов в аппроксимации. Исходная частотная характеристика аппроксимируется кусочнолинейным образом, после чего два последовательных дифференцирования позволяют свести аппроксимирующую функцию к последовательности бесконечно коротких импульсов. Окончательное выражение для искомой функции времениf ( t ) полученной по вещественной частотной характеристике имеет вид:

(12)

Здесь a_k — величины бесконечно коротких импульсов, w_k — координаты импульсов на частотной оси. Вещественная частотная характеристика может быть определена из соотношений: ; ; , где — фазо-частотная характеристика цепи, — фазо-частотная характеристика входного сигнала.

Рисунок 4.8 Аппроксимация вещественной частотной характеристики

Аппроксимация позволяет найти точки , необходимые для записи и построения первой производной вещественной частотной характеристики :

Рисунок 4.9 Первая производная —

На этом шаге уже можно восстановить функцию времени (). Для этого воспользуемся выражением вида:

Аналогично вычисляется вторая производная вещественной частотной характеристики :

Рисунок 4.11 Вторая производная —

Применяя выражение (12), можно восстановить выходной сигнал :

Рисунок 4.12 Аппроксимированный выходной сигнал по

6. Анализ цепи частотным методом при периодическом воздействии

6.1 Разложение в ряд Фурье заданной периодической функции, определение амплитудного и фазового спектров

Разложение периодической последовательности импульсов может быть осуществлено с учетом очевидной связи комплексной амплитуды гармоники ряда Фурье и спектральной плотности одиночного импульса той же формы . Коэффициенты ряда Фурье могут быть найдены по формуле:

Фазовые коэффициенты определяются как аргумент комплексного числа :

Амплитуда k — той гармоники

Рисунок 5.1 Амплитудный спектр входного сигнала

На рис. 5.1 представлен амплитудный спектр входного сигнала. Огибающая дискретного спектра периодического сигнала совпадает с амплитудно-частотной характеристикой одиночного импульса. При всех частотах амплитуды спектра периодической функции отличаются от значений спектральной плотности непериодической только постоянным множителем . Увеличение периода следования импульсов ведет к уменьшению расстояния между соседними гармониками амплитудного спектра. При увеличении периода до бесконечности дискретный амплитудный спектр периодической последовательности переходит в непрерывный спектр одиночного импульса. Вид этого спектра наглядно позволяет судить о свойствах периодических функций времени, например, по скорости уменьшения амплитудного спектра можно судить о степени гладкости периодической функции, а по наличию или отсутствию гармоник на высоких частотах – есть ли участки с быстрыми изменениями. Амплитудный спектр является четной функцией частоты, а фазовый – нечетной функцией.

Рисунок 5.2 Фазовый спектр входного сигнала

Таким образом, входной сигнал можно представить как

6.2 Определение напряжения на нагрузке

Для определения коэффициентов ряда Фурье выходного тока вычислим значения АЧХ и ФЧХ функции передачи, полученной нами в пункте 4.1, для значений ( k × w 1) ,k =0,1,2,3. 14. Тогда:

Амплитуда k — той гармоники

Заданная периодическая последовательность импульсов

Аппроксимация отрезком ряда Фурье

Напряжение на выходе цепи

Аппроксимация отрезком ряда Фурье

В данной курсовой работе были применены различные современные методы для анализа разветвлённой линейной электрической цепи при различных воздействиях в переходном и установившемся режимах с применением вычислительной техники.

Вычисления, проводимые с помощью математического пакета MathCAD Profession , в большинстве случаев были проверены встроенными функциями, согласующимися с поставленной задачей в данной курсовой работе.

Анализ графиков показывает, что характер их изменения весьма соответствует характеру физической реализации цепи с данным включением L и С элементов.

Применяемые аппроксимации в качестве дополнительной информации о правильности, в результате подтвердили выполненные расчёты.

8. Список используемой литературы

1. Бессонов Л.А. Теоретические основы электротехники. — М.: Высшая школа, 1996.

2. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. — М.: Высшая школа, 1990.

3. Зевеке Г.В. и др. Основы анализа цепей. — М.: Энергоатомиздат, 1989. 5-е изд. — 528.

4. Лосев А.К. Теория линейных электрических цепей. – М: Высшая школа, 1987.

5. Шебес М.Р. Каблукова М.В. Задачник по теории линейных электрических цепей. –М: Высшая школа, 1990.

6. Зевеке Г.В. и др. Основы анализа цепей. — М.: Энергоатомиздат, 1975. 4-е изд. — 752

Пространство состояний в задачах проектирования систем оптимального управления

Введение

Исследование системы управления во временной области с помощью переменных состояния широко используется в последнее время благодаря простоте проведения анализа.

Состоянию системы соответствует точка в определённом евклидовом пространстве, а поведение системы во времени характеризуется траекторией, описываемой этой точкой.

При этом математический аппарат включает готовые решения по аналоговому и дискретному LQR и DLQR контролерам, фильтра Калмана, и всё это с применением матриц и векторов, что и позволяет записывать уравнения системы управления в обобщённом виде, получая дополнительную информацию при их решении.

Целью данной публикации является рассмотрение решения задач проектирования систем оптимального управления методом описания пространства состояний с использованием программных средств Python.

Теория кратко

Векторно-матричная запись модели линейного динамического объекта с учетом уравнения измерения принимает вид:

(1)

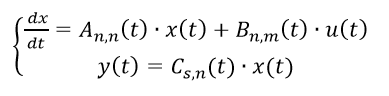
Если матрицы A(t), B(t) и C(t) не зависят от времени, то объект называется объектом с постоянными коэффициентами, или стационарным объектом. В противном случае объект будет нестационарным.

При наличии погрешностей при измерении, выходные (регулируемые) сигналы задаются линеаризованным матричным уравнением:

(2)

где y(t) – вектор регулируемых (измеряемых) величин; C(t) – матрица связи вектора измерений с вектором состояний; v(t) – вектор ошибок измерений (помехи).

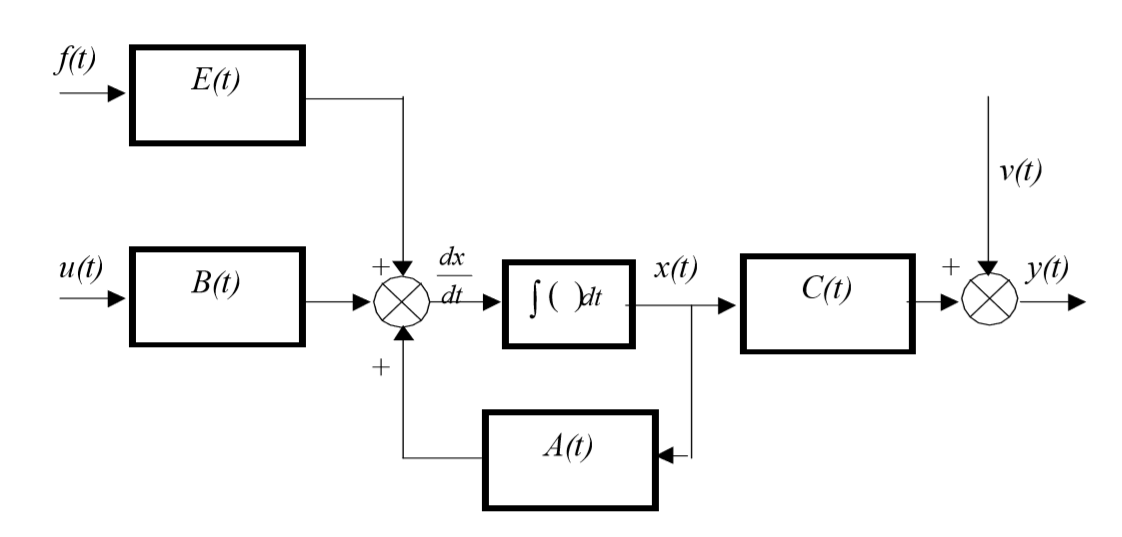
Структура линейной непрерывной системы, реализующая уравнения (1) и (2), приведена на рисунке:

Данная структура соответствует математической модели объекта, построенной в пространстве состояний его входных x(t), u(t), выходных y(t) и внутренних, или фазовых координат x(t).

Для примера рассмотрим математическую модель двигателя постоянного тока с независимым возбуждением от постоянных магнитов. Система уравнений электрической и механической частей двигателя для рассматриваемого случая будет выглядеть так:

(3)

Первое уравнение отражает взаимосвязь между переменными в цепи якоря, второе — условия механического равновесия. В качестве обобщенных координат выберем ток якоря I и частоту вращения якоря ω.

Управлением являются напряжение на якоре U, возмущением — момент сопротивления нагрузки Mc. Параметрами модели являются активное сопротивление и индуктивность цепи и якоря, обозначенные соответственно Rя, и Lя, а также приведенный момент инерции J и конструктивные постоянные се и см (в системе СИ: Cе=См).

Разрешая исходную систему относительно первых производных, получим уравнения двигателя в пространстве состояний.

(4)

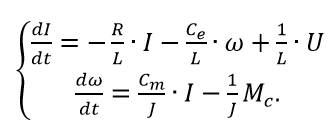
В матричном виде уравнения (4) примут вид (1):

(5)

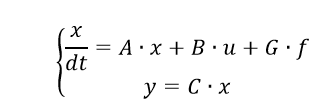
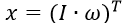
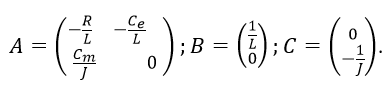
где вектор обобщенных координат , вектор управлений U =u (в рассматриваемом случае он является скаляром), вектор (скаляр) возмущений Mc=f. Матрицы модели:

(6)

Если в качестве регулируемой величины выбрать частоту вращения, то уравнение измерения запишется в виде:

(7)

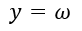
а матрица измерений примет вид:

Сформируем модель двигателя в Python. Для этого вначале зададим конкретные значения параметров двигателя: U = 110 В; R =0,2 Ом; L = 0,006 Гн; J =0,1 кг/м2;Ce =Cm=1,3 В/С и найдем значения коэффициентом матриц объекта из (6).

Разработка программы формирующей модель двигателя с проверкой матриц на наблюдаемость и управляемость:

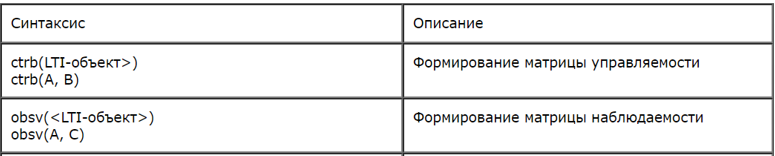
При разработке программы использовалась специальная функция def matrix_rank для определения ранга матрицы и функции, приведенные в таблице:

Результаты работы программы:

Матрица А:
[[ -33.33333333 -216.66666667]
[ 13. 0. ]]
Матрица B:
[[166.66666667]
[ 0. ]]
Матрица C:
[[0 1]]
Скаляр D:
0
Передаточная функция двигателя:
2167/(s^2 + 33.33 s + 2817)
Ранг матрицы управляемости: 2
Ранг матрицы наблюдаемости: 2

1. На примере двигателя постоянного тока с независимым магнитным возбуждением рассмотрена методика проектирования управления в пространстве состояний;

2. В результате работы программы получены передаточная функция, переходная характеристика, а так же ранги матриц управляемости и наблюдаемости. Ранги совпадают с размерностями пространства состояний, что подтверждает управляемость и наблюдаемость модели.

Пример проектирования оптимальной системы управления с дискретным dlqr контролером и полной обратной связью

Определения и терминология

Линейно-квадратичный регулятор (англ. Linear quadratic regulator, LQR) — в теории управления один из видов оптимальных регуляторов, использующий квадратичный функционал качества.

Задача, в которой система описывается линейными дифференциальными уравнениями, а показатель качества, представляет собой квадратичный функционал, называется задачей линейно-квадратичного управления.

Широкое распространение получили линейно-квадратичные регуляторы (LQR) и линейно-квадратичные гауссовы регуляторы (LQG).

Приступая к практическому решению задачи всегда нужно помнить об ограничениях

Для синтеза оптимального дискретного регулятора линейных стационарных систем нужна функция численного решения уравнения Беллмана.Такой функции в библиотеке Python Control Systems [1] нет, но можно воспользоваться функцией для решения уравнения Риккати, приведенной в публикации [2]:

Но нужно ещё учесть ограничения на синтез оптимального регулятора, приведенные в [3]:

• система, определяемая матрицами (A, B) должна быть стабилизируема;
• должны выполняться неравенства S> 0, Q – N/R–N.T>0, пара матриц (Q – N/R–N.T,
  A – B/R–B.T) не должна иметь наблюдаемые моды с собственными значениями на
  действительной оси.

После копаний в обширной и не однозначной теории, которую, по понятным причинам, я не привожу, задачу удалось решить, и все ответы можно прочитать прямо в комментариях к коду.

Структурная схема регулятора системы управления с обратной связью по всем переменным состояния изображена на рисунке:

Для каждого начального состояния x0 оптимальный линейный регулятор порождает оптимальное программное управление u*(x, k) и оптимальную траекторию х*(k).

Программа, формирующая модель оптимального управления с dlqr контролером

K=
[[ 0.82287566 -0.17712434]
[ 0.82287566 -0.17712434]]
P=
[[ 3.73431348 -1.41143783]
[-1.41143783 1.16143783]]
E=
[0.17712434+0.17712434j 0.17712434-0.17712434j]

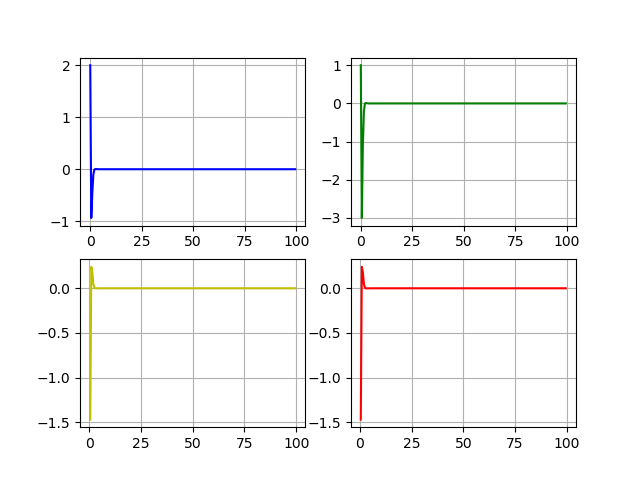
Динамика состояний и управлений: x1, x2, u1, u2.

Вывод

Отдельные задачи оптимального управления по типу приведенных можно решать средствами Python, комбинируя возможности библиотек Python Control Systems, SciPy,NumPy, что, безусловно, способствует популяризации Python, учитывая, что ранее такие задачи можно было решать только в платных математических пакетах.