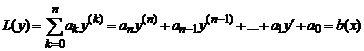Уравнения со специальной правой частью примеры

Уравнения с правой частью специального вида

Общее решение y_ОН линейного неоднородного дифференциального уравнения L(y)=b(x) есть сумма общего решения y_ОО соответствующего однородного уравнения L(y) = 0 и какого — либо частного решения y_ЧН исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто.

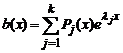
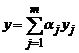
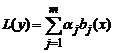
Функцию , где P_j(x) — некоторые полиномы (многочлены), назовём квазиполиномом. По теореме о наложении решений, если y_j , j=1,2. m — решения уравнений L(y) = b_j(x), то есть решение уравнения . Поэтому, не умаляя общности, будем считать, что правая часть уравнения L(y) = b(x) с постоянными коэффициентами имеет вид b(x) = P(x)e λx . В частности, если λ=α+βi — комплексное число, то наиболее общей правой частью указанного типа является функция

(1)

у которой P(x)и Q(x)- некоторые полиномы. Справедлив следующий результат.

Теорема. Линейное дифференциальное уравнение

с постоянными коэффициентами и правой частью вида (1) имеет частное решение

,

где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x) , S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x) , Q(x).

7.1. Уравнения с правой частью специального вида

Рассмотрим неоднородное линейное дифференциальное уравнение с постоянными коэффициентами

, (7.1)

Где , , …, , – вещественные числа.

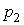
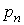
Уравнение (7.1) можно проинтегрировать рассмотренным ранее методом вариации произвольных постоянных, который сводится к составлению и решению системы линейных уравнений относительно функций, а также к интегрированию этих функций. Таких трудоемких операций можно избежать в некоторых случаях благодаря особому виду уравнения (7.1).

Поскольку общее решение соответствующего однородного уравнения (5.1) мы уже умеем находить, то получение общего решения уравнения (7.1) в силу теоремы подраздела 6.2 сводится к нахождению какого-нибудь частного его решения. Оказывается, что эта задача решается весьма просто при некоторых специальных видах функции 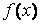в правой части уравнения (7.1). Далее рассматриваются следующие случаи.

1. Уравнения с правой частью в виде полинома.

В этом случае правая часть уравнения (7.1) представима в виде

,

Где – многочлен степени с известными коэффициентами.

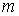
2. Правая часть в виде произведения полинома и экспоненты.

В данном случае правая часть уравнения (7.1) имеет вид

,

Где – многочлен степени с известными коэффициентами, – некоторое число.

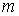
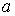
3. Правая часть в виде произведения полинома, экспоненты и гармонической функции.

В этом случае правая часть уравнения (7.1) имеет один из видов:

, ,

,

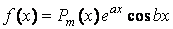
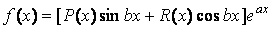
Где – многочлен степени с известными коэффициентами, и – многочлены известных степеней с известными коэффициентами, и – некоторые числа.

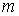
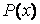
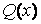
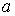
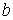
Для всех этих случаев на основании значений корней характеристического многочлена уравнения (7.1) и вида его правой части можно записать частное решение с точностью до коэффициентов входящих в него многочленов. Значения этих коэффициентов находятся путем составления и решения системы линейных алгебраических уравнений. Такой метод нахождения частного решения уравнения (7.1) называется Методом неопределенных коэффициентов.

Контрольная по математике. Примеры решения задач

Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Уравнения с правой частью специального вида.

Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.

Различают следующие случаи:

I. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

где — многочлен степени m.

Тогда частное решение ищется в виде:

Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.

Пример. Решить уравнение .

Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.

Частное решение ищем в виде: , где

Т.е.

Теперь определим неизвестные коэффициенты А и В.

Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

II. Правая часть линейного неоднородного дифференциального уравнения имеет вид:

Здесь Р1(х) и Р2(х) – многочлены степени m1 и m2 соответственно.

Тогда частное решение неоднородного уравнения будет иметь вид:

где число r показывает сколько раз число является корнем характеристического уравнения для соответствующего однородного уравнения, а Q1(x) и Q2(x) – многочлены степени не выше m, где m- большая из степеней m1 и m2.

Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.

Т.е. если уравнение имеет вид: , то частное решение этого уравнения будет где у1 и у2 – частные решения вспомогательных уравнений

и

Для иллюстрации решим пример другим способом.

Пример. Решить уравнение

Правую часть дифференциального уравнения представим в виде суммы двух функций f1(x) + f2(x) = x + (-sinx).

Составим и решим характеристическое уравнение:

Для функции f1(x) решение ищем в виде .

Получаем: Т.е.

Итого:

Для функции f2(x) решение ищем в виде: .

Анализируя функцию f2(x), получаем:

Таким образом,

Итого:

Т.е. искомое частное решение имеет вид: