4.2. Законы процессов переноса
Если газ выведен из состояния равновесия, то в нем возникают процессы, стремящиеся вернуть систему в равновесное состояние. Например, разные части системы имеют разные температуры или концентрации частиц. Соответственно, температуры или концентрации стремятся выровняться (за счет теплового движения молекул), что сопровождается передачей (переносом) тех или иных физических величин от одной части системы к другой. Такие процессы называются явлениями переноса. Эти явления имеют много общего и классифицируются по тому признаку, какая именно физическая характеристика «переносится» из одной части системы в другую.
Диффузия. Пусть в системе имеются молекулы, концентрация которых n(z) зависит от координаты z. Мысленно поместим в точке с координатой z квадратик площадью S, ортогональный оси z. В системе происходит процесс выравнивания концентрации n частиц, сопровождающийся их переносом в направлении убывания n. Эксперимент показал, что через площадь S за единицу времени проходит количество частиц
где D определяется свойствами системы и называется коэффициентом диффузии. Величина Ф (поток частиц — число частиц в единицу времени) имеет размерность
размерность концентрации частиц
и поэтому размерность коэффициента диффузии
Отрицательный знак в законе диффузии как раз и означает, что поток частиц направлен от больших значений концентрации к меньшим, то есть в направлении, противоположном производной dn/dz. Действительно, пусть n(z) — убывающая функция, то есть концентрация частиц падает с ростом z. Тогда производная dn/dz (градиент концентрации) отрицательна, а поток Ф получается положительным, то есть направлен в сторону увеличения z.
Если обе части уравнения (4.7) умножить на массу m0 диффундирующих молекул, то для потока массы М = m0Ф получим аналогичное уравнение
где r = т0n — масса диффундирующего вещества в единице объема, то есть его плотность. Связь (4.7) потока частиц с градиентом dn/dz концентрации называется первым законом Фика.
Первый закон Фика ничего не говорит о величине коэффициента диффузии, который должен в каждом конкретном случае определяться экспериментально. Поэтому этот закон носит эмпирический характер. Он применим не только для газов, но и для твердых и жидких тел. Следует отметить также, что перенос вещества в газах и жидкостях может осуществляться и механическим путем за счет конвекционных потоков (скажем, за счет ветра в атмосфере или течения в океане). Важно не путать диффузию, которая происходит из-за молекулярного движения, с конвекцией, возникающей вследствие воздействия внешних сил.
Заметим, что если система является смесью, то первый закон Фика записывается точно в такой же форме для каждого из компонентов смеси в отдельности, но коэффициенты диффузии, вообще говоря, различаются. Это значит, что в смеси, скажем, двух газов может случиться так, что концентрация частиц одного из компонентов уже выровнялась, а второго — еще нет.
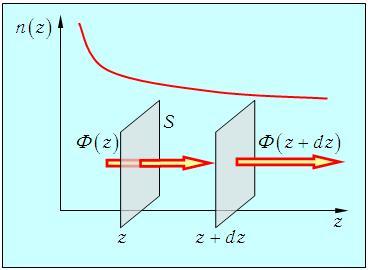
Второй закон Фика позволяет найти зависимость концентрации диффундирующих частиц от времени. Для его вывода рассмотрим два параллельных друг другу одинаковых квадратика, расположенных в близких точках с координатами z и z + dz. Для определенности будем считать, что n(z) — убывающая функция (рис. 4.4).
Рис. 4.4. Иллюстрация явления диффузии (к выводу второго закона Фика)
Тогда через левую площадку за время dt входит Ф(z)dt частиц, а через правую выходит Ф(z + dz)dt частиц.
Увеличение числа частиц dN в пространстве между площадками за время dt равно разности числа входящих и выходящих частиц:
Разделив dN на объем Sdz зазора между квадратиками, получаем изменение концентрации частиц за время dt
Используя первый закон Фика, находим отсюда (здесь мы уже переходим к частным производным)
Обычно коэффициент диффузии не зависит от координат, и мы получаем уравнение, выражающее второй закон Фика:
Если ввести плотность потока частиц j = Ф/S (число частиц, пересекающих единичную площадь в единицу времени), то уравнение (4.8) можно записать в иной форме:
Это уравнение — один из примеров уравнения непрерывности, встречающегося во многих областях физики и выражающего в данном случае закон сохранения числа частиц. Его смысл: скорость изменения числа частиц в объеме равна разности потоков входящих и выходящих частиц (при условии, что внутри объема не происходит рождения или исчезновения частиц).
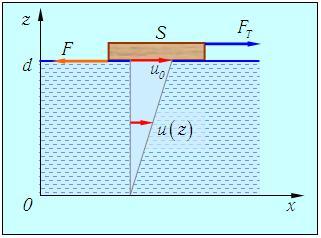
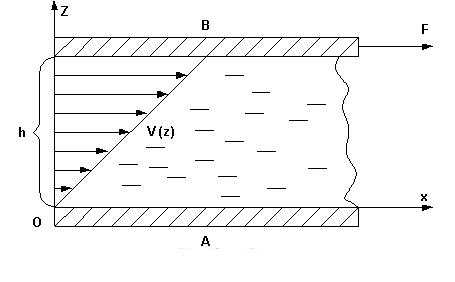
Вязкость. Рассмотрим следующий мысленный опыт. Пусть на поверхности жидкости плавает пластина, которую медленно тянут направо с силой FT (рис. 4.3).
Рис. 4.5. Сила внутреннего трения F, действующая на пластину, движущуюся со скоростью u0, по поверхности жидкости
Опыт показывает, что при установившемся движении пластина перемещается с постоянной скоростью u0. Пусть расстояние до неподвижного дна равно d, а площадь пластины равна S. Что мы можем сказать о течении жидкости?
Ясно, что кроме силы FT на пластину должно действовать что-то еще: иначе она двигалась бы равноускоренно. Это «что-то еще» может действовать только со стороны жидкости. Другими словами, на пластину со стороны жидкости действует сила F, подобная силе трения. Она направлена влево и по величине равна действующей силе FT. Каково происхождение этой силы? Прилегающий к пластине слой жидкости «прилипает» к ней и движется с той же скоростью u0. Аналогично слой жидкости, прилегающий ко дну, имеет нулевую скорость. Следовательно, в системе устанавливается некоторое распределение скоростей u(z), где z — расстояние от дна. В конечном итоге неподвижное дно через жидкость действует на пластину, порождая силу внутреннего трения, уже знакомую нам из механики жидкостей и газов.
В соответствии со сказанным, заведомо должны выполняться граничные условия u(0) = 0, u(d) = u0. Сила внутреннего трения возникает как раз вследствие этого распределения скоростей: вышележащий слой «трется» о нижележащий и тормозится им (соответственно, более быстрый слой стремится ускорить более медленный).
Опыт показывает, что сила внутреннего трения F связана со скоростью u0 соотношением (см. рис. 4.3)
Коэффициент h, имеющий размерность
называется коэффициентом динамической вязкости (внутреннего трения).
Чтобы найти распределение скоростей в этой системе, представим себе наблюдателя, находящегося на расстоянии z от дна и движущегося вместе с жидкостью со скоростью u(z). С точки зрения этого наблюдателя, его слой покоится, а пластина движется со скоростью u0 – u(z). Зависимость той же силы F от скорости должна теперь описываться аналогичной формулой с заменой
В результате получаем
Приравнивая выражения (4.11) и (4.12), находим скорость слоя как функцию расстояния от дна
Мы получили линейный закон распределения скоростей (рис. 4.6), удовлетворяющий нашим граничным условиям u(0) = 0, u(d) = u0.
Рис. 4.6 Линейное распределение скоростей в жидкости
Такое распределение скоростей связано с простотой рассмотренной системы. В других случаях течение имеет более сложный характер, но и тогда мы можем воспользоваться найденной закономерностью. Действительно, рассмотрим жидкость, в которой существует градиент скоростей по координате z. Относительная скорость слоев с координатами z и z + dz равна
Поскольку мы рассматриваем сколь угодно малые расстояния dz, то для малых площадей S течение можно считать плоским и описываемым прежними формулами. Тогда сила внутреннего трения между соседними слоями будет определяться уравнением (4.11), где вместо отношения u0/d стоит градиент скорости относительного движения слоев du/dz:
Такой закон действительно соответствует опытам по определению силы внутреннего трения между слоями жидкости или газа при ламинарном течении и был установлен Ньютоном.
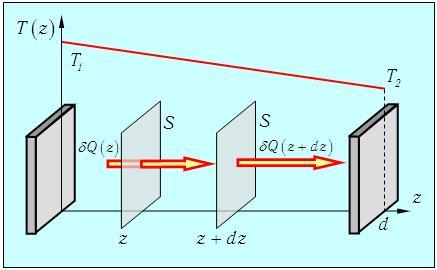
Теплопроводность. Предположим теперь, что есть два источника тепла различной температуры Т1 и Т2. Представим их себе как широкие пластины, расположенные перпендикулярно оси z в точках с координатами z = 0 и z = d. Газ, заполняющий зазор между пластинами, передает тепловую энергию от горячего тела к более холодному. При этом в газе устанавливается некоторое распределение температур T(z), удовлетворяющее граничным условиям Т(0) = T1 и T(d) = Т2 (рис. 4.).
Рис. 4.7. Распределение температуры между двумя источниками
Поместим между источниками квадратик площадью S, параллельный пластинам. Опыт показывает, что за время dt через площадь S протекает количество теплоты dQ, причем
Постоянная k называется коэффициентом теплопроводности и имеет размерность
Соотношение (4.15) называется законом Фурье.
Отрицательный знак (как и в первом законе Фика) указывает, что поток тепла направлен в сторону понижения температуры, то есть против градиента температуры dT/dz. При этих условиях в равновесном состоянии в газе установится линейный закон изменения температуры. Действительно, через квадратик единичной площади, расположенный в точке z, в единицу времени втекает количество теплоты
Через такой же квадратик в точке z + dz в единицу времени вытекает теплота
Если температура между квадратиками не меняется (установилось равновесие), то эти потоки теплоты равны между собой, то есть
Из равенства нулю второй производной следует, что функция линейна:
Из граничных условий в концевых точках находим константы интегрирования:
В сущности, мы получили аналог закона распределения скоростей при рассмотрении вязкости жидкости: достаточно заменить
Это следствие стационарности, то есть того факта, что мы рассматривали установившееся течение или распределение температур. То же следует из второго закона Фика: для стационарной системы: производная по времени в левой части уравнения (4.9) равна нулю, откуда следует равенство нулю второй производной концентрации частиц по координате z, что эквивалентно линейности функции n(z).
Пример. Определим, какое количество тепловой энергии уносится в единицу времени через окно площадью S = 2 м 2 с расстоянием между стеклами d = 5 см, если в комнате поддерживается температура t1 = 20 °С, а на улице стоит мороз:
t2 = –20 °С.
Сразу заметим, что поскольку величина градуса по шкалам Цельсия и Кельвина одинакова, то разность температур
Коэффициент теплопроводности воздуха k = 0,025 Дж/(м·с·К). Для стекла этот коэффициент в 20 раз больше, так что его наличие можно не учитывать. К тому же толщина стекла много меньше промежутка между стеклами. Поэтому от мороза нас оберегает именно воздушная прослойка между стеклами. В соответствии со сказанным, в этом промежутке устанавливается линейное распределение температуры, так что производная dT/dz постоянна и равна
Поток тепловой энергии равен тогда
Расход тепловой энергии через одно окно за месяц
Решая эту задачу, мы неявно сделали сильное предположение, что температура внутреннего стекла совпадает с температурой в комнате, а наружного — с температурой окружающего воздуха. Из практики каждый знает, что это не так: на самом деле наружная поверхность стекла несколько теплее, а внутренняя — немного холоднее. В действительности градиент температур в промежутке между рамами может быть раза в два меньше, что соответственно уменьшает поток тепловой энергии наружу. Однако точное решение задачи выходит за рамки данного курса.
Нетрудно заметить то общее, что есть у всех обсуждавшихся явлений. Во все уравнения переноса входит градиент некоторой величины — концентрации частиц, скорости течения, температуры. Во всех случаях при условии стационарности устанавливается линейное распределение этой величины. Все это потому, что явления переноса имеют общее происхождение — молекулярное движение.
Явление переноса. Общее уравнение переноса
1.3 Явление переноса. Общее уравнение переноса
Группа явлений, обусловленных хаотическим движением молекул и приводящих при этом к передаче массы, кинетической энергии и импульса, называется явлением переноса.
К ним относят диффузию – перенос вещества, теплопроводимость – перенос кинетической энергии и внутреннее трение – перенос импульса.
Общее уравнение переноса, описывающее эти явления, можно получить на основе молекулярно-кинетической теории.
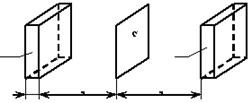
Пусть через площадку площадью «S» (рисунок) переносится некоторая физическая величина в результате хаотического движения молекул.
Похожие работы
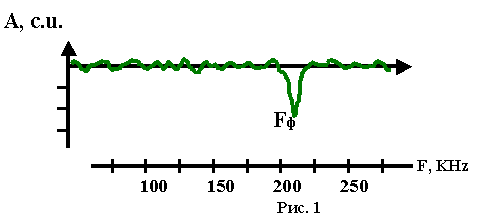
. материалы хорошо описываются в рамках квантово-механической фононной Модели строения и функционирования клеточных мембран, что позволяет утверждать: “ФОНОН – КВАНТ биологической (клеточной) мембраны”. Модель пригодна для объяснения широкого круга наблюдаемых явлений. При этом наблюдаемые явления описываются в рамках единого понятийного аппарата и не требуют специфических допущений для описания .
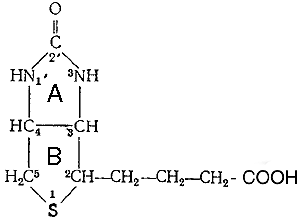
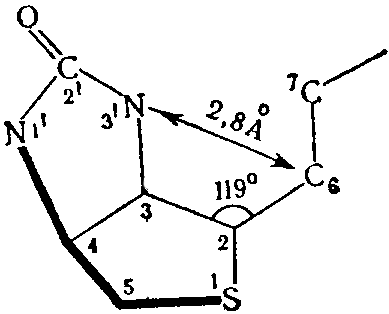
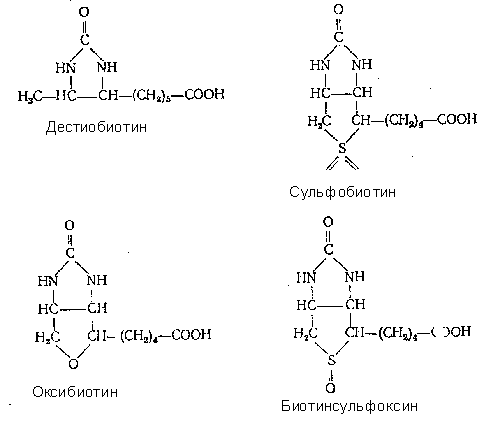
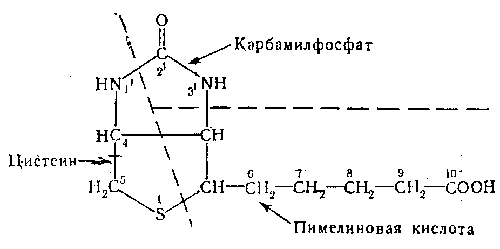
. активность тиамина и некоторых его производных. За последние 20 лет наряду выяснением механизма основных реакций, в которых каталитическую роль играет ТДФ, стали накапливаться данные о высокой биологической активности других некоферментных производных тиамина. Отчетливо наметились два направления исследований: возможное, участие различных фосфорных эфиров витамина в активном переносе .
. формами географической (территориально-механической) изоляции, известны и разные формы биологической изоляции, которые могут быть разбиты на три основные группы: эколого-этологическую, морфо-физиологическую и собственно генетическую. Биологическая изоляция приводит к уменьшению вероятности встречи особей разных полов в период размножения, снижению полового влечения и эффективности спаривания, к .
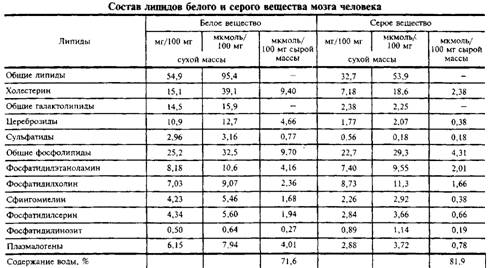
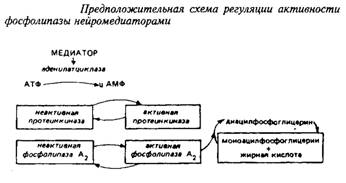
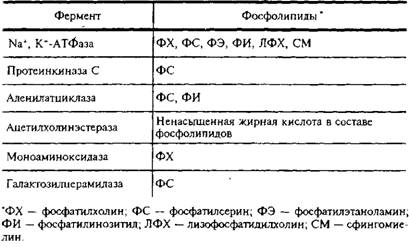
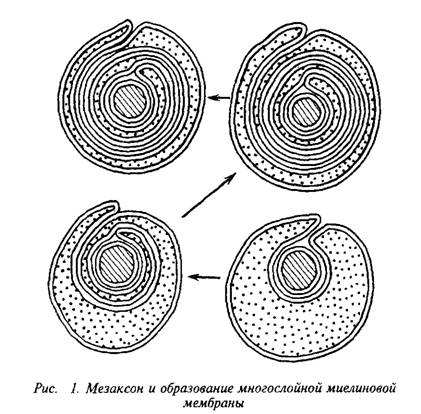
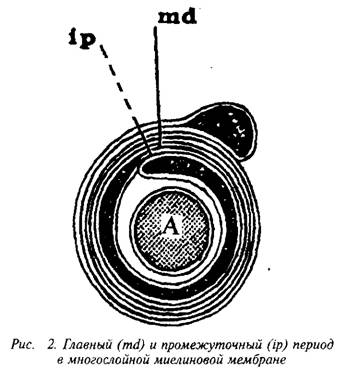
. и инозитолтрифосфат подвергаются химическим превращениям, требующим АТФ и ЦТФ и приводящим к восстановлению три-фосфоинозитида. Таким образом, цикл замыкается и уровень полифосфоинозитидов в мембране восстанавливается. 7. МИЕЛИН В ЦЕНТРАЛЬНОЙ НЕРВНОЙ СИСТЕМЕ Мозг человека содержит 120 г миелина, что составляет одну треть его сухой массы. Миелин – уникальное образование, организация которого .
Общее уравнение явлений переноса. Явления переноса. Общее уравнение явлений переноса в газах.
Читайте также:
|

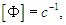
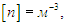
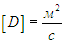
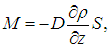
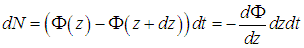
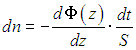
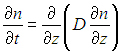
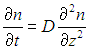
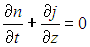
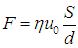
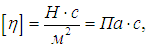

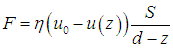
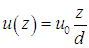
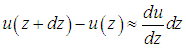
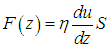
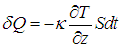
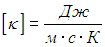
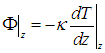
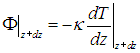

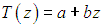
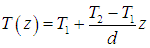
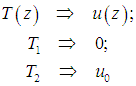
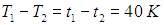

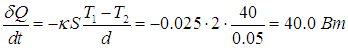
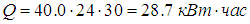
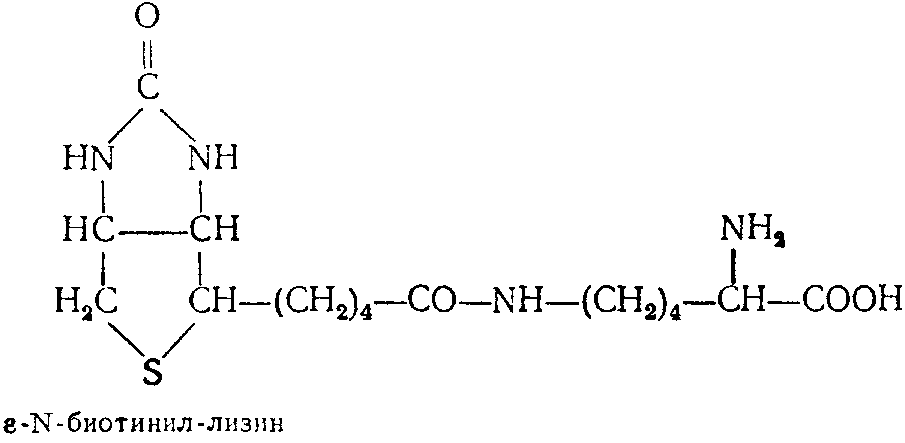
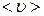 .
.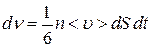 , (4.4.1)
, (4.4.1)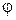 , отнесенная к одной молекуле, изменяется только в направлении оси X. Значение этой величины изменяется при столкновениях молекул и сохраняется постоянной между соударениями, т. е. на длине свободного пробега
, отнесенная к одной молекуле, изменяется только в направлении оси X. Значение этой величины изменяется при столкновениях молекул и сохраняется постоянной между соударениями, т. е. на длине свободного пробега 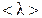 . Расположим площадку dS, перпендикулярно оси X, в точке x (рис. 60).
. Расположим площадку dS, перпендикулярно оси X, в точке x (рис. 60).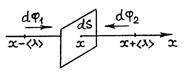
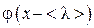 . Поток этой величины, согласно (4.4.1)
. Поток этой величины, согласно (4.4.1)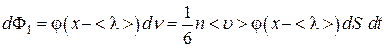 . (4.4.2)
. (4.4.2)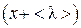 справа налево
справа налево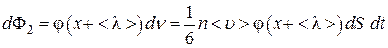 . (4.4.3)
. (4.4.3)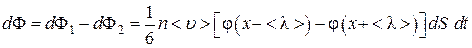 . (4.4.4)
. (4.4.4)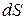 слева направо и справа налево были бы одинаковы, и результирующий поток был бы равен нулю. Поэтому, чтобы выявить сущность явлений переноса, берется разность соответствующих потоков, которая определяет поток
слева направо и справа налево были бы одинаковы, и результирующий поток был бы равен нулю. Поэтому, чтобы выявить сущность явлений переноса, берется разность соответствующих потоков, которая определяет поток 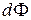 в направлении оси X.
в направлении оси X.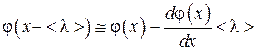 , (4.4.5)
, (4.4.5)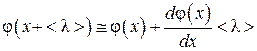 . (4.4.6)
. (4.4.6)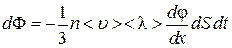 . (4.4.7)
. (4.4.7)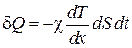 , (4.5.1)
, (4.5.1)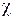 – коэффициент теплопроводности, который, как видно из закона Ж. Фурье, имеет в системе СИ размерность Дж/(м∙с∙K) = Вт/(м∙K), и численно равен количеству тепла, переносимого в единицу времени через единичную площадку при градиенте температуры, равном единице. Знак “минус” означает, что тепло переносится от мест более горячих к более холодным.
– коэффициент теплопроводности, который, как видно из закона Ж. Фурье, имеет в системе СИ размерность Дж/(м∙с∙K) = Вт/(м∙K), и численно равен количеству тепла, переносимого в единицу времени через единичную площадку при градиенте температуры, равном единице. Знак “минус” означает, что тепло переносится от мест более горячих к более холодным.
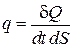 , (4.5.2)
, (4.5.2)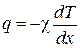 . (4.5.3)
. (4.5.3)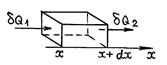
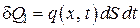 , (4.5.4)
, (4.5.4)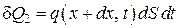 . (4.5.5)
. (4.5.5) . (4.5.6)
. (4.5.6) , (4.5.7)
, (4.5.7)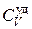 и
и  – удельная теплоемкость и плотность вещества.
– удельная теплоемкость и плотность вещества.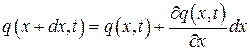 . (4.5.8)
. (4.5.8)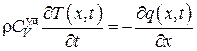 . (4.5.9)
. (4.5.9) . (4.5.10)
. (4.5.10)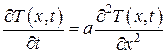 . (4.5.11)
. (4.5.11)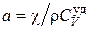 – коэффициент температуропроводности.
– коэффициент температуропроводности.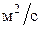 . В нестационарных тепловых процессах коэффициент a характеризует скорость изменения температуры. Если коэффициент теплопроводности
. В нестационарных тепловых процессах коэффициент a характеризует скорость изменения температуры. Если коэффициент теплопроводности 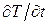 для любой точки вещества пропорционально величине a. Поэтому при прочих одинаковых условиях быстрее увеличивается температура у того вещества, которое имеет больший коэффициент температуропроводности. Сама же величина a тем больше, чем больше тепла способно пропустить вещество в единицу времени через единичную площадку при единичном градиенте температуры (т. е. чем больше
для любой точки вещества пропорционально величине a. Поэтому при прочих одинаковых условиях быстрее увеличивается температура у того вещества, которое имеет больший коэффициент температуропроводности. Сама же величина a тем больше, чем больше тепла способно пропустить вещество в единицу времени через единичную площадку при единичном градиенте температуры (т. е. чем больше