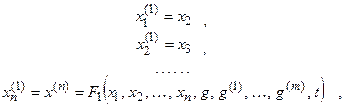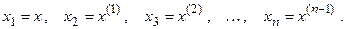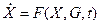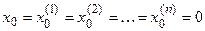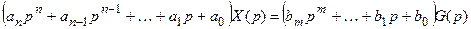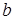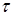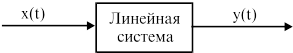УРАВНЕНИЯ ДИНАМИКИ И СТАТИКИ
Динамика рассматривает состояние движения, ход развития процессов во времени. Динамика процессов обычно описывается дифференциальными или разностными уравнениями.
Будем рассматривать систему
 |
Поведение исследуемой системы описывается дифференциальными уравнениями. Так зависимость выходного сигнала 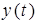
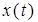
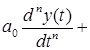
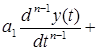
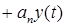
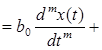
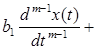
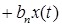
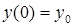
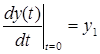
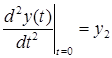
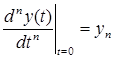
— начальные условия. Уравнение 2.1. является уравнением динамики рассматриваемой системы.
Пусть поведение системы Рис.2.1 описывается уравнением
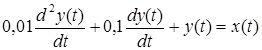
Будем предполагать, что 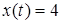
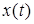
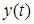
В отличии от динамики, рассматривающей процессы протекающие в системе
во времени, статика изучает состояние покоя или равновесия. В этом случае
отсутствует временной фактор.
Из уравнения динамики (2.1), приравняв нулю все производные (так как режим установившейся), нетрудно получить уравнение статики системы
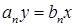
где 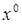
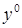
Из уравнения статики можно получить статическую характеристику системы, представляющую собой зависимость выходной величины от входной в статическом режиме
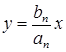
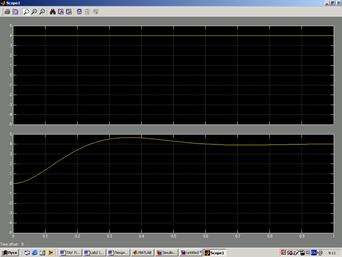
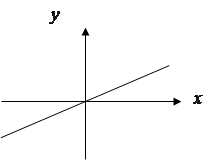
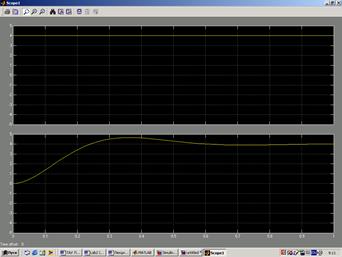
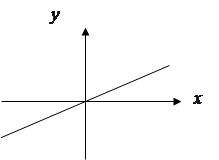
Представим статическую характеристику в виде графика Рис.2.3.
Статическая характеристика может быть получена экспериментально путем подачи на вход системы постоянных воздействий и измерения установившихся значений выходных величин.
Дата добавления: 2019-12-09 ; просмотров: 400 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Уравнения динамики и статики
При проектировании и исследовании САУ необходимо знать уравнения, описывающие их движения. Процессы в САУ описываются дифференциальными, разностными, интегральными и интегро-дифференциальными уравнениями, которые называют ее математической моделью. При исследовании САУ на различных этапах математическая модель может быть различной. Начинают исследования САУ с простейшей математической моделью, а затем ее усложняют, учитывая дополнительные связи и влияния. Такой подход объясняется тем, что к математической модели предъявляются противоречивые требования. Математическая модель должна достаточно полно описывать динамику САУ и при этом быть по возможности простой.
В дальнейшем будут рассматриваться только обыкновенные дифференциальные уравнения, в неявной форме которые могут быть записаны
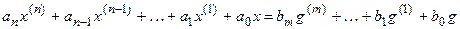
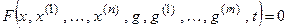
| x, x ( i ) | — управляемая (выходная) величина и ее производные 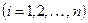 ; ; |
| g, g ( j ) | — задающая (входная) величина и ее производные 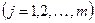 ; ; |
| ai и bj | — постоянные коэффициенты, зависящие от параметров системы; |
| с и m | — числа, определяющие порядок производных 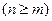 , причем n определяет порядок дифференциального уравнения; , причем n определяет порядок дифференциального уравнения; |
| t | — независимая переменная (время). |
Уравнения (3.1) и (3.2) могут быть записаны в явной форме, разрешенные относительно старшей производной (например, (3.2))
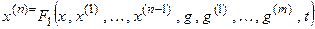
Данное дифференциальное уравнение в явной форме n-го порядка можно преобразовать в систему n дифференциальных уравнений первого порядка:
путем введения новых неизвестных
Если в дифференциальное уравнение (3.2) входит n неизвестных функций 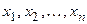
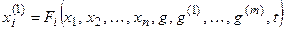
где 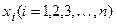
В векторной форме дифференциальное уравнение будет иметь вид


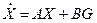
| где | X – вектор выходных величин (параметров состояний); |
| G – вектор задающих (входных) величин; | |
| A – матрица объекта управления с элементами aij; | |
| B – матрица задающих величин с элементами bij . |
Широкое применение в ТАУ получила операторная форма записи дифференциального уравнения. Это объясняется тем, что от дифференциального уравнения посредством интегрального преобразования (например, преобразования Лапласа) переходят к операторной форме. Операторное уравнение является алгебраическим и его решение проще, чем дифференциальное. Затем из полученного решения операторного уравнения с помощью обратного преобразования получают решение дифференциального уравнения.
Дифференциальное уравнение (3.1) при нулевых начальных условиях
в операторной форме можно записать
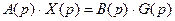
где 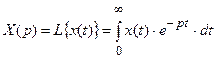
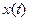
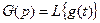
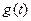
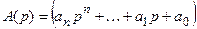
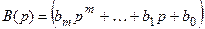
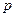
Операторная форма записи дифференциального уравнения, когда начальные условия по всем переменным равны нулю, совпадает с символической формой, когда 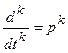
Уравнение движения САУ в любой форме полностью описывает весь процесс управления, т.е. процесс изменения управляемых величин как в переходном, так и в установившемся режимах.
Под установившимся режимом понимают процесс, при котором регулируемая (управляемая) величина изменяется по закону, определяемому лишь законом изменения задающего воздействия. Установившейся режим САУ, относительно которого рассматривается движение системы в процессе управления, называется исходным.
Переходным режимом называется изменение управляемой величины при переходе САУ из одного в другое установившееся состояние.
Если в установившемся режиме воздействия после их приложения больше не изменяют своих величин во времени, то в САУ устанавливается так называемый статический режим.
Уравнение статики может быть получено из уравнения движения САУ (3.1), если все члены, содержащие производные, приравнять нулю, то есть
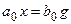
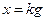
где 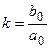
Графическое отображение данной зависимости, т.е. зависимости между выходной x и входной g величинами САУ в статическом режиме, называется статической характеристикой (рис. 3.1).
 |
Рис.3.1. Статические характеристики элементов САУ
Статические характеристики элементов САУ и систем в целом могут быть как линейными (кривая 1, рис. 3.1), так и нелинейными (кривая 2, рис. 3.1). Если характеристика нелинейная, то необходимо учитывать влияние данной нелинейности на динамику САУ.
Дата добавления: 2015-12-11 ; просмотров: 1349 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
УРАВНЕНИЯ ДИНАМИКИ И СТАТИКИ
Динамика рассматривает состояние движения, ход развития процессов во времени. Динамика процессов обычно описывается дифференциальными или разностными уравнениями.
Будем рассматривать систему
 |
Поведение исследуемой системы описывается дифференциальными уравнениями. Так зависимость выходного сигнала 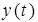
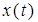
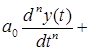
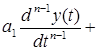
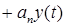
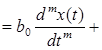
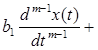
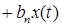
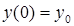
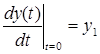
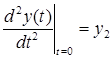
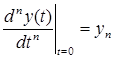
— начальные условия. Уравнение 2.1. является уравнением динамики рассматриваемой системы.
Пусть поведение системы Рис.2.1 описывается уравнением
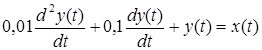
Будем предполагать, что 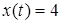
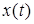
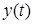
В отличии от динамики, рассматривающей процессы протекающие в системе
во времени, статика изучает состояние покоя или равновесия. В этом случае
отсутствует временной фактор.
Из уравнения динамики (2.1), приравняв нулю все производные (так как режим установившейся), нетрудно получить уравнение статики системы

где 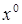
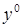
Из уравнения статики можно получить статическую характеристику системы, представляющую собой зависимость выходной величины от входной в статическом режиме
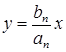
Представим статическую характеристику в виде графика Рис.2.3.
Статическая характеристика может быть получена экспериментально путем подачи на вход системы постоянных воздействий и измерения установившихся значений выходных величин.
2.2. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ
|
Пусть система
описывается следующим дифференциальным уравнением
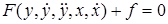
где 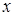
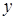
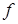
Уравнение (2.3) является нелинейным. Процесс исследования нелинейных систем существенно сложнее процесса исследования линейных. Поэтому исследование нелинейных систем стремятся свести к исследованию линейных. Процедура преобразования нелинейных уравнений в линейные называется линеаризацией.
Процедура линеаризации базируется на разложении нелинейных функций, входящих в уравнения, в ряд Тейлора. Необходимо отметить, что разложение какой либо функции в ряд Тейлора происходит в достаточно малых окрестностях некоторой точки. В качестве такой точки берется точка, соответствующая заданному режиму работы системы. В установившемся состоянии это может быть режим равновесия. Заметим, что отклонения реальных значений входных и выходных сигналов от их заданных значений в нормально работающей замкнутой автоматической системе не велико. Система работает по принципу парирования таких отклонений.
Обозначим переменные, соответствующие заданному режиму работы системы
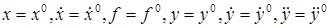
Введем отклонения реальных значений сигналов от требуемых
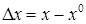
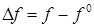
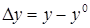
Тогда
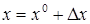
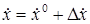
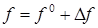
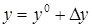
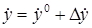
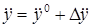
Рассматривая функцию 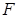
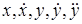
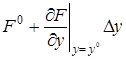
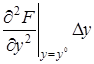
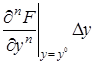
+ 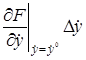
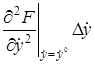
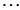
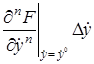
+ 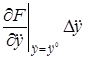
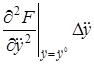
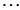
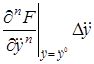
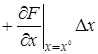
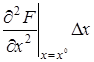
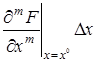
+ 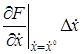
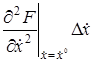
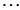
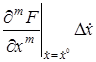
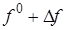
В этом выражении оставим только первые члены разложения, отбросив малые члены более высокого порядка.
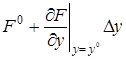
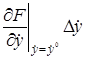
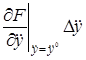
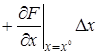
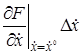
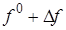
В заданном режиме уравнение (2.3) примет вид
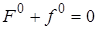
Вычтем это уравнение из (2.5), получим
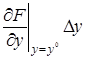
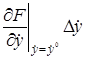
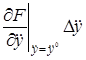
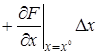
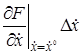
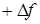
Введем обозначения
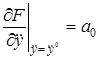
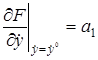
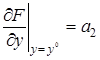
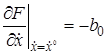
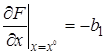
Подставив их в (2.6) и отбросив знак 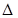
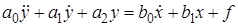
Линеаризация уравнения (2.3) была проведена в предположениях:
— отклонения входных 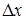
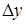
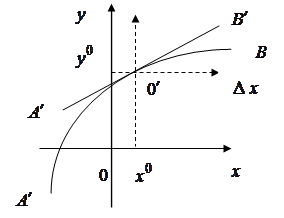
— функция 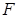
— линеаризованное уравнение (2.7) является уравнением в отклонениях.
|
Рассмотрим Рис.2.5.
 |
В этом случае нелинейная зависимость между 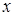
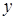
кривой 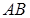
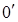
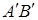
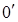
2.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО ОСНОВНЫЕ
СВОЙСТВА
Преобразованием Лапласа называется следующее соотношение
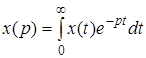
где 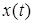
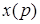
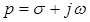
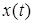
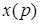
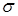
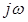
Функцию 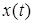
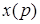
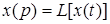
где 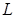
Функция 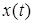
— должна быть определена и кусочно-дифференцируема на всей положительной числовой полуоси 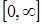
— 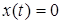
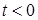
— существуют такие положительные числа 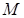
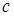
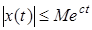
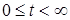
С помощью обратного преобразования Лапласа
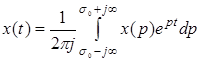
можно найти по известному изображению его оригинал. В нем интеграл берется вдоль любой прямой 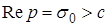
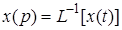
где 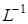
Рассмотрим основные свойства преобразования Лапласа.
1. Свойство линейности. Для любых постоянных 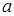
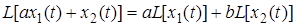
2. Дифференцирование оригинала.
Для первой производной
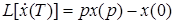
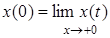
Для n-й производной
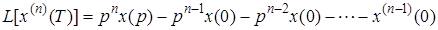
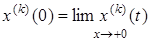
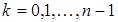
Если начальные условия нулевые
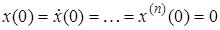
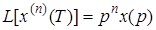
Таким образом, n-кратное дифференцирование оригинала при нулевых начальных условиях, соответствует умножению изображению на n-ю степень 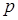
3. Интегрирование оригинала сводится к делению изображения на 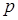
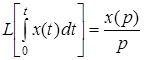
4. Теорема запаздывания. Для любого положительного
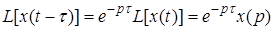
5. Теорема о свертке. Если 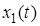
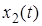
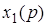
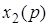
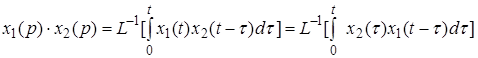
Интеграл правой части называется сверткой функций 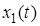
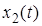
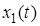
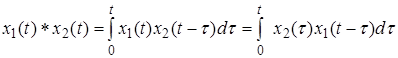
6. Теорема о предельных значениях. Если 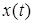
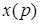
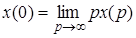
и при существовании предела 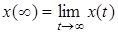
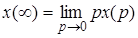
2.4. Запись дифференциальных уравнений в символическом виде.
Будем рассматривать следующую систему
Пусть в общем случае линейная система описывается дифференциальным уравнением n-го порядка
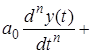
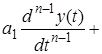
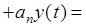
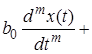
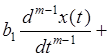
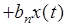
где 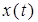
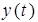
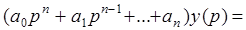
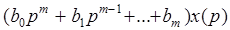
где 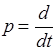
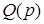
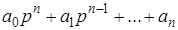
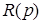
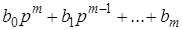
Тогда уравнение (2.11) можно записать в более компактно
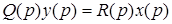
2.5. C тандартная форма записи линейных дифференциальных
уравнений
Принято, что линейные дифференциальные уравнения не выше второго порядка записываются в стандартной форме, а именно:
— члены уравнения, содержащие выходную величину и ее производные, записываются в левой части уравнения;
— все остальные члены уравнения, записываются справа;
— коэффициент при выходной величине делают равным единице;
— коэффициенты при входных и выходных величинах и их производных являются либо постоянными времени, либо коэффициентами передачи (усиления).
Рассмотрим дифференциальное уравнение в символическом виде
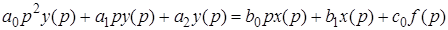
Разделим обе части этого уравнения на 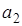
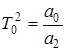
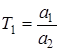
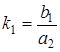
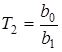
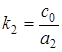
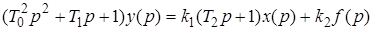
Здесь 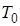
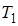
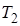
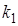
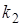
2.5. Передаточные функции.
Передаточной функцией системы называется отношение выходного сигнала к входному, преобразованных по Лапласу при нулевых начальных условиях. Тогда передаточная функция рассматриваемой системы (Рис.2.6) равна
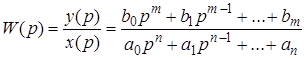
 |
Пусть ее поведение описывается следующим дифференциальным уравнением в символической записи
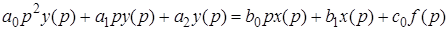
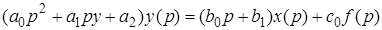
Приведем это уравнение к виду
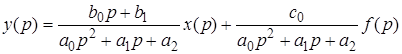
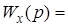
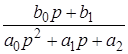
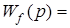
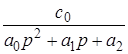
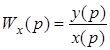
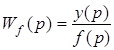
Если линейная система имеет несколько входов, то при определении передаточной функции по одному из входов, другие входы полагаются равными нулю.
http://helpiks.org/6-18020.html
http://megaobuchalka.ru/15/10022.html