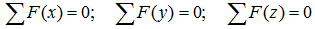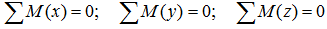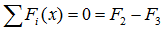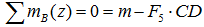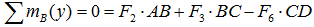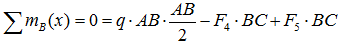Уравнения статики в теоретической механике

Статика – раздел теоретической механики

Определение и роль статики в теоретической механике

Основной задачей статики является установление законов преобразования системы сил в эквивалентные системы. Методы статики применяются не только при изучении тел, находящихся в равновесии, но и в динамике твердого тела, при преобразовании сил в более простые эквивалентные системы.

Под состоянием равновесия, в статике, понимается состояние, при котором все части механической системы покоятся относительно некоторой инерциальной системы координат. Одним из базовых объектов статики являются силы и точки их приложения.

Понятие силы

Единицей измерения силы является один Ньютон:
.
В технике широко используется килоньютон:
.

Как следует из определения, сила – это векторная величина, которая, в трехмерном пространстве, имеет три проекции на оси координат. Также задать силу можно с помощью абсолютной величины (модуля) и направления. Для материальной точки, сила приложена к самой точке. Но если мы рассматриваем твердое тело, то кроме вектора силы нам нужно еще указать и точку ее приложения. Таким образом, действие силы на твердое тело характеризуется вектором силы и точкой ее приложения. Если выбрать систему отсчета, то действие силы на твердое тело определяется двумя векторами. Это вектор силы, и вектор, проведенный из начала системы отсчета в точку приложения силы.

Система сил, действующих на тело – это совокупность векторов сил, приложенных к телу, и точек их приложения.
Эквивалентные системы сил Две системы сил являются эквивалентными, если законы движения любых точек твердого тела совпадают при действии любой из этих систем.
Эквивалентное преобразование системы сил – это переход от одной системы сил к эквивалентной ей системе.
Система взаимно уравновешивающихся сил – это система сил, не меняющая уравнений движения или уравнений равновесия твердого тела. То есть это система, эквивалентная отсутствию сил.
Равнодействующая – это одна сила, действие которой эквивалентно действию данной системы сил.

Закрепленные, скользящие и свободные векторы

Поскольку действие силы на твердое тело определяется двумя векторами, то часто под силой подразумевают множество, состоящее из двух векторов – вектора силы, и вектора точки ее приложения относительно выбранной системы координат. Такие множества подразделяются на три класса, для которых вводят специальные термины.

Закрепленный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два закрепленных вектора считаются равными только в том случае, если равны их образующие векторы и совпадают точки приложения. Закрепленный вектор также называют связанным или фиксированным вектором.
Скользящий вектор – это множество, состоящее из образующего вектора и точки его приложения, обладающее тем свойством, что точку приложения можно перемещать вдоль прямой, параллельно образующему вектору. То есть два скользящих вектора считаются равными, если равны образующие векторы и точки их приложения расположены на одной прямой, параллельной образующему вектору.
Свободный вектор – это множество, состоящее из образующего вектора и точки его приложения. Два свободных вектора считаются равными, если равны образующие векторы, не зависимо от точек приложения.
Линия действия силы – это прямая, проведенная через точку приложения силы параллельно ее направлению.

Если мы рассматриваем упругое тело, то сила – это закрепленный вектор. Деформации зависят не только от величин и направлений сил, но и от точек их приложения. Если мы рассматриваем движение или равновесие абсолютно твердого тела, то действующая сила является скользящим вектором. Перемещение ее точки приложения вдоль линии ее действия не меняет уравнений движения или уравнений равновесия. Угловая скорость вращения абсолютно твердого тела является свободным вектором. Она характеризует движение в целом, и ее значение одинаково во всех точках тела.

С математической точки зрения, статика – это алгебра скользящих векторов.

Проекции силы на оси координат

Сила в трехмерном пространстве

Пусть у нас есть декартова система координат Oxyz . И пусть – единичные векторы, направленные вдоль ее осей , и , соответственно. Пусть – проекции вектора силы на оси координат. Тогда разложение силы на составляющие вдоль координатных осей имеет вид:
.
Абсолютное значение (модуль) силы:
.

Введем единичный вектор , направленный вдоль вектора силы . Тогда
.
Эта формула выражает тот факт, что вектор силы можно задать, указав ее модуль F и направление . Вектор имеет три проекции на оси координат: . Поскольку его длина равна единице: , то они связаны соотношением:
.
То есть единичный вектор имеет только две независимые компоненты. Таким образом, для задания вектора силы нужно знать три величины:
либо три проекции на оси координат ;
либо модуль F и направление , которое задается двумя независимыми величинами.

Введем углы между вектором силы и осями координат , и . Тогда проекции силы на оси координат определяются по формулам:
;
.
Косинусы углов называются направляющими косинусами.

Направляющие косинусы вектора – это косинусы углов между вектором и осями координат. Они являются проекциями единичного вектора , сонаправленного с :
,
и связаны соотношением:
.

Сила на плоскости

Результаты, приведенные выше, можно применить и для плоской декартовой системы координат Oxy . В этом случае имеем:
;
;
;
;
;
;
.
Поскольку , то . Последнее уравнение представляет собой известную тригонометрическую формулу:
.
Для задания вектора силы , необходимо знать две независимые величины:
либо проекции вектора на оси координат ;
либо модуль F и направление , которое задается одним углом .

Аксиомы статики

Часть аксиом являются основными законами механики. Другая часть относится к законам преобразования сил, действующих на абсолютно твердое тело, и применяется только к задачам теоретической механики. По своей сути, они выражают собой тот факт, что действие силы на тело является скользящим вектором.

1. Аксиома инерции (закон инерции Галилея)
Существуют такие системы отсчета, в которых любая материальная точка, не взаимодействующая с другими телами и точками, движется прямолинейно и равномерно. В частности, если тело покоилось в определенный момент времени, то оно будет покоиться и в последующие моменты.

Такие системы отсчета называются инерциальными. В механике, если это особо не оговорено, под системой отсчета подразумевается именно инерциальная система отсчета. Аксиому инерции иногда формулируют так.

1′. Аксиома инерции
В инерциальной системе отсчета, под действием взаимно уравновешивающихся сил, материальная точка находится в состоянии покоя или движется прямолинейно и равномерно, а первоначально покоившееся тело продолжает покоиться и в последующие моменты времени.

2. Аксиома равновесия двух сил
Две силы, приложенные к абсолютно твердому телу, являются уравновешенными тогда и только тогда, когда они равны по модулю, направлены в противоположные стороны и их линии действия совпадают.

3. Аксиома присоединения и исключения уравновешивающихся сил
Кинематическое состояние твердого тела не изменится, если к действующей на него системе сил прибавить или отнять уравновешенную систему сил.

То есть, прибавляя или исключая уравновешенную систему сил, мы получаем эквивалентную систему сил.

Следствие аксиом 2 и 3
Действие силы на твердое тело не изменится, если точку приложения силы перенести вдоль ее линии действия. То есть сила, приложенная к твердому телу, является скользящим вектором. Доказательство

4. Аксиома параллелограмма сил
Две силы, приложенные к телу в одной точке, можно заменить их равнодействующей силой, равной векторной сумме этих сил и приложенной к той же точке.
Верно и обратное. Любую силу можно разложить на две (и более) силы по правилу векторной суммы (по правилу параллелограмма), приложенных в той же точке, что и исходная сила.

То есть, если силы и приложены в одной точке, то их можно заменить равнодействующей , приложенной к той же точке. Сумму векторов можно найти двумя способами.
1) Можно вычислить проекции сил на оси прямоугольной системы координат:
.

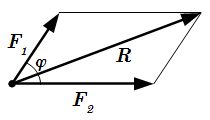
Сложение сил по правилу параллелограмма

2) Можно сложить векторы по правилу параллелограмма (см. рисунок).
;
.
Здесь – угол между векторами и . Точкой обозначено скалярное произведение векторов.

5. Аксиома равенства действия и противодействия (3-й закон Ньютона)
Всякому действию соответствует равное и противоположно направленное противодействие.

То есть если мы возьмем все силы, действующие на тело 2 со стороны тела 1, и объединим их с силами, действующими на тело 1 со стороны тела 2, то получим уравновешенную систему сил.

6. Принцип отвердевания
Если деформируемое тело находится в равновесии, то его равновесие не нарушится, если тело считать абсолютно твердым.

Система сходящихся сил

Система сходящихся сил всегда имеет равнодействующую , равную векторной сумме этих сил:
,
и приложена в точке их пересечения.

Таким образом, проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на оси координат:
;
.

Условия равновесия системы сходящихся сил
Если тело или система тел, на которые действует сходящаяся система сил, находится в покое, то равнодействующая этих сил равна нулю:
.
Это дает три уравнения равновесия:
.

Теорема о трех непараллельных силах
Если твердое тело находится в равновесии под действием трех сил, линии действия двух из которых пересекаются в одной точке, то все силы лежат в одной плоскости и являются сходящимися.

Следствие
Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то эти силы являются сходящимися.

Параллельные силы

Ранее мы отмечали, что система сходящихся сил имеет равнодействующую. То есть такую систему можно заменить одной силой. Приведем еще важные примеры систем сил, имеющих равнодействующую.

Две силы одного направления

Пусть мы имеем две однонаправленные параллельные силы и . Переместим точки их приложения вдоль линий их действия в точки A и B так, чтобы отрезок AB был перпендикулярен силам. Тогда система сил и имеют равнодействующую , приложенную в точке C . Направление равнодействующей совпадает с направлениями и . Абсолютная величина равна сумме сил:
.
Точка приложения C находится между A и B и делит отрезок AB обратно пропорционально модулям сил:
.

Две противоположно направленные силы

Теперь рассмотрим противоположно направленные силы и , различающиеся по величине, . Пусть . Эта система также имеет равнодействующую , направление которой совпадает с направлением большей по модулю силы, а абсолютное значение равно абсолютному значению разности модулей сил:
.
Точка приложения C равнодействующей находится на продолжении отрезка AB , ближе к наибольшей по модулю силе . Расстояния до точек A и B также обратно пропорциональны и :
.

Момент силы относительно точки

Определение

Абсолютное значение момента силы относительно точки O равно произведению силы на плечо этой силы относительно выбранной точки O . Направление момента перпендикулярно плоскости, проходящей через точку O и линию действия силы.
Доказательство

Геометрическая интерпретация

Пусть векторы и расположены в плоскости рисунка. Согласно свойству векторного произведения, вектор перпендикулярен векторам и , то есть перпендикулярен плоскости рисунка. Его направление определяется правилом правого винта. На рисунке вектор момента направлен на нас. Пусть α – угол между векторами и . Абсолютное значение момента:
.

Из точки O проведем перпендикуляр OH к линии действия силы . Из прямоугольника OAH имеем: . Тогда
.
То есть абсолютное значение момента силы относительно точки O равно произведению силы F на плечо |OH| этой силы относительно точки O .

Компоненты момента силы в декартовой системе координат

Выберем декартову систему координат Oxyz с началом в точке O . Найдем компоненты вектора момента силы в этой системе координат относительно ее начала.

.
Здесь – единичные векторы в направлении осей ; – координаты точки A в выбранной системе координат: .

Таким образом, момент силы имеет следующие компоненты:
(М.1) ;
(М.2) ;
(М.3) .
Компоненты представляют собой значения момента силы относительно осей , соответственно.

Свойства момента силы относительно центра

Момент относительно центра O , от силы, проходящей через этот центр, равен нулю.
Доказательство

Если точку приложения силы переместить вдоль линии, проходящей через вектор силы, то момент, при таком перемещении, не изменится.
Доказательство

Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство

То же самое относится и к силам, чьи линии продолжения пересекаются в одной точке.

Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство

Теорема Вариньона о моменте равнодействующей
Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки равен векторной сумме моментов сил системы относительно той же точки.

Пара сил

Из предыдущих формул ⇑ видно, что если противоположно направленные силы имеют равные модули: , то система сил не имеет равнодействующей. Действительно, в этом случае . Пытаясь использовать предыдущие формулы, мы получим деление на нуль. Такую систему сил называют парой сил.

Пара сил – это система из двух сил , равных по абсолютной величине, имеющих противоположные направления, приложенных к разным точкам тела и не лежащих на одной прямой.
Плечо пары сил – это кратчайшее расстояние h между линиями действия сил, входящих в пару.
Момент пары сил – это векторная сумма моментов сил, входящих в пару, вычисленная относительно любой точки. Абсолютное значение момента пары равно произведению силы на плечо пары:
.

Теорема о независимости выбора центра при вычислении момента пары
Векторная сумма моментов сил, составляющих пару, не зависит от выбора точки, относительно которой вычисляются моменты.
Теорема об эквивалентности пар
Две пары, имеющие равные векторы моментов, эквивалентны. То есть у пары можно менять модуль силы и длину плеча, оставляя неизменным ее момент.
Теорема о возможности перемещения пары
Пару сил можно переносить в любом направлении. Другими словами, если пару сил переместить параллельным переносом в любое положение, то она будет эквивалентна исходной паре.
Теорема о сложении нескольких пар
Система нескольких пар сил эквивалентна одной паре, вектор момента которой равен векторной сумме моментов исходных пар.
Условие равновесия пар
Система, состоящая только из нескольких пар, является уравновешенной, если векторная сумма моментов пар равна нулю:
.

Момент силы относительно оси

Часто встречаются случаи, когда нам нужно знать не все компоненты момента силы относительно выбранной точки, а только проекцию момента на выбранное направление.

Момент силы относительно оси, проходящей через точку O – это проекция вектора момента силы относительно точки O , на направление оси.

Свойства момента силы относительно оси

Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство

Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство

Вычисление момента силы относительно оси

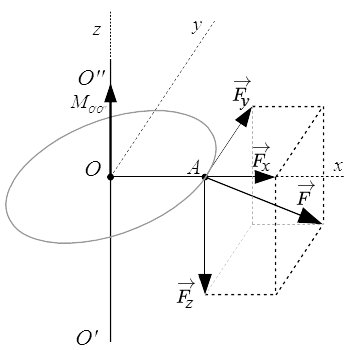
Пусть на тело, в точке A действует сила . Найдем момент этой силы относительно оси O′O′′ .

Построим прямоугольную систему координат. Направим ось z вдоль O′O′′ . Из точки A опустим перпендикуляр AO на O′O′′ . Через точки O и A проводим ось Ox . Перпендикулярно Ox и Oz проводим ось Oy . Разложим силу на составляющие вдоль осей системы координат:
.
Сила пересекает ось O′O′′ . Поэтому ее момент равен нулю. Сила параллельна оси O′O′′ . Поэтому ее момент также равен нулю. По формуле (М.3) находим:
.

Заметим, что компонента направлена по касательной к окружности, центром которой является точка O . Направление вектора определяется правилом правого винта.

Условия равновесия

Главный вектор и главный момент

Подчеркнем, что величина главного момента зависит от выбора центра, относительно которого вычисляются моменты.

Пространственная система сил

Основная форма условий равновесия

Условия равновесия системы сил
Для того, чтобы твердое тело под действием произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы главный вектор и главный момент, относительно произвольной точки C , равнялись нулю:
;
.
Здесь – точка приложения силы , .
Доказательство

Это основная форма условий равновесия. Точка C может, как принадлежать телу, так и находится за его пределами. Обычно центр C выбирают так, чтобы сделать вычисления более простыми. Спроектировав каждое из этих векторных уравнений на три направления, получим шесть уравнений, из которых можно определить шесть неизвестных величин.

Вторая форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
;
;
.
Доказательство

Третья форма условий равновесия

Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
;
;
;
.
Доказательство

Плоская система сил

Все изложенное для пространственной системы сил является применимым и для плоской системы. Направим оси x и y декартовой системы координат в плоскости действия сил, а ось z – перпендикулярно. Тогда z компоненты координат точек и сил равны нулю: . Также равны нулю x, y компоненты моментов сил относительно произвольной точки C : . То есть момент может иметь отличное от нуля значение только для z компоненты. Поскольку z компонента не входит в плоскую систему координат xy , то, в двумерном пространстве, момент силы уже не является вектором, а является скаляром (точнее псевдоскаляром). Его называют алгебраическим моментом силы относительно центра C (или просто моментом силы относительно центра C ), и обозначают символом с маленькой буквы без знака вектора:
.

Величина является моментом силы относительно оси, проходящей через точку C перпендикулярно плоскости действия сил. Момент вычисляют как произведение модуля силы на плечо со знаком плюс или минус:
.
Если, при неподвижном центре C , сила стремится повернуть систему против часовой стрелки, то момент положителен . В противном случае – отрицательный: .

Величину момента от силы , приложенной в точке A , относительно центра C , также можно выразить через компоненты векторов по формуле:
,
где и – координаты точек A и C , соответственно.

Условия равновесия плоского тела

Для плоской системы сил можно составить три уравнения, из которых можно определить три неизвестных величины. Считаем, что сила приложена в точке .

Основная форма условий равновесия
;
;
.

Вторая форма условий равновесия
;
;
.

Третья форма условий равновесия
;
;
;
.

Связи и их реакции

Определения и свойства

Принцип освобождаемости
Всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей и их реакции

Плоские и пространственные задачи

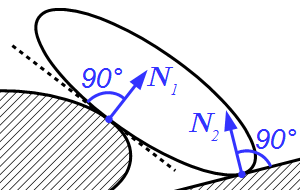
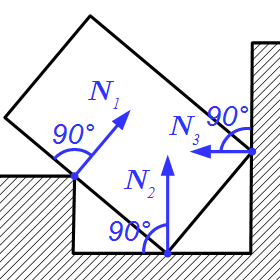
Две гладкие не острые поверхности. Через точку соприкосновения проводим касательную плоскость к этим поверхностям. Реакция является силой, направленной перпендикулярно этой плоскости, то есть, направлена по нормали к обеим поверхностям в точке их соприкосновения.

Одна из гладких поверхностей является острием. Реакция является силой, направленной вдоль нормали не острой поверхности в точке соприкосновения.

Две шероховатые поверхности. То же самое, что и для гладких поверхностей, только в точке соприкосновения добавляем силу трения, лежащую в плоскости касания.

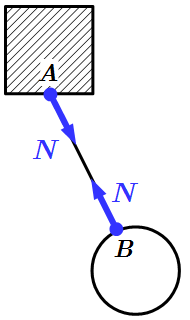
Невесомая нить и стержень. Реакция направлена вдоль нити или стержня. При этом на нить всегда действует сила растяжения. На стержень может действовать как растягивающая, так и сжимающая сила.

Плоские задачи

Следующие связи применяют только в плоских задачах.

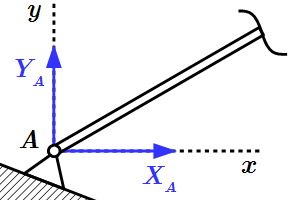
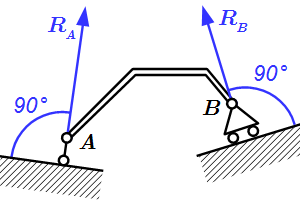
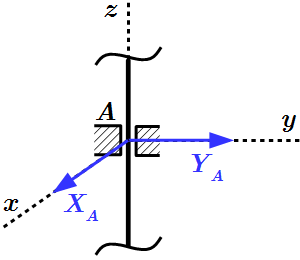
Неподвижный шарнир. Реакция является силой, проходящей через ось шарнира. Обычно ее раскладывают на две составляющие параллельно осям координат.

Подвижный шарнир, или опора на катках. Реакция является силой, которая проходит через ось шарнира перпендикулярно опорной поверхности.

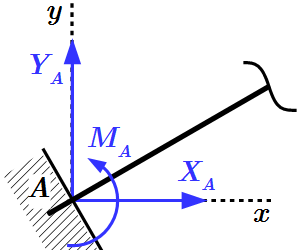
Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно оси, проходящей через точку соединения перпендикулярно плоскости фигуры. Силу обычно раскладывают на две составляющие параллельно осям координат.

Пространственные задачи

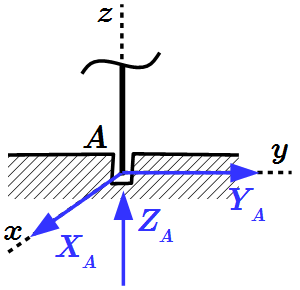
Цилиндрический шарнир или петля. Реакция является силой, проходящей через ось шарнира, перпендикулярно направлению оси. Обычно ее раскладывают на две составляющие параллельно осям координат.

Сферический подшипник или подпятник. Реакция является силой, проходящей через центр подшипника. Обычно ее раскладывают на три составляющие параллельно осям координат.

Заделка. Реакция состоит из силы, проходящей через точку соединения и момента относительно этой точки. Силу и момент обычно раскладывают на три составляющие параллельно осям координат.

Силы трения

Трение скольжения

Рассмотрим тело, которое скользит по поверхности другого тела с отличной от нуля скоростью v под действием внешней силы . Если поверхности абсолютно гладкие, то в точках соприкосновения тел возникает только сила давления N , перпендикулярная плоскости соприкосновения тел. Для шероховатых поверхностей, возникает еще сила трения , параллельная плоскости соприкосновения, направленная в сторону, противоположную скорости движения. Величина силы трения пропорциональна силе давления и не зависит от площади соприкосновения поверхностей:
(Т1) .
Здесь f – безразмерный коэффициент, который называется динамическим коэффициентом трения, или коэффициентом трения скольжения. Он зависит от материалов и обработки соприкасаемых поверхностей и почти не зависит от скорости относительного движения. При расчетах его считают постоянной.

Сила трения скольжения – это сила трения, приложенная к точкам соприкосновения движущихся тел и параллельная плоскости их соприкосновения. То есть это сила, препятствующая скольжению одного тела по поверхности другого. При расчетах, под силой трения скольжения понимают равнодействующую всех сил трения, возникающих в точках соприкосновения тел.

Закон Амонта – Кулона
Сила трения скольжения направлена параллельно плоскости соприкосновения тел в сторону, противоположную их движению, которое возникло бы при отсутствии трения. Она не зависит от площади соприкосновения поверхностей, а зависит от силы давления N одной поверхности на другую, перпендикулярную плоскости соприкосновения тел:
.

Трение сцепления

Теперь рассмотрим статическую задачу. Пусть тело покоится, и на него действуют внешние силы с равнодействующей , приложенной под углом φ к нормали поверхности. Разложим ее на две составляющие: параллельную поверхности, и перпендикулярную . На тело также действуют сила реакции , перпендикулярная плоскости соприкосновения тел, и сила трения , которую при отсутствии скольжения называют силой сцепления. Сила сцепления направлена параллельно поверхности, препятствуя движению. Она может принимать значения от нуля до максимальной величины , определяемой аналогично (Т1):
(Т2) .
Здесь – статический коэффициент трения, который еще называют коэффициентом сцепления. Он не может быть меньше динамического коэффициента трения: .

Если , тело покоится. При этом сила трения сцепления меньше максимальной величины: . При , возникает движение. Когда , сила трения достигает предельной величины, возникает состояние предельного равновесия. Дальнейшее увеличение приводит к потере равновесия.

Сила трения сцепления – это сила трения скольжения, когда относительное перемещение соприкасающихся тел отсутствует.
Предельная сила трения – это максимальное значение силы трения сцепления.
Предельное равновесие – это состояние равновесия, при котором значение силы трения сцепления равно ее максимальному значению.

Из условий равновесия имеем: . Подставим в (Т2):
.
Отсюда получаем, что система будет находиться в равновесии, если
.
Видно, что условие равновесия зависит от угла φ , под которым приложена равнодействующая внешних сил, и не зависит от ее величины. Введем предельный угол трения: . Эту величину также называют просто углом трения. Тогда, условие равновесия можно записать так:
.
Это неравенство определяет конус в пространстве, который называется предельным конусом трения, конусом трения, или конусом сцепления. Если направление силы выходит за пределы этого конуса, то система начинает движение. Если направление силы попадает в конус сцепления, то система остается в состоянии покоя. Такое явление называется заклиниванием механизма.

Заклинивание механизма – это явление в механике, при котором система остается в состоянии покоя при любом, сколь угодно большом увеличении модуля внешней силы.

Условие возникновения движения при наличии трения
Для того чтобы тело начало движение, необходимо и достаточно, чтобы равнодействующая внешних сил находилась вне конуса трения.

Трение качения

Рассмотрим случай, когда одно из тел круглой формы катится без проскальзывания по поверхности другого. С точки зрения механики, такие тела соприкасаются в одной точке A . Площадь их соприкосновения бесконечно мала, в результате чего возникает бесконечно большое давление, которое не могут выдержать реальные материалы. Поэтому вблизи точки соприкосновения тел возникает деформация, которая имеет место только в небольшом участке соприкасающихся тел. В основной части тел, удаленных от точек соприкосновения, деформация практически отсутствует, и их можно рассматривать как абсолютно твердые тела. Тогда систему сил, возникающую в результате соприкосновения, можно привести к некоторой равнодействующей силе . При этом оказывается, что точка ее приложения смещена относительно оси симметрии катящегося тела. Это приводит к появлению момента сил относительно точки A , расположенной на оси симметрии круглого тела. Изучение деформированного состояния выходит за рамки теоретической механики. Поэтому мы приводим лишь результаты, применяемые в расчетах.

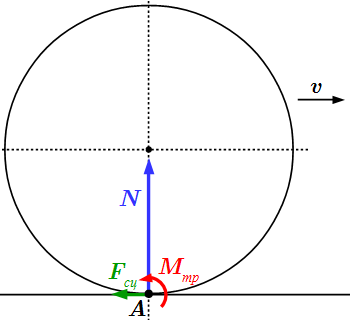
Расчетная схема трения качения.

1. Поскольку деформации, для небольших значений внешних сил малы, то, считают, что они не влияют на геометрические характеристики тел. То есть считают, что тела округлой формы соприкасаются в одной точке.
2. В точке соприкосновения, на тело действуют:
сила давления , перпендикулярная соприкасающимся поверхностям;
сила сцепления , лежащая в касательной плоскости, проходящей через точку соприкосновения поверхностей;
момент силы трения , препятствующий движению.
Максимальное значение момента силы трения определяется по формуле:
,
где δ – коэффициент трения качения, который имеет размерность длины.
3. Коэффициент трения качения зависит от соприкасающихся материалов и состояния их поверхностей. Он не зависит от кривизны поверхностей и угловой скорости вращения тела. А при движении с проскальзыванием, не зависит от скорости скольжения.

Центр тяжести тела

Центр тяжести в пространстве

Пусть тело состоит из n материальных точек. И пусть на каждую точку B_i действует сила тяжести , . Все силы тяжести, действующие на точки, параллельны. Поэтому мы имеем дело с параллельной системой сил. Как и для системы из двух однонаправленных сил, такая система сил имеет равнодействующую. Найдем ее.

Пусть – главный вектор. Поскольку все силы имеют одинаковое направление, то введем единичный вектор , направленный вдоль сил:
. Отсюда .

Найдем момент сил тяжести относительно произвольно расположенного центра O .
,
где
(ЦТ1) .

Отсюда видно, что формула вычисления момента имеет вид формулы момента от одной силы , приложенной в точке C . Точка C , положение которой определяется формулой (ЦТ1), называется центром тяжести тела. Таким образом, равнодействующая отдельных сил тяжести точек тела равна главному вектору силы тяжести, приложенному в центре тяжести. Модуль P равнодействующей называют весом тела.

Если бы мы находили равнодействующую сил тяжести, выполняя эквивалентные преобразования сил, то мы бы нашли только линию действия равнодействующей. Далее, если повернуть тело на некоторый угол, то можно найти другую линию действия равнодействующей. При этом все, подобным образом построенные линии, пересекаются в одной точке, которая и является центром тяжести тела.

Центр тяжести твердого тела – это точка, связанная с телом, через которую проходит линия действия равнодействующей сил тяжести частиц тела, при любом положении тела в пространстве.
Вес тела – это абсолютное значение равнодействующей сил тяжести частиц, составляющих тело.

Координаты центра тяжести определяются по формулам:
(ЦТ2) .
Здесь – абсолютное значение равнодействующей сил тяжести, или вес тела. – координаты точек тела. Эти формулы также можно записать в векторном виде.
.
Центр тяжести C связан с телом. Однако его положение может находиться за его пределами. Например, при наличии полости.

В случае, когда силы имеют другое происхождение, но также имеют одинаковое направление, то мы имеем дело с системой параллельных сил. В этом случае, точка C называется центром параллельных сил.

Для сплошного однородного тела, мы от суммирования переходим к интегрированию. Элементарная сила тяжести выражается через плотность ρ_i элементарной частицы тела, массой , и занимающей объем :
.
Здесь g – ускорение свободного падения. Переходя от суммированию к интегрированию, имеем:
(ЦТ3) .

Центр тяжести плоской фигуры

Рассмотрим плоскую фигуру. Выберем двумерную систему координат Oxy . Тогда положение центра тяжести определяется по тем же формулам (ЦТ2) и (ЦТ3), из которых нужно убрать переменную z .

Однородная фигура

Рассмотрим плоскую однородную фигуру. Для такой фигуры, плотность ρ является постоянной; сила тяжести Δp_i элементарной частицы пропорциональна площади ΔA_i этой частицы: Δp_i = ρΔA_ig . Вес P фигуры пропорционален площади A всей фигуры: P = ρAg .

Подставляя эти величины в формулы, определяющие положение центра тяжести находим:
.
Переходим от суммирования к интегрированию:
.
Мы видим, что сюда не входят плотность ρ и ускорение свободного падения g . Остались величины, зависящие только от геометрии сечения. Таким образом, для тела с постоянной плотностью, центр тяжести является геометрической характеристикой.

В этих формулах, y_C есть алгебраическое расстояние от центра тяжести до оси x ; y_k или y – алгебраическое расстояние элементарного участка до той же оси. x_C , x_k и x – соответствующие алгебраические расстояния до оси y . В этой связи вводят новую геометрическую характеристику сечения, которую называют статическим моментом.

Статический момент относительно некоторой оси – это сумма произведений элементарных площадей , входящих в состав фигуры, на алгебраические значения их расстояний до этой оси.

В рассматриваемом нами случае, статические моменты относительно осей x, y определяются по формулам:
.
Статические моменты широко используются при расчете конструкций. Для стандартных профилей, их значения указываются в соответствующих справочниках.

Центры тяжести простейших фигур

Параллелограмм, прямоугольник, квадрат: в точке пересечения диагоналей.
Треугольник: в точке пересечения медиан, которая делит каждую медиану в соотношении 1:2.
Дуга окружности с центральным углом 2α: .
Круговой сектор: .

Теоремы, применяемые при расчете центра тяжести

Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.

Если однородное тело имеет плоскость симметрии, то его центр тяжести находится в этой плоскости.

Центр тяжести фигуры, составленной из n более простых фигур, определяется по формуле:
(ЦТ4) .
Здесь – площадь всей фигуры; – площадь и координаты центра тяжести простой фигуры, входящей в состав сложной.

Способ отрицательных площадей (объемов)
Если k — я фигура вырезана из объемлющей ее части, то, в формуле (ЦТ4), соответствующая ей площадь считается отрицательной: .

Распределенная нагрузка

Силу тяжести протяженных тел, на схемах, изображают в виде эпюр. Также встречаются подобные силе тяжести параллельные силы, приложенные не в определенных точках тела, а непрерывно распределенные по его поверхности или объему. Такие силы называют распределенными силами или распределенными нагрузками.

Равномерно распределенная нагрузка q (рисунок А). Ее можно заменить равнодействующей силой величины , приложенной в центре тяжести эпюры. Поскольку, на рисунке А, эпюра представляет собой прямоугольник, то ее центр тяжести находится в центре основания эпюры – в точке C : | AC | = | CB | .

Линейно распределенная нагрузка q (рисунок В). Ее также можно заменить равнодействующей. Величина равнодействующей равна площади эпюры:
.
Точка приложения находится в центре тяжести эпюры. Центр тяжести треугольника, высотой h , находится на расстоянии от основания. Поэтому .

Приведение системы сил к центру

Теорема о параллельном переносе силы (лемма Пуансо)
Сила, действующая на данное тело, эквивалентна силе, полученной параллельным переносом исходной силы в любую точку тела и паре сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Теорема о приведении системы сил к заданному центру
Любую систему сил, действующих на данное тело, можно привести к заданному центру O – то есть заменить одной силой, равной главному вектору, приложенной к точке приведения O , и парой сил с моментом M_O , равным главному моменту относительно центра O .

Статические инварианты

Такими инвариантами являются:
1) главный вектор ;
2) скалярное произведение главного вектора на главный момент .
Главный вектор равен векторной сумме всех сил и поэтому не зависит от центра приведения O . Главный момент зависит от положения центра O , относительно которого вычисляются моменты. Но величина его скалярного произведения на главный вектор не зависит от того, относительно какой точки вычисляется главный момент.

Хотя главный вектор не зависит от положения центра O , но величины его проекций на оси координат зависят от выбора системы координат. Поэтому они также не являются инвариантами. По той же причине и направление главного вектора не является инвариантом. Единственной численной величиной, которая не зависит от выбора системы координат, является модуль главного вектора. Но, в математическом отношении, проще иметь дело с квадратом модуля. Поэтому мы выберем его в качестве основного инварианта.

Итак, статическими инвариантами являются следующие величины:
– квадрат модуля главного вектора;
– скалярное произведение главного вектора на главный момент. Инвариантами также являются функции от инвариантов. Например, проекция главного момента на направление главного вектора является инвариантом:
.

Динама

Разложим главный момент на компоненту , параллельную главному вектору , и на компоненту , перпендикулярную :
(П1) .
Тогда .
Отсюда получаем упомянутый выше результат, что инвариантом является алгебраическая величина проекции главного момента на направление главного вектора:
.

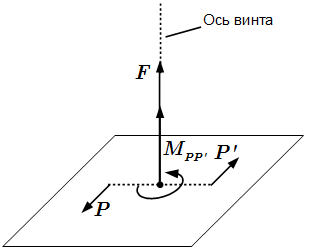
Динама – одна из простейших систем сил.

То есть, при изменении положения центра O , меняется вектор , в то время как вектор остается постоянным. Выбором центра приведения O , можно обратить в нуль. Тогда мы получим систему, состоящую из главного вектора и пары сил с моментом , лежащих в плоскости, перпендикулярной главному вектору. Такая система называется динамой или силовым винтом. Система приводится к динаме, если второй статический инвариант не равен нулю.

Динама – это простейшая система сил, состоящая из силы , приложенной к некоторой точке C , и паре сил, перпендикулярных . При этом момент пары параллелен линии действия силы. Динаму также называют силовым винтом, динамическим винтом, или статическим винтом.
Ось винта – это линия действия силы динамического винта.

Из (П1) мы находим, что минимальное значение модуля момента равно модулю его проекции на направление главного вектора:
.

Центральная ось системы сил

Пусть и – главный вектор и главный момент относительно некоторого центра O , который выберем за начало координат. И пусть второй инвариант отличен от нуля:
.
Найдем положение такой точки C , относительно которой система сил приводится к динаме. Для этого преобразуем главный момент от центра O к C :

.
Отсюда
(П2) .
Для динамы, векторы и направлены вдоль одной прямой. Поэтому
, где λ – некоторое число. Отсюда получаем два уравнения:
(П3) .
Пусть – компоненты вектора . Тогда подставив (П2) в (П3), имеем:
.
Это уравнение прямой в пространстве, которую называют центральной осью системы сил. Относительно точек этой прямой, система сил приводится к динаме, а главный момент имеет наименьшее по модулю значение.

Центральная ось системы сил – это прямая, обладающая тем свойством, что при приведении системы сил к любой из ее точек, система сил является динамой. При этом главный вектор и главный момент динамы параллельны этой прямой, а главный момент имеет наименьшее по модулю значение.

Приведение системы сил к простейшему виду

Пара сил

Пусть .
Тогда . Второй инвариант также равен нулю: . В этом случае, вектор главного момента не зависит от положения центра O . Система сил приводится к паре с моментом .

Если и , то это уравновешенная система сил. Она эквивалентна отсутствию сил.

Равнодействующая сила

Пусть .
В этом случае существует прямая, относительно точек которой главный момент равен нулю:
.
То есть система приводится к одной силе – равнодействующей, равной главному вектору приложенному к любой из точек упомянутой выше прямой. Эта прямая является линией действия главного вектора. Примеры: система сходящихся сил, система параллельных сил. Это системы, которые имеют равнодействующую.

Динама

При , как показано выше, система сил приводится к динаме.

Использованная литература:
А. А. Яблонский, В.М. Никифорова. Курс теоретической механики, часть 1, статика, кинематика. Москва, «Высшая школа», 1966.
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.

Автор: Олег Одинцов . Опубликовано: 03-10-2017 Изменено: 07-05-2020

iSopromat.ru

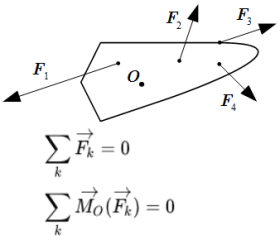
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

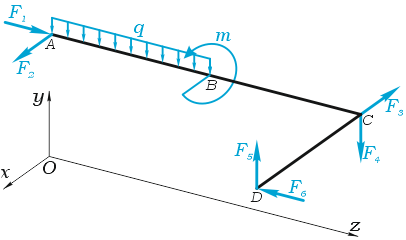
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Пример составления уравнений равновесия

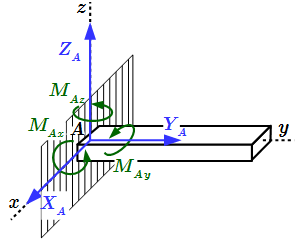
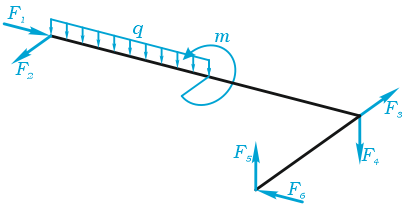
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

• в плоскости xOy:
  
• в плоскости xOz:
  
• в плоскости yOz:
  

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Статика в теоретической механике

Содержание:

Статикой называется раздел теоретической механики, в котором изучаются методы преобразования одних систем сил в эквивалентные им, а также устанавливаются условия равновесия механических систем под действием различных систем сил.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Статика

Изучение этого раздела начнем с рассмотрения основных понятий статики. Как и в каждой естественной науке, в механике для изучения наиболее существенных черт того или иного явления приходится абстрагироваться от менее существенного, отбрасывать второстепенное, то есть вводить абстракции. Первыми такими абстракциями является понятие материальной точки, системы материальных точек и абсолютно твердого тела.

Тело, размерами которого в условиях конкретной задачи можно пренебречь, называется материальной точкой. В отличие от геометрической точки, материальная точка обладает массой данного тела, благодаря чему для нее характерные свойство инертности и способность взаимодействия с другими материальными точками.

Системой материальных точек (механической системой) называется совокупность материальных точек, положения и движения которых взаимосвязаны. Например, изучая движение планет Солнечной системы, их считают материальными точками с соответствующими массами, пренебрегая размерами планет как незначительными по сравнению с расстоянием между ними. всю Солнечную систему рассматривают как систему материальных точек, между которыми действуют силы взаимного притяжения.

Всякое физическое тело в механике представляют как систему материальных точек. Особое значение для теоретической механики имеет неизменная система материальных точек.

Неизменной называется система, которая с течением времени не меняет взаимного
размещение принадлежащих к ней точек. Если постоянная система материальных
точек непрерывно заполняет какую-то часть пространства, то такая система называется абсолютно твердым телом. Из свойств неизменной системы следует, что абсолютно твердым телом называется такое тело, в котором расстояние между его точками остается неизменной при воздействии на него других тел. Иначе говоря, абсолютное твердое тело не меняет своей геометрической формы, то есть не деформируется. В действительности недеформируемых тел в природе не существует. Все физические тела в той или иной степени деформируются. Величины деформаций зависят от материала тел, геометрических размеров и действующих нагрузок. При проектировании инженерных сооружений материал и размеры конструкций отбирают так, чтобы при заданой нагрузке деформации их были незначительными. Вследствие этого при изучении равновесия твердых тел их деформациями часто можно пренебречь и считать их абсолютно твердыми.

В дальнейшем абсолютно твердое тело будем называть твердым телом или телом.

Одним из основных понятий механики является понятие силы. Силой называется количественная мера механического взаимодействия между материальными телами, которая выражает направление и интенсивность этого взаимодействия.

Силы могут возникать как при непосредственном контакте тел (например, сила трения между поверхностями двух тел), так и на расстоянии (например, силы притяжения планет).

Действие силы на тело характеризуется точкой ее приложения, направлением в пространстве и величиной (модулем) силы. Направление, в котором происходит
взаимодействие между телами, называется направлением действия силы. Прямая LM, вдоль которой направлена сила, называется линией действия силы (рис. 1.1).

Точка, в которой происходит взаимодействие между телами (точка контакта), называется точкой приложения силы (точка А). Интенсивность взаимодействия между телами называется величиной (модулем) силы (длина отрезка АВ в соответствующем масштабе на рис. 1.1).

Физическую величину, которая имеет три такие характеристики, как точку приложения, направление в пространстве и абсолютную величину (модуль), изображают вектором. Силу, как векторную величину, будем обозначать, модуль силы — или . Величина (модуль)силы определяется динамически и статически. Согласно динамическому определению, величина (модуль) является числом, которое равно произведению массы
точки на ускорение, которого придает ей сила, то есть (по второму законону Ньютона). Статическое определение силы основано на сравнении данной силы с другой, принятой в выбранной системе единиц. Для этого пользуются динамометром или пружинными весами. Единицей силы в Международной системе единиц принято ньютон — сила, которая массе 1 кг оказывает ускорение

Совокупность нескольких сил, приложенных к телу или механической системы, называется системой сил. Будем обозначать систему с n сил так:.Если векторы сил системы лежат в одной плоскости, она называется плоской, если векторы сил лежат в разных плоскостях, то система сил называется пространственной.

Если, не нарушая кинематической состояния свободного тела, одну систему сил , приложенной к этому телу, можно заменить другой системой, и наоборот, то такие системы сил называются эквивалентными. Их эквивалентность обозначается:

Под кинематической состоянием тела надо понимать состояние его покоя или движения по определенному закону. Если система сил, эквивалентна одной силе , то эта сила называется равнодействующей данной системы сил

Система сил, эквивалентной нулю, называется уравновешенной. Это записывается следующим образом

В статике достаточно часто понятие «уравновешена система сил» заменяют выражением «равновесие сил», или «система сил, находится в равновесии», понимая при этом, что твердое тело под действием системы сил находится в состоянии покоя или инерционного движения.
Замечания. Во инерционным движением (движение по инерции) следует понимать
поступательное прямолинейное равномерное движение.
Содержание статики абсолютно твердого тела составляют две основные задачи.
Первая — задача о эквивалентные преобразования системы сил и замену их
проще, которая имеет важное значение не только в статике, но и в
динамике. Вторая — задача о равновесии систем сил. Основной задачей ее является установление условий, которые должны удовлетворять та или иная система
сил, приложенных к твердому телу, необходимых для его равновесия.

Аксиомы статики

В основе статики лежат экспериментально и логически установлены утверждение (аксиомы), которые отражают свойства сил, действующих на твердое тело.

Аксиома 1 (о двух силы). Две силы, приложенные к твердому телу, будут уравновешенные (эквивалентные нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в разные стороны (рис. 1.2).

Аксиома 2 (о присоединении или изъятия уравновешенных сил). НЕ меняя кинематического состояния твердого тела, к системе сил, действующий на него, можно присоединять или извлекать из нее любую уравновешенную систему сил.

Заметим, что аксиомы 1 и 2 справедливы только для абсолютно твердых тел.

Аксиома 3 (о параллелограмм сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, которая приложена в той же точке и определяется диагональю параллелограмма, построенного на этих силах (рис. 1.3). согласно данной аксиомой, система сил

По правилу сложения векторов равнодействующая равна геометрической сумме этих сил:

Модуль равнодействующей определяется формуле:

где α — угол между векторами

Аксиома 4 (о равенстве действия и противодействия). Силы взаимодействия двух тел ровно по модулю и направлены по одной прямой в противоположные стороны (рис. 1.4).

Если тело А действует на тело В с силой , то тело В действует на тело А с силой ,причем и Однако эти силы не является уравновешенным, так как приложены к разным телам, то есть система сил , не эквивалентна
нулю. Эта аксиома является одним из основных законов механики (третий закон Ньютона).

Прежде чем перейти к формулировке двух последних аксиом статики, введено понятие связей и реакций связей.

Тела в природе можно разделить на свободные и несвободные. Свободными называются тела, которые под действием той или иной системы сил могут перемещаться в пространстве в любом направлении. Тело, движение которого в пространстве ограничен
другими телами, называется несвободным. Тела, которые ограничивают движение данного
тела в пространстве, называются связями.

Пусть движение некоторого несвободного твердого тела ограничено определенными связями. Очевидно, между телом и связями существуют механические взаимодействия.
Влияние тела на вязь называем действием, а влияние связи на тело — противодействием. Противодействия связей, наложенных на это твердое тело, называются реакциями связей. Иными словами, реакция связи — это сила, с которой связь действует на тело.

Она направляется противоположно тому направлению, в котором вязь противодействует возможному движению тела.

Аксиома 5 (принцип затвердевания).

Равновесие материального объекта не нарушится при наложении на него дополнительных стационарных связей. Частичным случаем аксиомы есть утверждение: равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым.

Этот принцип имеет большое значение при изучении равновесия тел, которые деформируются. Из него следует, что условия равновесия сил, приложенных к абсолютно твердого тела, распространяются и на изучение равновесия не абсолютно твердых тел, то есть принцип устанавливает связь между статикой абсолютно твердого тела и статикой тел, которые деформируются.

Условия равновесия сил, приложенных к твердым телам, являются необходимыми, но не являются достаточными для деформируемых тел. Например, для равновесия невесомого стержня необходимо и достаточно, чтобы силы, приложенные к его концам, были взаимно уравновешены (рис. 1.5, а).

Однако для невесомой нити этого условия недостаточно. Необходимо, чтобы силы, действующие на нить, были только растягивающими (рис. 1.5, б), в то время как для стержня они могут быть и сжимающими.

Статика твердых тел используется при изучении равновесия деформируемых тел в сопротивлении материалов и строительной механике.

Поскольку в статике устанавливаются условия равновесия в основном для свободных тел, а в большинстве технических задач встречаются несвободные твердые тела, то для использования этих условий в несвободных телах следует применить аксиому связей, или так называемый принцип освобождения от связей.

Аксиома 6 (принцип освобождения от связей). Не меняя кинематической состояния тела, всякое несвободное тело можно рассматривать как свободное, если отбросить связи, а их воздействие на тело заменить реакциями связей.

Простейшие теоремы статики

Теорема 1.1 (о скользящем векторе силы). Не меняя действия силы на твердое тело, точку приложения силы можно переносить по линии ее действия.

Доказательство. Пусть на абсолютно твердое тело действует сила , приложенная в
точке А (рис. 1.6, а).

Возьмем на линии действия силы какую-нибудь точку В и приложим к ней две уравновешенные силы и , которые численно равны силе и удовлетворяют условию уравновешенности: (рис. 1.6, б). Согласно аксиомы 2, такое присоединение не нарушает кинематической состояния тела, то есть система сил будет эквивалентна исходной системе сил . поскольку силы и взаимно уравновешиваются (аксиома 1), их, согласно аксиомы 2, можно отбросить, и тогда получим одну силу, которая приложена в точке В (рис. 1.6, в). Итак, мы получили, что

Поскольку, то можно считать, что сила является силой , которая перенесена вдоль линии действия из точки А к точке В. Теорема доказана.

С доказанной теоремы следует, что, нарушая кинематической состояния абсолютно твердого тела, силы, приложенные к нему, можно переносить вдоль их линий действия в любые точки тела. Это означает, что сила в статике является скользящим вектором.

Теорема 1.2 (о трех непараллельных силах). Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия всех трех сил пересекаются в одной точке.

Доказательство. Пусть на твердое тело, находящееся в равновесии, действует система трех сил , линии действия двух из которых, например и , пересекаются в точке А. Перенесем силы и до точки А и заменим равнодействующей согласно аксиомы 3 о параллелограмм сил (рис. 1.7).

Система трех сил, свелась к эквивалентной системе двух сил, которая является уравновешенной, так по условию теоремы тело, на которое они действуют, находится в равновесии. В соответствии с аксиомы 1, такие две силы должны быть направлены по одной прямой, проходящей через точки их приложения. Это означает, что линия действия силы должна пройти через точку А приложения силы , то есть точку пересечения линий действия сил и . Итак, три линии действия сил пересекутся в одной точке. Теорема доказана.

Механические связи и их реакции

Конструктивно связи могут быть выполнены в виде различных опор, шарнирных соединений, гибких элементов (веревки, канаты, цепи и т.д.).

Будем считать, что связи выполнены из абсолютно твердых материалов и трения в местах соединения их с основным телом, рассматривается в равновесии, незначительное, а поэтому им можно пренебречь. Такие связи, в которых игнорируется трение, будем называть идеальными. В случае, когда тело может катиться без скольжения по поверхности, связь также считается идеальной.

Рассмотрим основные типы связей.

Гладкая опорная поверхность

Эта связь является идеальной поверхностью, то есть поверхностью без трения. Например, зеркальная поверхность, хорошо отшлифована
металлическая поверхность, ледяная поверхность и тому подобное. Точка контакта A (рис. 1.8) основного тела K и связи может свободно скользить по поверхности связи, но по нормали к этой поверхности ее движение ограничено. Поэтому реакция гладкой опорной поверхности направлена ​​по нормали n к общей касательной плоскости , проведенной в точке A контакта тела и связи, и приложена в этой точке. Направление реакции противоположный направлению, в котором связь ограничивает движение тела K. реакция называется нормальной реакцией.

Как отдельные случаи такого типа связей является гладкая опорная плоскость (Рис. 1.9) и случай опоры тела на ребро или точку (рис. 1.10).
Если одна из соприкасающихся поверхностей является ребром (опора А на рис. 1.10), то
реакция направляется по нормали к второй поверхности.

Гибкая связь

Гибкие связи реализуются с помощью нитей, шнурков, цепей, канатов и тому подобное. Считаем их нерастяжимыми и невесомыми. Гибкие связи не дают возможности удаляться телу K от точек их крепления (Точек C и D на рис. 1.11.). Поэтому реакция гибкой связи направляется по ней от точки соединения тела и связи к точке закрепление связи с неподвижной поверхностью. Следует заметить, что гибкие связи работают только на растяжение.

Цилиндрический шарнир (подшипник)

Эта связь реализуется с помощью двух
цилиндров (рис. 1.12, а). На теле 1, равновесие которого рассматривается, выполненная цилиндрическая поверхность, которую называют осью или пальцем, а в теле 2, которое называют обоймой или втулкой, сделано цилиндрическое отверстие. Обе цилиндрические поверхности имеют общую геометрическую ось на которой лежит точка O центр шарнира. цилиндрический шарнир, или просто шарнир, осуществляет такое соединение тел, при котором возможен поворот тела K вокруг оси цилиндра 2 и движение вдоль этой оси.

Если пренебречь трением между поверхностями цилиндров, то реакция неподвижной цилиндрической поверхности тела 2 направлена по нормали к этой поверхности и приложена в той точке A, в которой палец тела 1 под действием внешней нагрузки к ней прижимается (рис. 1.12, б), а следовательно, лежит в плоскости, перпендикулярной к общей геометрической оси цилиндров. Линия действия реакции пересечет эту ось, то есть пройдет через центр О шарнира. Величину и направление реакции заранее указать
невозможно, так как они могут быть разными в зависимости от внешнего нагрузки. Поэтому при освобождении тела от такой связи реакцию, которую прикладывают в центре шарнира В, целесообразно заменить двумя составляющими и (рис. 1.12, в), направленными вдоль осей координат. тогда составляющие реакции и неизвестны лишь при алгебраической величиной. Решая конкретную задачу, находят алгебраические значения и .

Величина и направление реакции определяются по формулам:

Если величины или являются отрицательными, то их направления противоположны
принятым (рис. 1.12, в).

На принципе цилиндрического шарнира построено шарнирно-неподвижные и шарнирно-подвижные опоры.

Шарнирно-неподвижная опора

По своей конструкции эта опора является цилиндрическим пальцем 1 (рис. 1.13), который соединяет две обоймы: верхнюю 2, что
скреплена с телом K, которое рассматривается в равновесии, и нижнюю 3, которая закреплена на устойчивую поверхность. На рис. 1.13, а опору показано в разрезе. Такая опора работает как цилиндрический шарнир. Поэтому реакция шарнирно-неподвижной опоры будет лежать в плоскости, перпендикулярной оси цилиндрического пальца, и при
решении практических задач эту реакцию представляют двумя составляющимии
(рис. 1.13, б). Схематично шарнирно-неподвижную опору изображают в виде, показанном на рис. 1.13, б, в.

Шарнирно-подвижная опора

Шарнирно-подвижная опора по своей конструкции аналогична предыдущей. Разница лишь в том, что нижняя обойма 3 поставлена на катки 4 (рис. 1.14, а), которые дают возможность перемещать тело K параллельно неподвижной опорной поверхности. линия действия реакции шарнирно-подвижной опоры проходит через центр шарнира и перпендикулярной опорной плоскости. Схематично шарнирно-подвижная опора изображается в виде, показанном на рис. 1.14, б, в.

Сферический шарнир

Такая связь является шаром,расположенным в сферической
полости (рис. 1.15, а).

Если тело K прикрепить с помощью такого шарнира к неподвижной поверхности, то центр O шарнира не может осуществить никакого перемещения в пространстве, то есть будет неподвижным, а тело может возвращаться произвольно вокруг него. Линия действия реакции сферического шарнира будет направлена по нормали к сферических поверхностей, то есть пройдет через центр O шарнира. реакция сферического шарнира имеет произвольное направление в пространстве и определяется в каждом конкретном случае в зависимости от заданных сил. Практически реакцию сферического шарнира раскладывают на три составляющих (рис. 1.15, б). Величину и направление реакции определяют по формулам:

Подшипник и подпятник

Подшипник является разновидностью цилиндрического шарнира. Схематично подшипник изображается так, как показано опору B на рис. 1.16, а. Реакция подшипника В лежит в плоскости, перпендикулярной к оси подшипника, и при практическом решении задач ее представляют двумя составляющимии . Величина и направление реакции подшипника определяются зависимостями типа (1.3).

Подпятник является сочетанием подшипника с опорной плоскостью, ограничивающей перемещение тела K вдоль оси подшипника в сторону опорной плоскости (опора A на рис. 1.16, а).

Реакция подпятника A состоит из нормальной реакции опорной плоскости и двух составляющих реакции подшипника и . Величина и направление равнодействующей реакции подпятника определяется по формулам типа (1.4).

Идеальная стержневая связь

Связь реализуется в виде невесомых и ненагруженных внешними силами стержней. Концы стержней прикреплены к телу, для которого они являются связями, и к неподвижной основы с помощью цилиндрических или сферических
шарниров, размерами которых и трением в которых пренебрегаем. Такие шарниры называются идеальными точечными, а стержни — идеальными шарнирно-закрепленными.

Пусть для тела K, которое находится в равновесии, идеальные стержни АВ, СD и EH есть связями (рис. 1.17). Каждый из стержней является телом, которое находится в равновесии под действием двух сил, приложенных в точечных шарнирах. Если стержень находится в равновесии, то на основании аксиомы 1 — эти силы должны быть направлены по одной прямой. Другими словам, силы должны действовать по прямой, соединяющая точечные шарниры.

На основании аксиомы 4 реакции реакции являются противодействием связей на тело, а значит, они также будут направлены вдоль прямой, соединяющей точечные
шарниры. Это справедливо как для прямолинейных , так и для
криволинейных стержней. Следовательно, реакция идеального шарнирнозакрипленого стержня направляется по прямой, соединяющей центры точечных шарниров.

Стержневые связи работают на растяжение и на сжатие. Реакцию растянутого стержня принято направлять от его конца до середины, а реакцию сжатого стержня — в противоположном направлении (Рис. 1.17).

Во многих задачах невозможно заранее установить, как работает стержень — на растяжение или на сжатие. Поэтому, решая такую задачу, считают, что стержни работают на растяжение. Если в результате решения задачи окажется, что значение реакций некоторых стержней отрицательные, то эти стержни сжимаются.

Жесткое защемление

Такой тип связи реализуется в виде неподвижного соединения тела с основанием (связью) (рис. 1.18, а). Эта связь ограничивает не только линейное перемещение тела в опоре, а также поворот тела относительно связи. Поэтому реакции жесткого защемления состоят из силыи пары сил с моментом , величины и направления которых зависят от активных сил, приложенных к телу K, и заранее неизвестны (Рис. 1.18, а). Момент называется моментом защемление или реактивным моментом (он будет рассмотрен в разделе 4).

В случае, когда активные силы, действующие на тело, размещенные в одной плоскости (плоская задача), реакция и пара сил с моментом находятся в этой же плоскости. реакцию при этом представляют в виде составляющих (рис. 1.18, б).

В случае пространственной задачи реакцию жесткого защемления раскладывают на три составляющие , а реактивный моментпредставляют в виде трех пар сил с моментами (Рис. 1.18, в).

Классификация сил, приложенных к точкам механической системы

Силы, действующие на точки механической системы, могут по-разному влиять на кинематический состояние как отдельных точек, так и всей системы. Поэтому целесообразно разделить их на различные группы в зависимости от характера этого
воздействия.

Силы классифицируются по двум различным признакам. По первому признаку поделим силы на внешние и внутренние.

Внешними называются силы взаимодействия между точками данной механической
системы и точками, которые не принадлежат этой системе.
Внутренними называются силы взаимодействия между точками данной механической
системы.

Разделение сил на внешние и внутренние относительно. Покажем это на примере: если рассматривать Солнечную систему как систему материальных точек, то силы взаимодействия между планетами будут внутренними. Если же рассмотреть систему Солнце — Земля, то силы притяжения, действующие на эту систему со стороны других планет, будут внешними. Итак, мы видим, что внутренние силы одной механической системы можно перевести в категорию внешних, но относительно другой механической системы.

По второму признаку силы, действующие на невольную механическую систему, делятся на активные и реакции связей, которые отличаются по своей природе.

Активные или заданные силы могут вызвать изменение кинематической состояния механической системы и вызывают реакции связей. Модуль и направление каждой активной силы известны и не зависят от других сил, действующих на систему.

Реакции связей — это силы, возникающие в опорах при действии активных сил.
Реакции связей не могут изменить кинематической состояния тела. Поэтому они
и называются пассивными силами.

Разделение сил указанными способами вполне независим. Реакции связей и активные
силы могут быть как внутренними, так и внешними.

В качестве примера рассмотрим раму (рис. 1.19), состоящий из двух частей, соединенных
между собой шарниром в точке С. На нее действуют силы , которые являются внешними активными силами. Реакции в опорах А и В будут внешними силами. Реакция в шарнире С — внутренняя сила.

Статика твердого тела

Расчетно-графическая работа по статике твердого
тела предусматривает решение задач на следующие темы:
(см. раздел. стр. 61).

• выделение объекта равновесия и расстановка активных сил и реакций связей (тема С1) (задачи 1-8);
• равновесие тела под действием системы совпадающих сил на плоскости и в пространстве (тема С2) (задачи 1, 2);
• равновесие тела под действием произвольной плоской системы сил (тема С3) (задачи 3, 4 5);
• равновесие тела под действием произвольной пространственной системы сил (тема С4) (задача 6).

Выполнение расчетно-графической работы необходимо начинать с повторения теоретического материала, приведенного для каждого изучаемого раздела. Затем
необходимо разобраться в решении соответствующей задачи, что приводится для примера, обращая особое внимание на методические рекомендации по их решению.

Кроме того для самостоятельного выполнения расчетно-графической работы по статике необходимо иметь соответствующую математическую подготовку, поскольку
решение задач требует умения вычислять проекции векторов на координатные оси и плоскости, находить сумму векторов геометрически (построение векторного треугольника или многоугольника) и аналитически (по проекциям на координатной оси), нужно уметь свободно пользоваться системой прямоугольных декартовых координат на плоскости и в пространстве.

Варианты заданий по статике (с. 64-94) и исходные данные к ним (с. 95-106) приведены в приложениях к статике.

Вариант задания, который выбирает студент для выполнения, соответствует его порядковому номеру в списке группы, или задается преподавателем. Кроме того, преподаватель, руководствуясь собственными соображениями, может выдавать
задания комбинируя их из задач различных вариантов. Например, задача 1 из 1-го варианта, задача 2 из 5-го варианта и т.д.

Основные понятия и аксиомы статики

В теоретической механике используются абстрактные представления о материальной точке и абсолютно твердом теле.

Материальной точкой называется материальное тело, размерами которого в условиях задачи, что рассматривается, можно пренебречь.

Принимается, что в материальной точке сосредоточенна вся масса тела и к ней прикладывается сила притяжения тела.

Абсолютно твердым называется такое тело, в котором расстояния между любыми двумя его точками при всех условиях остается неизменным (иначе говоря, тело не деформируется).

Силой в механике называют количественную меру механического взаимодействия двух материальных тел.

Единицей измерения силы в системе СИ является 1 Ньютон (Н), определяемый как сила, предоставляющая телу массой 1 кг ускорения

Сила — векторная величина и ее действие на тело определяется:
— точкой примера,
— направлением (линией действия),
— величиной (числовым значением

Совокупность сил, приложенных к данному телу, называется системой сил.

Система сил, под действием которой тело находится в равновесии, называется уравновешенной, а само тело — объектом равновесия.

Системы сил, которые оказывают одинаковое механическое действие на одно и то же твердое тело, называются эквивалентными системами сил.

Если есть сила, которая действует на тело так же, как и заданная система сил (то есть, эквивалентная ей), то такую силу называют равнодействующей данной системы сил.
Равнодействующая уравновешенной системы сил равна нулю.

Аксиомы статики

Решение задач статики основано на использовании ряда аксиом и теорем.

Аксиома 1. (Первый закон Ньютона). Изолированная от внешнего действия материальная точка, или такая, на которую действует эквивалентная нулю система сил, находится в состоянии покоя или движется прямолинейно и равномерно.

Аксиома 2. Две силы, которые приложенные к абсолютно твердому телу, взаимно уравновешиваются тогда и только тогда, когда они одинаковы по модулю и действуют вдоль одной прямой в противоположные стороны.

Аксиома 3. Присоединение или отвержение уравновешенной системы сил не меняет действие заданной системы сил на абсолютно твердое тело.

Следствие с аксиом 2 и 3. Не изменяя действие заданной системы сил на абсолютно твердое тело, точку). приложение каждой силы можно переносить вдоль линии ее действия в любую точку тела.

Аксиома 4. (параллелограмм сил). Равнодействующая двух сил, что приложена к одной точке абсолютно твердого тела (рис.С1.1), приложенная к той же самой точке и
изображается диагональю параллелограмма который построен на заданных силах, как на сторонах, и модуль которого равен:

Аксиома 5. Силы, с которыми действуют между собой два тела, всегда равны друг другу по модулю, направлены вдоль одной прямой в противоположные стороны и приложенные к разным телам.

Аксиома 6. Равновесие нетвердого (такого, что деформируется) тела, на которое действует заданная система сил, будет сохраняться, если оно мгновенно затвердеет.

Реакции связей

В задачах на равновесие тел в основном рассматриваются несвободные твердые тела, то есть такие, что находятся под действием других тел, которые ограничивают перемещение данного тела и называются связями.

Вязи действуют на рассматриваемое тело с некоторой силой, которую называют реакцией связей. Для каждой реакции, как и любой силы, надо определить ее величину, направление и точку приложения.

Аксиома 7. (Аксиома связей). Любое несвободное тело можно освободить от вязей, если заменить их действие реакциями, после чего рассматривать тело как свободное, которое находится в равновесии под действием заданных сил и реакций.

Несмотря на большое количество физически существующих вязей, большинство из них можно свести к следующим случаям.

Гладкая поверхность

В том случае, когда сила трения, возникающая между телом и поверхностью связей, незначительная и ею можно пренебречь, то поверхности тела и связей называют гладкими (или идеальными).

Если тело опирается на такую поверхность (рис.С1.2), то реакция которая возникает в точке А соприкосновения, всегда направленна вдоль нормали к общей касательной плоскости между поверхностями связей и тела в сторону, противоположной тому, куда связь не дает двигаться телу.

В том случае, когда одна поверхность (тела или связи) вырождается в точку, то реакция будет направлена перпендикулярно к поверхности, которая существует (рис.С1.3).

Гибкая связь

Это связь, выполненная в виде гибкой нерастяжимой нити (веревка, канат, трос, цепь), и не позволяет телу удаляться от точки подвеса нити с направлением АМ (рис.С1.4). Таким образом, реакция натянутой нити направлена вдоль нити от тела к точке ее подвеса.

Цилиндрический шарнир

Цилиндрическим шарниром (рис.С1.5) называется соединение двух тел, которое допускает только вращение одного тела или обоих тел вокруг центра шарнира (точка А) в одной плоскости.

На рис.С1.5,а показана конструкция цилиндрического шарнира, а на рис.С1.5,б — его условное изображение на схемах.

Цилиндрическая шарнирно-неподвижная опора

Шарнирно-неподвижная опора образуется путем неподвижного закрепления одной из частей шарнира и препятствует любому поступательному движению тела, но позволяет ему свободно вращаться вокруг шарнира. Центр шарнира определяет точку приложения опорной реакции (черт. С1.6, а, б), а ее величина и направление являются неизвестными.

При решении задач реакцию , как правило, раскладывают на две составляющие (рис.С1.6, а), которые направляют по осям выбранной системы координат:
за осью за осью

Цилиндрическая шарнирно-движущаяся опора

Шарнирно-подвижная опора отличается от шарнирно-неподвижной тем, что нижняя ее часть установлена на катки. Такая опора не препятствует перемещению механической
системы в направлении качения катков, но препятствует в перпендикулярном. Поэтому реакция этой опоры направлена по нормали к поверхности качения. На рис. С1.7,а показано конструкцию шарнирно-подвижной опоры, а на рис. С1.7,б — ее условное изображение на чертежах и схемах.

Невесомый (идеальный) стержень

На рис.С1.8 показано закрепление груза G за помощью двух невесомых стержней СА и СВ.

Каждый из этих стержней на концах (кстати — необязательно на концах) имеет
цилиндрические шарниры, с помощью которых присоединяется к другим узлам конструкции.

Если силами тяжести стержней и силами трения в шарнирах пренебречь, то
каждый стержень будет находиться в равновесии под действием двух сил, реакций
шарниров, которые, исходя из второй аксиомы статики, направленные вдоль линии, которая соединяет шарниры. Эти силы могут как растягивать соответствующий стержень так и сжимать

Жесткое закрепление

Балка АВ (рис.С1.9) одним своим концом жестко закреплена (замурована) в стенку. Если на балку действуют внешние силы, то в месте закрепления возникают: реакция (поскольку жесткое закрепление препятствует любому поступательному движению тела) и пара сил с моментом закрепление (поскольку жесткое закрепление не позволяет телу свободно вращаться).

Модули и направления реакций и неизвестные. Реакцию как правило,
раскладывают на две составляющие, которые направляют по осям выбранной системы координат и а направлением момента закрепления задаются произвольно.

Сферический шарнир (подпятник)

Сферический шарнир ( шаровая опора) допускает свободное
вращение стержня в пространстве вокруг центра (точки О)
шарнира (рис.С1.10, а).

Реакция сферичного шарнира проходит через центр шарнира и неизвестна по направлению и величиной. При решении задач ее целесообразно раскладывать на три составляющие по направлениям выбранной пространственная система координат

Подпятник (рис.1.10, б), или опорно-упорный подшипник, как и сферический шарнир, закрепляет неподвижно одну из точек твердого тела.

В подпятнике реакция проходит через неподвижную точку О и
неизвестную ни по модулю, ни по направлению. Можно посоветовать раскладывать реакцию на составляющие вдоль осей прямоугольной система
координат

Виды нагрузок, действующих на тело

Сосредоточенная сила действует на тело по площади, размерами
которой по сравнению с площадью поверхности тела можно пренебречь, и поэтому условно считают, что сила приложена в точке. Сосредоточенные силы обозначают большими латинскими буквами (и др.). Единицей измерение сосредоточенной силы — является Ньютон (Н).

Распределенная сила действует на части длины или на всей длине балки. Балкой называется тело, у которого один размер (длина) гораздо больше двух других (ширины и
высоты). В зависимости от характера нагрузки эти силы делятся на равномерно и неравномерно распределенные.

Величина равномерно распределенной силы (рис.С1.11, а), действующая на единицу длины балки, называется интенсивностью нагрузки и обозначается буквой
.

Единицей измерения интенсивности распределенной нагрузки является Ньютон разделен на метр

Равномерно распределенную силу при решении задачи надо заменить сосредоточенной силой которая по модулю равна и приложена посередине отрезка АВ.

Для нагрузки, распределенной по закону «треугольника» (рис.С1.11, б), интенсивность представляет собой величину переменную и растет от нуля до максимального значение

Равнодействующая такой распределенной нагрузки равняется и приложена на расстоянии от стороны ВС треугольника АВС.

Парой сил (рис.С1.12,а) называется нагрузка в виде двух одинаковых по модулю сил направленных в противоположные стороны и линии действия которых параллельны и не лежат на одной прямой.

Пара сил задается моментом М и изображается на чертеже схематично
(рис.С1.12, б). Единицей измерение момента пары сил является Ньютон на метр

Момент пары считается положительным, если пара стремится возвращать тело, на которое действует, против хода часовой стрелки, и отрицательным — в противоположном случае (на рис.С1.12,б —

Образец выполнения и решения задач на темы С1

Выделение объекта равновесия и расстановка сил, что на него действуют

Для каждого задания указано одно или несколько объектов равновесия. Цель работы заключается в том, чтобы для указанного объекта равновесия показать активные силы и
реакции связей, которые на него действуют.

Задача 1
Задано: Объект равновесия — точка В; АВ — невесомый стержень; ВС и ВD — нити (рис.1).

Точка В находится в равновесии под действием реакции нити ВС, направленной вдоль
нее к точке С; натяжение нити ВD, направленного вдоль нее к точке D; реакции невесомого стержня АВ, направленной вдоль оси стержня.

Модуль нити можно определить, рассмотрев равновесие тела G (рис.2). Тело G находится в равновесии под действием двух сил: веса направленного вертикально вниз, и реакции нити направленной вдоль нити вверх. По второй аксиоме статики Таким образом, натяжение нити равно весу тела G, то есть

Задача 2
Задано: объект равновесия — шарнир D; AD, BD – невесомые стержни; DC, DE — нити (рис.1).

Шарнир D находится в равновесии под действием: веса груза которую, учитывая, что направление линии действия силы и направление нити DE совпадают, можно перенести в точку D; силы натяжения нити DC, направленной вдоль нити к точке С; реакций и стержней AD и BD, направленных вдоль осей стержней.

Задача 3

Задано: объект равновесия — балка АВ (рис.1) весом P; DE, BK — нити.
Балка находится в равновесии под действием: веса которая приложена посередине балки АВ; натяжения нити DE, направленной к точке подвеса Е нити; натяжения нити ВК, направленной к точке К и при модуле равной G (см. задачу 1); реакции цилиндрического шарнира A, которая раскладывается на две составляющие вдоль осей координат и

Задача 4

Задано: объект равновесия — балка АВ весом Р. Балка АВ находится в равновесии под действием силы притяжения которая приложена к середине балки; равномерно разделенной нагрузки интенсивностью действие которой можно заменить сосредоточенной силой приложенной в середине участка CB; силы которая приложена под углом к оси балки; реакции жесткого закрепления, которая
разложена на составляющие и по осям выбранной системы координат и пары сил с моментом закрепления

Задача 5

Задано: сложенную конструкцию (рис.1), которая состоит из балки АВ весом и балки CD весом Рассмотреть объекты равновесия: конструкцию в целом; балку АВ; балку СD.

1. Конструкция АВСD (рис.1) находится в равновесии под действием: веса
балки АВ; веса балки СD; веса груза реакции опорной поверхности реакций цилиндрических шарниров А и С, разложенных на составляющие
и Точка В этом случае представляет собой внутреннюю точку объекта равновесия и реакция в ней не изображается .

2. Балка АВ (рис. 2) находится в равновесии под действием: силы веса приложенной посередине АВ; силы тяжести груза; реакции которая заменяет действие отброшенной балки CD и которая направлена перпендикулярно к ней; реакции
шарнира А, разложенной на составляющие и

3. Балка СD (рис. 3) находится в равновесии под действием: силы тяжести приложенной посредине СD; реакции гладкой поверхности направленной перпендикулярно опорной поверхности; реакция по пятой аксиоме статики (раздел С1.1); реакция цилиндрического шарнира С, разложенная на составляющие и по осям выбранной системы координат.

Внимание! Для упрощения решения задачи в случае составной конструкции желательно выбирать единую систему координат для всех объектов равновесия.

Задача 6

Задана сложенная конструкция (рис.1), в которую входят невесомые балки АВ и ВС, соединенные шарниром В.

Рассмотреть объекты равновесия: конструкцию в целом; балку АВ; балку ВС.

1. Балка АВ (рис.2) находится в равновесии под действием: распределенной нагрузки интенсивностью действие которого можно заменить сосредоточенной силой что будет приложена посередине отрезка АЕ; реакции шарнирно-подвижной опоры направленной перпендикулярно к опорной поверхности под углом оси балки; натяжения нити который по модулю равен G; реакции шарнира В, разложенной на составляющие и по осям выбранной системы координат

2. Балка ВС (рис.3) находится в равновесии под действием: реакции шарнира В, разложенной на две составляющие и натяжение нити
(при этом ); пары сил с моментом М; реакции закрепления в

точке С, которая раскладывается на две составляющие силы и по осям выбранной системы координат и пару сил с моментом 3. Конструкция АВС (рис.4) находится в равновесии под действием следующих сил: реакций, натяжения нитей, сосредоточенной силы заменяет действие распределенной нагрузки; пары сил с моментом М.

Задача 7
Объект равновесия — прямоугольная плита АВСD (рис. 1) весом Р.

Точка А — центр сферического шарнира, петля В — цилиндрический шарнир, ЭС — невесомый стержень.

Плита АВСD находится в равновесии под действием: тяжести приложенной в точке

пересечения диагоналей прямоугольной плиты; реакции невесомого стержня, направленной вдоль стержня СЕ; реакции цилиндрического шарнира В, разложена на две составляющие по осям координат, реакции сферического шарнира А, что разложена на три составляющие по осям координат,

Задача 8

Объект равновесия — невесомый вал АВ (рис 1). А, В — подшипники, FDCE — ременная передача. Вал АВ находится в равновесии под действием силы тяжести груза Которая направлена ​​вдоль нити, наматывается на барабан; сил натяжения и веток паса CE и DF ременной передачи; реакций подшипников (Цилиндрических шарниров) А и B, которые разложены на составляющие и По осям выбранной системы координат

Определения, аксиомы и простейшие теоремы статики

Краткие исторические сведенья:

Научные основы статики заложены еще греческим ученым Архимедом (287-212 гг. до н.э.) Он изложил теорию равновесия рычага, который находится под действием параллельных сил, создал учения о центре тяжести, а также исследовал равновесие тел, которые плавают в жидкости.

В геометрическую статику значительный вклад сделали французские ученые П. Вариньен (1654-1722) и Л. Пуансо (1777-1859)

Основоположником аналитической статики является великий французский математики и механик Ж. Лагранж (1736-1813). Дальнейшее развитие аналитической статики связано с именем великого русского математика и механика Н. В. Остроградского (1801-18161) В обосновании аксиоматики статики важную роль сыграли Л. Эйлер (1707-1783). М. Е. Жуковский (1847-1921), С. О. Чаплыгин (1869-1942), В. Г. Имшенецкий В. Г. (1932-1892), О. И. Сомов (1815-1876).

Значительный вклад в развитие графостатики сделал В. Л. Кирпичёв (1845-1913)

Предмет статики. Основные определения и понятия

Статикой называется раздел теоретической механики, в котором изучаются методы преобразования одних систем сил в другие, эквивалентные им, а также условия равновесия систем сил, которые действуют на твердое тело.

Одним из основных понятий в статике, как и во всей механике, а то и во всех естественных науках, является понятие о силе.

Опыт показывает, что когда движение материальной точки в инерциальной системе отсчета, отклоняется от равномерного и прямолинейного, то эта точка находится под действием физических сил, которые ее окружают.

Величина, которая является мерой механического взаимодействия материальных тел, называется силой. Взаимодействие между телами может происходить при помощи непосредственного контакта между физическими телами и при помощи полей разной природы.

По наблюдениям, сила, действующая на тело, -вектор. Она характеризуется точкой приложения, направлением и величиной. В теоретической механике силу принято обозначать На рис. 1.1. -сила, — точка приложения силы, прямая -линия действия силы.

В Международной системе единиц за единицу силы берут один ньютон (1 Н), в технической системе единиц — одну килограмм силу (1 кг или 1 кгс), в системе СГС — одну дину (1 дин).

В системе СI основными являются единицы длины, массы и времени. За единицу длины взят один метр (1 м). Метр равен 1650763,73 длинны волны в вакууме излучения, что соответствует переходу между уровнями и атома криптона-86. Секунда равна 9192631770 периодам излучения соответствующего перехода между двумя сверхтонкими уровнями основного состояния атома цезия-133. За единицу массы берут один килограмм (1 кг), который равен массе международного прототипа килограмма.

Ньютон — это такая сила, которая массе в 1 кг придает ускорение в Одна дина численно равна силе, которая сообщает телу массой в 1 грамм ускорение в 1 см/с². Один килограмм-сила — это сила, которая придает массе в 1 кг ускорение, равное ускорению свободного падения или

Приведем некоторые понятия и определения, которые понадобятся в дальнейшем. Будем различать три типа векторов: фиксированные, которые физически приложенные к определенной точке пространства, скользящие, — которые можно перемещать вдоль некоторых прямых, свободные, которые физически не связаны с определенной точкой пространства.

Два скользящих вектора эквиваленты, если они одинаковые по величине, и направленные в одну сторону вдоль одной прямой.

Материальная точка находится в равновесии, если она находится в состоянии покоя, или равномерного прямолинейного движения.

Система материальных точек находится в равновесии, если все точки системы находятся в состоянии покоя, или двигаются равномерно, прямолинейно с одинаковой скоростью по величине и направлению.

Уравновешенной (или эквивалентной нулю) называется система сил, которая оставляет в равновесии материальную точку, на которую она действует.

Две системы сил эквивалентны, если они не нарушают состояния абсолютно твердого тела, и их можно преобразовать друг в друга.

Равнодействующая сила— сила, эквивалентная заданной системе сил обозначается

В основе статики лежит ограниченное количество истин, которые называются аксиомами, в которых отображаются свойства сил, действующих на тело, или систему тел. Эти свойства тел установлены экспериментами и численными наблюдениями.

В статике рассмотрим пять аксиом, которых достаточно, чтобы ее обосновать, — аксиомы про силы, связи и аксиому про затвердение.

Аксиома про две силы

Аксиома I (про две силы). Две силы, приложенные к абсолютно твердому телу, взаимно уравновешенные( эквивалентные нулю), тогда и только тогда, когда они одинаковые по величине и действуют вдоль одной прямой в противоположных направлениях (рис. 1.2).

(1.1)

Эта аксиома справедлива только для абсолютно твердого тела. В случае деформированного твердого тела она не всегда справедливая.

Аксиома II ( про параллелограмм сил). Равнодействующая двух сил, приложенных к телу в одной точке, равна векторной сумме этих сил (рис. 1.3) и приложенная в той самой точке.
Это можно записать так:
(1.2)

Модуль равнодействующей силы определяется по теореме косинусов.
(1.3)

направление равнодействующих двух сил определяется диагональю параллелограмма, построенного на этих силах, как на сторонах.

На основании аксиомы II прейдем к правилу многоугольника сил, по которому любое число сил, приложенных в одной точке, можно складывать геометрически. Равнодействующую сил (рис. 1.4) определим как векторную сумму этих сил. Для этого (рис.1.5) с конца вектора, который равен силе откладываем вектор, который равен силе и т.д. Соединяя начало первого вектора с концом второго вектора находим равнодействующую силу
(1.4)
Полученный таким образом многоугольник называется многоугольником сил, или силовым многоугольников.

На основании изложенного материала можно установить условия равновесия сил, приложенных в определенной точке. Действительно, пусть в точке А приложена сила уравновешенная системе сил (эквивалентная нулю) (рис. 1.6,а). Построив многоугольник сил (рис. 1.6,б), видим, что начало первого вектора и конец последнего совпадают. Следовательно, равнодействующая уравновешенной силы равна нулю:
(1.5)
Многоугольник этих сил оказался замкнутым. Последнее выражает условие уравновешенности сил, приложенных к точке, в графической форме.

Связи и их реакции. Аксиомы про связи

В теоретической механике различают свободные и несвободные системы материальных точек, и следовательно, свободные и несвободные твердые тела.

Система материальных точек называется свободной, если на движение этих точек не накладываются ограничения. В ином случае систему материальных точек называют несвободной. Тела или поля, ограничивающие свободу движения системы материальных точек или твердого тела, называются связями. Если система материальных точек, или тело несвободные, то считают, что на них наложенны связи.

В статике рассматриваются простейшие связи, осуществленные в форме различных твердых или гибких тел. Реакцией связи называется сила, с которой связь действует на систему материальных точек или твердое тело. В случае несвободной системы или твердого тела, силы делятся на активные и реакции связей. Активными называются силы, вызывающие своим действием ускорения точек системы или реакции связей. Активные силы не зависят от связей. Реакции связей называют также пассивными силами, потому что
они возникают лишь тогда, когда на тело действуют активные силы. Рассмотрим аксиомы о связях.

Аксиома III (про освобождение от связей). Не меняя механического состояния (движения или равновесия) системы материальных точек или твердого тела, связь, наложенную на систему или твердое тело, можно отбросить, заменив действие связи ее реакцией, приложенной к этому телу, или системы в точке взаимодействия тела и связи.

Следует отметить, что силы, с которыми рассматриваемые тела действуют на связи, не уравновешиваются реакциями связей, поскольку силы и реакции связей приложены к разным телам, хоть по третьему закону Ньютона они одинаковые по величине и противоположные по направлению. Действие приложено к телам, образующие связи;
противодействие (реакции связей) приложенное к телам, движение или равновесие которых изучается.

С этой аксиомы следует, что несвободные материальные точки, систему материальных точек, или твердое тело, можно рассматривать как свободные, если их освободить от связей, заменяя действие последних их реакциями.

Аксиома IV ( про наложение новых связей). Равновесие системы материальных точек или твердого тела не нарушится при наложении на них новых связей.

Например, если стол, который стоит на полу, находится в равновесии, то это равновесие не нарушается, если ножки стола прикрепленные к полу болтами.

Аксиома V (про затвердевание) . Если деформированное тело находится в равновесии, то
равновесие его нарушиться, если, не меняя его формы, размеров, положения в
пространстве, подать его в виде соответствующего абсолютно твердого тела.

Поскольку в этой аксиоме речь идет не о каком-то физическом затвердении, а о наложении на частицу тела новых связей, то ее следует рассматривать как частный случай аксиомы IV.
Аксиома о затвердевании позволит в дальнейшем решать простейшие задачи статики деформируемых тел (ременная передача, цепь, нить и т.п.), применяя к ним методы статики твердого тела.

Простейшие теоремы статики

Теорема (о силе как скользящем векторе). Действие силы на твердое тело не изменится, если перенести силу по линии ее действия в любую точку.
Доказательство. Пусть в точке А приложена к телу сила (рис. 1.7). Выберем на линии действия этой силы любую точку В и приложим к ней две уравновешенные силы и . На основости аксиомы I сила в точке А и сила в точке В взаимно уравновешиваются (система сил эквивалентная нулю). Остается сила приложенная в точку В, что и нужно было доказать.

С теоремы выплывает, что сила, приложенная к абсолютно твердому телу, является скользящим вектором.

Теорема (о трех силах). Если абсолютно твердое тело находится в равновесии под действием трех параллельных сил и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.

Доказательство. Пусть твердое тело находится в равновесии вод действием непараллельных сил (рис. 1.8), из которых и лежат в одной плоскости. Продолжим линию действия сил и и найдем их точку пересечения О, существование которой обеспечивается условием теоремы. Перенесем силы и вдоль их линий действия в точку О и найдем равнодействующую Заменив и из равнодействующей , получим новую систему сил , эквивалентную заданной , то есть . Но теперь можно предположить, что тело находится в равновесии под действием только двух сил и . Это возможно в виду аксиомы I, если и имеют общую линий действия. Следовательно, все три силы лежат в одной плоскости, и линия действия силы проходит через точку О. Теорема доказана.

Таким образом, для равновесия системы трех непараллельных сил, лежащих в одной плоскости, необходимо (но не достаточно), чтобы линии этих двух сил пересекались в одной точке.

Виды связей и их реакции

Рассмотрим виды связей, что чаще всего случаются при решении задач, и обозначим, как определять направление реакций этих связей. Касаемо величин этих реакций, то их можно найти из условий равновесия, поскольку они зависят от активных сил.

1. Если связь является идеально гладкой поверхностью, то точка контакта тела А с этой поверхностью может свободно скользить по ней. Поэтому реакция идеально гладкой поверхности направлена по нормали от поверхности. Эта реакция обозначается через или (рис. 1.9).

2. Если связь осуществляется нитью, веревкой или аналогичными телами (шнуром, тросом, цепью), то для упрощения постановки задач теоретической механики допускают, что нить является невесомой, гибкой и нерастяжимой. Реакция нити направлена вдоль нити к точке ее крепления и обозначается через . Например, если тело (рис. 1.10) подвешенное к потолку с помощью нитки , то реакция нитки направленная вдоль нитки к ее точке крепления

3. Если связью является шероховатая поверхность, то ее реакция раскладывается на две составляющие: — нормальную и — касательную (рис. 1.11), соответственно направлены по нормали и по касательной к поверхности. В этом случае касательная составляющая реакции является силой трения. Простейшие свойства трения изложены в следующем параграфе.

4. Связи могут быть выполнены в виде шарниров цилиндрических и сферических (рис. 1.12). Направления реакций таких связей заранее определить нельзя. Так, в случае цилиндрического шарнира (подшипника) (рис. 1.12, а) реакция его размещена будет в плоскости, перпендикулярной к его оси . Неизвестный вектор реакции связи в плоскости определяется двумя составляющими и по осям и , величины которых находят из условий равновесия. Направление реакции сферического шарнира (Рис. 1.12, б) или подпятника раскладывают по направлению трех взаимно перпендикулярных осей Модули и их направления определяют из условий равновесия соответствующих систем сил. В частном случае, когда можно пренебречь размерами шарниров и силами трения, возникающими в них, шарниры называют идеально точечными.

5. Связь может осуществляться в форме идеальных стержней. Весом таких стержней пренебрегают и считают, что на их концах есть точечные шарниры. Реакция такого идеального стержня направлена вдоль оси стержня, в чем нетрудно убедиться. Действительно, если пренебречь весом стержня, на концах которого точечные шарниры, то согласно аксиоме I, стержень находится в равновесии под действием двух сил приложенных к шарнирам (рис. 1.13). Эти силы равные по величине, действуют по прямой, которая соединяет шарниры, и направлены в противоположные стороны, то есть реакция идеального стержня также направляется вдоль оси стержня.

6. Связь может осуществляться в форме катков (подвижных шарниров) (рис. 1.14). Реакция катка направлена ​​перпендикулярно опорной плоскости катка.

Трение и скольжение

Предположение о идеально гладкой поверхности, примененное нами в п.1.6, противоречит эксперименту. Действительно, прикосновение двух тел происходит не в одной только точке. Оба тела испытывают при этом малые деформации, в следствии которых они касаются по определенной поверхности. Эксперимент убеждает в том, что кроме нормальной составляющей реакции возникает еще касательная, которая называется силой трения скольжения (рис. 1.15).

Различают трения покоя, или статическое трение, которое происходит при относительном покое соприкасающихся тел, и трения движения, что происходит при относительном движении этих тел. Приближенные законы трения скольжения или трения первого рода установили Г. Амонтон (1663-1705) и Ш. Кулон (1736-1806). Эти законы соответствуют простым опытам на основании которых они установлены. В теоретической механике трением скольжения интересуются только в связи с определением реакций связей.

Простейшие свойства трения можно установить, пользуясь простым прибором. который называется трибометр. Прибор состоит из стола, по которому движется тело весом (см. рис. 1.15). Это тело приводиться в движение с помощью нити, перекинутой через неподвижный блок , к концу которой подвешен груз весом Пусть в начальный момент тело находилось в покое, если постепенно увеличивать силу , то тело все равно будет в покое. Итак, горизонтальная составляющая реакции стола уравновешивает приложенную силу и растет вместе с ней до тех пор, пока равновесие не нарушится. Это произойдет тогда, когда сила трения достигнет своего максимального значения Опыты показали, что максимальное знания силы трения пропорционально нормальной реакции поверхности тела:

(1.6)

Коэффициент пропорциональности называется коэффициентом трения скольжения и определяется опытным путем, значение его для различных материалов приведены в справочниках. В табл. 1.1 для сравнения приведены коэффициенты сухого трения, и смазанных поверхностей некоторых материалов. Следует отметить, что эти данные дают приблизительную оценку коэффициентов трения и поэтому пригодны только для грубых подсчетов. В других случаях приходится проводить специальные опыты.

Механизм трения является достаточно сложным физическим процессом. Как показывают опыты, коэффициент трения первого рода является постоянной величиной только в ограниченном диапазоне скоростей, относительного движения, и сил сжатия поверхностей тел. При увеличении относительной скорости движения тел, коэффициент трения сначала уменьшается, а затем начинает расти. В некоторых аномальных случаях трения движения может быть не меньше чем трения покоя (например, материалы с высокой упругостью — резина и т.д.).

Коэффициенты сухого трения и смазанных поверхностей некоторых материалом.

Когда сила трения достигнет значения , наступит состояние предельного равновесия. Достаточно незначительного прироста силы чтобы тело сдвинулось с места. Как только тело начнет двигаться, сила трения сразу уменьшится. Многочисленные опыты показали, что почти всегда трение при взаимном движении тел несколько меньше
чем трение при взаимном покое: (Знак равенства соответствует предельному равновесию). Важно отметить, что сила трения всегда направлена ​​в сторону, противоположную направлению относительной скорости движения тел. Коэффициент трения зависит от материала соприкасающихся поверхностей, чистоты обработки их,
физического состояния. Он не зависит от площади соприкасающихся поверхностей тел.
Заметим, что когда тело находится на горизонтальной плоскости (рис. 1.16), то значение нормальной составляющей реакции равно весу тела Если тело находится на наклонной плоскости (рис. 1.17), то . Изложены вопросы о трения скольжения касаются только сухого трения. Если есть масло, то существуют свои законы трения. Основоположником теории трения при наличии масла является русский ученый Н. П. Петров. Дальнейшее развитие эта теория получила в трудах Н. Е. Жуковского и других исследователей. В зависимости от взаимных движений, трение между твердыми телами бывает трех видов:
1) трения скольжения, соответствует поступательному движению соприкасающихся тел друг относительно друга;
2) трения качения (например, колеса по рейке)
3) трения кручения (например, в подпятнике), имеющее по своей природе много
общего с трением скольжения.

Отметим, что при трении происходит рассеивания энергии, то есть превращение механической энергии в тепловую, поэтому в узлах с трением температура тел повышается. Рассмотрим равновесие тела при наличии трения скольжения. Предположим, что сила приложена под углом к нормали, проведенной к поверхности соприкасающихся тел (рис. 1.18, а). Тогда ее можно разложить на две составляющие: и одна из которых пытается сдвинуть тело с места, а вторая — прижать к плоскости. В случае граничного равновесия В тоже время а поскольку то . Отсюда выплывает, что

(1.7)

Очевидно, что направление активной силы (рис. 1.18, в) по любой (в общем случае параллельной) из образующих конуса с углом раскрытия , равного , будет соответствовать случаю предельного равновесия. Этот конус называется конусом трения.

Если угол наклона активной силы в нормали больше (рис. 1.18, б), то тело начнет двигаться, то есть потеряет равновесие, а если меньше , то тело всегда будет находиться в равновесии. Это свойство трения учитывается при формировании искусственных откосов, и имеет место в естественных откосах. Конусом трения объясняется явление заклинивания узлов машин, когда ни одной из приложенных внутри конуса сил, не удастся сдвинуть с места соответствующую деталь. Напоследок скажем несколько слов о роли трения в механических явлениях. Во многих случаях силы трения рассматривают как источники вредных сопротивлений движения машин или приборов. Однако в ряде других случаев, наоборот, без сил трения невозможен движение. Например, именно такая роль трения при ходьбе человека, движении всех видов колесных транспортных машин, прокатных установок. Во всех этих случаях движение невозможно по идеально гладкой поверхности. В динамике машин во многих случаях невозможно обеспечить их устойчивость движения, если в системе нет определенных сил рассеивания энергии, или сил сопротивления, которые имеют свойства трения.

Внешние и внутренние силы. Метод сечений

Кроме приведенной в п. 1.4 существует и другая классификация сил, которая применяется в теоретической механике.
Силы, приложенные к точкам системы, можно разделить на внешние и внутренние. Силы, действующие на точки системы, называются внешними, если они вызваны действием тел,
не входящих в систему. Внутренними называются силы взаимодействия между материальными точками одной и той же системы. Распределение сил на внешние и внутренние — условное. Если рассматривать систему Солнце — Земля, то силы, действующие на эту систему со стороны других тел Солнечной системы, например, со стороны Юпитера, являются внешними, а силы взаимодействия между Солнцем и Землей — внутренними. Если рассматривать систему Солнце — Земля — ​​Юпитер, то силы, с которыми Юпитер действует на Солнце и Землю, будут внутренними. Отсюда следует, что внутренние
силы этой системы материальных точек можно перевести во внешние относительно новой системы, которая является составной частью данной, которую можно получить в результате отсечения ее от этой системы. Метод «перевода» внутренних сил во внешние называется методом сечений. Этот метод является частным случаем применения аксиомы об освобождении от связей.

Поскольку внутренние силы в твердом теле уравновешиваются, то для их определения применяют метод сечений. Например, рассмотрим равновесие идеального стержня (Рис. 1.19), к точечным шарнирам которого приложенные силы и . Модули этих сил равны, а направления противоположны . Нужно определить силу взаимодействия частей стержня в некоторой точке , то есть . Эта сила внутренняя. Применив метод сечений, переведем эту силу во внешнюю. Проведя, в точке сечение, рассмотрим равновесие, например, части стержня и определим силу, с которой часть стержня действует на .

На основании аксиомы I равновесие под действием сил и возможно тогда, когда эти силы действуют вдоль одной прямой, равны по модулю и противоположны по направлению . Итак, силу , которая является усилием стержня в точке , мы определили.

Методические указания:
Начиная изучение статики, следует глубоко усвоить определение основных понятий и изучить аксиомы механики. Надо обратить внимание на то, что аксиома о двух силах устанавливает, под действием какого наименьшего количества сил возможно равновесие
твердого тела.
Аксиома о параллелограмме сил позволяет выполнить замену двух сил, приложенных в определенной точке твердого тела, силой, им эквивалентной, то есть равнодействующей.
Теорема о трех силах облегчает определение направлений тех реакций связей, которые заранее определить нельзя.

Применение аксиомы III при решении конкретных задач, в которых рассматриваются несвободные тела, дает возможность освободить их от связей и рассматривать их как свободные, но под действием не только активных сил, но и реакций связей. Чтобы лучше усвоить статику, следует приобрести навыки в составлении и разложении сил по правилу параллелограмма.

В заключение сформулируем две основные задачи статики твердого тела:
1) задача о приведении заданной системы сил к другой, в том числе простой, что ей эквивалентна;
2) задача о равновесии системы сил, приложенных к определенному телу.

Первая задача является основной, она имеет важное значение не только в статике, но и в динамике. Вторая задача возникает тогда, когда заранее известно, что равновесие есть и обеспечивается, например, связями, наложенными на тело. Тогда условия равновесия, установлению которых для различных систем посвящены следующие разделы, во многих случаях позволяют определить реакции связей или другие неизвестные величины, входящие в условия равновесия.

Для решения второй задачи рекомендуется следующая методика:

1. Прочитав условие задачи и выписав исходные данные, следует определить объект исследования, то есть то тело, равновесие которого надо рассмотреть.
2. Освободить объект исследования от связей, заменив их действие силами, равными реакциям связей, и рассматривать этот объект как свободное тело, которое находится под действием активных сил и реакций связей.
3. В зависимости от характера полученной системы сил применить соответствующие условия равновесия.

Пример 1.
К балке в точке приложена сила опорами балки являются шарнир и каток . Длина балки Определите направление реакции шарнира и реакции и

Решение.
Следуя методических указаний, за тело, равновесие которого рассматривать, возьмем балку . Согласно аксиомы III заменим связи (шарнир и каток ) их реакциями. В соответствии с п.1.6, п. 6, реакция катка направлена ​​перпендикулярно к его опорной плоскости. Направление реакции шарнира заранее неизвестен. Однако балка находится в равновесии под действием трех непараллельных сил, линии действия которых по теореме о трех силы пересекаются в точке О (рис. 1.20, а). Следовательно, реакция шарнира направлена ​​по прямой . Построив замкнутый силовой треугольник (рис. 1.20, б), найдем направление реакции шарнира . Построение начинаем с известного вектора, который равен силе . Затем с конца этого вектора проводим прямую , параллельную , а с начала вектора С конца этого вектора проводим прямую параллельную . Итак, определим направление реакции шарнира. Наконец, из треугольника найдем его стороны, то есть величины и

Ответ:

Система сходящихся сил. Способы определения равнодействующей системы сходящихся сил

Системой сходящихся сил называется система таких сил, линии действия которых пересекаются в одной точке. Пусть задано произвольную систему сходящихся сил приложенных к твердому телу (см. рис. 1.4, 1.6, а). Перенесем эти силы, как скользящие вектора, в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействующую этих сил. Равнодействующую такой
системы сил можно определить графически и аналитически.

Графически равнодействующая сила определяется как замыкающая сторона многоугольника сил (См. рис. 1.5):

(1.8)

Аналитически равнодействующую силу можно определить по ее проекциями на оси
прямоугольной системы координат (рис. 1.21). Здесь и далее применяем правую систему
координат. По теореме о проекции векторной (геометрической) суммы на оси координат
получим:

(1.9)

где проекции соответствующих сил на оси координат.

Представим равнодействующую в виде разложения по ортам:
(1.10)

Тогда ее модуль запишем в виде:

(1.11)
или

(1.12)

Направление равнодействующей сил определяется такими направляющими косинусами:

(1.13)

Условия равновесия системы сходящихся сил

Теорема. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равна нулю:

(1.14)

Условие (1.14) является геометрическим условием равновесия системы сходящихся сил. Необходимость условия равновесия следует из того, что, заданная система сходящихся сил, приложенных к абсолютно твердому телу, эквивалентна одной силе — равнодействующей. Очевидно, что под действием одной силы тело будет находиться в равновесии только тогда, когда эта сила равна нулю, что следует из аксиомы о двух силы.

Докажем достаточность этого условия. Для этого покажем, что когда равнодействующая сила равна нулю, то система сходящихся сил находится в равновесии. Заданная система сил эквивалентна равнодействующей, равной нулю. Из определения уравновешенной (эквивалентной нулю) системы сил, ее можно отбросить, не нарушая состояния системы. Тогда на тело не действуют никакие силы и оно по первому закону Ньютона находится в равновесии.
Поскольку то многоугольник сил должен быть замкнутым, то есть конец последней силы совпадает с началом первой силы (рис. 1.22), выражающей условие равновесия системы сходящихся сил в графической форме (им удобно пользоваться в случае плоской системы сил).

Векторному равенству (1.14) соответствуют три скалярные равенства:
которые, с учетом формул (1.9), перепишем в виде:

(1.15)

Условия (1.15) являются условиями равновесия системы сходящихся сил в аналитической форме и формулируются так: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций сил на три взаимно перпендикулярные оси были равны нулю. В случае равновесия системы сходящихся сил,
лежащие в одной плоскости, например получим:

(1.16)

Итак, для равновесия системы сходящихся сил, лежащих в плоскости, необходимо и достаточно, чтобы алгебраические суммы проекций этих сил на две взаимно перпендикулярные оси были равны нулю.
Условия равновесия (1.15) и (1.16) называются также уравнениями равновесия. Из них
определяются неизвестные величины при решении конкретных задач. Если неизвестными силами являются реакции связей, то их количество не должно превышать числа уравнений равновесия, иначе задача будет статически неопределенной и решить ее методами теоретической механики не удастся.

Пример 2. Однородный шар радиусом и весом касается в точке к гладкой вертикальной стенке (рис. 1.23, а) содержится в равновесии веревкой длиной 0,8 м. Определить натяжение веревки и давление шара на стенку, если расстояние от точки к вертикали равна 0,4 м.
Решение.
Поскольку известна сила приложенная к шару, то рассмотрим равновесие шара. Связями для шара является стенка и веревка . Поскольку стенка гладкая, то реакция будет перпендикулярна к стенке; реакция веревки направлена ​​по ней. Поскольку силы , и удовлетворяют теорему о трех силах, то для равновесия шара необходимо и достаточно, чтобы силовой треугольник, или треугольник сил, был замкнут (рис. 1.23, б). Как видно из рис. 1.23, 6, силовой треугольник — прямоугольный. Угол между и обозначим через .
Получим

Из треугольника :

Тогда

Следовательно,

Предмет статики — основные понятия и определения

Вспомним основные понятия теоретической механики, которые хорошо известны из
курса физики.

Материальная точка — это тело определенной массы, размерами и формой которого можно пренебречь в условиях данной задачи.

Система материальных точек (материальная система) — это совокупность точек, положение и движение которых взаимосвязаны и взаимообусловлены.

Абсолютно твердое тело — это тело, в котором расстояния между двумя произвольными точками не изменяются со временем, проще, это тело, не деформируется под действием сил.

Вполне понятно, что в природе и технике не существует реальных тел, полностью соответствуют этим понятиям. Материальная точка, система материальных точек и твердое тело являются идеальными понятиями, расчетными моделями при изучении механики.

Задачи статики

Прежде, чем изучать первый раздел теоретической механики — статику, сформулируем задачи статики. Таковыми являются:

1) определение условий равновесия тел под действием различных систем сил как на плоскости, так и в пространстве;
2) определение методов преобразования систем сил с целью упрощения и замены их наименьшим количеством силовых факторов.

В основе этого раздела механики положены аксиомы статики, которые ниже будут рассмотрены. А теперь рассмотрим еще некоторые основные понятия статики и определения.

Сила — это количественная мера механического взаимодействия двух тел, которая определяет характер, величину и направление взаимодействия.

С этого классического определения силы следует, что она является величиной
векторной, а потому имеет три главных параметра: величина силы (или модуль), направление действия и точка приложения.

На расчетно–силовых схемах силу изображают в виде вектора произвольной длины (кроме случаев графической статики, когда силу чертят в масштабе). Покажем, например, (рис. 1.1) произвольную силу , которая изображена в виде вектора , приложенная в точке А и действует вдоль линии MN.

В Международной системе единиц измерения (СИ) единицей измерения силы один ньютон — [1 Н] или один килоньютон [1 кН].

Причем 1 [кН] = 1000 [кН]. В технической системе (МКГСС) единицей измерения силы является один килограмм-силы — [кГ] или [кгс], в системе (СГС) — одна дина [дин].

На тело могут одновременно действовать несколько сил, образуя систему.

Система сил — это совокупность нескольких сил, действующих на тело или на
механическую систему одновременно.

Эквивалентные системы сил — это такие системы сил, которые на одно и тоже
тело действуют одинаково. Система сил может быть, в некоторых случаях,
эквивалентна нулю.

Равнодействующая сила системы сил — это такая сила, действие которой эквивалентно действию заданной системы сил.

Уравновешивающая сила — это сила, которая по величине равна равнодействующей силе, расположенная с ней на одной прямой, но противоположна по направлению.

Аксиомы и определения статики

В основу статики положены аксиомы, то есть положения, которые принимаются без доказательства, так как они подтверждены многовековой практикой.

І аксиома. Абсолютно твердое тело под действием двух сил только тогда будет
находиться в равновесии, когда их векторы равны по модулю, противоположны по направлению и линии их действия совпадают.

На рис. 1.2 показано произвольное тело, которое находится в состоянии равновесия
под действием двух сил и , которые имеют одинаковые модули || = ||, расположенные на одной прямой MN и имеют противоположные направления. Точки приложения сил могут совпадать. Таким образом, = – .

ІІ аксиома. Состояние равновесия тела не нарушится, если к телу присоединить или отвергнуть уравновешенную систему сил. Например, система уравновешенных сил (, ) показана на рис. 1.2. Эта аксиома носит название аксиомы исключения сил.

Следствие из первых двух аксиом. Точку приложения силы можно передвигать в пределах данного тела вдоль линии действия силы (сила является скользящим вектором).

Предположим, что на тело (рис. 1.3) действует вектор силы , который приложен в точке А и имеет линию действия MN. Приложим в произвольной точке B на линии действия MN две силы и , такие, что = , а = – . Согласно первой аксиоме эти силы уравновешены, а согласно второй аксиоме их можно присоединить, не меняя кинематического состояния тела.

Но эту систему трех сил можно рассматривать по-другому: как силу , которая равна силе и перенесена из точки А в точку B, и уравновешенную систему двух сил ( и ), которую можно отбросить.

ІІІ аксиома. Равнодействующая двух не параллельных сил, которые приложенные к телу в одной точке, изображается диагональю параллелограмма, который построен на этих силах, как на сторонах, и приложенная в точке их сечения. Эта аксиома носит название закона параллелограмма сил.

Предположим, что к телу (рис. 1.4) в точке А приложены две силы и , которые расположены под углом α. Построим на этих силах, как на сторонах, параллелограмм и проведем через точку А диагональ, которая и будет равнодействующей этих сил.

Таким образом, III аксиома статики дает возможность геометрически добавить две силы, приложенные в одной точке

= +

Из курса геометрии известно, что диагональ параллелограмма, то есть модуль
равнодействующей, равно

Предлагается самостоятельно определить равнодействующую, если силы
приложенные в одной точке и расположены под прямым углом, а также когда они совпадают по направлению или направлены в противоположные стороны.

IV аксиома. Два взаимодействующих тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Эта аксиома носит название закона действия и противодействия.

Следует заметить, что силы взаимодействия никогда не уравновешиваются, потому
что они приложены к разным телам.

V аксиома. Если деформируемое (нетвердое) тело находится в состоянии равновесия под действием системы сил, то это состояние не изменится, если тело затвердеет. Эта аксиома называется принципом затвердевания.

Основные типы связей и их реакции

В теоретической механике твердые тела и материальные системы делятся на свободные и несвободные.

Тело считается свободным, если оно имеет возможность двигаться в пространстве в каком-либо направлении (или, если на движение системы не наложены ограничения).

Тело, движение которого в пространстве чем-то ограничивается, считается несвободным.

Тела, или препятствия, которые ограничивают движение данного тела, называются
связями. Если тело несвободно, то считают, что на его наложенные вязи.

Механическое воздействие вязи на это тело называется силой реакции вязи (в дальнейшем «реакция»).

В статике рассматриваются простейшие вязи в форме различных твердых и гибких тел.

Рассмотрим основные типы связей как расчетные модели. Каждая из этих связей имеет свое название, графическое изображение и свои реакции.

1. Идеально гладкая поверхность или опора (рис. 1.5, а). Реакция этой вязи направлена ​​перпендикулярно к поверхности, или расположена вдоль нормали. Гладкая плоскость накладывает одну вязь — невозможность двигаться по нормали от поверхности, поэтому будет одна реакция, которая направлена ​​против направления вторичного перемещения за счет наложения вязи.

Если поверхность является сферической (рис. 1.5, а 1), то реакция проходит через центры сфер О и О₁ по нормали n (перпендикулярно касательной ).

2. Точечная опора (рис. 1.5, б). Если гладкая плоскость вырождается в линию или точку, то реакция связей и будет направлена по перпендикуляру к линии (поверхности) тела, которое содержится в данной точке.

3. Шарнирно-неподвижная опора или неподвижный шарнир (подшипник) (рис. 1.5, в). Реакция шарнирно-неподвижной опоры приложена в центре шарнира и заранее неизвестна по направлению. Неизвестный вектор реакции разлагается на две составляющих вдоль осей координат и . С другой стороны, эта опора накладывает две вязи — невозможность вертикального и горизонтального перемещений, по-этому так и будет две соответствующие составляющие реакции в плоскости, перпендикулярной оси шарнира.

4. Шарнирно-подвижная опора или каток (рис. 1.5, г). Реакция этой вязи направлена ​​перпендикулярно к плоскости, в которой движется каток.

5. Жесткое закрепление (рис. 1.5, д). Реакция этой вязи должна быть представлена ​​двумя составляющими в виде сил и и реактивного момента M_R. Это соответствует количеству связей, которые накладывает эта опора: невозможность вертикального и горизонтального линейных перемещений и поворота в плоскости.

6. Идеальный стержень, то есть невесомый тонкий стержень, на концах которого установлены цилиндрические, точечные шарниры и который работает только на растяжение или на сжатие (рис. 1.5, е). Реакция этой вязи направлена ​​вдоль стержня и приложена в центре шарнира.

7. Гибкая нить или вязь, которая осуществляется идеальными гибкими телами, то есть невесомыми, нерастяжимой нити: канатами, ремнями, цепями (рис. 1.5, ж). Реакция этой вязи направлена ​​вдоль нити и приложена в точке закрепления А. В ременной передаче натяжения в ее ветвях и также считаются реакциями гибких связей.

8. Сферический шарнир или его частичный случай — подпятник (рис. 1.5, з, и). Реакция этой вязи должна быть изображенной тремя составляющими в виде реакций , , направленных вдоль осей пространственной декартовой системы координат x y z, с началом в центре сферического шарнира или подпятника.

В связи с введением понятия связей вводится VI и VII аксиомы статики, которые носят названия аксиомы об освобождении от связей и аксиомы о наложения новых связей.

VI аксиома. Равновесие заключенного материального тела не нарушится если отбросить вязи, что наложенные на него, а вместо них приложить силы, равные их реакциям.

VII аксиома. Равновесие заключенного материального тела не нарушится если на него наложить новые вязи.

Классификация систем сил

По характеру расположения все системы сил можно разделить на плоские и пространственные системы. Кроме того, каждая из этих систем может быть разделена на систему сходящихся сил, систему параллельных сил и систему произвольных сил.

Сделаем следующие определения:

— система сходящихся сил характеризуется тем, что направления векторов всех сил пересекаются в одной точке;

— в системе параллельных сил векторы сил параллельные;

— в системе произвольных сил векторы расположены как угодно на плоскости или в пространстве.

Таким образом, можно констатировать, что имеем шесть различных систем сил, под действием которых тело может находиться в состоянии равновесия, или двигаться по
определенному закону.

Услуги по теоретической механике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.