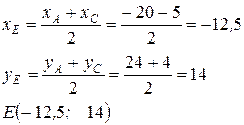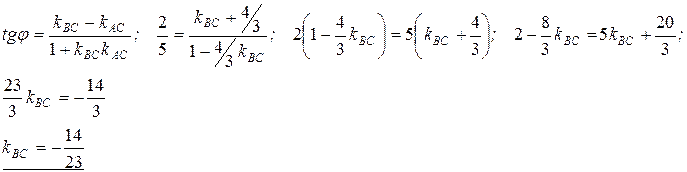Диагонали ромба
Свойства
Диагонали ромба обладают рядом особенностей, которые позволяют использовать их в вычислениях самих по себе. Во-первых, диагонали ромба пересекаются под прямым углом, что значит, что они образуют прямоугольные треугольники во внутреннем пространстве фигуры со стороной в качестве гипотенузы. Во-вторых, узнать длину катетов этих треугольников достаточно просто, так как точкой пересечения – вершиной прямого угла, диагонали делятся на две равные части. Подставив это в теорему Пифагора, можно найти сторону ромба как половину квадратного корня из произведения диагоналей. (рис.115.2) a=√(〖d_1〗^2+〖d_2〗^2 )/2
Угол напротив каждой диагонали можно найти из равнобедренных треугольников по теореме косинуса, заменив сторону ромба на полученный радикал. (рис.115.4) cosα=(〖2a〗^2-〖d_1〗^2)/〖2a〗^2 =((〖d_1〗^2+〖d_2〗^2)/2-〖d_1〗^2)/((〖d_1〗^2+〖d_2〗^2)/2)=(〖d_2〗^2-〖d_1〗^2)/(〖d_1〗^2+〖d_2〗^2 ) cosβ=(〖2a〗^2-〖d_2〗^2)/〖2a〗^2 =(〖d_1〗^2-〖d_2〗^2)/(〖d_1〗^2+〖d_2〗^2 )
Чтобы найти высоту ромба через диагонали, надо умножить выражение, соответствующее стороне на синус найденного угла, как отношение катета к гипотенузе в прямоугольном треугольнике. (рис.115.1) h=a sinα=sinα √(〖d_1〗^2+〖d_2〗^2 )/2
Периметр ромба будет равен радикалу стороны, умноженному на четыре (коэффициенты сокращаются, и остается два), а площадь – радикалу, возведенному в квадрат и умноженному на синус угла α. P=4a=2√(〖d_1〗^2+〖d_2〗^2 ) S=a^2 sinα=(sinα (〖d_1〗^2+〖d_2〗^2 ))/4
Радиус окружности, вписанной в ромб, представляет собой перпендикуляр стороны, проведенный к точке пересечения диагоналей, при продлении которой ровно в два раза получается высота ромба. Соответственно, чтобы найти радиус вписанной окружности через диагонали ромба, нужно разделить полученную формулу для высоты на два. (рис.115.3) r=h/2=sinα √(〖d_1〗^2+〖d_2〗^2 )/4
Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
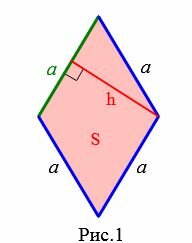 |
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| \(\small a=\frac<\large S><\large h>.\) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
| \(\small S=a \cdot h.\) |
Откуда легко вывести формулу (1).
2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
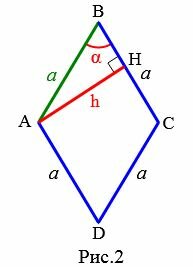 |
Для прямоугольного треугольника AHB применим теорему синусов:
| \(\small \frac<\large a><\large \sin 90°>=\frac<\large h><\large \sin \alpha>.\) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| \(\small a=\frac<\large h><\large \sin \alpha>.\) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: \(\small \angle C=180°-\alpha.\) Следовательно \(\small \sin \angle C=\sin(180°-\alpha)=\sin \alpha.\) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
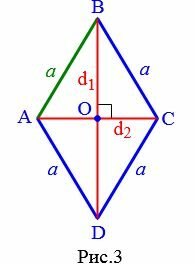 |
Применим к прямоугольному треугольнику AOB теорему Пифагора:
| \(\small a^2= \left( \frac<\large d_1> <\large 2>\right)^2+\left( \frac<\large d_2> <\large 2>\right)^2.\) |
| \(\small a= \frac<\sqrt<\large d_1^2+d_2^2>> <\large 2>\) | (3) |
4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
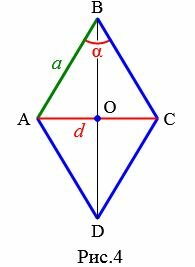 |
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
| \(\small \frac<\large a><\large \sin 90°>=\frac<\large \frac |
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sin \frac< \alpha>< 2>>.\) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| \(\small \sin \frac< \alpha>< 2>=\sqrt<\frac<\large 1-\cos \alpha><\large 2 >>.\) | (5) |
Подставляя (5) в (4), получим:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sqrt<\frac<\large 1-\cos \alpha><\large 2 >>>.\) |
| \(\small a=\large \frac< d>< \sqrt< 2-2 \ \cdot \ \cos \alpha>>.\) | (6) |
5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
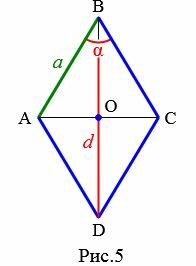 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| \(\small \frac<\large OB > <\large a>=\cos \angle ABO.\) | (7) |
Учитывая, что \( \small BO=\frac<\large d><\large 2>\) и \( \small \angle ABO=\frac<\large \alpha><\large 2>\), формулу (13) можно записать так:
| \(\small \frac< \large \frac<\large d > <\large 2>><\large a>= \cos \frac<\large \alpha> <\large 2>.\) |
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \cos \large \frac< \alpha>< 2>>.\) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| \(\small \cos \frac< \alpha>< 2>=\sqrt<\frac<\large 1+\cos \alpha><\large 2 >>.\) | (9) |
Подставляя (9) в (8), получим:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sqrt<\frac<\large 1+\cos \alpha><\large 2 >>>.\) |
| \(\small a=\large \frac< d>< \sqrt< 2+2 \ \cdot \ \cos \alpha>>.\) | (10) |
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| \(\small S= 2 \cdot a \cdot r.\) | (11) |
Из формулы (11) получим:
| \( \small a=\frac<\large S> <\large 2 \ \cdot \ r>\) | (12) |
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| \(\small S= a^2 \cdot \sin \alpha.\) | (13) |
Из формулы (13) найдем a:
| \( \small a=\frac<\large S> <\large \sin \alpha>\) | (14) |
Получили формулу сторон ромба через площадь и угол.
б) уравнения сторон AB, BC, CD и DA
Сделайте чертеж.
Решение.
1. Найдем уравнение прямой, на которой лежит AC – вторая диагональ квадрата. Вспомним, что уравнение любой невертикальной прямой может быть приведено к виду y=kx+b, где параметр k – угловой коэффициент этой прямой.
В силу свойства 1) диагоналей квадрата угловые коэффициенты kAC и kBD прямых AC и BD связаны соотношением:
Найдем угловой коэффициент kBD. Для этого выразим y через x из данного уравнения прямой BD:
Итак, 
Теперь уже легко найти уравнение прямой AC. Нам известны координаты её точки А и угловой коэффициента kAC. Используем уравнение прямой, проходящей через данную точку в данном направлении:

Подставим в это уравнение числовые данные нашей задачи: хА=-3, уА=2, kАС=3. Получим: 
2. С помощью свойства 2) диагоналей квадрата найдем координаты центра Е квадрата – точки пересечения его диагоналей.
Поскольку точка Е лежит на диагонали АС, её координаты удовлетворяют прямой АС; аналогично рассуждая, получим, что координаты точки Е должны одновременно удовлетворять и уравнению прямой BD. Таким образом, координаты точки Е должны удовлетворять системе из уравнений прямых АС и BD
(первое — уравнение прямой BD, второе – прямой АС). Далее, почленно вычитая первое уравнение из второго, получим:

Подставим найденное значение х в любое из уравнений системы, например, в первое. Найдем, что у=5.
Итак, мы нашли координаты точки Е, центра квадрата: 

3. Найдем длину отрезка АЕ – половину диагонали квадрата, а затем воспользуемся тем, что и остальные вершины квадрата находятся от его центра на таком же расстоянии (свойства 2) и 3) диагоналей), т.е. что все вершины квадрата лежат на окружности радиуса АЕ с центром в точке Е.
Подставив в правую часть этой формулы числовые значения координат точек А и Е, получим, что

Уравнение окружности радиуса АЕ с центром в точке Е записывается в виде:

Подставив в него числовые значения радиуса АЕ и координат центра Е, получим уравнение окружности, проходящей через все вершины квадрата:

Теперь с помощью простого рассуждения находим по очереди координаты всех вершин квадрата.
Точки А и С лежат на пересечении найденной нами окружности и прямой АС, это общие точки указанных окружности и прямой. Значит, координаты этих точек – решения системы уравнений окружности и прямой:

Координаты вершины А мы знаем, поэтому будем искать вершину С.
Подставим во второе уравнение системы вместо у его выражение 3х+11 из первого уравнения. Получим:

откуда 







Во втором случае мы получили известную нам абсциссу вершины А (а из первого уравнения системы получим ординату этой вершины), а первый случай дает нам абсциссу вершины С: 
Аналогично, для нахождения координат вершин B и D надо решить систему, состоящую из уравнений прямой BD и той же окружности:

Итак, получены два решения системы, пара (1; 4) и (-5; 6). Одно из этих решений – координаты точки B, а второе – точки D. Поскольку обе эти вершины совершенно равноправны, мы можем любую из них обозначить буквой B, тогда вторая будет вершиной D. Вся разница в том, идут ли вершины A, B, C и D в порядке обхода контура квадрата по или против часовой стрелки, что для решения нашей задачи безразлично; просто надо выбрать одно из этих направлений произвольно.
Мы будем считать, что вершины квадрата таковы: B(1; 4); D(-5; 6).
4. Нам осталось найти уравнения сторон квадрата. Для этого вспомним уравнение прямой, проходящей через точки 


и подставим в него координаты соответствующих вершин квадрата.
Уравнение прямой AB получим, если в формулу (2) вместо точек M и N возьмем точки A и B:

Подставляя в это уравнение координаты вершин А(-3; 2) и B(1; 4), находим:
откуда 
Аналогично получаем уравнения других сторон. Теперь можно сделать чертеж – Рис. 1.
Задача 3
В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба. Сделать чертёж. А(-20; 24); С(-5; 4); tgC= 20 /21.
Изобразим графически положение ромба в прямоугольной системе координат Оху:
1) Запишем уравнение диагонали АС как уравнение прямой, проходящей через две заданные точки:
2) Так как в ромбе его диагонали взаимно перпендикулярны, то угловой коэффициент диагонали BD будет равен:
Определим координаты точки пересечения диагоналей ромба Е. Итак, Е – середина АС.
Запишем уравнение диагонали BD как уравнение прямой, проходящей через заданную точку Е в направлении, определяемом угловым коэффициентом.
3) Чтобы найти уравнения сторон ромба надо определить угловые коэффициенты kAB=kCD и kBС=kАD прямых на которых эти стороны лежат. Так как диагонали ромба делят его углы пополам, то положив С=2φ из формулы

Итак, tgφ=-2,5 – не удовлетворяет условию задачи, что угол φ – острый, поэтому tgφ=0,4.
· угол φ является углом между прямыми ВС и АС, то есть:
· угол φ является углом между прямыми DС и АС, то есть:
Так как противоположные стороны ромба параллельны, то определим угловые коэффициенты всех его сторон:
4) Вершины ромба В и D являются точками пересечения его соответствующих сторон АВ и ВС; СD и АD. Решим системы уравнений этих сторон.


Задача 1
Пусть точка А(-7; 3) — вершина квадрата ABCD, а его диагональ BD расположена на прямой 2х+у+6=0. Найдите:
в) координаты вершин B, C и D;
г) уравнения сторон AB, BC, CD и DA.
Задача 2
В ромбе ABCD известны координаты вершин А и С и тангенс внутреннего угла С. Найти уравнения диагоналей и сторон, координаты двух других вершин, а также площадь этого ромба. Сделать чертёж. А(5; 6); С(21; 18); tgC= 4 /3.
Задача 3
Даны координаты вершин треугольника АВС. Написать уравнения окружностей вписанной и описанной около данного треугольника. А(11; 5); В(5; -3); С(-4; -3).
http://matworld.ru/geometry/storona-romba.php
http://lektsii.org/6-85864.html