§ 1.28. Угловая скорость и угловое ускорение
Угловая скорость
Проведем координатную ось X через центр окружности (начало координат), вдоль которой движется точка (рис. 1.86). Тогда положение точки А на окружности в любой момент времени однозначно определяется углом φ между осью X и радиусом-вектором 
При движении точки угол φ изменяется. Обозначим изменение угла за время Δt через Δφ. Для нахождения положения точки в любой момент времени надо знать угол φ0 в начальный момент времени t0 и определить, на сколько изменился угол за время движения (рис. 1.87):
Пусть точка движется по окружности с постоянной по модулю скоростью. Тогда за любые равные промежутки времени радиус-вектор поворачивается на одинаковые углы. Быстрота обращения точки определяется углом поворота радиуса-вектора за данный интервал времени. Например, если радиус-вектор точки за каждую секунду поворачивается на угол 90° = 

Если при равномерном обращении за время Δt радиус-вектор повернулся на угол Δφ, то быстрота обращения определится углом поворота в единицу времени. Быстроту обращения характеризуют угловой скоростью.
Угловой скоростью при равномерном движении точки по окружности называется отношение угла Δφ поворота радиуса-вектора к промежутку времени Δt, за который этот поворот произошел.
Обозначим угловую скорость греческой буквой ω (омега). Тогда по определению(2)
В СИ(3) угловая скорость выражается в радианах в секунду (рад/с).
Радиан в секунду равен угловой скорости равномерно обращающейся точки, при которой за время 1 с радиус-вектор этой точки поворачивается на угол 1 рад.
Например, угловая скорость точки земной поверхности равна 0,0000727 рад/с, а точильного диска более 100 рад/с.
Угловую скорость можно выразить через частоту обращения, т. е. число оборотов за 1с. Если точка делает п оборотов в секунду, то время одного оборота равно 
Это время называют периодом обращенияи обозначают буквой Т. Таким образом, частота и период обращения связаны следующим соотношением:
T = 
Полному обороту точки на окружности соответствует угол Δφ = 2π. Поэтому, согласно формуле (1.28.2),
Частота обращения точек рабочих колес мощных гидротурбин составляет 1—10 с -1 , винта вертолета — 4—6 с -1 , ротора газовой турбины — 200—300 с -1 .
Если при равномерном обращении точки угловая скорость известна, то можно найти изменение угла поворота Δφ за время Δt. Оно равно Δφ = ωΔt. С учетом этого формула (1.28.1) примет вид: φ = φ0 + ωΔt. Приняв начальный момент времени t0 равным нулю, получим, что Δt = t — t0 = t. Тогда угол поворота равен
По этой формуле можно найти положение точки на окружности в любой момент времени.
Угловое ускорение
В случае переменной угловой скорости вводится новая физическая величина, характеризующая быстроту ее изменения, — угловое ускорение:
Угловое ускорение равно производной угловой скорости по времени. Если β = const, то ω(t) = ω0 + β(t — t0), где ω0 — угловая скорость в начальный момент времени t0. При t0 = 0
Эта формула подобна формуле проекции скорости vx = v0x + axt при прямолинейном движении точки. Соответственно угол поворота
Эту формулу можно получить точно таким же способом, как и уравнение координаты при прямолинейном движении х =
Связь между линейной и угловой скоростями
Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. Между линейной скоростью точки, обращающейся по окружности, и ее угловой скоростью существует связь. При равномерном движении точки по любой траектории модуль скорости равен отношению пути s ко времени Δt, за которое этот путь пройден. Точка А, движущаяся по окружноcти радиусом R, за время Δt проходит путь, равный длине дуги 

Итак, модуль линейной скорости точки, движущейся по окружности, равен произведению угловой скорости на радиус окружности:
Эта формула справедлива как для равномерного, так и для неравномерного движения точки по окружности.
Из выражения (1.28.9) видно, что чем больше радиус окружности, тем больше линейная скорость точки. Для точек земного экватора v = 463 м/с, а на широте Санкт-Петербурга — 233 м/с. На полюсах Земли v = 0.
Модуль ускорения точки, движущейся равномерно по окружности (центростремительное, или нормальное, ускорение) можно выразить через угловую скорость тела и радиус окружности. Так как а = 
Чем больше радиус окружности, тем большее по модулю ускорение имеет точка при заданной угловой скорости. Ускорение любой точки поверхности Земли на экваторе составляет 3,4 см/с 2 .
Связь линейного ускорения с угловым
С изменением угловой скорости точки меняется и ее линейная скорость. Нормальное ускорение связано согласно формуле (1.28.10) с угловой скоростью и не зависит, следовательно, от углового ускорения. Но тангенциальное ускорение, определяемое формулой (1.27.4), выражается через угловое ускорение:
Мы научились полностью описывать движение точки по окружности. При фиксированном радиусе окружности модуль скорости (линейная скорость) пропорционален угловой скорости, а нормальное ускорение пропорционально ее квадрату. Тангенциальное ускорение пропорционально угловому ускорению.
Упражнение 5
- Поезд движется по закруглению радиусом 200 м со скоростью 36 км/ч. Найдите модуль нормального ускорения.
- Тело брошено с поверхности Земли под углом 60° к горизонту. Модуль начальной скорости равен 20 м/с. Чему равен радиус кривизны траектории в точке максимального подъема?
- Определите радиус кривизны траектории снаряда в момент вылета из орудия, если модуль скорости снаряда равен 1 км/с, а скорость составляет угол 60° с горизонтом.
- Снаряд вылетает из орудия под углом 45° к горизонту. Чему равна дальность полета снаряда, если радиус кривизны траектории в точке максимального подъема равен 15 км?
- Сферический резервуар, стоящий на земле, имеет радиус R. При какой наименьшей скорости камень, брошенный с поверхности Земли, может перелететь через резервуар, коснувшись его вершины? Под каким углом к горизонту должен быть при этом брошен камень?
- Въезд на один из самых высоких в Японии мостов имеет форму винтовой линии, обвивающей цилиндр радиусом r. Полотно дороги составляет угол α с горизонтальной плоскостью. Найдите модуль ускорения автомобиля, движущегося по въезду с постоянной по модулю скоростью v.
- Точка начинает двигаться равноускоренно по окружности радиусом 1 м и за 10 с проходит путь 50 м. Чему равно нормальное ускорение точки через 5 с после начала движения?
- Поезд въезжает на закругленный участок пути с начальной скоростью 54 км/ч и проходит путь 600 м за 30 с. Радиус закругления равен 1 км. Определите модуль скорости и полное ускорение поезда в конце этого пути, считая тангенциальное ускорение постоянным по модулю.
- Груз Р начинает опускаться с постоянным ускорением а = 2 м/с 2 и приводит в движение ступенчатый шкив радиусами г = 0,25 м и R = 0,50 м (рис. 1.89). Какое ускорение а1, будет иметь точка М через t = 0,50 с после начала движения?
Рис. 1.89
- Маховик приобрел начальную угловую скорость ω = 2π рад/с. Сделав 10 оборотов, он вследствие трения в подшипниках остановился. Найдите угловое ускорение маховика, считая его постоянным.
- Маховое колесо радиусом R = 1 м начинает движение из состояния покоя равноускоренно. Через t1 = 10 с точка, лежащая на его ободе, приобретает скорость v1 = 100 м/с. Найдите скорость, а также нормальное, касательное и полное ускорения этой точки в момент времени t2 = 15 с.
- Шкив радиусом R = 20 см начинает вращаться с угловым ускорением β = 3 рад/с2. Через какое время точка, лежащая на его ободе, будет иметь ускорение а = 75 см/с2?
- Точка начинает обращаться по окружности с постоянным ускорением β = 0,04 рад/с2. Через какое время вектор ее ускорения будет составлять с вектором скорости угол а = 45°?
(1) Напомним, что радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности. 1 рад приблизительно равен 57°17’48». В радианной мере угол равен отношению длины дуги окружности к ее радиусу: 
(2) Когда точка движется неравномерно, то мгновенная угловая скорость определяется как предел отношения Δφ к Δt при условии, что Δt —> 0:
(3) СИ — Международная система единиц. В этой системе за единицу длины принят 1 м, за единицу времени — 1с. Подробнее о СИ будет рассказано в дальнейшем.
КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА
Краткая теория
Положение материальной точки или твердого тела при заданной оси вращения определяется углом поворота 


Средняя угловая скорость и среднее угловое ускорение материальной точки


где 

Мгновенная угловая скорость материальной точки

Мгновенное угловое ускорение

Направление векторов угловой скорости и углового ускорения совпадают с осью вращения (рис.2.1). Угловая скорость, угловое ускорение, как и угловое перемещение, являются псевдовекторами.
Частота вращения


где 
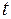
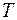
Число оборотов N, совершаемых телом при вращательном движении, связано с углом поворота φ соотношением:
УРАВНЕНИЯ ОСНОВНЫХ ВИДОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Кинематическое уравнение равномерного вращательного движения

где 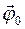
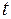
Кинематическое уравнение равнопеременного вращательного движения ( 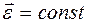

где 
Угловая скорость тела при равнопеременном вращательном движении
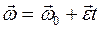
СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ, ХАРАКТЕРИЗУЮЩИМИ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Длина пути, пройденного материальной точкой по дуге окружности радиусом 

Связь между линейной и угловой скоростью(рис.2.2)


Связь между тангенциальным и угловым ускорением(рис.2.2)


Связь между нормальным ускорением и угловой скоростью


| КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ | КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ |
 |  |
  |   |
  |   |
 |  |
 |  |
 , при , при 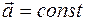 | 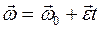 , при , при 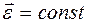 |
 , при , при  | 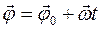 , при , при  |
 , при , при 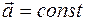 |  , при , при 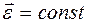 |
Вопросы для самоподготовки
1. Сформулируйте определение вращательного движения твердого тела.
2. Назовите основные кинематические характеристики вращательного движения, дайте им определение.
3. Объясните, почему линейное перемещение, скорость и ускорение не являются характеристиками вращательного движения твердого тела.
4. Дайте определение периода и частоты вращения.
5. Выведите кинематические уравнения равномерного и равнопеременного вращательного движения.
6. Выведите уравнение угловой скорости при равнопеременном вращательном движении.
7. Назовите формулы связи кинематических характеристик поступательного и вращательного движения.
8. Покажите аналогию между основными характеристиками поступательного и вращательного движения.
9. Материальная точка М движется по окружности со скоростью 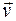

 |
Примеры решения задач
2.1.Материальная точка начинает двигаться по окружности радиуса r=10 см с постоянным касательным ускорением aτ=0,4 см/с 2 . Найти:
1) момент времени t от начала вращения, при котором вектор полного ускорения 
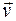
2) путь, пройденный материальной точкой за это время;
3) угол поворота материальной точки по окружности за это время.
1. По условию задачи материальная точка движется по окружности с постоянным касательным ускорением 

Скорость v и нормальное ускорение an=v 2 /r непрерывно возрастают со временем, а вектор полного ускорения 
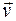


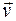
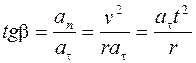
Тогда искомый момент времени найдем из соотношения:
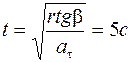
2. В соответствии с формулой (1.22) путь, пройденный материальной точкой за это время

3. Угол поворота φ при вращательном движении линейно зависит от пройденного пути по формуле (2.9) и также изменяется со временем по квадратичному закону. Тогда угол поворота материальной точки в момент времени t=5c равен:
φ 
Ответ: 1. 

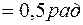
2.2. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением 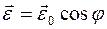

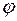
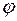
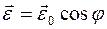

Выберем положительное направление оси z вдоль вектора 

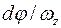

Проинтегрируем выражение (1) с учетом начального условия ( 




Ответ: 
2.3. Круглый конус с радиусом основания R и высотой h катится без скольжения по поверхности стола, как показано на рисунке 2.5. Вершина конуса закреплена шарнирно в точке О на уровне точки С – центра основания конуса. Точка С движется с постоянной скоростью v. Найти угловую скорость 
R, 
1. За промежуток времени dt цилиндр совершит поворот d 
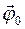


где 



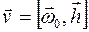
тогда 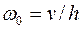

|
Их отношение 


Ответ: 
Движение по окружности
Движение по окружности — простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории — предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости — радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → — v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → — v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → — радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов — нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 — v 1 — изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
http://lektsii.org/3-85540.html
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/























