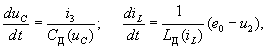Уравнения цепи через переменные состояния

№74 Расчет переходных процессов методом переменных состояния.

Уравнениями состояния электрической цепи называют любую систему дифференциальных уравнений, которая описывает состояние (режим) данной цепи. Например, система уравнений Кирхгофа является уравнениями состояния цепи, для которой она составлена.

В более узком смысле в математике уравнениями состояния называют систему дифференциальных уравнений 1-го порядка, разрешенных относительно производных (форма Коши). Система уравнений состояния в обобщенной форме имеет вид:

Та же система уравнений в матричной форме:

или в обобщённой матричной форме:

Система уравнений состояния формы Коши решается методом численного интегрирования (метод Эйлера или метод Рунге-Кутта) на ЭВМ по стандартной программе, которая должна быть в пакете стандартных программ. При отсутствии такой программы в пакете она легко может быть составлена по следующему алгоритму (метод Эйлера) для к-го шага:

Значения производных на к-ом шаге:

Значения переменных на к-ом шаге:

Для определения значений переменных и их производных на 1-м шаге ин¬тегрирова¬ния используются их значения на момент t=0, т.е. их начальные условия x1(0), x2(0). xn(0).

Уравнения состояния формы Коши для заданной схемы могут быть получены из системы уравнений Кирхгофа путем их преобразования. Для этой цели: а) из системы уравнений Кирхгофа методом подстановки исключаются »лишние» переменные, имеющие зависимые начальные условия, и оставляют переменные iL(t) и uC(t), которые не изменяются скачком и имеют независи-мые начальные условия iL(0) и uC(0); б) оставшиеся уравнения решаются относительно производных и приводятся их к форме Коши.

В случае сложных схем уравнения состояния формы Коши могут быть составлены топологическими методами с использованием матриц соединений [A] и [B].

Последовательность расчета переходного процесса методом переменных состояния выглядит так:

1. Производится расчет схемы в установившемся режиме до коммутации и определяются независимые начальные условия iL(0) и uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа для схемы после коммутации.

3. Методом исключения »лишних» переменных система уравнений Кирхгофа преобразуется в систему уравнений Коши, составляются матрицы коэффициентов.

4. Выбирается расчетное время (продолжительность переходного процесса) и число шагов интегрирования N.

5. Решение задачи выполняется на ЭВМ по стандартной программе. Выходную функцию получают в виде графической диаграммы x=f(t)или в виде таблицы координат функций для заданных моментов времени.

Пример. Для схемы рис. 74.1 с заданными параметрами элементов (e(t)=Emsin(ωt+ψE), R, R1, R2, R3, L1, L2, C) выполнить расчет переходного процесса и определить функцию uab(t).

1. Выполняется расчет схемы в установившемся режиме переменного тока до коммутации и определяются начальные условия i1(0), i2(0), uC(0).

2. Составляется система дифференциальных уравнений по законам Кирхгофа:

3. Система уравнений Кирхгофа преобразуется в систему уравнений Коши.

Для этой цели из (1) выражаем

и делаем подстановку в (1) и (2), а из (4) делаем подстановку в (1). Тогда получим:

Подсчитаем значения отднльных коэфициэнтов:

Составляем матрицы коэффициентов:

В качества исследуемого промежутка времени выбираем период переменного тока

Число шагов интегрирования принимаем N = 1000,

Вводим исходные данные в ЭВМ и выполняем рассчет.

В качестве выходной функции принимаем:

Для выходной функции Uab(T) строим графическую диаграмму в интервале периода Т.

Уравнения цепи через переменные состояния

Зная реакцию цепи на единичное возмущающее воздействие, т.е. функцию переходной проводимости или (и) переходную функцию по напряжению , можно найти реакцию цепи на воздействие произвольной формы. В основе метода – метода расчета с помощью интеграла Дюамеля – лежит принцип наложения.

При использовании интеграла Дюамеля для разделения переменной, по которой производится интегрирование, и переменной, определяющей момент времени, в который определяется ток в цепи, первую принято обозначать как , а вторую — как t.

Пусть в момент времени к цепи с нулевыми начальными условиями (пассивному двухполюснику ПД на рис. 1) подключается источник с напряжением произвольной формы. Для нахождения тока в цепи заменим исходную кривую ступенчатой (см. рис. 2), после чего с учетом, что цепь линейна, просуммируем токи от начального скачка напряжения и всех ступенек напряжения до момента t, вступающих в действие с запаздыванием по времени.

В момент времени t составляющая общего тока, определяемая начальным скачком напряжения , равна .

В момент времени имеет место скачок напряжения , который с учетом временного интервала от начала скачка до интересующего момента времени t обусловит составляющую тока .

Полный ток в момент времени t равен, очевидно, сумме всех составляющих тока от отдельных скачков напряжения с учетом , т.е.

.

Заменяя конечный интервал приращения времени на бесконечно малый, т.е. переходя от суммы к интегралу, запишем

.

(1)

Соотношение (1) называется интегралом Дюамеля.

Следует отметить, что с использованием интеграла Дюамеля можно определять также напряжение. При этом в (1) вместо переходной проводимости будет входить переходная функция по напряжению.

Последовательность расчета с использованием
интеграла Дюамеля

1. Определение функции (или ) для исследуемой цепи.
2. Запись выражения (или ) путем формальной замены t на .
3. Определение производной .
4. Подстановка найденных функций в (1) и интегрирование определенного интеграла.

В качестве примера использования интеграла Дюамеля определим ток в цепи рис. 3, рассчитанный в предыдущей лекции с использованием формулы включения.

Исходные данные для расчета: , , .

.

.

.

Полученный результат аналогичен выражению тока, определенному в предыдущей лекции на основе формулы включения.

Метод переменных состояния

Уравнения элекромагнитного состояния – это система уравнений, определяющих режим работы (состояние) электрической цепи.

Метод переменных состояния основывается на упорядоченном составлении и решении системы дифференциальных уравнений первого порядка, которые разрешены относительно производных, т.е. записаны в виде, наиболее удобном для применения численных методов интегрирования, реализуемых средствами вычислительной техники.

Количество переменных состояния, а следовательно, число уравнений состояния равно числу независимых накопителей энергии.

К уравнениям состояния выдвигаются два основных требования:

-возможность восстановления на основе переменных состояния (переменных, относительно которых записаны уравнения состояния) любых других переменных.

Первое требование удовлетворяется специальной методикой составления уравнений состояния, которая будет рассмотрена далее.

Для выполнения второго требования в качестве переменных состояния следует принять потокосцепления (токи в ветвях с индуктивными элементами) и заряды (напряжения) на конденсаторах. Действительно, зная закон изменения этих переменных во времени их всегда можно заменить источниками ЭДС и тока с известными параметрами. Остальная цепь оказывается резистивной, а следовательно, всегда рассчитывается при известных параметрах источников. Кроме того, начальные значения этих переменных относятся к независимым, т.е. в общем случае рассчитываются проще других.

При расчете методом переменных состояния, кроме самих уравнений состояния, связывающих первые производные и с самими переменными и и источниками внешних воздействий – ЭДС и тока, необходимо составить систему алгебраических уравнений, связывающих искомые величины с переменными состояния и источниками внешних воздействий.

Таким образом, полная система уравнений в матричной форме записи имеет вид

;

(2)

.

(3)

Здесь и — столбцовые матрицы соответственно переменных состояния и их первых производных по времени; — матрица-столбец источников внешних воздействий; — столбцовая матрица выходных (искомых) величин; — квадратная размерностью (где n – число переменных состояния) матрица параметров, называемая матрицей Якоби; — прямоугольная матрица связи между источниками и переменными состояния (количество строк равно n, а столбцов – числу источников m); — прямоугольная матрица связи переменных состояния с искомыми величинами (количество строк равно числу искомых величин к, а столбцов – n); — прямоугольная размерностью матрица связи входа с выходом.

Начальные условия для уравнения (2) задаются вектором начальных значений (0).

В качестве примера составления уравнений состояния рассмотрим цепь на рис. 4,а, в которой требуется определить токи и .

По законам Кирхгофа для данной цепи запишем

;

(4)

;

(5)

.

(6)

Поскольку с учетом соотношения (6) перепишем уравнения (4) и (5) в виде

или в матричной форме записи

Матричное уравнение вида (3) вытекает из соотношений (4) и (6):

Вектор начальных значений (0)= .

Непосредственное использование законов Кирхгофа при составлении уравнений состояния для сложных цепей может оказаться затруднительным. В этой связи используют специальную методику упорядоченного составления уравнений состояния.

Методика составления уравнений состояния

Эта методика включает в себя следующие основные этапы:

1. Составляется ориентированный граф схемы (см. рис. 4,б), на котором выделяется дерево, охватывающее все конденсаторы и источники напряжения (ЭДС). Резисторы включаются в дерево по необходимости: для охвата деревом всех узлов. В ветви связи включаются катушки индуктивности, источники тока и оставшиеся резисторы.

2. Осуществляется нумерация ветвей графа (и элементов в схеме), проводимая в следующей последовательности: первыми нумеруются участки графа (схемы) с конденсаторами, затем резисторами, включенными в дерево, следующими нумеруются ветви связи с резисторами и, наконец, ветви с индуктивными элементами (см. рис. 4,б).

3. Составляется таблица, описывающая соединение элементов в цепи. В первой строке таблицы (см. табл. 1) перечисляются емкостные и резистивные элементы дерева, а также источники напряжения (ЭДС). В первом столбце перечисляются резистивные и индуктивные элементы ветвей связи, а также источники тока.

Уравнения цепи через переменные состояния

29.3. УРАВНЕНИЯ СОСТОЯНИЯ НЕЛИНЕЙНЫХ ЦЕПЕЙ

Дифференциальные уравнения, описывающие динамические процессы в нелинейных цепях, имеют более широкое применение, чем в линейных цепях, так как они используются не только для расчетов переходных, но и периодических процессов. В связи с этим возникает необходимость выяснить, можно ли описывать нелинейные цепи с помощью переменных состояния, а также определить способы формирования уравнений состояния.

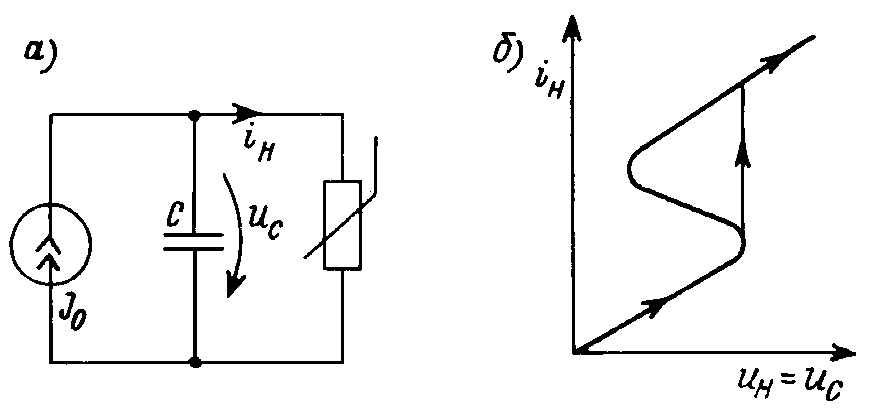
Переменные состояния. Напомним, что в линейной цепи переменные состояния i_L и u_C однозначно определяют токи и напряжения всех остальных ветвей. Нетрудно установить, что в нелинейной цепи с неоднозначными (немонотонными) характеристиками элементов такой однозначности может не быть. Рассмотрим в качестве примера простую цепь, состоящую из конденсатора с параллельно включенным нелинейным резистором (рис. 29.3, а ). Пусть нелинейный элемент имеет характеристику u_н(i_н), управляемую током (рис. 29.3, б ). Уравнение цепи J₀ = C du_C/dt + i_н содержит две переменные: u_C и ток нелинейного резистора i_н. Напряжение u_C нельзя принять за переменную состояния, так как оно не определяет однозначно ток i_н. Так как при заряде конденсатора наблюдается скачок тока i_н и его производная di_н/dt в момент скачка бесконечна, то использование переменной i_н в качестве переменной состояния также невозможно. Таким образом, динамические процессы в цепях с контурами из конденсаторов и управляемых током нелинейных резисторов нельзя описывать переменными состояния. Согласно принципу дуальности, аналогично в цепях, включающих сечения из катушек индуктивности и управляемых напряжением резисторов, также нельзя пользоваться уравнениями состояния. Простейшая такая цепь — это последовательное соединение катушки и резистора с N-образной характеристикой (например, туннельного диода). Для такой цепи характерны скачки напряжения при динамических процессах.

В связи с этим в дальнейшем будем рассматривать нелинейные цепи, в которых нет перечисленных особых контуров и сечений, и для их описания цепи можно использовать полную совокупность напряжений u_C (зарядов q_C) на конденсаторах и токов i_L (потокосцеплений Ψ _L) катушек цепи, через которые все остальные переменные выражаются однозначно.

Формирование уравнений состояния. В цепях, не имеющих отмеченных особенностей, в качестве переменных состояния могут выступать либо переменные u_C, i_L, либо входящие в уравнения цепи под знаком производных заряды нелинейных конденсаторов q_C и потокосцепления нелинейных индуктивностей Ψ _L. Выбор типа переменной — u_C или q_C и i_L или Ψ _L — для каждого элемента не имеет принципиального значения и обычно диктуется соображениями простоты записи уравнений, что определяется, в первую очередь, видом используемой аппроксимации характеристик. Например, при задании характеристики нелинейной катушки в форме i(Ψ) удобнее пользоваться в качестве переменной состояния потокосцеплением Ψ, и наоборот, если характеристика представлена в форме Ψ(i), разрешенной относительно тока, в качестве переменной состояния следует взять этот ток.

При использовании переменных u_C и i_L связи между токами и напряжениями на динамических элементах записываются в виде:

; .

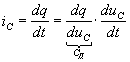
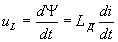
где C_Д — дифференциальная емкость; L_Д = d Y /di — дифференциальная индуктивность.

Уравнения Кирхгофа, являющиеся исходными для уравнений состояния нелинейной цепи, формируются так же, как в линейных цепях: используются главные сечения и главные контуры нормального дерева, включающего все конденсаторы и ни одной катушки (последние относятся к дополнению дерева).

Каждое из полученных уравнений первого и второго законов Кирхгофа закона содержит не более одной производной от переменной состояния по времени. Система включает также напряжения резистивных ветвей дерева и токи резистивных связей, которые необходимо выразить через переменные состояния. Для этого используют уравнения первого закона для главных сечений резистивных ветвей дерева и второго закона для главных контуров резистивных связей. Эти нелинейные, в общем случае, уравнения не содержат производных и служат основой для исключения избыточных переменных. Однако этот этап, как правило, требует решения нелинейной системы с помощью рассмотренных выше методов расчета нелинейных резистивных цепей (см. гл. 28).

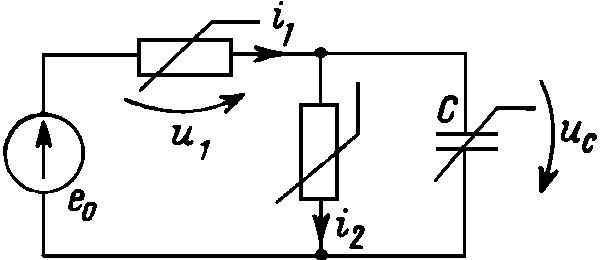Рис. 29.4

В качестве простейшего примера рассмотрим формирование уравнений состояния для цепи с одним конденсатором (рис. 29.4). Согласно сказанному выше, эта цепь описывается уравнениями состояния лишь в случае, если оба нелинейных резистора управляются напряжением и имеют характеристики i1(u1) и i2(u2).

Выбор нормального дерева здесь однозначен, и уравнение первого закона Кирхгофа для главного сечения, включающего конденсатор и нелинейные резисторы, записывают в виде:

Для главных контуров резистивных связей получим по второму закону:

Линейность этих уравнений позволяет исключить избыточные переменные i₁ и i₂ и свести систему к одному уравнению относительно переменной состояния u_C:

.

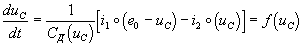
Здесь использовано то же символическое изображении функциональной зависимости i_°(u), что и в п. 28. 2.

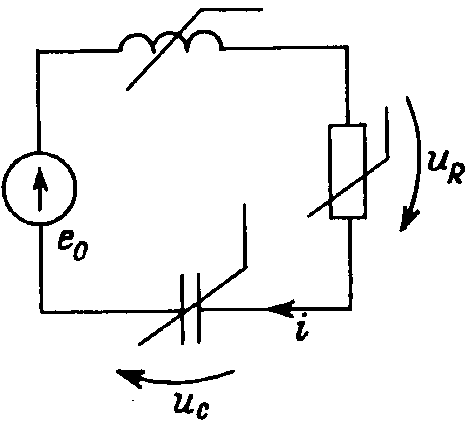
Рассмотрим далее формирование уравнений состояния нелинейного колебательного контура, находящегося под действием источника ЭДС (рис. 29.5). Так как резистивный элемент контура включен последовательно (образует сечение) с индуктивностью, уравнения состояния можно составить лишь в случае, если характеристика резистора управляется током и имеет вид u_R(i). Пусть характеристики элементов заданы в виде i(Ψ) — для катушки, q(u_C) — для конденсатора. Примем в качестве переменных состояния Ψ и u_C. Выбор нормального дерева здесь однозначен: оно включает элементы e₀, C и резистор.

Для главного сечения, включающего емкость, запишем dq/dt = C_Д du_C/dt = i(Ψ). Главный контур дает единственное уравнение второго закона Кирхгофа dΨ/dt = e₀ – u_R(i) – u_C. Перепишем оба уравнения в нормальной форме:

; .

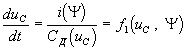
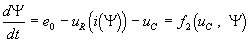
Таким образом, нам и в этом случае удалось правые части уравнений состояния f₁ и f₂ представить в виде, разрешенном относительно переменных состояния.

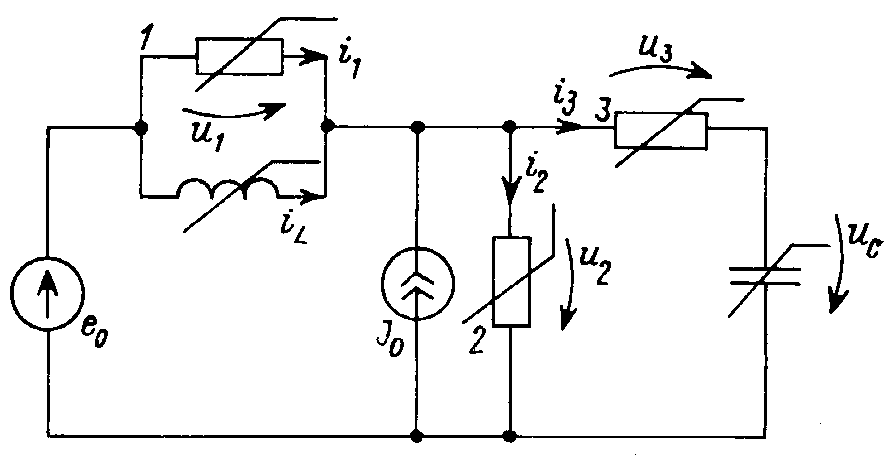
Однако, такая возможность существует не всегда. Покажем это на примере более сложной цепи, включающей нелинейные катушку и конденсатор и три резистивных элемента (рис. 29.6). Описать цепь с помощью переменных состояния i_L (или Ψ) и u_C (или q) можно при отсутствии особых контуров и сечений. Наличие контуров, включающих источник ЭДС, конденсатор и замыкающиеся через резисторы 1, 2; 2, 3 или 1, 3, показывает, что в цепи, описываемой уравнениями состояния, лишь один из резисторов может иметь характеристику, управляемую током. Так как элементы L, J₀ и все три резистора образуют сечение, то для искомого описания цепи необходимо, чтобы хотя бы один резистор управлялся током. Таким образом, рассматриваемая цепь допускает описание с помощью уравнений состояния лишь в случаях, когда один из резисторов цепи управляется током, а остальные два — напряжением. Рассмотрим вариант, в котором характеристики резисторов заданы в виде i₁(u₁), u₂(i₂), i₃(u₃).

.

При выборе в качестве ветвей дерева элементов e₀, R₂ и C (такой выбор не является однозначным) запишем для главных сечений по первому закону Кирхгофа:

; .

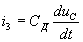
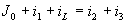
Применив второй закон Кирхгофа к главным контурам, получим

; ; .

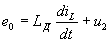
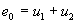
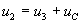
В этой системе избыточными переменными являются токи и напряжения всех резистивных элементов i₁, i₂, i₃, u₁, u₂, u₃. Для их выражения через переменные состояния имеем три алгебраических уравнения составленной системы и три связи между переменными резистивных ветвей, выражающие их характеристики. Однако из-за их нелинейного характера исключить все избыточные переменные в этом случае не удается. Три линейных уравнения системы позволяют произвести исключение трех переменных, например, напряжений u₁, u₃ и тока i₂, для которых имеем:

; ; .

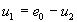
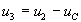
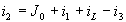
Это позволяет записать уравнения состояния цепи в нормальной форме:

правые части которых содержат избыточные переменные — ток i₃ и напряжение u₂. Они выражаются через вольтамперные характеристики резисторов, которые после исключения переменных u₁, u₃ и i₂ принимают вид:

; ; .

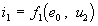
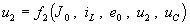
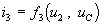
Их нелинейный характер и отсутствие явного представления для u₂ не позволяют исключить эту переменную из правых частей уравнений состояния в общем случае. Поэтому задача расчета цепи сводится к интегрированию системы:

;;.

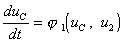
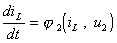
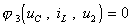
Последнее нелинейное уравнение однозначно определяет напряжение u₂ и используется через его выражения через u_C и i_L. Однако, если эту процедуру можно реализовать лишь численно, то при интегрировании уравнений состояния ее приходится выполнять на каждом шаге при каждом вычислении правых частей дифференциальных уравнений. Это увеличивает трудоемкость решения нелинейной системы по сравнению с интегрированием линейных уравнений состояния.