Уравнения узловых напряжений в прямоугольной системе координат

Уравнения узловых напряжений

Уравнения узловых напряжений (УУН) — система нелинейных (иногда линейных) алгебраических уравнений, в которых неизвестными являются напряжения в узлах электрической сети, наиболее часто применяемая для расчёта установившегося режима электрической сети.

Содержание

Описание

Установившийся режим электрических систем можно рассчитывать при различных способах задания исходных данных в зависимости от физической сути и цели расчёта. В статье рассмотрен наиболее часто встречающийся и наиболее простой случай, когда известны сопротивления и проводимости всех пассивных элементов электрической сети. Кроме того, заданы постоянные величины всех значений токов (мощности) во всех узлах, кроме балансирующего и все ЭДС, а также напряжение одного узла — базисного. При этом необходимо определить напряжения всех [math](n-1)[/math] узлов и токи во всех m ветвях.

В общем случае базисный по напряжению и балансирующий узлы могут не совпадать. Как правило, при расчётах режимов электрических систем предполагают, что эти узлы совпадают, в дальнейшем для простоты изложения предполагается, что базисным по напряжению и балансирующим является один и тот же [math]n[/math] -й узел. Число независимых уравнений по первому закону Кирхгофа равно числу независимых узлов [math](n-1)[/math] . Уравнение первого закона Кирхгофа для [math]n[/math] -го узла является следствием уравнений для остальных [math](n-1)[/math] узлов и не входит в число независимых уравнений.

Если в качестве неизвестных принять [math](n-1)[/math] узловых напря¬жений, то установившийся режим можно описать только узловыми уравнениями, вытекающими из первого закона Кирхгофа и закона Ома [1] , [2] , [3] , [4] . Уравнения узловых напряжений следуют из первого закона Кирхгофа, если все токи в ветвях выразить через узловые напряжения и проводимости ветвей. Число уравнений узловых напряжений равно числу независимых узлов [math](n-1)[/math] .

Уравнения баланса токов представляют собой простейшую форму уравнений, описывающих установившиеся режимы. Существуют две математические модели уравнений узловых напряжений:

Отличительной особенностью этих моделей является то, что линейная модель предполагает задание комплексных значений токов, в отличие от нелинейной модели, которая предполагает задание активной и реактивной мощностей. В большинстве задач нагрузки в узлах задаются активной и реактивной мощностями, по этой причине обычно используется нелинейная модель.

Вывод уравнений узловых напряжений

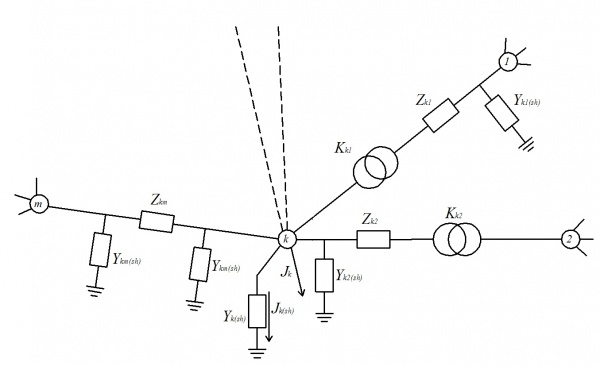
Для формирования УУН рассмотрим представленную на рис. 1 часть схемы замещения:

Первый закон Кирхгофа для к-го узла:

Наличие знака сопряжения в этом выражении обусловлено тем, что для идеального двухобмоточного трансформатора выполняется закон сохранения мощности [math]\dot=\dot=\hat\dot=\hat\dot[/math] , где индексами «Н» и «В» обозначены соответственно низшая и высшая обмотки трансформатора, поэтому, если [math]\dot=\dot\dot>[/math] , то из закона сохранения следует:

Подстановка полученных выражений в уравнение (1.1) с приведением подобных членов позволяет получить уравнение для k-го узла в виде:

В прямоугольной системе координат

В данной системе комплексные величины [math]\displaystyle \underline_, \dot>, \dot>[/math] представляются в виде

для проводимости справедливо следующее:

получаем, что [math]\displaystyle \underline=g-jb,[/math]

но для удобства расчёта матрицы проводимостей будем использовать соотношение

Запишем УУН для линейной ЭЭС:

левая часть данной системы характеризует токи, втекающие в k-й узел, правая часть — токи, вытекающие из того же узла, но с учетом влияния токов базы.

Подставляем (1), (2), (3) в (4), [math]\dot_б[/math] представим аналогично уравнению (1), тогда имеем следующее:

[math]\displaystyle \begin \sum_^ \left( g_ + j b_ \right) \left( U_‘ + j U_» \right) = J_‘ + j J_»- \left( g_ + j b_ \right) \left(U_<б>‘ + j U_<б>»\right), i = 1 \ldots N \end.[/math]

Сгруппируем и приведем подобные:

Сгруппируем относительно [math]j[/math] левую и правую части системы (5). Два комплексных числа равны, если равны их действительные и мнимые составляющие. Распишем в новой системе отдельно действительные и мнимые части. Получаем:

Представим данную систему (6) в матричной форме:

В случае, если [math]\dot_б=U_б+j0,[/math] система (6) преобразуется к виду:

Соответственно упрощается матричная форма записи системы (8):

Вернемся к нелинейной модели ЭЭС. Для этого перенесем составляющую токов базы системы (4) в левую часть, изменив при этом диапазон [math]i=1 \ldots (N-1)[/math] . Получаем:

Добавим, что [math]\dot ~~= P + j Q.[/math] (12)~~

~~Подставляем (11) в выражение (10), получаем следующее:~~

~~Подставляем (1), (3), (12) в (13), получаем:~~

[math]\displaystyle \begin \sum_^ \left( g_ + j b_ \right) \left( U_‘ + j U_» \right) = \frac< P_i - j Q_i >< U_i' - j U_i'' >, i = 1 \ldots (N-1)\end.[/math]

~~Раскрываем скобки, домножаем правую часть на сопряженное и группируем относительно [math]j[/math] :~~

Вынесем [math]j[/math] за знак суммы в левой части, а в правой части разобьем дробное выражение на две составляющие относительно [math]j[/math] , получим:

Преобразуем систему (14) к виду, аналогичному системе (8), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса токов:

Выведем систему нелинейных УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей. Для этого домножим систему (13) на [math]\hat[/math] , получаем:

~~[math]\displaystyle \begin\left(U_i’-jU_i»\right)\sum_^\left(g_+jb_\right)\left(U_‘+jU_»\right)=P_i-jQ_i\end, i=1 \ldots (N-1).[/math]~~

~~Вносим сопряженный комплекс напряжения под знак суммы и группируем относительно [math]j[/math] , имеем:~~

Преобразуем систему (17) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в прямоугольных координатах в форме баланса мощностей:

В полярной системе координат

~~Комплексное число можно представить в алгебраической, показательной и тригонометрической формах:~~

~~[math]\displaystyle \dot=U_k’+jU_k» = V_k \cdot e^ = V_k \big(\cos(δ_k)+j \sin(δ_k)\big).[/math]~~

Для того, чтобы вывести УУН в форме баланса мощностей в полярной системе координат, необходимо в систему (16) подставить показательную запись комплексного числа [math]\dot[/math] . Выполнив это, получим:

[math]\displaystyle \begin V_i e^ <-j δ_i>\sum_ \limits^ (g_ + j b_) \cdot V_k \cdot e^ = P_i — j Q_i \end, i= \overline< 1 \ldots (N-1) >.[/math]

~~Переносим экспоненты в одну сторону:~~

~~[math]\displaystyle \begin V_i\sum_\limits^V_k(g_+jb_) \cdot e^ \cdot e^<-jδ_i>=P_i-jQ_i\end, i= \overline< 1 \ldots (N-1) >.[/math]~~

~~Используя свойство степеней, выполним преобразования:~~

~~[math]\displaystyle \begin V_i\sum_\limits^ V_k (g_+jb_) \cdot e^ = P_i — jQ_i\end, i= \overline< 1 \ldots (N-1) >.[/math]~~

~~Переходим к тригонометрической форме:~~

~~[math]\displaystyle \begin V_i\sum_\limits^ V_k \bigg( \big(g_ + jb_ \big) \big( \cos(δ_k-δ_i) + j \cdot \sin(δ_k-δ_i) \big) \bigg) = P_i-jQ_i \end, i= \overline< 1 \ldots (N-1) >.[/math]~~

~~Группируем относительно [math]j[/math] :~~

Преобразуем систему (19) к виду, аналогичному системе (15), и получаем нелинейную систему УУН для сети переменного тока в полярных координатах в форме баланса мощностей:

Методы решения

~~Основные методы решения системы уравнений узловых напряжений:~~

Метод Гаусса-Зейделя — это один из самых первых разработанных методов. Обычно показывает более медленную сходимость по сравнению с другими итерационными методами. Основными особенности — это малое использование памяти и не требуется матричная алгебра.
~~Метод Якоби.~~
~~Метод Z-матриц.~~
~~Метод Ньютона-Рафсона — один из самых популярных методов решения, основанный на разложении в ряд Тейлора.~~
~~Метод голоморфного встраивания — прямой метод расчёта на основе комплексного анализа.~~

Алгоритмы — шпоры (Final). 1 Области рационального использования средств вт. Характеристики каждой из областей

Название	1 Области рационального использования средств вт. Характеристики каждой из областей
Анкор	Алгоритмы — шпоры (Final).doc
Дата	14.05.2018
Размер	2.65 Mb.
Формат файла
Имя файла	Алгоритмы — шпоры (Final).doc
Тип	Документы #19216
страница	4 из 6

Подборка по базе: Криптографические средства.doc, Основные понятия и определения в области организации вычислитель, Использование плазмид в генно-инженерных исследованиях, в разраб, курсовая работа Предупреждение преступлений, связанных с незакон, 2 Лекция Технические средства ИТ.doc, АСУТП Цеха добычи нефти и газа на базе технических средств.rtf, Жамбалова Сарана Эрдыниевна. Средства при язвенной болезни желуд, Демо-Синергия-Программные и аппаратные средства информ. безоп..d, По страницам Красной книги Брестской области.docx, Основы рационального питания.doc

З6’ Решение уравнений установившегося режима на основе L-H факторизации матрицы коэффициентов. Вычислительная схема прямой и обратной подстановки.

1-й этап:

2-й этап:

Решается обратной подстановкой

только везде вместо g -> q

37’ L-H факторизация матрицы коэффициентов системы линейных алгебраических уравнений (матрицы А). Алгоритм вычисления элементов факторизованной матрицы.

38’ Алгоритмическая и программная реализация L-H факторизации матрицы А.

Subroutine lhfact (A,n,l)

Совмещает достоинства методов обращения и Гаусса:

1)Операция факторизации только 1 раз → слабозаполнен. Матрицы L и H.

2)Вычисления существенно проще Гаусса, где на каждой итерации пересчит. матрица; алгоритмич прост.

“-“ ген. узлы только неопорные

Вывод: ↓ объем вычислений и объем требуемой памяти.
Алгоритм см билет 36!

39’/41’ Методы, используемые для расчета УР при записи узловых уравнений в форме баланса токов. / Методы, применяемые для решения комплексного узлового уравнения в форме баланса токов.
1) Метод Зейделя

— прост в алгоритмическом отношении

— естественным образом учитывает слабую заполненность матрицы узловых проводимостей

— нечувствителен к начальным приближениям
2) Метод Гаусса

— важным достоинством является высокая скорость решения

— надо хранить в памяти как исходную, так и пересчитанную матрицы

— на каждом шаге прямого хода надо выбирать главный элемент
3) Метод обращения матрицы Y

— обращение матрицы узловых проводимостей проводится 1 раз

— из слабозаполненной матрицы Y получается сильнозаполненная Z
4) LH-факторизация

Совмещает достоинства методов обращения и Гаусса.

— операция факторизации производится 1 раз => слабозаполненные матрицы L и H

— вычисления существенно проще метода Гаусса, где на каждой итерации пересчитывается матрица; алгоритмически прост

— может использоваться только с НЕОПОРНЫМИ ген. узлами.

=> малый объем вычислений и памяти ПК.

40’ Методы расчета режимов, основанные на сочетании методов Зейделя и Гаусса. Достоинства и недостатки.

Матрицу Y разбиваем на блоки, выделяя блок генераторных и опорных узлов.

Решая ур-е (1) методом Зейделя относительно напряжений в ген. оп. Узлах, получим:

Ур-е (4) решаем на основе метода Гаусса, ищем комплексы напряжений в нагрузочных узлах.

Только метод Зейделя даст возможность учесть опорные ген. узлы.

42’ Методы расчета установившегося режима, требующие разделения узлового уравнения в комплексной форме на два уравнения с действительными коэффициентами. Прямоугольная и полярная системы координат.
Поскольку брать производные по комплексным величинам

нельзя => переходим от записи в комплексном виде к 2м уравнениям с веществ. коэффициентами.

(n-1) ур-й с компл. → (2n-2) с веществ.

Пр. Метод Ньютона

В зависимости от формы записи эффективность методов м.б. различна, т.е может отличаться сходимость и время расчета(кол-во итераций).

43’ Узловое уравнение в форме баланса мощности, записанное в прямоугольной системе координат.

44’ Узловое уравнение состояния эл. сист. в форме баланса S при записи напряжений в полярной, а проводимостей – в прямоугольной системах координат.

45’ Узловое уравнение состояния эл. сист. в форме баланса мощности, записанное в полярной системе координат.

46’ Возможные формы записи нелинейных узловых уравнений установившегося режима для решения их методами, требующими разделения комплексных переменных на действит.сост.
1)узловые уравнения в форме баланса токов в прямоугольной системе координат

3)узловые уравнения в форме баланса мощности в прямоугольной системе координат

4)—//——//— в полярной системе координат

47’ Метод Ньютона. Решение узлового уравнения методом Ньютона, записанного в прямоугольной и полярной системе координат.

1)Начальные приближения

2)В точке начального приближения данная система линеаризуется путем разложения в ряд Тейлора и отбрасыванием нелинейных частей.

Т.о. метод Ньютона сводится к многократному решению (на каждой итерации) СЛАУ.

Прямоуг. сист. коорд.

Полярная ;

48’/49’ 3ависимость размерности матрицы Якоби от формы представления генераторных узлов и системы координат, в которой записаны узловые уравнения в форме баланса мощности.

Неопорный Рг, Qг

Опорный Pг,Uг

2(n-1) х 2(n-1)

[2(n–1)–k] х[2(n–1)–k]

Опорные: k- опорных узлов

— входит в уравнение баланса Q

Вывод: При опорных генераторных узлах кол-во уравнений в полярной форме снижается (при решении уравнения в форме баланса мощности)

50’ Аналитическое выражение элементов матрицы Якоби узловых уравнений в форме баланса мощности, записанных в полярной системе координат.

При решении уравнений установившегося режима, записанных в форме баланса мощности, предпочтительным является решение в полярной системе координат:

50’ Продолжение.

С билетом тебе не повезло. Улыбайся преподу 

51’ Свойства матрицы Якоби. Свойства метода Ньютона.

2) Структурно-симметричная, но числовой симметрии нет:

Структурная симметрия облегчает учет слабой заполненности, поиск и хранение ненулевых элементов.

3) Диагонально-доминирующая: Св-ва совпадают со св-вами м.Y

1) Сильная чувствительность к начальным приближениям.

2) Квадратичная сходимость

1. При отсутствии активных ограничений:

– Наличие резервов акт. и реакт. мощности, – Большой Кз по статической устойчивости, – Отсутствие перегрузок по линиям

2.При наличии активных ограничений:

– Дефицит Q, – Предел по станциям (вышли на ограничения по генерат. узлам), – Pг, Uг, Pг,Qг

3.Сходимость может ухудшиться при плохой обусловленности матрицы Якоби

(режимы, близкие к пределу по статике; резко неоднородная сеть)

4.Погрешности исходных данных влияют на сходимость метода Ньютона, решение системы уравнений по Гауссу.

5.Хорошо согласуется с методами решения оптимизац-ых задач.

6.Трудоемок в части алгоритмического представления.

52’ Модификации метода Ньютона

Метод Ньютона основан на решении всех уравнений системы на каждой итерации, это повышает вычислительную эффективность. Применение этих методов требует перехода от (n-1)-го уравнений с комплексными к (2n-2)-м ур-ям с вещественными коэффициентами и переменными. Это связано с тем, что применение этих методов требует диффер. ур-й по искомым переменным (а производные по комплексным переменным не определены). Кроме того, для общего случая задания оп. генер. узлов (P, U), искомые переменные Q, δ– вещественные. Переход осуществляется на основе записи компл. чисел в прямоуг. или полярной системах координат.

1) В мет. Н с обращением матрицы Якоби СЛАУ решается на каждой итерации относительно вектора приращения независимых перем. с использованием обратной матр. Якоби:

	значения на каждой ит. можно опред. по выражению:
	[ 1]

[ 2]
2) Введение параметра t(0

53’ Модифицированный метод Ньютона. Сущность и область

Основан на том, что если Δx ( k ) → 0, то и ΔW(x ( k –1) ) → 0, т.е. можно вычислять матрицу Якоби 1 раз.

Эту матрицу можно однократно факторизовать и использовать в процессе итераций в факторизованном виде, что значительно уменьшает объем вычислений на каждой итерации.

Особенность: из-за невысокой сходимости этот метод применяется только для нетяжелых режимов.

Метод узловых (потенциалов) напряжений

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.

Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.

Метод узловых потенциалов примеры решения задач

Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

Рис.1. Схема постоянного тока

Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.

Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ₁, φ₂, φ₃. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.

В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения

имеют следующий смысл:

– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J₁₁ – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:

Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.

В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что

Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.

Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Рис.2. Моделирование в Multisim

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.

источники:

http://topuch.ru/1-oblasti-racionalenogo-ispolezovaniya-sredstv-vt-harakteristi/index4.html

http://electrikam.com/metod-uzlovyx-potencialov-napryazhenij/