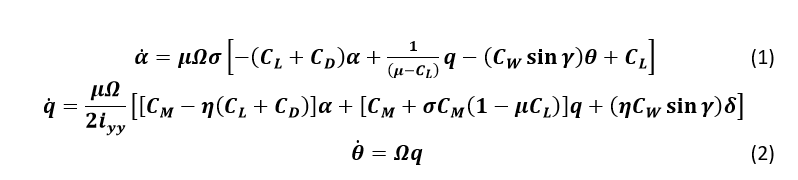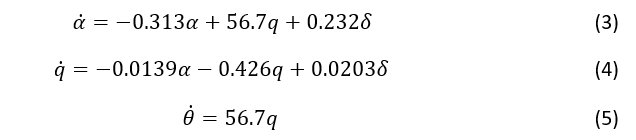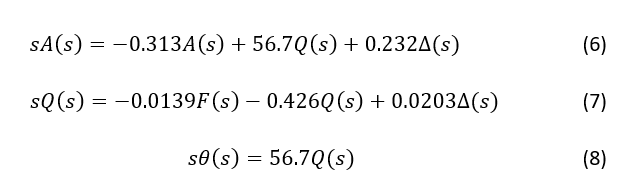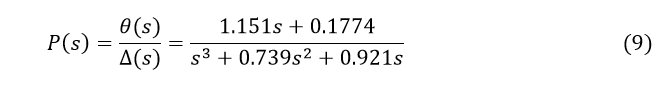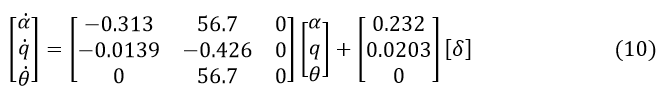Уравнения вращательного движения летательного аппарата

Оптимизация конструктивных параметров летательных аппаратов

Оптимизация конструктивных параметров летательных аппаратов

Дифференциальные уравнения движения летательных аппаратов (ЛА), будем называть математической моделью движения ЛА.

Если за признак классификации взять постоянство массы ЛА в полёте, то можно говорить о математических моделях движения ЛА постоянной и переменной массы.

К основным теоремам, используемым при составлении уравнений движения ЛА, относятся теоремы об изменении количества движения, изменении кинетического момента, изменении кинетической энергии. Распространение перечисленных классических теорем на динамику ракет, принадлежащих к классу тел переменного состава (массы), проводятся на основе так называемого принципа затвердевания, формулируемого следующим образом: уравнение движения тела переменного состава можно представлять в форме уравнений движения тела постоянного состава, имеющую мгновенно зафиксированную (затвердевшую) массу. В число сил, действующих на тело в рассматриваемый конкретный момент, включаются внешние силы, реактивные силы Кориолиса и вариационные силы [1, 2,5].

Характер движения оперенного летательного аппарата (ОЛА) вокруг центра масс существенно зависит от способа стабилизации его в полете. В настоящее время широко применяются два способа стабилизации летательных аппаратов (ЛА): вращением и оперением [2, 3].

К причинам, вызывающим колебания неуправляемых ЛА относительно центра масс, относятся следующие основные баллистические факторы.

1. Эксцентриситет силы тяги (МΔ) относительно центра массы ЛА, создается благодаря тому, что вектор силы тяги не совпадает с центром массы ЛА (рис. 2).

2. Начальные возмущения в момент пуска, к которым относят: первоначальный толчок, состоит в получении ЛА начальной угловой скорости вращения () относительно экваториальной оси; начальный угол () отклонения продольной оси ЛА от направления вектора скорости в момент пуска.

3. Аэродинамическая асимметрия ЛА (перекос, деформация и несимметричность формы элементов стабилизатора и т. п.), которая приводит к появлению дополнительных аэродинамических моментов, вызывающих колебания ЛА относительно центра масс (рис. 1).

Следует отметить, что эксцентриситет силы тяги и центра масс, а также аэродинамическая асимметрия прежде всего обусловлены производственными и эксплуатационными причинами.

Для изучения влияния перечисленных факторов на кучность использована система дифференциальных уравнений (СДУ) движения неоперенного летательного аппарата (НЛА) в возмущенной среде.

Получение математических моделей, описывающих состояние ЛА, имеет своей целью, как правило, определение искомых параметров движения: компонентов скорости движения центра масс, угловой скорости ЛА относительно его центра масс, углов, характеризующих ориентацию аппарата, и, наконец, координат центра масс, по которым может быть построена траектория движения ЛА. В качестве независимой переменной (главного аргумента) в математической модели движения ЛА выступает текущее время t. Основу математической модели, характеризующей состояние ЛА, составляют дифференциальные уравнения движения. Для того чтобы получить их решения в конечной форме, должны быть однозначно заданы начальные условия и определены силы, находящиеся в правых частях дифференциальных уравнений. При этом несущественно, в какой форме задаются воздействия (детерминированный или стохастический подход), важно, чтобы принятая модель сил характеризовалась полной информацией об их значениях в рассматриваемом интервале времени. Именно эта полная совокупность сил, определяющая вид входных воздействий, и будет характеризовать при помощи фазовых координат состояние ЛА в данный и последующий моменты времени [1, 5]

Дифференциальные уравнения пространственного движения получены проектированием на оси полускоростной и полусвязанной систем координат (рис 1, 2) [3, 4] общих векторных уравнений, выражающих содержание теорем о производных по времени от векторов количества и момента количества движения:

(1)

В качестве составляющих главного вектора действующих сил были учтены такие силы: сила лобового сопротивления; подъемная сила; сила тяги; сила Кориолиса, возникающая за счет истечения пороховых газов; силы, вызванные эксцентриситетом тяги и центра масс; силы, вызванные вращением Земли.

Составляющими главного момента количества движения учитывались следующие моменты: опрокидывающий (для ОЛА – стабилизирующий) момент; экваториальный демпфирующий момент; момент трения; момент Кориолиса, возникающий за счет истечения пороховых газов; моменты, вызванные эксцентриситетом тяги и масс; моменты, вызванные вращением Земли.

Уравнения вращательного движения неоперенного летательного аппарата около его центра масс являются динамическими уравнениями Эйлера, для которых существует наиболее простое представление в проекциях на полусвязанные оси С (рис. 2) [3, 4].

1. Уравнения движения ЛА при наличии перекоса и смещения с оси симметрии вектора силы тяги

При исследовании этого вопроса будем иметь в виду то, что ЛА все же является телом вращения, причем его ось симметрии одновременно является и осью динамической симметрии. В рассматриваемом случае к ЛА будут приложены следующие дополнительные силы и моменты:

— вследствие смещения и перекоса вектор силы тяги раскладывается на две составляющие, одна из которых параллельна оси симметрии, а вторая – ей перпендикулярна. Вследствие малости угла наклона вектора силы тяги к оси симметрии составляющую, параллельную этой оси, можно принять равной силе тяги;

— вследствие эксцентриситета силы тяги в плоскости сξη (рис.2) возникает отклоняющий реактивный момент МΔ, величина которого равна произведению силы тяги Р на эксцентриситет Δ, стремящийся вращать ЛА относительно центра масс.

Учтем также момент от косо поставленного оперения, который направлен вдоль оси симметрии ЛА и описывается соотношением:

(2)

где – угол наклона оперения, L – длинна ЛА, – площадь поперечного сечения ЛА, –массовая плотность воздуха, V – скорость ЛА, – аэродинамический коэффициент, А – полярный момент инерции.

С учетом дополнительных сил и моментов, создаваемых перекосом и смещением с оси симметрии вектора силы тяги, уравнения будут иметь вид [4]:

(3)

где .

Рассмотрим, каким же образом влияют конструктивные параметры ЛА на величину характеристик рассеивания по дальности и по направлению .

Расчет характеристик рассеивания с учетом конструктивных параметров ЛА можно провести по зависимостям [5]:

(4)

.

Поправочные коэффициенты по дальности:

на изменение – угла бросания, – начальной скорости, – баллистического коэффициента, , – углов нутации, , – угловых скоростей нутации, – линейного эксцентриситета силы тяги, – углового эксцентриситета силы тяги, – угла наклона сопел, , – линейных эксцентриситетов центра масс, – угловых эксцентриситетов центра масс, – угловой скорости собственного вращения ЛА, – времени выключения реактивного двигателя, – угла наклона оперения, – диаметра оперения, – углов нутации в точке выключения двигателя, – угловых скоростей нутации в точке выключения двигателя, – времени работы реактивного двигателя, – дальность полёта ЛА. Коэффициенты, характеризующие разброс соответствующего параметра (фактора): , , , , , , , , , , , , , , , , , , , , , , , , , , , , , . Поправочные коэффициенты по дальности рассчитаны с помощью СДУ(7).

Проведенные расчеты с помощью зависимостей (4, 8) показали, что для получения оптимальных характеристик рассеивания по дальности и по направлению , а также для обеспечения устойчивого полета ОЛА, эксцентриситет силы тяги не должен превышать ∆ мм, угловой аэродинамический эксцентриситет (рис. 4, 7).

2. Влияние асимметрии масс на полет летательных аппаратов

Рассмотрим случай, когда центр масс не лежит на геометрической оси симметрии ЛА, которая, в свою очередь, уже не является главной центральной осью инерции. Будем считать, что вектор силы тяги лежит на геометрической оси симметрии, а центр масс смещен с нее на некоторую величину ε (рис. 1). Данное смещение называется эксцентриситетом силы тяжести. Все оси координат связываем с центром инерции, а положение главных центральных осей Сξ1,η1,1 относительно связанных осей определяем с помощью малых углов γ1 и γ2 (рис. 2).

Учитывая изложенное выше и данные работы [5] получим уравнения вращательного движения с учётом асиметрии центра масс в следующем виде:

Система уравнений (5) отличается от системы (3) наличием в правой части колеблющихся слагаемых, обусловленных асимметрией масс. Заметим также, что в результате асимметрии в правой части первого уравнения системы (5) появляется почти постоянный подкручивающий момент, обусловленный силой тяги , поэтому даже невращающийся ОЛА при наличии асимметрии получает с течением времени угловую скорость собственного вращения.

При наличии разного рода асимметрии, особенно если система попадает в «резонансный» режим, существенно изменяется правая часть уравнения, описывающего изменения скорости полета. Последнее означает, что движение ОЛА будет происходить не по расчетной траектории, и в результате кучность ухудшится.

Расчеты, проведенные по зависимостям (4), (8) для ЛА: «Град», «Ураган» для различных дальностей полёта и различных тормозных колец (без тормозного кольца, с большим тормозным кольцом и малым тормозным кольцом), показали, что для получения оптимальных характеристик рассеивания линейный эксцентриситет центра масс не должен превышать ; угловой (рис 5, 8).

3. Влияние силы и момента Кориолиса за счет истечения газов из сопла

Сила и момент Кориолиса возникают в результате движения пороховых газов по камере и соплу (при наличии угловой скорости вращения ЛА, которую обозначим Ω) (рис. 3).

Элементарная сила Кориолиса определится по зависимости:

(6)

где dm = ρ∙σ; ρ – плотность газов, σ – свободная от пороха площадь сечения, U – относительная скорость истечения газов.

С учётом размеров пороховой шашки получим силу и момент Кориолиса за счёт истечения газов [4]:

где , ; массовый расход газов через сопло; эффективная скорость истечения газов; – расстояния, указанные на рис. 3.

Сравнительная оценка показала, что влияние силы Кориолиса невелико и ею можно пренебречь, а момент силы Кориолиса можно сравнить с экваториальным демпфирующим моментом и его необходимо учитывать [4].

Учитывая уравнения 3, 5, 6 и данные работы [4], система дифференциальных уравнений пространственного движения НЛА будет иметь вид:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

В данной СДУ описано движение тела (ЛА) переменной массы в которых учтены: силы лобового сопротивления, подъемная сила, сила тяги, сила Кориолиса за счёт истечения пороховых газов, силы, вызванные эксцентриситетом тяги и центра масс, силы, вызванные вращением Земли, опрокидывающий (для ОЛА – стабилизирующий) момент, экваториальный демпфирующий момент, момент трения, момент Кориолиса за счёт истечения пороховых газов, моменты, вызванные эксцентриситетом тяги и центра масс, моменты, вызванные вращением Земли. Все применяемые обозначения введены в работах [2, 3, 5]

Система дифференциальных уравнений была решена при помощи численного интегрирования методом Рунге-Кутта четвертого порядка.

Экспериментальные характеристики рассеивания , взяты по данным работ [6, 7].

4. Пути улучшения кучности оперенных летательных аппаратов

Проведенные расчеты показывают, что на угловое отклонение (рассеивание) траектории неуправляемых оперенных летательных аппаратов (ОЛА), которое характеризуется углом ψk отклонения вектора скорости в конце активного участка траектории, доминирующее влияние оказывает эксцентриситет силы тяги.

Из результатов видно, что сравнительно медленное вращение оперенных неуправляемых ОЛА вокруг продольной оси приводят к резкому уменьшению влияния эксцентриситета силы тяги и асимметрии центра масс.

Расчеты, проведенные с помощью зависимостей (4) и СДУ (8) показали, что вследствие вращения рассеивание оперенных неуправляемых ЛА по направлению уменьшается в 2–2,5 раза, по дальности – в 1–1,5 раза (рис. 6,9). Таким образом, вращение оперенных неуправляемых ЛА является эффективным средством уменьшения рассеивания и значительно улучшает кучность. Для каждого оперенного неуправляемого ЛА существует некоторая оптимальная угловая скорость вращения r0, при которой рассеивание ЛА принимает оптимальное значения. Проведенные расчеты показали, что оптимальная скорость вращения при сходе с направляющей и в полете которое будет обеспечивать минимальное техническое рассеивание, составляет: для ОЛА: М21ОФ «Град» r0=20,9 рад/с; для 9М55Ф «Смерч», r0=25,1 рад/с; для 9М27Ф «Ураган» r0=22,5 рад/с (рис. 6,9).

Угол наклона оперения для обеспечения оптимальной скорости вращения r0 и устойчивого полета ЛА должен составлять для ОЛА: М21ОФ «Град» αoper=0,049 рад, для 9М27Ф «Ураган» αoper=0,054 рад, для 9М55Ф «Смерч» αoper≤0,087 рад (рис 6.9)

Вращение оперенных направляемых ЛА можно получить одним из сделующих трех способов:

1. за счет реактивного момента, создаваемого наклоном сопел ;

2. за счет придания вращательного движения в момент старта за счет винтовых направляющих;

3. за счет косопоставленного оперения.

1. Выбранная в качестве объекта исследования совокупность типов неуправляемых ЛА позволяет всесторонне изучить особенности динамики их полета и разработать рекомендации по баллистической подготовке как существующих, так и перспективных ЛА.

2. Принятая в работе математическая модель динамики полета ЛА позволяет наиболее полно исследовать особенности баллистики ЛА и определить направления её совершенствования.

3. С целью повышения достоверности результатов исследования особенностей динамики полета ЛА по современной методике, учитывающей как волновое сопротивление, так и сопротивление трения, определены коэффициенты аэродинамических сил и моментов, действующих на ЛА в полете, а также рассчитаны их инерционно-массовые характеристики [4].

4. Вопросы влияния линейного и аэродинамического эксцентриситета силы тяги и асимметрии центра масс, рассмотренные в статье, а также начальные возмущения при сходе ЛА с направляющей и в точке выключения двигателя [4] являются определяющими при расчете оптимальных характеристик рассеивания ЛА.

5. Предложенная система дифференциальных уравнений (7) позволяет выбрать оптимальные конструктивные параметры неуправляемых ЛА, обеспечивающие максимальную дальность полета и минимальное техническое рассеивание.

6. Разработанная программа решения системы дифференциальных уравнений позволяет:

а) проводить вычисления значений параметров движения ЛА с заданным по времени шагом, а также их отклонения относительно невозмущенного движения как в пределах полной траектории, так и по участкам: активном участке траектории, пассивном участке траектории;

б) исследовать поведение ЛА под действием любой совокупности возмущений;

в) производить вычисления по возмущениям, заданным как в конечном виде, так и различными законами распределения.

7. Предложенная математическая модель (4, 7) может быть использована при разработке перспективных летательных аппаратов с различными способами стабилизации.

Часть результатов, представленных в данной работе, была получена при поддержке президента Украины в рамках гранта Государственного фонда фундаментальных исследований.

1. Джамая механіка. – К.: Видавництво «Дрохва», 2004. – 415с.

2. , Лысенко баллистика. – М.: Издательство «Машиностроение», 2005. – 607 с.

3. , и др. Баллистика ствольных систем. Справочная библиотека разработчика-исследователя. – М.: Издательство «Машиностроение», 2006. – 461 с.

4. и др. Математическая модель пространственного движения ЛА на твердом топливе в атмосфере. Вестник СумГУ №2, 2008, с 1-6.

5. О движении тела, содержащего подвижную внутреннюю массу // Доклады АН. 2005, т. 405.

6. Таблицы полета М21ОФ ТС, – 74. М.: – 1975г. – 96с.

7. Таблицы полета 9М27Ф ТС, – 84РГ. М.: – 1988г. – 272с.

8. Черноусько и оптимизация движения тела, управляемого посредством подвижной внутренней массы // Прикладная математика и механика. 2006, т. 70, вып. 6. С. 915-941.

МАКЕЕВ Василий Ильич, кандидат технических наук, доцент, доцент кафедры военной подготовки Сумского государственного университета.

, доктор технических, профессор, старший научный сотрудник Института проблем машиностроения им. Подгорного НАН Украины.

Адрес: г. Харьков, ул.

БОНДАРЬ Александр Вячеславович кандидат технических наук, доцент кафедры компьютерных наук Сумского государственного университета.

Адрес: 40000, /5, кв. 16

ТРОФИМЕНКО Павел Евгеньевич, кандидат военных наук, профессор, профессор кафедры военной подготовки Сумского государственного университета.

Рис. 1 – Положение центра масс при асимметрии.

С0 – несмещённое положение центра масс ЛА; С – смещённое положение центра масс ЛА; ε1, ε – линейное значение эксцентриситета центра масс.

1

Рис. 2 – Положение новых главных центральных осей инерции ЛА при наличии эксцентриситетов центра его масс.

Рис. 3 – Параметры истечения пороховых газов через сопло. Се – центр выходного сечения сопла;

С – центр тяжести.

Рисунок 4 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, и эксцентриситета силы тяги для ЛА «Град» М21ОФ (без тормозного кольца)

Рисунок 5 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, и эксцентриситета центра масс для ЛА «Град» М21ОФ

(с малым тормозным кольцом)

Рисунок 6 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, угловой скорости вращения ЛА и угла наклона оперения для ЛА «Град» М21ОФ

(с большим тормозным кольцом)

Рисунок 7 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, и эксцентриситета силы тяги для ЛА «Ураган» 9М27Ф (без тормозного кольца)

Рисунок 8 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, и эксцентриситета центра масс для ЛА «Ураган» 9М27Ф

(с малым тормозным кольцом)

Рисунок 9 – Зависимость характеристик рассеивания ВD, Вb, BD opt,

Bb opt от дальности полёта, угловой скорости вращения ЛА и угла наклона оперения для ЛА «Ураган» 9М27Ф

ЛЕКЦИЯ 3 ТЕМА: УРАВНЕНИЯ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ТВЕРДОГО ТЕЛА. ПРОДОЛЬНОЕ И БОКОВОЕ ДВИЖЕНИЕ

Евгений Перхуров 5 лет назад Просмотров:

1 1 Направления подготовки: Авионика Аэронавигация Системная инженерия Бортовые системы управления Дисциплина: Курс, семестр, уч. год: 3, весенний, 11/1 Кафедра: 31 СУЛА Руководитель обучения: ассистент Копысов Олег Эдуардович ЛЕКЦИЯ 3 ТЕМА: УРАВНЕНИЯ ДВИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА КАК ТВЕРДОГО ТЕЛА. ПРОДОЛЬНОЕ И БОКОВОЕ ДВИЖЕНИЕ Движение ЛА, как твѐрдого тела в связанной системе координат описывается уравнениями Эйлера (шесть нелинейных дифференциальных уравнений второго порядка). Силы и моменты, входящие в эти уравнения, сложным образом зависят от высоты, скорости и режима полѐта и меняются во времени, г. к. изменяются условия полѐта, например из-за изменения массы и момента инерции ЛА в результате расхода топлива или сброса груза. При аналитическом исследовании процессов управления ЛА его уравнения движения, как правило, упрощают, рассматривая два независимые друг от друга движения: продольное и боковое. К продольному относят поступательные движения ЛА вдоль осей ОХ и ОY и вращательное движение вокруг оси O. К боковому движению относят поступательное вдоль оси O и вращательные движения вокруг осей ОХ и ОY. Продольное движение. Обобщенная математическая модель При продольном движении ЛА вектор V линейной скорости его центра масс находится в вертикальной плоскости. Внешние силы, действующие на ЛА: Р сила тяги двигателей, вектор которой направлен вдоль оси ОХ: Х а сила лобового сопротивления, вектор которой направлен против вектора V, т.е. в отрицательную сторону оси ОХ а Y а подъѐмная сила, вектор которой перпендикулярен вектору V mg вес ЛА (m масса ЛА, g ускорение свободного падения). Вращение ЛА в плоскости

2 Х а Y а возможно под действием момента М, действующего вокруг оси O а, который называется аэродинамическим моментом тангажа. В соответствии с рис. 3.1 имеют место кинематические соотношения:, (3.1) где ϑ угол тангажа θ угол наклона траектории движения центра масс (ЦМ) ЛА ω угловая скорость тангажа. Рисунок 3.1 Внешние силы, действующие на ЛА в продольном движении Вращательное движение ЛА вокруг оси O а описывается уравнением: I, (3.) где I момент инерции ЛА относительно оси O а М момент аэродинамических сил, который можно представить в виде: mba S V, (3.3) где т коэффициент момента b а — хорда крыла ρ плотность воздуха S площадь крыльев. Коэффициент т можно представлять состоящим из суммы трех слагаемых, два из которых зависят от статических параметров (α, V, δ в ) и определяют статический момент, а третий от динамических параметров ( ), и определяет демпфирующий момент.

3 3 Спроектируем силы, действующие на ЛА, на касательную к траектории полѐта (ось X) и на нормаль к ней (ось Y). Сумма проекций сил на касательную к траектории: dv m mv P cos X a mg sin. dt (3.4) При определении проекций сил на нормаль к траектории нужно иметь в виду, что при движении ЛА по искривленной траектории с радиусом кривизны r, на него действует центробежная сила инерции mv траектории), a ds = Vdt, то / mv mv mv d r. Так как r = ds/dθ (s длина дуги mv mv. r ds / d Vdt / d dt Следовательно, сумма проекций сил на нормаль к траектории: mv Y Psin mg cos. a (3.5) Сила тяги Р зависит от параметров двигателя, от внешних условий, характеризуемых скоростью полѐта V, высотой полѐта Н и параметра управления двигателем δ р, т. е. в общем виде Р = Р(V, Н, δ р ). Аэродинамические силы Х а и Y а зависят от угла атаки α, скорости полѐта V, плотности воздуха ρ и угла отклонения руля высоты δ в. Так как угол δ в практически не влияет на величины Х а и Y а, то этим влиянием пренебрегают и представляют их обычно в виде: где X a CxaS V Ya CyaS V, (3.6) C xa, C ya коэффициенты лобового сопротивления и подъемной силы, зависящие от угла атаки и скорости полета. Система нелинейных дифференциальных уравнений (3.), (3.4), (3.5) с учѐтом (3.1), (3.3), (3.6) является математической моделью продольного движения ЛА. Известно, что для пилотируемых ЛА самолетной схемы практически для всех компоновок и большинства режимов полета, собственное движение ЛА состоит из двух колебательных движений, отличающихся частотой и степенью затухания. Эти движения называются короткопериодическими и длиннопериодическими или фуго-

4 идными. Причиной возникновения короткопериодических движений является нарушение равновесия моментов вокруг оси O a, что приводит к вращению ЛА относительно ЦМ и изменению углов α и ϑ. Скорость невозмущѐнного линейного движения при этом практически не изменяется. Причиной возникновения длиннопериодических движений является нарушение внешних сил, действующих в продольной плоскости симметрии ЛА, следствием чего является изменение скорости его полета. 4 Линеаризованные уравнения продольного движения ЛА Применяя к уравнениям (3.), (3.4), (3.5) метод малых возмущений, могут быть получены линейные уравнения продольного движения ЛА. Предположим, что на исследуемом участке полета невозмущенное движение ЛА характеризуется постоянными силами X, Y, P, и параметрами V, α, ϑ, θ, H и ω z =, а параметры управления δ В, δ р также постоянны. Если исследуется участок полета, на котором параметры движения существенно меняются, его разбивают на несколько участков, на которых параметра движения можно считать постоянными. Уравнения невозмущѐнного движения ЛА на участке с постоянными параметрами следуют из уравнений (3.), (3.4), (3.5): P cos X mg sin Y P sin mg cos. Из первых двух уравнений системы следует отношение: P cos X tg, P sin Y (3.7) из которого можно заключить, что при P cos X ЛА летит горизонтально, при P cos X набирает высоту ( ), а при P cos X уменьшает высоту ( ).

5 Если в некоторый момент времени параметры движения и управления изменились на величины V. то соответствующие параметры P возмущѐнного движения принимают вид: V V V P P P. При изучении продольного углового движения ЛА в области малых изменений параметров движения первое уравнение системы (3.7) из рассмотрения можно исключить, т.к. оно представляет сумму проекций сил на ось ОХ a (рис. 3.1), не влияющих на угловое движение ЛА. При линеаризации второго уравнения системы (3.7) полагают, что проекция силы тяжести на ось OY a не оказывает влияния на угловое движение ЛА, и этой составляющей можно пренебречь. В результате известных процедур линеаризации могут быть получены простейшие уравнения продольного движения ЛА: mv Y I (3.8), где постоянные коэффициенты соответствуют исходному невозмущѐнному движению и определяются следующим образом: Y Y ( Pcos ) ( ) ( ) ( ). 5

6 Рассмотрим аэродинамические моменты в уравнениях (3.8), определяющих короткопериодическое движение ЛА. При >, что обычно имеет место, момент называется моментом продольной статической устойчивости, который является следствием воздействия набегающего воздушного потока на хвостовое горизонтальное оперение, от размеров и формы которого главным образом и зависит. При невозмущѐнном движении ЛА угол атаки и аэродинамический момент относительно поперечной оси отсутствует. Восходящие или нисходящие потоки воздуха приводят к изменению угла атаки на величину например изменения центровки ЛА. Величина, который может измениться и из-за других причин, приводит к увеличению подъѐмной силы крыльев, следствием чего является изменение высоты полѐта ЛА, и к увеличению на Y подъѐмной силы горизонтального хвостового оперения, которая приложена в центре давления (ЦД) на плече L ГО, что и создаѐт момент Y L ГО, возвращающий ЛА к прежнему углу атаки, т.е. (рис. 3.). Таким образом, момент обеспечивает продольную устойчивость ЛА, если центр давления аэродинамических сил находится за центром масс ЛА в сторону хвостового оперения. Если ЦМ и ЦД совпадают, то 6 = (нейтральный ЛА), если ЦД находится впереди ЦМ, то 7 еѐ увеличение средствами аэродинамики приводит к увеличению воздействия на ЛА аэродинамических возмущений. 7 Рисунок 3. Определение момента продольной статической устойчивости Рисунок 3.3 Определение момента демпфирования тангажа Управляющий момент появляется при отклонении руля высоты хвостового горизонтального оперения, вследствие чего изменяется его угол атаки. Физическая картина воздействия этого момента на ЛА аналогична влиянию момента продольной статической устойчивости (статической устойчивости тангажа). На руль высоты, отклонѐнный от нейтрального положения на угол, действует аэродинамическая сила Y РВ, направленная перпендикулярно набегающему потоку воздуха и приложенная в ЦД рулевой поверхности (рис. 3.4), который, как правило, не совпадает с ее осью вращения (ОВ). Сила Y РВ относительно оси вращения создает так называемый шарнирный момент, который является основным нагрузочным моментом для привода, осуществляющего разворот руля высоты. В точке, соответствующей ОВ, можно приложить две противоположно направленных силы Y РВ, равных по модулю Y РВ.

8 8 Рисунок 3.4 Определение управляющего момента по высоте Тогда можно записать равенство, Y ‘ L Y ‘ l Y L из которого P P P P следует, что управляющий момент, приложенный к ЛА, состоит из суммы шарнирного момента, действующего относительно ОВ руля и момента силы Y РВ на плече L относительно ЦМ ЛА. Вернемся к уравнениям системы (3.8) и перепишем их в переменных приращений углов тангажа где и атаки : I mv ( ) Y F. Y (3.9), F Y возмущающие момент и сипа, действующие соответственно относительно оси O а и вдоль оси OY а. Уравнения системы (3.9) перепишем в виде: где a1 a a3 a a a a a 5 a F, 6 Y Y. a I I I 4 1, a 1 5, a6. I mv mv (3.1) (3.11) Постоянные коэффициенты в (3.11), соответствующие невозмущѐнному движению, определяются следующим образом:

9 m qsb m qsl m qsb Y c, yqs (3.1) где q V / скоростной напор b хорда крыла. 9 Боковое движение Аэродинамические силы и моменты, действующие на ЛА Боковое движение ЛА включает вращение вокруг продольной оси ОХ, нормальной оси ОY и линейное перемещение вдоль оси O. Рассмотрим основные аэродинамические силы и моменты, действующие на ЛА (рис. 3.5). Предположим, что вследствие какого-либо возмущения ЛА относительно нормальной системы координат ОХ g Y g g получил крен на угол γ, после чего возмущение исчезло. Угол γ определяет положение связанной системы координат ОХY, причѐм т. О совпадает с центром масс ЛА самолѐтной схемы. Плоскости крыльев относительно плоскости Х располагаются под углом φ. При положительном крене (на правое крыло) вдоль оси O появляется составляющая mg sin силы веса ЛА, под действием которой возникает скольжение ЛА со скоростью V VXtg ( V X продольная составляющая скорости V, β угол скольжения). Вследствие скольжения нарушается симметрия обтекания крыльев воздушным потоком. Для иллюстрации указанного обстоятельства на концах правого и левого крыльев построены треугольники воздушных скоростей ( V к составляющая скорости V набегающего воздушного потока вдоль крыльев V I — составляющая, перпендикулярная вектору скорости V ), из которых следует VI V tg. Так как скорости V 1 на правом и левом крыльях направлены в разные стороны, происходит изменение их углов атаки, что иллюстрируется построением треугольников скоростей на векторах скоростей V X и V I, из которых следует V / V. При этом на правом крыле имеет место положительное приращение I X угла атаки (+ ), а на другом отрицательное ( ).

10 1 Рисунок 3.5 Определение моментов статической устойчивости крена и пути Соответственно подъемная сила правого крыла увеличится на ΔY, а левого уменьшится на ΔY. В результате относительно оси ОХ образуется момент поперечной статической устойчивости или момент статической устойчивости крена, первопричиной которого является скольжение и который обозначается в виде, х М где ( х ) х. Очевидно, что этот момент тем больше, чем больше изменение угла, величина которого в соответствии с приведенными выше соотношениями, может быть представлена в виде: VI Vtg Vxtgtg, V V V x x x откуда следует, что чем больше угол φ, тем больше момент поперечной устойчивости. Стреловидность крыльев в плане также приводит к появлению момента поперечной устойчивости. Изменение углов атаки приводит к изменению сил лобового сопротивления на крыльях: на правом крыле эта сила увеличится на величину ΔХ, а на левом умень-

11 шится на ΔХ. С появлением угла β возникает также сила Δ на вертикальном оперении. Следствием указанных сил является возникновение флюгерного момента, или момента статической устойчивости пути, который старается развернуть ЛА в сторону набегающего воздушного потока. Этот момент обеспечивает устойчивость по углу скольжения, стремясь так развернуть ЛА, чтобы установился угол скольжения, имевший место до возмущения. Момент статической устойчивости пути обозначается в виде, где ( М y ) y y. 11 Используя литературные источники, найти графические зависимости коэффициента продольного момента от угла атаки и отклонения руля высоты, зависимость коэффициентов С ха, С уа от угла атаки. Термины для занесения в тезаурус: продольное движение, боковое движение, коэффициент лобового сопротивления, коэффициент подъемной силы, невозмущенное движение летательного аппарата, момент статической устойчивости, шарнирный момент.

Моделирование системы управления самолётом

Здравствуйте!

В предыдущей статье [1] мы рассмотрели некоторые особенности применения библиотеки Python Control Systems Library для проектирования систем управления. Однако, в последнее время широко используется проектирование систем управления с помощью переменных состояния, что значительно упрощает расчёты.

Поэтому, в данной статье на примере системы управления из публикации [2] мы рассмотрим упрощённую модель автопилота с использованием переменных состояния и функций tf, ss библиотеки Control.

Физические основы работы автопилота и системы уравнений полёта

Уравнения, управляющие движением летательного аппарата, представляют собой очень сложный набор из шести нелинейных связанных дифференциальных уравнений. Однако, при определенных предположениях, они могут быть разделены и линеаризованы в уравнения продольных и боковых перемещений. Полёт самолета определяется продольной динамикой.

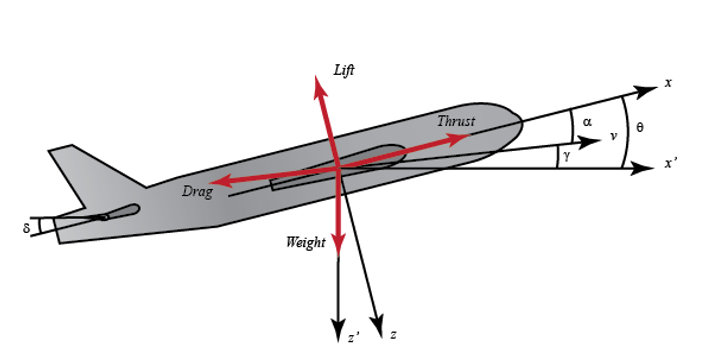
Рассмотрим работу автопилота, который контролирует высоту воздушного судна. Основные координатные оси и силы, действующие на самолет, показаны на рисунке, приведенном ниже.

Будем считать, что самолет находится в устойчивом полёте с постоянной высотой и скоростью, таким образом, тяга, вес и подъемные силы уравновешивают друг друга в направлениях координатных осей.

Мы также предположим, что изменение угла тангажа ни при каких обстоятельствах не изменит скорость полета (это нереально, но немного упростит решение). В этих предположениях продольные уравнения движения для летательного аппарата могут быть записаны следующим образом:

Обозначения переменных [3]:

Для этой системы вход будет углом отклонения 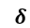, а выход будет углом тангажа

Введение численных значений в уравнения движения

Прежде чем найти передаточные функции из модели состояния пространства, подключим некоторые числовые значения, чтобы упростить приведенные выше уравнения моделирования:

Эти значения взяты из данных одного из коммерческих самолетов Boeing.

Передаточные функции

Чтобы найти передаточную функцию указанной системы, нам нужно взять преобразование Лапласа из приведенных выше уравнений моделирования. Напомним, что при нахождении передаточной функции должны приниматься нулевые начальные условия. Преобразование Лапласа приведенных уравнений показано ниже.

После нескольких шагов простых алгебраических преобразований, мы должны получить следующую передаточную функцию:

Пространство состояний объекта управления

Признавая тот факт, что приведенные выше уравнения моделирования уже находятся в форме переменных состояния, мы можем переписать их как матрицы, как показано ниже:

Для выходной характеристики модели — угла тангажа, можно записать следующее уравнение:

Исходные данные для моделирования

Следующим шагом будет выбор некоторых критериев проектирования. В этом примере мы разработаем контроллер обратной связи, так что в ответ на команду шага угла тангажа фактический угол наклона тангажа будет меньше 10%, время нарастания менее 2 секунд, время установления менее 10 секунд и установившаяся ошибка менее 2%.

Таким образом, требования к исходным данным следующие:

• Перегрузка менее 10%
• Время нарастания менее 2 секунд
• Время установления менее 10 секунд
• Стабильная ошибка менее 2%

Моделирование системы управления средствами Python

Теперь мы готовы представлять систему с использованием Python. Ниже приведен листинг модели системы управления в пространстве состояний.

Результат роботы программы:

Генерация передаточной функции по соотношению (9):

Модель пространства состояний системы управления по уравнению (10):

A = [[-3.13e-01 5.67e+01 0.00e+00]
[-1.39e-02 -4.26e-01 0.00e+00]
[ 0.00e+00 5.67e+01 0.00e+00]]
B = [[0.232 ]
[0.0203]
[0. ]]
C = [[0 0 1]]
D = [[0]]

Вывод: Средства библиотеки Python Control Systems Library позволяют проводить исследование систем управления во временной области с помощью переменных состояния.