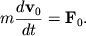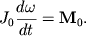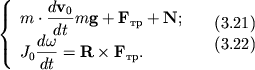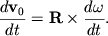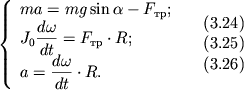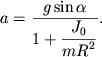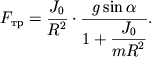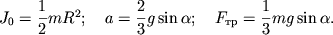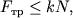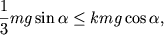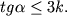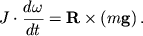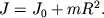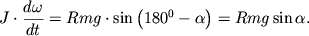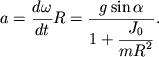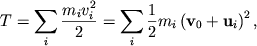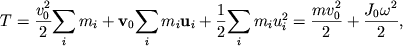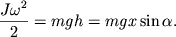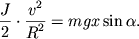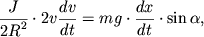Уравнения вращения тела относительно центра масс

Вращение твердого тела

Для кинематического описания процесса вращения твердого тела нужно ввести такие понятия как угловое перемещение Δ φ , угловое ускорение ε и угловая скорость ω :

ω = ∆ φ ∆ t , ( ∆ t → 0 ) , ε = ∆ φ ∆ t , ( ∆ t → 0 ) .

Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.

Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.

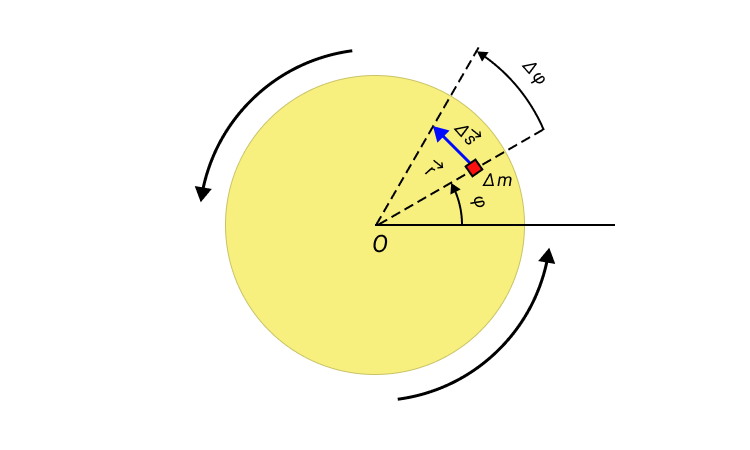
Рисунок 1. Вращение диска относительно оси, проходящей через его центр O .

Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:

в котором r – модуль радиус-вектора r → .

Между модулями угловой и линейной скоростей можно установить связь посредством равенства

Модули линейного и углового ускорения также взаимосвязаны:

Векторы v → и a → = a τ → направлены по касательной к окружности радиуса r .

Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.

Модуль ускорения выражается формулой:

a n = v 2 r = ω 2 r .

Если разделить вращающееся тело на небольшие фрагменты Δ m i , обозначить расстояние до оси вращения через r i , а модули линейных скоростей через v i , то запись формулы кинестетической энергии вращающегося тела будет иметь вид:

E k = ∑ i ν m v i 2 2 = ∑ i ∆ m ( r i ω ) 2 2 = ω 2 2 ∑ i ∆ m i r i 2 .

Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:

I = ∑ i ∆ m i r i 2 .

В пределе при Δ m → 0 эта сумма переходит в интеграл. Единица измерения момента инерции в С И – килограмм—метр в квадрате ( к г · м 2 ) . Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

В отличие от выражения, которое мы использовали для описания кинестетической энергии поступательно движущегося тела m v 2 2 , вместо массы m в формулу входит момент инерции I . Также мы принимаем во внимание вместо линейной скорости v угловую скорость ω .

Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.

В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.

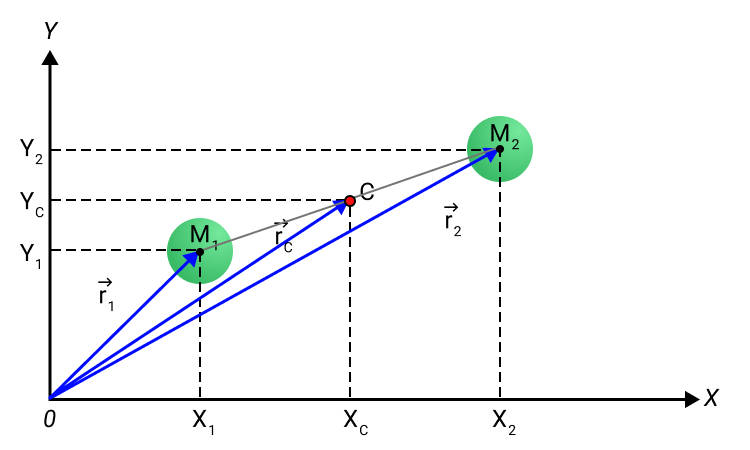
Положение x C , y C центра масс для простого случая системы из двух частиц с массами m 1 и m 2 , расположенными в плоскости X Y в точках с координатами x 1 , y 1 и x 2 , y 2 определяется выражениями:

x C = m 1 x 1 + m 2 x 2 m 1 + m 2 , y C = m 1 y 1 + m 2 y 2 m 1 + m 2 .

Рисунок 2. Центр масс C системы из двух частиц.

В векторной форме это соотношение принимает вид:

r C → = m 1 r 1 → + m 2 r 2 → m 1 + m 2 .

Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением

r C → = ∑ m i r i → ∑ m i .

Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.

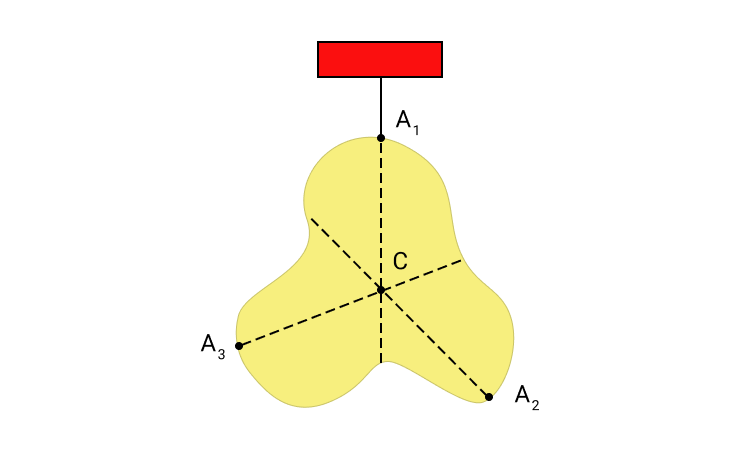
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.

Рисунок 3. Определение положения центра масс C тела сложной формы. A 1 , A 2 , A 3 точки подвеса.

На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.

Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.

Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.

Теорема о движении центра масс

Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:

E k = m v C 2 2 + I C ω 2 2 ,

где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.

Рисунок 4. Качение колеса как сумма поступательного движения со скоростью v C → и вращения с угловой скоростью ω = v C R относительно оси O , проходящей через центр масс.

В механике используется теорема о движении центра масс.

Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.

На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.

Рисунок 5. Движение твердого тела под действием силы тяжести.

Теорема Штейнера о параллельном переносе оси вращения

Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.

Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.

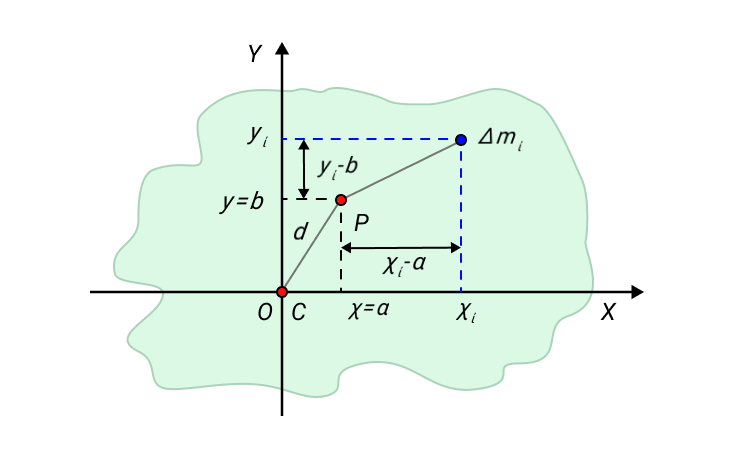
Для примера возьмем твердое тело, форма которого произвольна. Обозначим центр масс С . Выберем систему координат Х У с началом координат 0 . Совместим центр масс и начало координат.

Одна из осей проходит через центр масс С . Вторая ось пересекает произвольно выбранную точку Р , которая расположена на расстоянии d от начала координат. Выделим некоторый малый элемент массы данного твердого тела Δ m i .

По определению момента инерции:

I C = ∑ ∆ m i ( x i 2 + y i 2 ) , I P = ∑ m i ( x i — a ) 2 + y i — b 2

Выражение для I P можно переписать в виде:

I P = ∑ ∆ m i ( x i 2 + y i 2 ) + ∑ ∆ m i ( a 2 + b 2 ) — 2 a ∑ ∆ m i x i — 2 b ∑ ∆ m i y i .

Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.

Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.

Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.

I P = I C + m d 2 ,

где m – полная масса тела.

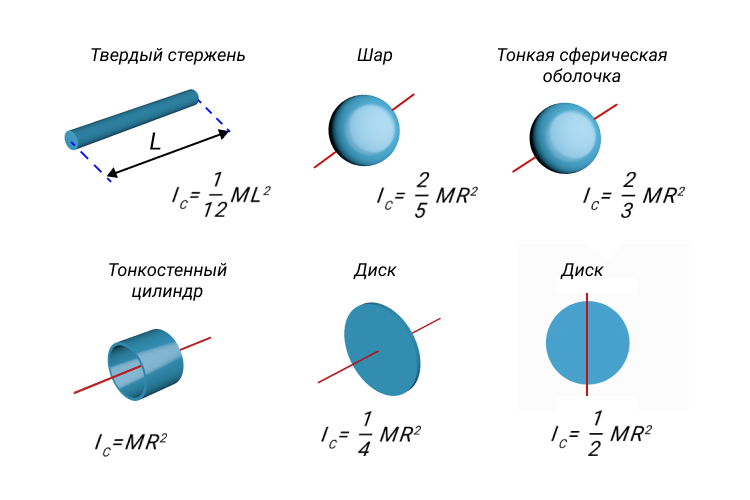
Рисунок 7. Модель момента инерции.

На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.

Основное уравнение динамики вращательного движения твердого тела

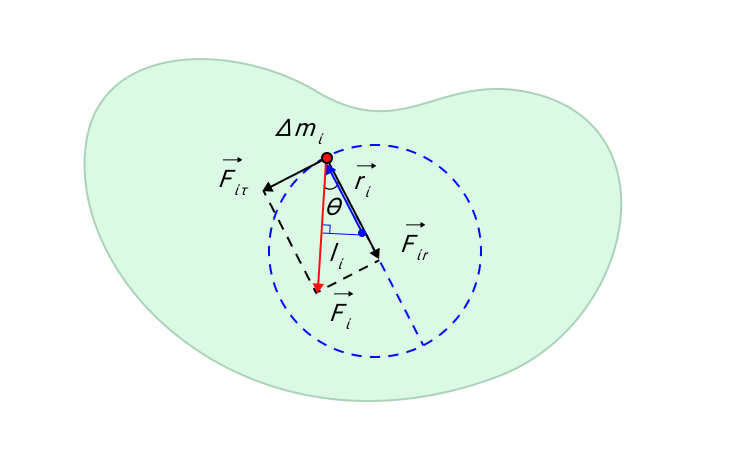
В тех случаях, когда мы имеем дело с твердым телом, которое вращается относительно неподвижной оси, мы можем обобщить второй закон Ньютона. На рисунке ниже мы изобразили твердое тело произвольной формы, вращающееся относительно некоторой оси, проходящей через точку О . Ось вращения расположена перпендикулярно плоскости рисунка.

Δ m i – это произвольный малый элемент массы, на который оказывают воздействие внешние и внутренние силы. Равнодействующая всех сил есть F i → . Ее можно разложить на две составляющие: касательную составляющую F i τ → и радиальную F i r → . Радиальная составляющая F i r → создает центростремительное ускорение a n .

Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.

Касательная составляющая F i τ → вызывает тангенциальное ускорение a i τ → массы Δ m i . Второй закон Ньютона, записанный в скалярной форме, дает

∆ m i a i τ = F i τ sin θ или ∆ m i r i ε = F i sin θ ,

где ε = a i τ r i – угловое ускорение всех точек твердого тела.

Если обе части написанного выше уравнения умножить на r i , то мы получим:

∆ m i r i 2 ε = F i r i sin θ = F i l i = M i .

Здесь l i – плечо силы, F i , → M i – момент силы.

Теперь нужно аналогичные соотношения записать для всех элементов массы Δm_i вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:

∑ ∆ m i r i 2 ε = ∑ M i .

Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.

∑ M = ∑ M i в н е ш н + ∑ M i в н у т р .

Но сумма моментов всех внутренних сил согласно третьему закону Ньютона равна нулю, поэтому в правой части остается только сумма моментов всех внешних сил, которые мы будем обозначать через M . Так мы получили основное уравнение динамики вращательного движения твердого тела.

Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.

Обычно за положительное направление вращения принимают направление против часовой стрелки.

Возможна и векторная форма записи основного уравнения динамики вращательного движения, при которой величины ω → , ε → , M → определяются как векторы, направленные по оси вращения.

Закон сохранения момента импульса

В разделе, посвященном поступательному движению тела, мы ввели понятие импульса тела p → . По аналогии с поступательным движением для вращательного движения мы вводим понятие момента импульса.

Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.

Для обозначения момента импульса используется латинская буква L .

Поскольку ε = ∆ ω ∆ t ; ∆ t → 0 , уравнение вращательного движения можно представить в виде:

M = I ε = I ∆ ω ∆ t или M ∆ t = I ∆ ω = ∆ L .

M = ∆ L ∆ t ; ( ∆ t → 0 ) .

Мы получили это уравнение для случая, когда I = c o n s t . Но оно будет справедливо и тогда, когда момент инерции тела будет изменяться в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = I ω относительно данной оси сохраняется: ∆ L = 0 , если M = 0 .

L = l ω = c o n s t .

Так мы пришли к закону сохранения момента импульса.

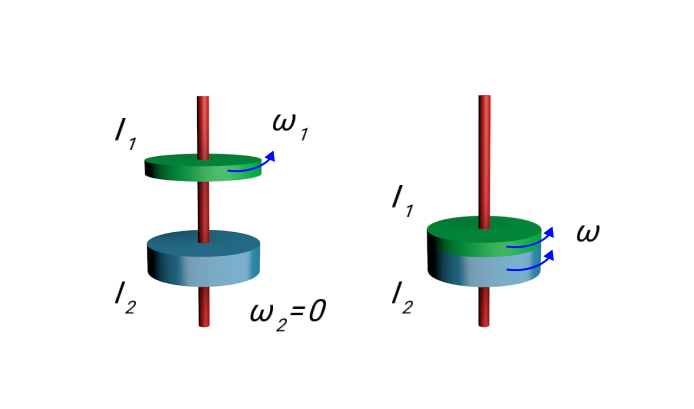
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.

Рисунок 10. Неупругое вращательное столкновение двух дисков. Закон сохранения момента импульса: I 1 ω 1 = ( I 1 + I 2 ) ω .

Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.

Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.

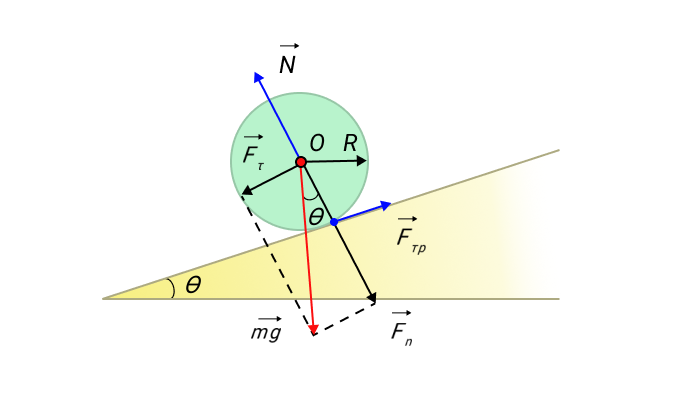
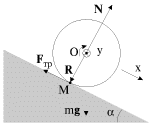
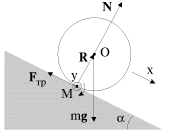
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.

Рисунок 11. Качение симметричного тела по наклонной плоскости.

Ось вращения O проходит через центр масс тела. Моменты силы тяжести m g → и силы реакции N → относительно оси O равны нулю. Момент M создает только сила трения: M = F т р R .

Уравнение вращательного движения:

I C ε = I C a R = M = F т р R ,

где ε – угловое ускорение катящегося тела, a – линейное ускорение его центра масс, I C – момент инерции относительно оси O , проходящей через центр масс.

Второй закон Ньютона для поступательного движения центра масс записывается в виде:

m a = m g sin α — F т р .

Исключая из этих уравнений F т р , получим окончательно:

α = m g sin θ I C R 2 + m .

Из этого выражения видно, что быстрее будет скатываться с наклонной плоскости тело, обладающее меньшим моментом инерции. Например, у шара I C = 2 5 m R 2 , а у сплошного однородного цилиндра I C = 1 2 m R 2 . Следовательно, шар будет скатываться быстрее цилиндра.

Уравнение движения центра масс

1. Уравнение движения центра масс

2. Уравнение моментов относительно оси, проходящей через центр масс

Особенностью плоского движения является то, что ось вращения сохраняет свою ориентацию в пространстве и остается перпендикулярной плоскости, в которой движется центр масс. Еще раз подчеркнем, что уравнение моментов (3.20) записано относительно, в общем случае, ускоренно движущегося центра масс, однако, как было отмечено в начале лекции, оно имеет такой же вид, как и уравнение моментов относительно неподвижной точки.

В качестве примера рассмотрим задачу о скатывании цилиндра с наклонное плоскости. Приведем два способа решения этой задачи с использованием уравнений динамики твердого тела.

Первый способ. Рассматривается вращение цилиндра относительно оси, проходящее через центр масс (рис. 3.11).

Система уравнений (3.19 — 3.20) имеет вид:

К этой системе необходимо добавить уравнение кинематической связи

Последнее уравнение получается из условия, что цилиндр скатывается без проскальзывания, то есть скорость точки М цилиндра равна нулю.

Уравнение движения центра масс (3.1) запишем для проекций ускорения и сил на ось x вдоль наклонной плоскости, а уравнение моментов (3.22) — для проекций углового ускорения и момента силы трения на ось y , совпадающую с осью цилиндра. Направления осей x и у выбраны согласованно, в том смысле, что положительному линейному ускорению оси цилиндра соответствует положительное же угловое ускорение вращения вокруг этой оси. В итоге получим:

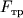
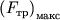
Следует подчеркнуть, что — сила трения сцепления — может принимать любое значение в интервале от О до (сила трения скольжения) в зависимости от параметров задачи. Работу эта сила не совершает, но обеспечивает ускоренное вращение цилиндра при его скатывании с наклонной плоскости. В данном случае

Если цилиндр сплошной, то

Качение без проскальзывания определяется условием

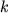
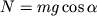
где — коэффициент трения скольжения, — сила реакции опоры. Это условие сводится к следующему:

Второй способ. Рассматривается вращение цилиндра относительно неподвижной оси, совпадающей в данный момент времени с мгновенной осью вращения (рис. 3.12).

Мгновенная ось вращения проходит через точку соприкосновения цилиндра и плоскости (точку М). При таком подходе отпадает необходимость в уравнении движении центра масс и уравнении кинематической связи. Уравнение моментов относительно мгновенной оси имеет вид:

В проекции на ось вращения (ось y)

Ускорение центра масс выражается через угловое ускорение

(3.36)

Кинетическая энергия при плоском движении.

Кинетическая энергия твердого тела представляет собой сумму кинетических энергий отдельных частиц:

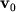
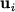
где — скорость центра масс тела, — скорость i-й частицы относительно системы координат, связанной с центром масс и совершающей поступательное движение вместе с ним. Возводя сумму скоростей в квадрат, получим:

так как 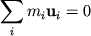(суммарный импульс частиц в системе центра масс равен нулю).

Таким образом, кинетическая энергия при плоском движении равна сумме кинетических энергий поступательного и вращательного движений (теорема Кенига). Если рассматривать плоское движение как вращение вокруг мгновенной оси, то кинетическая энергия тела есть энергия вращательного движения.

В этой связи задачу о скатывании цилиндра с наклонной плоскости можно решить, используя закон сохранения механической энергии (напомним, что сила трения при качении без проскальзывания работу не совершает).

Приращение кинетической энергии цилиндра равно убыли его потенциальное энергии:

Здесь — длина наклонной плоскости, — момент инерции цилиндра относительно мгновенной оси вращения.

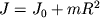
Поскольку скорость оси цилиндра 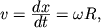то

Дифференцируя обе части этого уравнения по времени, получим

откуда для линейного ускорения 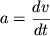оси цилиндра будем иметь то же выражение, что и при чисто динамическом способе решения (см. (3.27, 3.36)).

Замечание. Если цилиндр катится с проскальзыванием, то изменение его кинетической энергии будет определяться также и работой сил трения. Последняя, в отличие от случая, когда тело скользит по шероховатой поверхности, не вращаясь, определяется, в соответствии с (3.14), полным углом поворота цилиндра, а не расстоянием, на которое переместилась его ось.

Динамика твердого тела на данном этапе используется для тел, движущихся в сплошной среде.

В задаче о полете тела с тремя несущими поверхностями при наличии динамической асимметрии определены условия, при которых проявляются синхронизмы 1:3. С увеличением угловой скорости вращения тела около продольной оси даже на поверхности рассеивания заметно ослабление этого эффекта.

Разработана программа имитационного моделирования комплекса задач по динамике полета противоградовых ракет. С ее помощью построены таблицы введения поправок на установочные углы запуска ракет для наилучшей компенсации вредного влияния ветра.

Создана механико-математическая модель полета бумеранга. Открыта лаборатория навигации и управления.

Разработан и внедрен на аэродинамической трубе А-8 комплекс механического оборудования и сопутствующей измерительной аппаратуры для проведения динамических испытаний моделей. Определены коэффициенты демпфирования поперечных колебаний осесимметричных оперенных тел различного удлинения при раскрутке вокруг собственной оси в до- и сверхзвуковом потоках.

На основе численного решения задачи о плоских движениях аэродинамического маятника (с несущей поверхностью в виде прямоугольной пластины) в несжимаемой жидкости с учетом динамики вихрей определены области существования всех типов движения маятника, включая режимы автоколебаний и авторотации. Открыта лаборатория сверхзвуковой аэродинамики.

Также в институте компьютерных исследований проводят значимые исследования по динамике твердого тела.

Это направление исследований института связано с анализом движения твердого тела с широким применением компьютерных методов.

Компьютерные исследования в динамике твердого тела относятся к отдельной области науки — компьютерной динамике, которая устанавливает общие закономерности движения систем при помощи различных численных методов и алгоритмов.

В сочетании с аналитическими методами, достижениями топологии, анализа, теории устойчивости и других методов компьютерная динамика применяется, главным образом, в исследовании интегрируемых задач, в частности, динамических проблем теории волчков. Такой подход позволяет получить достаточно полное представление о движении, разобраться во всем его многообразии и наглядно представить себе каждое конкретное движение и его особенности.

Помимо анализа интегрируемых ситуаций в институте начато исследование случаев хаотического поведения в динамике твердого тела. Эти исследования, которые ранее почти не проводились, основаны на широком применении высокоточного компьютерного моделирования. Ожидается, что изучение этой области динамики твердого тела позволит получить в перспективе много новых интересных результатов.

Кроме того, в институте проводятся исследования с использованием методов пуассоновой динамики и геометрии, теории групп и алгебр Ли — методов, которые во многом возникли из задач динамики твердого тела.

Уравнения вращения тела относительно центра масс

При поступательном движении все точки тела получают за один и тот же промежуток времени равные по величине и направлению перемещения, поэтому скорости и ускорения всех точек в каждый момент времени оказываются одинаковыми. Поэтому достаточно определить движение одной из точек тела (например, его центра инерции) для того, чтобы полностью охарактеризовать его движение.

При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Для описания вращательного движения нужно задать положение в пространстве оси вращения и угловую скорость тела в каждый момент времени.

Любое движение твердого тела может быть представлено как суперпозиция двух вышеуказанных основных видов движения. Покажем это на примере плоского движения, при котором все точки тела перемещаются в параллельных плоскостях. Таким образом, например, происходит качение цилиндра по плоскости. Элементарное перемещение какой-либо точки тела можно разложить на два — «поступательное» и «вращательное»:

причем для всех точек тела одно и то же. Разделив на соответствующий промежуток времени dt, получим скорость точки:

где — одинаковая для всех точек тела скорость поступательного движения и — различная для разных точек тела скорость вращательного движения.

Линейная скорость точки с радиус-вектором , обусловленная вращением твердого тела, равна:

Следовательно, скорость этой точки при сложном движении тела имеет значение:

1.5.2. Движение центра инерции
(центра масс) твердого тела

Разбив тело на элементарные массы Δm_i, можно представить его как систему МТ, взаимное расположение которых остается неизменным. Любая из этих элементарных масс может находиться под воздействием внутренних и внешних сил. Напишем для каждой элементарной массы уравнение второго закона Ньютона:

где — результирующие всех внутренних и всех внешних сил, действующих на данную элементарную массу. Суммируя, для всех элементарных масс имеем:

Однако сумма всех внутренних сил, действующих в системе, равна нулю. Поэтому (1.5.5) можно упростить так:

Используя определение центра инерции, можно записать:

Дифференцируя (1.5.7) дважды по времени, можно получить:

Подставляя (1.5.8) в (1.5.6), имеем:

Следовательно, центр инерции твердого тела движется так, как двигалась бы МТ с массой, равной массе тела, под действием всех приложенных к телу сил.

1.5.3. Момент силы

Рассмотрим схему установки на Рис. 1.5.1.

Рис. 1.5.1. Схема установки для исследования
равно-ускоренного вращательного движения

Под действием груза Р крестовина будет вращаться с возрастающей угловой скоростью, и вращение будет равно-ускоренным. Варьируя величину груза Р, радиус шкива l, массу грузов m и их расстояние R от оси вращения, можно прийти к заключению, что угловое ускорение β:

1. прямо пропорционально натяжению нити f и радиусу шкива l;
2. обратно пропорционально массе грузов m и квадрату их расстояния R от оси вращения.

Следовательно, ускорение вращательного движения зависит не только от величины действующей на тело силы, но и от расстояния l от оси вращения до линии, вдоль которой действует сила. Произведение fl дает величину так называемого момента силы относительно оси вращения.

Из этого опыта следует также, что на величину углового ускорения влияет не только масса вращающегося тела, но и распределение массы относительно оси вращения. Величина, которая это учитывает, называется моментом инерции тела относительно оси вращения.

Моментом силы относительно некоторой точки О называется величина , равная векторному произведению:

где — радиус-вектор, проведенный из точки О в точку приложения силы (Рис. 1.5.2).

Рис. 1.5.2. К определению момента силы

Вектор , по определению, перпендикулярен плоскости векторов и и направлен от нас. Это — аксиальный вектор. Модуль вектора равен:

где α — угол между направлениями векторов и , а l = r sinα — длина перпендикуляра, опущенного из точки О на прямую, вдоль которой действует сила. Эта длина называется плечом силы относительно точки О.

Если можно представить силу в виде суммы сил, имеющих общую точку приложения , то формулу (1.5.10) можно записать так:

Парой сил называются две равные по величине и противоположно направленные силы, не действующие вдоль одной и той же прямой (Рис. 1.5.3). Расстояние l между прямыми, вдоль которых действуют силы, называется плечом пары сил .

Рис. 1.5.3. Момент пары сил

Покажем, что момент пары сил относительно любой точки будет один и тот же. Пусть точка лежит в плоскости, в которой действуют силы, и выполняется . Момент силы равен fl₁ и направлен к наблюдателю, момент силы равен fl₂ и направлен от наблюдателя. Результирующий момент силы направлен от наблюдателя и равен:

Полученное выражение не зависит от положения точки О на плоскости, в которой лежит пара сил.

Суммарный момент внутренних сил Силы, с которыми взаимодействуют друг с другом две любые элементарные массы, лежат на одной и той же прямой (Рис. 1.5.4).

Рис. 1.5.4. Момент внутренних сил

Их моменты относительно произвольной точки О равны по величине и противоположны по направлению. Поэтому моменты внутренних сил попарно уравновешивают друг друга, и сумма моментов всех внутренних сил для любой системы МТ, в частности, для твердого тела, всегда равна нулю.

1.5.4. Момент импульса материальной точки.
Закон сохранения момента импульса

Аналогично моменту силы введем момент импульса МТ относительно некоторой точки О:

где — радиус-вектор, проведенный из точки О в точку пространства, в которой находится МТ (Рис. 1.5.5).

Рис. 1.5.5. К определению момента импульса

Введя плечо l = rsinα, можно получить модуль вектора момента импульса в виде:

Продифференцируем (1.5.16) по времени:

Первое слагаемое равно нулю в силу того, что оно представляет собой векторное произведение векторов одинакового направления: . Вектор . Поэтому соотношение (1.5.17) можно переписать так:

где — момент приложенных к МТ сил, взятый относительно той же точки О, относительно которой рассчитан момент импульса . Для замкнутой системы из N материальных точек легко получить аналогичное (1.5.18) соотношение. В отсутствие или при взаимной компенсации внешних сил их суммарный момент , действующий на тела системы, равен нулю. В результате этого суммарный момент импульса не зависит от времени. Таким образом, формулируется закон сохранения момента импульса : момент импульса замкнутой системы материальных точек остается постоянным.

1.5.5. Уравнение динамики
вращательного движения

Если МТ вращается по окружности радиуса r (Рис.1.5.6), то момент ее импульса относительно оси вращения О равен:

Рис. 1.5.6. К выводу уравнения динамики вращательного двмжения

Пусть ω — угловая скорость вращения, тогда v = ωr, и (1.5.18) будет иметь вид:

Если вокруг оси О вращается система МТ с одной и той же угловой скоростью ω, то:

где, момент инерции системы МТ относительно оси вращения, равный сумме произведений масс МТ на квадраты их расстояний до оси вращения.

Если угловая скорость и момент инерции — переменные величины, то, подставляя (1.5.21) в (1.5.18), получим:

где М — момент внешних сил относительно оси вращения. Соотношение (1.5.22) — это основное уравнение динамики вращательного движения вокруг неподвижной оси.

Важным частным случаем является вращение неизменяемой системы МТ или твердого тела вокруг неподвижной оси. В этом случае момент инерции I остается постоянным при вращении, и уравнение (1.5.22) будет иметь вид:

Сопоставляя уравнения динамики вращательного движения с уравнениями динамики поступательного движения, легко заметить, что при вращательном движении роль силы исполняет момент силы, роль массы — момент инерции и т д. (Табл. 1.5.1).

Сопоставление закономерностей
поступательного и вращательного движений

— сила	— момент силы
— масса	— момент инерции
— линейная скорость	— угловая скорость
— линейная скорость	— угловая скорость
— линейное ускорение	— угловое ускорение
— импульс	— момент импульса

Предположим, что твердое тело может изменять свою конфигурацию в результате перераспределения масс. Пусть в результате происходит изменение момента инерции от значения I₁ до I₂. Если такое перераспределение осуществляется при отсутствии моментов внешних сил, то согласно закону сохранения момента импульса должно выполняться равенство:

где ω₁ — исходное, а ω₂ — конечное значение угловой скорости тела. Следовательно, изменение момента инерции влечет за собой соответственное изменение угловой скорости тела. Этим объясняется такое явление: человек, стоящий на вертящейся скамье, разводя руки в стороны, начинает вращаться медленнее, а, прижимая руки к туловищу, будет вращаться быстрее.

1.5.6. Момент инерции. Теорема Штайнера

Из определения момента инерции:

следует, что момент инерции — величина аддитивная. Это означает, что момент инерции тела равен сумме моментов инерции его частей. Каждое тело, независимо от того, вращается оно или покоится, обладает определенным моментом инерции.

Распределение массы в пределах тела можно охарактеризовать с помощью физической величины, называемой плотностью. Если тело однородно, то его плотность может быть вычислена так:

где m — масса, V — объем тела. Для тела с неравномерно распределенной массой соотношение (1.5.26) дает среднюю плотность. Плотность в данной точке определяется в этом случае так:

Уменьшение объема в (1.5.27) следует производить до тех пор, пока не будет получен физически бесконечно малый объем, который достаточно мал, чтобы в его пределах макроскопические свойства вещества можно было считать одинаковыми, и достаточно велик, чтобы не могла проявиться дискретность (атомарное строение) вещества.

Согласно (1.5.27), элементарная масса тела может быть вычислена так:

Следовательно, момент инерции следует записать в виде:

Если плотность постоянна, ее можно вынести за знак суммы:

Устремляя ΔV_i к нулю, можно в (1.5.30) перейти к интегрированию:

В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (Рис. 1.5.7).

Рис. 1.5.7. К расчету момента инерции диска

Разобьем диск на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r. Объем такого слоя равен:

где b — толщина диска. Поскольку диск однороден, плотность можно вынести за знак интеграла:

где R₀ — радиус диска. Применяя обозначение для массы диска , получим для момента инерции однородного диска:

В данном случае вычисление момента инерции упрощалось благодаря однородности и симметричности тела. Если бы нужно было отыскать момент инерции относительно оси О’О’ (Рис. 1.5.7), перпендикулярной к диску и проходящей через его край, вычисления оказались бы значительно сложнее. В таких случаях отыскание момента инерции облегчается, если воспользоваться теоремой Штайнера : момент инерции I относительно произвольной оси равен сумме момента инерции I C относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:

В соответствии с теоремой Штайнера момент инерции диска относительно оси О’О’ равен:

1.5.7. Работа и кинетическая энергия
вращающегося твердого тела

Если МТ вращается по окружности с радиусом r, то элементарная работа при повороте на угол dφ равна:

Такое же выражение получится и для твердого тела, так как его можно рассматривать как систему МТ, вращающихся с общей угловой скоростью ω. Роль силы в (1.5.37) играет момент внешних сил, роль линейного перемещения — угловой поворот.

Кинетическая энергия твердого тела, вращающегося с угловой скоростью ω, может быть записана так:

Это выражение напоминает соответствующую формулу для кинетической энергии МТ и может быть получено из нее формальной заменой m → I, v → ω.

© ФГОУ ВПО Красноярский государственный аграрный университет, 2013