Уравнения вращения твердого тела вокруг неподвижной точки

Вращение твердого тела вокруг неподвижной точки. Углы Эйлера

Движение твердого тела называетсявращением вокруг неподвижной точки, если во все время движения одна и та же точка твердого тела остается неподвижной. Вращение твердого тела вокруг неподвижной точки называют сферическим движением, поскольку траектория любой точки тела располагается на поверхности сферы с центром в неподвижной точке тела.

Положение тела, как правило, определяется углами Эйлера: углом прецессии , углом нутации , углом собственного вращения .

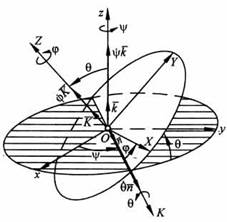
Линию OK пересечения координатных плоскостей Оху (на рис. изображена в виде заштрихованного овала) и OXY (ограничена белым овалом) назовем линией узлов. Тогда угол прецессии у определяет положение линии узлов ОК относительно неподвижной координатной оси Ох. Для изменения этого угла тело должно вращаться вокруг неподвижной оси Oz, называемой осью прецессии. Угол нутации определяет положение подвижной оси OZ относительно неподвижной Oz и равен углу между этими осями. Изменение угла сопровождается вращением тела вокруг линии узлов ОК, называемой осью нутации. Наконец, угол собственного вращения характеризует вращение тела вокруг оси OZ, называемой осью собственного вращения. В подвижной плоскости OXY это угол между линией узлов ОК и подвижной осью ОХ.

Положительное направление отсчета углов Эйлера , и противоположно направлению движения часовой стрелки, если смотреть на поворот тела с положительных направлений осей Oz, ОК и OZ соответственно.

Уравнения вращения твердого тела вокруг неподвижно точки: .

Скорости и ускорения точек тела при его вращении вокруг неподвижной точки.

Скорости и ускорения точек твердого тела при его свободном движении.

Переносное движение — поступательное движение вместе с полюсом. (Ve)

Относительное движение — вращательное движение относительно полюса. (Vr)

vM = dρ/dt = dr0/dt + dr/dt = v0 + ωr = (vM)e + (vM)r

a = dv/dt = dv0/dt + (dω/dt)*r + ω(dr/dt) = a0 + ε*r+ ω*r = a0 + a(вр) + а(ос) = (аМ)е + (аМ)r

(все что идет ниже, может не относиться к этому вопросу)

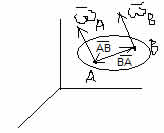
1) Полюс — т. А: vB = vA + ωS*AB

2) Полюс — т. В: vA = vB + ωB*BA = vB — ωB*AB

1) + 2) : (vB + vA) = (vA + vB) + ω*AB- ωB*AB

Сложное движение точки. Основные понятия.

Движение точки, исследуемое одновременно в основной и подвижной (подвижных) системах отсчета, называется сложным. В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения.

Рассмотрим сложное движение точки M, перемещающейся по отношению к подвижной системе O’XYZ, связанной с некоторым телом Qy которое в свою очередь совершает свободное движение по отношению к основной, условно неподвижной системе Oxyz.

Движение точки М по отношению к неподвижной системе отсчета Oxyz называется абсолютным, или сложным, состоящим из относительного движения по отношению к подвижной системе O’XYZ и переносного — движения подвижной системы отсчета O’XYZ по отношению к неподвижной системе Oxyz.

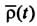
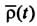
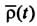
Положение точки М в подвижной системе координат O’XYZ характеризует радиус-вектор с началом в точке О’. Траектория точки М в подвижной системе отсчета называетсяотносительной траекторией и представляет собой годограф радиус-вектора . Скорость движения точки М по отношению к осям подвижной системы координат называетсяотносительной скоростью и обозначается Vr. Вектор Vr определяет скорость изменения с течением времени радиус-вектора в подвижной системе O’XYZ и поэтому выражается его относительной, или локальной, производной по времени, .
Ускорение точки М в этом движении называется относительным ускорением и обозначается аr. Вектор аr характеризует скорость изменения вектора относительной скорости Vr в подвижной системе O’XYZ и поэтому выражается относительной, или локальной, производной по времени от Vr: .

Движение подвижной системы O’XYZ по отношению к неподвижной Oxyz является для точки М переносным движением, а скорость и ускорение той неизменно связанной с подвижной
системой отсчета точки А, с которой в данный момент времени совпадает точка М, называют переносными скоростью и ускорением точки М и обозначают Ve и ае.

Переносные скорость и ускорение точки М определяются по формулам: , где вектора Vo’ и ao’ — скорость и ускорение точки О’ подвижной системы координат.

Вращения твердого тела вокруг неподвижной точки

Содержание:

Вращением твердого тела вокруг неподвижной оси называется такое движение твердого тела, при котором хотя бы две его точки остаются неподвижными. Прямая, проходящая через эти неподвижные точки называется осью вращения. Траекториями движения точек твердого тела являются окружности с радиусами равными расстояниям от заданных точек тела до оси вращения.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Вращения твердого тела вокруг неподвижной точки (сферическое движение)

Движение тела вокруг неподвижной точки (центра) называется сферическим движением. Сформулируем определение сферического движения.

Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной, а все остальные точки движутся по кругам, которые расположены на поверхностях сфер, описанных с неподвижной точки.

Одной из главных задач при изучении сферического движения является нахождение величин, характеризующих это движение: положение тела, угловые скорость и ускорение тела, вычисления скоростей и ускорений точек тела.

Рассмотрим движение тела вокруг неподвижного центра О (рис. 2.39). Выберем неподвижную систему отсчета Ox₁y₁z₁, относительно которой будем изучать движение тела, и подвижную — Oxyz, которую жестко свяжем с телом, что движется. Начало обеих систем координат расположим в неподвижном центре.

Для определения положения вращающегося тела относительно неподвижной системы координат Ox₁y₁z₁ необходимо задать относительно этой системы координат положения другой, подвижной системы координат Oxyz, скрепленной с движущимся телом. Для этого Эйлер предложил следующую теорему:

«Произвольное перемещение твердого тела вокруг неподвижной точки можно выполнить тремя последовательными поворотами тела вокруг трех осей, проходящих через неподвижную точку».

Согласно этой теореме положения тела, вращающегося вокруг неподвижной точки, определяется тремя углами. Линия ОК, вдоль которой пересекаются плоскости Oxy и Ox₁y₁ называется линией узлов. Тогда положения подвижных осей координат x, y, z (рис. 2.39) по отношению к неподвижной системе отсчета Ox₁y₁z₁ можно определить тремя углами:

,

,

.

Эти углы носят название углов Эйлера и имеют следующие наименования:

1. — угол прецессии, изменение которого означает вращение тела вокруг оси Oz₁, которая называется осью прецессии;

2. — угол нутации, изменение которого характеризует вращение тела вокруг линии узлов ОК, которая является осью нутации;

3. φ — угол собственного вращения, изменение которого означает вращение тела вокруг оси Oz, которая является осью собственного вращения.

Первый угол y, угол прецессии, который определяет положение линии узлов ОК относительно неподвижной координатной оси Ox₁, считается положительным, если он отсчитывается при повороте линии узлов ОК против часовой стрелки, если смотреть навстречу оси Oz₁.

Вторым углом Эйлера является угол нутации , угол между координатными плоскостями x₁Oy₁ и xOy, который можно измерять между перпендикулярами к указанным плоскостям — Oz₁ и Oz. Положительное направление угла — поворот против часовой стрелки оси Oz вокруг точки О, если смотреть навстречу линии узлов ОК. Угол отсчитывается от оси Oz₁.

Для полного определения положения данного тела относительно неподвижной системы Ox₁y₁z₁ необходимо задать угол между подвижной осью Ох и положительным направлением линии узлов ОК — угол собственного вращения φ. Этот угол считается положительным, если он меняется против часовой стрелки, смотря навстречу оси Oz.

При изменении угла φ тело вращается вокруг оси собственного вращения Oz, перпендикулярной плоскости, где расположены прямые ОК и O_x, образующих этот угол. Таким образом, угол φ определяет положение подвижной координатной оси Ox относительно линии узлов ОК.

Углы Эйлера широко применяются в теории гироскопа. Движение гироскопа, симметричного тела с неподвижной точкой на оси симметрии, которое очень быстро (30-40 тысяч об/мин.) вращается вокруг этой оси, можно представить составленным из трех движений, которые определяются углами , , φ . Изменение углов и имеет скорость на 1-2 порядка ниже, чем угла собственного вращения φ.

При вращении тела вокруг неподвижной точки в общем случае изменяются все три угла Эйлера: , , φ. Эти углы являются независимыми параметрами, которые определяют положение тела при сферическом движении относительно неподвижной системы координат. Задание трех углов Эйлера, как функции времени, являются необходимыми и достаточными условиями для полного описания сферического движения.

Следовательно, для определения положения тела с одной неподвижной точкой в ​​любой момент времени необходимо задать углы Эйлера как однозначные и непрерывные функции времени:

,

,

.

Уравнение является кинематическими уравнениями вращения твердого тела вокруг неподвижной точки. Если эти уравнения заданы, то в любой момент времени может быть определено положение твердого тела относительно неподвижной системы координат.

Действительно, отложим сначала в плоскости x₁Oy₁ от оси Ox₁ угол прецессии y против часовой стрелки, если он положительный, и определим положение линии узлов ОК. Далее отложим угол q от оси Oz₁, плоскость которого перпендикулярна линии узлов ОК, и определим положение оси z собственного вращения. И наконец, отложим в плоскости xOy угол φ от линии узлов против часовой стрелки, если он положительный, и определим положение оси Ox. Положение тела определено однозначно.

Теорема Эйлера – Даламбера

Произвольное элементарное перемещение тела, имеющего одну неподвижную точку, может осуществляться по одному элементарному повороту вокруг некоторой специально выбранной мгновенной оси вращения, проходящей через эту неподвижную точку.

Предположим, что положение тела, которое вращается вокруг точки О, определяется углами , , φ (как это показано на рис. 2.39).

Тогда его перемещения за элементарный промежуток времени можно представить как совокупность поворотов на углы d, d, dφ, вокруг оси Oz₁, линии узлов ОК и оси Oz соответственно. Прибавляясь, эти три поворота создадут одно действительное элементарное перемещение тела.

Сначала рассмотрим, каким будет результат сложения поворотов вокруг осей Oz и Oz₁, (рис. 2.40). При повороте на угол dφ любая точка тела, лежащего в плоскости Ozz₁ (внутри угла zOz₁), получит элементарное перемещение, которое перпендикулярно этой плоскости и численно равна , — расстояние от точки до оси Oz. Одновременно, при повороте вокруг оси Oz₁ та же точка получит обратное перемещение, которое численно равна .

Внутри угла обязательно найдется такая точка В, для которой = . Это означает, что перемещение этой точки равно нулю, и точка B будет неподвижной. Таким образом, имеем две неподвижные точки O и В, следовательно, неподвижную ось ОВ, вокруг которой происходит то самое элементарное вращение, которое составляет сумму вращений вокруг осей Oz и Oz₁.

Если теперь рассматривать вращения вокруг оси ОВ и линии узлов ОК, после аналогичных соображений придем к выводу, что элементарные повороты вокруг осей ОВ и ОК эквивалентны элементарному повороту вокруг некоторой оси ОР, проходящей через точку О.

Таким образом, ось ОР, элементарным поворотом вокруг которой тело перемещается из данного положения в соседнее, бесконечно близкое данному называется мгновенной осью вращения.

Следует заметить, что от неподвижной мгновенная ось вращения отличается тем, что ее положение меняется как в отношении системы отсчета Ox₁y₁z₁, так и в отношении подвижной системы координат Oxyz. Каждое последующее вращение происходит вокруг своей мгновенной оси вращения, которая, безусловно, всегда пересекает неподвижную точку О.

То есть, движение твердого тела вокруг неподвижной точки состоит из серии последовательных элементарных поворотов вокруг мгновенных осей вращения, которые пересекают неподвижную точку.

Геометрическое место мгновенных осей вращения относительно неподвижной системы отсчета называется недвижимым аксоидом. Неподвижный аксоид является конической поверхностью с вершиной в неподвижной точке тела, потому что все мгновенные оси пересекают неподвижную точку.

Геометрическое место мгновенных осей во вращающемся теле называют подвижным аксоидом, который также является конической поверхностью. Для каждого движения твердого тела вокруг неподвижной точки имеем пару аксоидов. Таким образом, во вреся сферического движения подвижной аксоид катится по неподвижному без скольжения, поскольку общая образующая этих аксоидов в каждый момент времени служит мгновенной осью, вокруг которой вращается тело, поэтому все точки оси неподвижные. Если подвижный аксоид катится без скольжения по неподвижному аксоиду, то происходит движение тела вокруг неподвижной точки.

Кинематические характеристики движения тела вокруг неподвижной точки

Угловая скорость:

Сделаем сначала определения угловой скорости тела, вращающегося вокруг неподвижной точки.

Угловая скорость, с которой происходит элементарный поворот тела вокруг мгновенной оси вращения, называется угловой скоростью тела в данный момент времени или мгновенной угловой скоростью тела.

Согласно этому определению, если тело вернется вокруг мгновенной оси на некоторое бесконечно малый угол dφ, то мгновенной угловой скоростью будет:

.

Угловую скорость можно изобразить в виде вектора , направленного вдоль мгновенной оси ОР (рис. 2.41).

Если учесть, что положение мгновенной оси ОР непрерывно меняется, то вектор угловой скорости будет меняться в течении времени как по модулю, так и по направлению, а конец вектора будет описывать некоторую произвольную кривую AB, которая является годографом вектора . На рис. 2.41 показаны различные положения мгновенной оси вращения OP, OP₁, OP₂ и соответственно расположенные на них векторы угловой скорости , и .

Угловое ускорение:

Второй кинематической характеристикой тела, вращающегося вокруг неподвижной точки является угловое ускорение.

Угловое ускорение тела в данный момент времени, или мгновенное угловое ускорение , которое характеризует изменение в течении времени угловой скорости по модулю и по направлению, является векторной величиной и численно равна:

.

Для нахождения расположения вектора углового ускорения можно использовать такую ​​аналогию. Как известно, вектор скорости произвольной точки равен производной от радиус-вектора этой точки по времени t и направлен вдоль касательной к траектории движения точки. В этом случае траектория точки является годографом концов радиус-векторов .

По аналогии с этим, вектор углового ускорения направлен по касательной к кривой AB в соответствующей точке. То есть, угловое ускорение можно считать, как скорость движения конца вектора .

Таким образом, вектор мгновенного углового ускорения имеет направление производной по времени от вектора мгновенной угловой скорости , он параллельный касательной к годографу векторной функции (t). Изображать угловое ускорение необходимо вектором, параллельный касательно к годографу векторов угловой скорости в данной точке, но приложенный к неподвижной точке O (рис. 2.40).

Скорости и ускорения точек тела в сферическом движении

Векторная формула Эйлера (2.54), полученная для вращательного движения тела вокруг неподвижной оси, справедлива и для сферического движения тела.

В сферическом движении в каждый момент времени тело вращается вокруг мгновенной оси OP, которая пересекает неподвижную точку O, с угловой скоростью , вектор которой расположен на мгновенной оси. Точки тела, которые принадлежат мгновенной оси OP, имеют скорости , равны нулю, как и в случае неподвижной оси вращения.

Следовательно, скорость произвольной точки М тела (рис. 2.42) определяется как векторное произведение и . А именно:

,

где — радиус-вектор точки M относительно неподвижной точки О.

Модуль скорости при этом будет равен:

,

где h — кратчайшее расстояние точки к мгновенной оси OP.

Таким образом, скорости точек тела в сферическом движении пропорциональны расстояниям от этих точек к мгновенной оси. Направление вектора скорости перпендикулярно плоскости, в которой расположены векторы и , то есть расстоянию h и направлен в сторону вращения.

Как известно, скорость точки является первой производной от радиус-вектора этой точки по времени (2.4):

.

В то же время, по векторной формуле (2.54) скорость равна , откуда:

Длина радиус-вектора , как расстояние между двумя точками твердого тела, является постоянной величиной при движении этого тела. Следовательно, уравнение (2.77) можно рассматривать как формулу для вычисления производной по времени от вектора, модуль которого устойчивый, а изменение его происходит только вследствие вращения с угловой скоростью вместе с телом вокруг неподвижной точки.

Если жестко скрепить подвижную систему координат Oxyz с телом, вращающимся вокруг неподвижной точки с угловой скоростью , так для единичных векторов , , , направленных по этим осям, модули которых постоянные, на основании (2.77) имеем:

,

,

.

Выражения называют формулами Пуассона.

Для определения ускорения точки тела, которое осуществляет сферическое движение, возьмем производную по скалярному аргументу t (время) от векторной функции скорости :

.

,

.

тогда окончательно имеем:

В отличии от вышеупомянутой формулы, здесь и — угловые скорость и ускорение вокруг мгновенных осей, первое слагаемое — вращательное ускорение:

,

второе слагаемое — осевое ускорение:

.

Движение свободного твердого тела

Рассмотрим наиболее общий случай движения твердого тела — свободное движение тела, когда оно может как угодно перемешиваться относительно неподвижной системы отсчета Oxyz (рис. 2.43).

Как известно из аналитической геометрии, положения твердого тела в пространстве можно определить тремя точками, которые не расположены на одной прямой и неизменно связаны с телом.

На девять координат этих точек наложено три ограничения, которые выражают неизменность расстояний между точками, потому что они принадлежат твердому телу. Итак, независимых параметров или степеней свободы тела будет шесть.

Смотря с другой стороны, при определении положения твердого тела можно задать три координаты одной его точки, например, точки A, которую назовем полюсом с координатами , , , и выбрать еще три параметра, характеризующих вращения тела вокруг полюса. Остальные параметры могут быть углами Эйлера , , φ (на рис. 2.43 не показаны). Совокупность шести скалярных функций времени, которые однозначно определяют положение свободного твердого тела в любой момент времени, является законом его движения:

,

,

,

,

,

.

Три первые уравнения определяют движение полюса и вместе с ним поступательное движение твердого тела. Последние три уравнения определяют движение тела относительно системы координат (то есть относительно точки A, как неподвижной).

Таким образом, с геометрической точки зрения элементарное перемещение свободного тела состоит из поступательного перемещения вместе с полюсом, при котором полюс переходит в соседнее положение , и с некоторого перемещения по отношению к осям .

Последнее перемещения по теореме Эйлера-Даламбера является поворотом вокруг мгновенной оси вращения , которая проходит через точку A.

Поскольку движением тела является совокупность элементарных перемещений, то можно его обозначить следующим образом:

«Свободное движение тела в общем случае состоит из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюс A со скоростью полюса , и ряда элементарных поворотов с угловой скоростью ω вокруг мгновенных осей вращения, которые проходят через полюс» (рис. 2.44).

Свободно движутся брошенный камень, снаряд, неуправляемая ракета тому подобное.

Основными кинематическими характеристиками движения является скорость и ускорение полюса, которые определяют скорость и ускорение поступательной части движения, а также угловая скорость ω и угловое ускорение ε вращения вокруг полюса. Значения величин этих характеристик можно определить по уравнениям.

В отдельном случае движение свободного тела может быть плоскопараллельным. Тогда вектор угловой скорости будет всегда перпендикулярен плоскости движения. При этом, как в общем случае, так и в отдельном, вращающаяся часть движения, как и значение угловой скорости ω, от выбора полюса не зависит.

Определим скорости и ускорения точек свободного тела.

Как и в случае плоскопараллельного движения, можно предположить, что скорость и ускорение точки свободного тела состоит геометрически со скорости ускорения векторов полюса и относительной скорости (ускорение) точки вокруг полюса (последние получает точка M при движении вместе с телом вокруг полюса A)

,

,

где ; ; — радиус-вектор точки M относительно полюса A; — скорость точки M относительно полюса A; — ускорение точки M относительно полюса A; ε — угловое ускорение тела.

Услуги по теоретической механике:

Учебные лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Углы Эйлера. Уравнения вращения твердого тела вокруг неподвижной точки

Углы Эйлера. Уравнения вращения твердого тела вокруг неподвижной точки

• Три степени свободы, которыми обладает объект при вращении вокруг фиксированной точки, требуют трех независимых величин для указания положения объекта относительно произвольной системы координат. Эти три значения или параметры могут быть установлены различными способами. В теоретической механике наиболее часто используются так называемые углы Эйлера, описанные ниже. Нарисуйте фиксированную систему координат через твердую неподвижную точку O Стая учитывает движения тела (рис. 73).

Зафиксируйте другую систему координат Oxyz с помощью объекта, вращающегося вокруг неподвижной точки O. Как определить положение движущегося объекта относительно системы координат X (y1z1, позиция относительно этой системы координат должна быть установлена Другая — это движущаяся система координат Oxyz, связанная с движущимся объектом. Для этой цели Эйлер предложил три независимых параметра — углы Эйлера. Первый угол прецессии φ этих углов определяет положение узла ОК линии. Это пересечение координатных плоскостей Oxtyt и Oxu относительно фиксированной координатной оси Oxt. для Рис. 73.

Линеаризация дифференциальных уравнений позволяет получить замкнутые решения таких систем, и обычно невозможно найти Интеграл строгой нелинейной системы уравнений конечного вида. Людмила Фирмаль

Когда этот угол изменяется, тело вращается вокруг оси координат Ozt, называемой осью прецессии. Положение линии узла при перемещении объекта изменяется как по отношению к системе неподвижных координат Ox ^ r ^, так и по отношению к движущемуся объекту, движущейся системе координат Oxyz. Угол Людмила Фирмаль

Особое значение в данной области техники имеет так называемая регулярная прецессия, когда угловая скорость вращения вокруг соответствующей оси вращения и фиксированной оси прецессии постоянна, а угол между этими осями (угол зажима) также остается постоянным. Это дифференциальное упражнение. Когда тело вращается вокруг фиксированной точки, во всех случаях все три угла Эйлера меняются: φ, 0 и

Поэтому, чтобы определить положение объекта с одной фиксированной точкой в ​​любой момент времени, углы Эйлера должны быть определены как однозначная функция времени. Ф = Л (0; 0 = фф = Л (4 0) Уравнение (1) является уравнением вращения твердого тела вокруг неподвижной точки. Если эти уравнения приведены. Затем вы можете увидеть положение твердого тела относительно системы координат Ox1y1r1 в любой момент времени. Обратите внимание, что углы Эйлера — не единственная комбинация трех независимых углов для объекта с одной фиксированной точкой. Существуют и другие комбинации углов, которые определяют положение одной системы координат относительно другой.

Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института