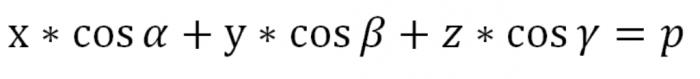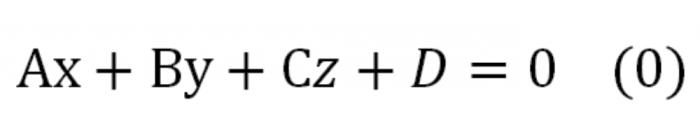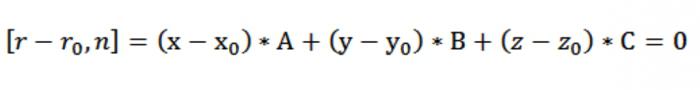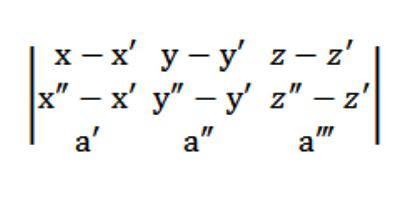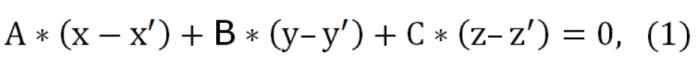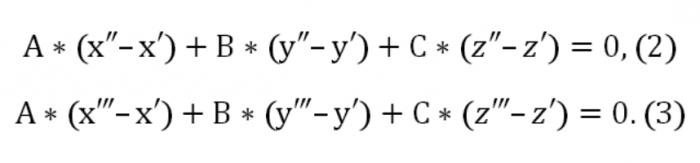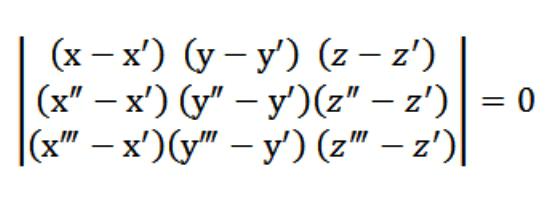Уравнения всех плоскостей параллельных плоскости

Параллельные плоскости, признак и условия параллельности плоскостей.

Эта статья посвящена параллельным плоскостям и параллельности плоскостей. Сначала дано определение параллельных плоскостей, введены обозначения, приведены примеры и графические иллюстрации. Далее приведен признак параллельности плоскостей и теоремы, позволяющие доказывать параллельность плоскостей. В заключении рассмотрены необходимые и достаточные условия параллельности плоскостей, которые заданы в прямоугольной системе координат в трехмерном пространстве, а также подробно разобраны решения примеров.

Навигация по странице.

Параллельные плоскости – основные сведения.

Дадим определение параллельных плоскостей.

Две плоскости называются параллельными, если они не имеют общих точек.

Для обозначения параллельности используется символ «». Таким образом, если плоскости и параллельны, то можно кратко записать .

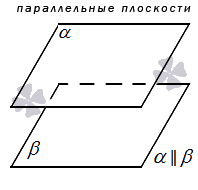
Обычно две параллельные плоскости на чертеже изображаются в виде одинаковых параллелограммов, смещенных относительно друг друга.

Отметим, что если плоскости и параллельны, то также можно сказать, что плоскость параллельна плоскости , или плоскость параллельна плоскости .

Представление о параллельных плоскостях позволяют получить, к примеру, плоскость потолка и пола. Противоположные грани куба лежат в параллельных плоскостях.

Параллельность плоскостей — признак и условия параллельности.

При решении геометрических задач часто встает вопрос: «параллельны ли две заданные плоскости»? Для ответа на него существует признак параллельности плоскостей, который представляет собой достаточное условие параллельности плоскостей. Сформулируем его в виде теоремы.

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым, лежащим в другой плоскости, то такие плоскости параллельны.

С доказательством этого признака параллельности плоскостей Вы можете ознакомиться на страницах учебника геометрии за 10 — 11 классы, который указан в конце статьи в списке рекомендованной литературы.

На практике для доказательства параллельности плоскостей также часто используются две следующие теоремы.

Если одна из двух параллельных плоскостей параллельна третьей плоскости, то другая плоскость либо тоже параллельна этой плоскости, либо совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основании приведенных теорем и признака параллельности плоскостей доказывается параллельность любых двух плоскостей.

Теперь подробно остановимся на необходимом и достаточном условии параллельности двух плоскостей и , которые заданы в прямоугольной системе координат в трехмерном пространстве.

Пусть в прямоугольной системе координат Oxyz плоскости соответствует общее уравнение плоскости вида , а плоскости — вида . (Если плоскости заданы уравнениями плоскостей в отрезках, то от них легко перейти к общим уравнениям плоскостей.)

Для параллельности плоскостей и необходимо и достаточно, чтобы система линейных уравнений вида не имела решений (была несовместна).

Если плоскости и параллельны, то по определению они не имеют общих точек. Следовательно, не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяли бы одновременно обоим уравнениям плоскостей. Поэтому, система уравнений не имеет решений.

Если система линейных уравнений не имеет решений, то не существует ни одной точки в прямоугольной системе координат Oxyz в трехмерном пространстве, координаты которой удовлетворяют одновременно обоим уравнениям системы. Следовательно, плоскости и не имеют ни одной общей точки, то есть, они параллельны.

Рассмотрим применение необходимого и достаточного условия параллельности плоскостей.

Параллельны ли плоскости и ?

Составим систему уравнений из заданных уравнений плоскостей. Она имеет вид . Выясним, имеет ли эта система линейных уравнений решения (при необходимости смотрите статью решение систем линейных алгебраических уравнений).

Ранг матрицы равен одному, так как все миноры второго порядка равны нулю. Ранг матрицы равен двум, так как минор отличен от нуля. Итак, ранг основной матрицы системы уравнений меньше ранга расширенной матрицы системы. При этом из теоремы Кронекера-Капелли следует, что система уравнений не имеет решений. Этим доказано, что плоскости и параллельны.

Заметим, что использование метода Гаусса для решения системы линейных уравнений привело бы нас к этому же результату.

Необходимое и достаточное условие параллельности плоскостей можно сформулировать иначе.

Для параллельности двух несовпадающих плоскостей и необходимо и достаточно, чтобы нормальный вектор плоскости и нормальный вектор плоскости были коллинеарны.

Доказательство этого условия основано на определении нормального вектора плоскости.

Пусть и — нормальные векторы плоскостей и соответственно. Условие коллинеарности векторов и записывается как , где t – некоторое действительное число.

Таким образом, для параллельности несовпадающих плоскостей и , нормальными векторами которых являются векторы и соответственно, необходимо и достаточно, чтобы существовало действительное число t , для которого справедливо равенство .

Известно, что в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость проходит через три точки , а плоскость определяется уравнением . Докажите параллельность плоскостей и .

Сначала убедимся, что плоскости и не совпадают. Это действительно так, так как координаты точки А не удовлетворяют уравнению плоскости .

Теперь найдем координаты нормальных векторов и плоскостей и и проверим выполнение условия коллинеарности векторов и .

В качестве вектора можно взять векторное произведение векторов и . Векторы и имеют координаты и соответственно (при необходимости смотрите статью нахождение координат вектора по координатам точек его начала и конца). Тогда .

Чтобы определить координаты нормального вектора плоскости приведем ее уравнение к общему уравнению плоскости: . Теперь видно, что .

Проверим выполнение условия коллинеарности векторов и .

Так как , то векторы и связаны равенством , то есть, они коллинеарны.

Итак, плоскости и не совпадают, а их нормальные векторы коллинеарны, следовательно, плоскости и параллельны.

Замечание: разобранное необходимое и достаточное условие не очень удобно для доказательства параллельности плоскостей, так как отдельно приходится доказывать, что плоскости не совпадают.

Уравнение плоскости: как составить? Виды уравнений плоскости

В пространстве плоскость можно задавать разными способами (одной точкой и вектором, двумя точками и вектором, тремя точками и др.). Именно с учетом этого уравнение плоскости может иметь различные виды. Также при соблюдении определенных условий плоскости могут быть параллельными, перпендикулярными, пересекающимися и т.д. Об этом и поговорим в данной статье. Мы научимся составлять общее уравнение плоскости и не только.

Нормальный вид уравнения

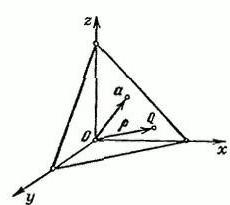
Допустим, есть пространство R₃, которое имеет прямоугольную координатную систему XYZ. Зададим вектор α, который будет выпущен из начальной точки О. Через конец вектора α проведем плоскость П, которая будет ему перпендикулярна.

Обозначим на П произвольную точку Q=(х,у,z). Радиус-вектор точки Q подпишем буквой р. При этом длина вектора α равняется р=IαI и Ʋ=(cosα,cosβ,cosγ).

Это единичный вектор, который направлен в сторону, как и вектор α. α, β и γ – это углы, которые образуются между вектором Ʋ и положительными направлениями осей пространства х, у, z соответственно. Проекция какой-либо точки QϵП на вектор Ʋ является постоянной величиной, которая равна р: (р,Ʋ) = р(р≥0).

Указанное уравнение имеет смысл, когда р=0. Единственное, плоскость П в этом случае будет пересекать точку О (α=0), которая является началом координат, и единичный вектор Ʋ, выпущенный из точки О, будет перпендикулярен к П, несмотря на его направление, что означает, что вектор Ʋ определяется с точностью до знака. Предыдущее уравнение является уравнением нашей плоскости П, выраженным в векторной форме. А вот в координатах его вид будет таким:

Р здесь больше или равно 0. Мы нашли уравнение плоскости в пространстве в нормальном виде.

Общее уравнение

Если уравнение в координатах умножим на любое число, которое не равно нулю, получим уравнение, эквивалентное данному, определяющее ту самую плоскость. Оно будет иметь такой вид:

Здесь А, В, С – это числа, одновременно отличные от нуля. Это уравнение именуется как уравнение плоскости общего вида.

Уравнения плоскостей. Частные случаи

Уравнение в общем виде может видоизменяться при наличии дополнительных условий. Рассмотрим некоторые из них.

Предположим, что коэффициент А равен 0. Это означает, что данная плоскость параллельна заданной оси Ох. В этом случае вид уравнения изменится: Ву+Cz+D=0.

Аналогично вид уравнения будет изменяться и при следующих условиях:

• Во-первых, если В=0, то уравнение изменится на Ах+Cz+D=0, что будет свидетельствовать о параллельности к оси Оу.
• Во-вторых, если С=0, то уравнение преобразуется в Ах+Ву+D=0, что будет говорить о параллельности к заданной оси Oz.
• В-третьих, если D=0, уравнение будет выглядеть как Ах+Ву+Cz=0, что будет означать, что плоскость пересекает О (начало координат).
• В-четвертых, если A=B=0, то уравнение изменится на Cz+D=0, что будет доказывать параллельность к Oxy.
• В-пятых, если B=C=0, то уравнение станет Ах+D=0, а это означает, что плоскость к Oyz параллельна.
• В-шестых, если A=C=0, то уравнение приобретет вид Ву+D=0, то есть будет сообщать о параллельности к Oxz.

Вид уравнения в отрезках

В случае когда числа А, В, С, D отличны от нуля, вид уравнения (0) может быть следующим:

в котором а = -D/А, b = -D/В, с = -D/С.

Получаем в итоге уравнение плоскости в отрезках. Стоит отметить, что данная плоскость будет пересекать ось Ох в точке с координатами (а,0,0), Оу – (0,b,0), а Oz – (0,0,с).

С учетом уравнения х/а + у/b + z/с = 1 нетрудно визуально представить размещение плоскости относительно заданной координатной системы.

Координаты нормального вектора

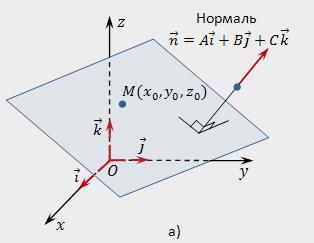
Нормальный вектор n к плоскости П имеет координаты, которые являются коэффициентами общего уравнения данной плоскости, то есть n (А,В,С).

Для того чтобы определить координаты нормали n, достаточно знать общее уравнение заданной плоскости.

При использовании уравнения в отрезках, которое имеет вид х/а + у/b + z/с = 1, как и при использовании общего уравнения, можно записать координаты любого нормального вектора заданной плоскости: (1/а + 1/b + 1/с).

Стоит отметить, что нормальный вектор помогает решить разнообразные задачи. К самым распространенным относятся задачи, заключающиеся в доказательстве перпендикулярности или параллельности плоскостей, задачи по нахождению углов между плоскостями или углов между плоскостями и прямыми.

Вид уравнения плоскости согласно координатам точки и нормального вектора

Ненулевой вектор n, перпендикулярный заданной плоскости, называют нормальным (нормалью) для заданной плоскости.

Предположим, что в координатном пространстве (прямоугольной координатной системе) Oxyz заданы:

• точка Мₒ с координатами (хₒ,уₒ,zₒ);
• нулевой вектор n=А*i+В*j+С*k.

Нужно составить уравнение плоскости, которая будет проходить через точку Мₒ перпендикулярно нормали n.

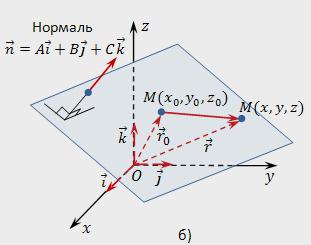
В пространстве выберем любую произвольную точку и обозначим ее М (х у,z). Пускай радиус-вектор всякой точки М (х,у,z) будет r=х*i+у*j+z*k, а радиус-вектор точки Мₒ (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. Точка М будет принадлежать заданной плоскости, если вектор МₒМ будет перпендикулярен вектору n. Запишем условие ортогональности при помощи скалярного произведения:

Поскольку МₒМ = r–rₒ, векторное уравнение плоскости выглядеть будет так:

Данное уравнение может иметь и другую форму. Для этого используются свойства скалярного произведения, а преобразовывается левая сторона уравнения. [r – rₒ, n] = [r, n] – [rₒ, n]. Если [rₒ, n] обозначить как с, то получится следующее уравнение: [r, n] – с = 0 или [r, n] = с, которое выражает постоянство проекций на нормальный вектор радиус-векторов заданных точек, которые принадлежат плоскости.

Теперь можно получить координатный вид записи векторного уравнения нашей плоскости [r – rₒ, n] = 0. Поскольку r–rₒ = (х–хₒ)*i + (у–уₒ)*j + (z–zₒ)*k, а n = А*i+В*j+С*k, мы имеем:

Выходит, у нас образовывается уравнение плоскости, проходящей через точку перпендикулярно нормали n:

Вид уравнения плоскости согласно координатам двух точек и вектора, коллинеарного плоскости

Зададим две произвольные точки М′ (х′,у′,z′) и М″ (х″,у″,z″), а также вектор а (а′,а″,а‴).

Теперь мы сможем составить уравнение заданной плоскости, которая будет проходить через имеющиеся точки М′ и М″, а также всякую точку М с координатами (х,у,z) параллельно заданному вектору а.

При этом векторы М′М= <х-х′;у-у′;z-z′>и М″М= <х″-х′;у″-у′;z″-z′>должны быть компланарными с вектором а=(а′,а″,а‴), а это значит, что (М′М, М″М, а)=0.

Итак, наше уравнение плоскости в пространстве будет выглядеть так:

Вид уравнения плоскости, пересекающей три точки

Допустим, у нас есть три точки: (х′,у′,z′), (х″,у″,z″), (х‴,у‴,z‴), которые не принадлежат одной прямой. Необходимо написать уравнение плоскости, проходящей через заданные три точки. Теория геометрии утверждает, что такого рода плоскость действительно существует, вот только она единственная и неповторимая. Поскольку эта плоскость пересекает точку (х′,у′,z′), вид ее уравнения будет следующим:

Здесь А, В, С отличные от нуля одновременно. Также заданная плоскость пересекает еще две точки: (х″,у″,z″) и (х‴,у‴,z‴). В связи с этим должны выполняться такого рода условия:

Сейчас мы можем составить однородную систему уравнений (линейную) с неизвестными u, v, w:

В нашем случае х,у или z выступает произвольной точкой, которая удовлетворяет уравнение (1). Учитывая уравнение (1) и систему из уравнений (2) и (3), системе уравнений, указанной на рисунке выше, удовлетворяет вектор N (А,В,С), который является нетривиальным. Именно потому определитель данной системы равняется нулю.

Уравнение (1), которое у нас получилось, это и есть уравнение плоскости. Через 3 точки она точно проходит, и это легко проверить. Для этого нужно разложить наш определитель по элементам, находящимся в первой строке. Из существующих свойств определителя вытекает, что наша плоскость одновременно пересекает три изначально заданные точки (х′,у′,z′), (х″,у″,z″), (х‴,у‴,z‴). То есть мы решили поставленную перед нами задачу.

Двухгранный угол между плоскостями

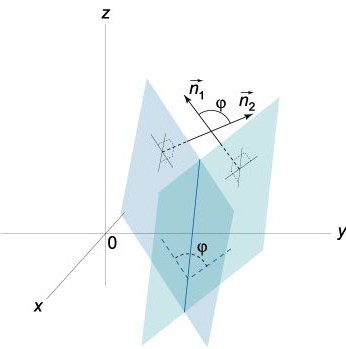
Двухгранный угол представляет собой пространственную геометрическую фигуру, образованную двумя полуплоскостями, которые исходят из одной прямой. Иными словами, это часть пространства, которая ограничивается данными полуплоскостями.

Допустим, у нас имеются две плоскости со следующими уравнениями:

Нам известно, что векторы N=(А,В,С) и N¹=(А¹,В¹,С¹) перпендикулярны согласно заданным плоскостям. В связи с этим угол φ меж векторами N и N¹ равняется углу (двухгранному), который находится между этими плоскостями. Скалярное произведение имеет вид:

Достаточно учесть, что 0≤φ≤π.

На самом деле две плоскости, которые пересекаются, образуют два угла (двухгранных): φ₁ и φ₂. Сумма их равна π (φ₁+ φ₂= π). Что касается их косинусов, то их абсолютные величины равны, но различаются они знаками, то есть cos φ₁=-cos φ₂. Если в уравнении (0) заменить А, В и С на числа -А, -В и -С соответственно, то уравнение, которое мы получим, будет определять эту же плоскость, единственное, угол φ в уравнении cos φ= NN 1 /|N||N 1 | будет заменен на π-φ.

Уравнение перпендикулярной плоскости

Перпендикулярными называются плоскости, между которыми угол равен 90 градусов. Используя материал, изложенный выше, мы можем найти уравнение плоскости, перпендикулярной другой. Допустим, у нас имеются две плоскости: Ах+Ву+Cz+D=0 и А¹х+В¹у+С¹z+D=0. Мы можем утверждать, что перпендикулярными они будут, если cosφ=0. Это значит, что NN¹=АА¹+ВВ¹+СС¹=0.

Уравнение параллельной плоскости

Параллельными называются две плоскости, которые не содержат общих точек.

Условие параллельности плоскостей (их уравнения те же, что и в предыдущем пункте) заключается в том, что векторы N и N¹, которые к ним перпендикулярны, коллинеарные. А это значит, что выполняются следующие условия пропорциональности:

Если условия пропорциональности являются расширенными — А/А¹=В/В¹=С/С¹=DD¹,

это свидетельствует о том, что данные плоскости совпадают. А это значит, что уравнения Ах+Ву+Cz+D=0 и А¹х+В¹у+С¹z+D¹=0 описывают одну плоскость.

Расстояние до плоскости от точки

Допустим, у нас есть плоскость П, которая задана уравнением (0). Необходимо найти до нее расстояние от точки с координатами (хₒ,уₒ,zₒ)=Qₒ. Чтобы это сделать, нужно привести уравнение плоскости П в нормальный вид:

В данном случае ρ (х,у,z) является радиус-вектором нашей точки Q, расположенной на П, р – это длина перпендикуляра П, который был выпущен из нулевой точки, v – это единичный вектор, который расположен в направлении а.

Разница ρ-ρº радиус-вектора какой-нибудь точки Q=(х,у,z), принадлежащий П, а также радиус-вектора заданной точки Q₀=(хₒ,уₒ,zₒ) является таким вектором, абсолютная величина проекции которого на v равняется расстоянию d, которое нужно найти от Q₀=(хₒ,уₒ,zₒ) до П:

(ρ-ρ 0 ,v)= (ρ,v)–(ρ 0 ,v) =р–(ρ 0 ,v).

Вот и получается,

Теперь видно, чтобы рассчитать расстояние d от Q₀ до плоскости П, нужно использовать нормальный вид уравнения плоскости, при этом перенести в левую часть р, а в последнюю вместо х,у,z подставить (хₒ,уₒ,zₒ).

Таким образом, мы найдем абсолютное значение полученного выражения, то есть искомое d.

Используя язык параметров, получаем очевидное:

Если заданная точка Q₀ находится по другую сторону от плоскости П, как и начало координат, то между вектором ρ-ρ 0 и v находится тупой угол, следовательно:

В случае когда точка Q₀ совместно с началом координат располагается по одну и ту же сторону от П, то создаваемый угол острый, то есть:

d=(ρ-ρ 0 ,v)=р — (ρ 0 , v)>0.

В итоге получается, что в первом случае (ρ 0 ,v)>р, во втором (ρ 0 ,v) 2 сентября, 2014

Параллельные плоскости, признак и условия параллельности плоскостей

В данной статье будут изучены вопросы параллельности плоскостей. Дадим определение плоскостям, которые параллельны между собой; обозначим признаки и достаточные условия параллельности; рассмотрим теорию на иллюстрациях и практических примерах.

Параллельные плоскости: основные сведения

Параллельные плоскости – плоскости, не имеющие общих точек.

Чтобы обозначить параллельность применяют такой символ: ∥ . Если заданы две плоскости: α и β , являющиеся параллельными, краткая запись об этом будет выглядеть так: α ‖ β .

На чертеже, как правило, плоскости, параллельные друг другу, отображаются как два равных параллелограмма, имеющих смещение относительно друг друга.

В речи параллельность можно обозначить так: плоскости α и β параллельны, а также – плоскость α параллельна плоскости β или плоскость β параллельна плоскости α .

Параллельность плоскостей: признак и условия параллельности

В процессе решения геометрических задач зачастую возникает вопрос: а параллельны ли заданные плоскости между собой? Для получения ответа на этот вопрос используют признак параллельности, который также является достаточным условием параллельности плоскостей. Запишем его как теорему.

Плоскости являются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Доказательство этой теоремы приводится в программе геометрии за 10 — 11 класс.

В практике для доказательства параллельности, в том числе, применяют две следующие теоремы.

Если одна из параллельных плоскостей параллельна третьей плоскости, то другая плоскость или также параллельна этой плоскости, или совпадает с ней.

Если две несовпадающие плоскости перпендикулярны некоторой прямой, то они параллельны.

На основе этих теорем и самого признака параллельности доказывается факт параллельности любых двух плоскостей.

Рассмотрим подробнее необходимое и достаточное условие параллельности плоскостей α и β , заданных в прямоугольной системе координат трехмерного пространства.

Допустим, что в некоторой прямоугольной системе координат задана плоскость α, которой соответствует общее уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а также задана плоскость β , которую определяет общее уравнение вида A 2 x + B 2 y + C 2 z + D 2 = 0 .

Для параллельности заданных плоскостей α и β необходимо и достаточно, чтобы система линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имела решения (являлась несовместной).

Предположим, что заданные плоскости, определяемые уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 являются параллельными, а значит не имеют общих точек. Таким образом, не существует ни одной точки в прямоугольной системе координат трехмерного пространства, координаты которой отвечали бы условиям одновременно обоих уравнений плоскостей, т.е. система A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 не имеет решения. Если указанная система не имеет решений, тогда не существует ни одной точки в прямоугольной системе координат трехмерного пространства, чьи координаты одновременно отвечали бы условиям обоих уравнений системы. Следовательно, плоскости, заданные уравнениями A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 не имеют ни одной общей точки, т.е. они параллельны.

Разберем использование необходимого и достаточного условия параллельности плоскостей.

Заданы две плоскости: 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 . Необходимо определить, являются ли они параллельными.

Решение

Запишем систему уравнений из заданных условий:

2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Проверим, возможно ли решить полученную систему линейных уравнений.

Ранг матрицы 2 3 1 2 3 1 1 3 равен одному, поскольку миноры второго порядка равны нулю. Ранг матрицы 2 3 1 1 2 3 1 1 3 — 4 равен двум, поскольку минор 2 1 2 3 — 4 отличен от нуля. Таким образом, ранг основной матрицы системы уравнений меньше, чем ранг расширенной матрицы системы.

Совместно с этим, из теоремы Кронекера-Капелли следует: система уравнений 2 x + 3 y + z — 1 = 0 2 3 x + y + 1 3 z + 4 = 0 не имеет решений. Этим фактом доказывается, что плоскости 2 x + 3 y + z — 1 = 0 и 2 3 x + y + 1 3 z + 4 = 0 являются параллельными.

Отметим, что, если бы мы применили для решения системы линейных уравнений метод Гаусса, это дало бы тот же результат.

Ответ: заданные плоскости параллельны.

Необходимое и достаточное условие параллельности плоскостей возможно описать по-другому.

Чтобы две несовпадающие плоскости α и β были параллельны друг другу необходимо и достаточно, чтобы нормальные векторы плоскостей α и β являлись коллинеарными.

Доказательство сформулированного условия базируется на определении нормального вектора плоскости.

Допустим, что n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) являются нормальными векторами плоскостей α и β соответственно. Запишем условие коллинеарности данных векторов:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2 , где t – некое действительное число.

Таким образом, чтобы несовпадающие плоскости α и β с заданными выше нормальными векторами были параллельны, необходимо и достаточно, чтобы имело место действительное число t , для которого верно равенство:

n 1 → = t · n 2 ⇀ ⇔ A 1 = t · A 2 B 1 = t · B 2 C 1 = t · C 2

В прямоугольной системе координат трехмерного пространства заданы плоскости α и β . Плоскость α проходит через точки: A ( 0 , 1 , 0 ) , B ( — 3 , 1 , 1 ) , C ( — 2 , 2 , — 2 ) . Плоскость β описывается уравнением x 12 + y 3 2 + z 4 = 1 Необходимо доказать параллельность заданных плоскостей.

Решение

Удостоверимся, что заданные плоскости не совпадают. Действительно, так и есть, поскольку координаты точки A не соответствуют уравнению плоскости β .

Следующим шагом определим координаты нормальных векторов n 1 → и n 2 → , соответствующие плоскостям α и β . Также проверим условие коллинеарности этих векторов.

Вектор n 1 → можно задать, взяв векторное произведение векторов A B → и A C → . Их координаты соответственно: ( — 3 , 0 , 1 ) и ( — 2 , 2 , — 2 ) . Тогда:

n 1 → = A B → × A C → = i → j → k → — 3 0 1 — 2 1 — 2 = — i → — 8 j → — 3 k → ⇔ n 1 → = ( — 1 , — 8 , — 3 )

Для получения координат нормального вектора плоскости x 12 + y 3 2 + z 4 = 1 приведем это уравнение к общему уравнению плоскости:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z — 1 = 0

Таким образом: n 2 → = 1 12 , 2 3 , 1 4 .

Осуществим проверку, выполняется ли условие коллинеарности векторов n 1 → = ( — 1 , — 8 , — 3 ) и n 2 → = 1 12 , 2 3 , 1 4

Так как — 1 = t · 1 12 — 8 = t · 2 3 — 3 = t · 1 4 ⇔ t = — 12 , то векторы n 1 → и n 2 → связаны равенством n 1 → = — 12 · n 2 → , т.е. являются коллинеарными.

Ответ: плоскости α и β не совпадают; их нормальные векторы коллинеарные. Таким образом, плоскости α и β параллельны.