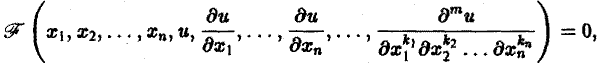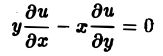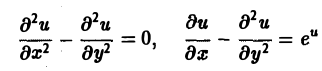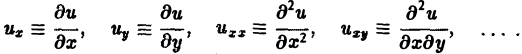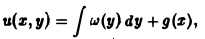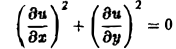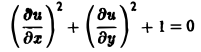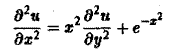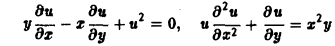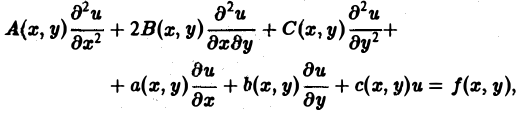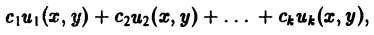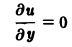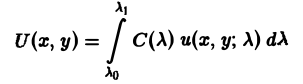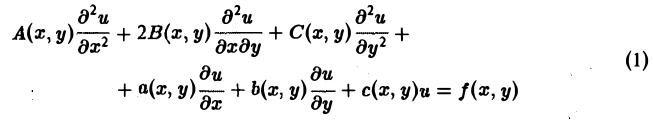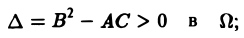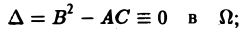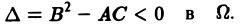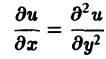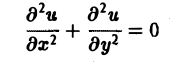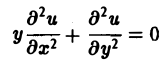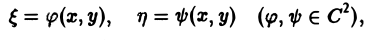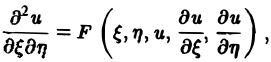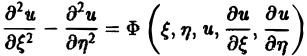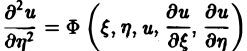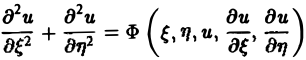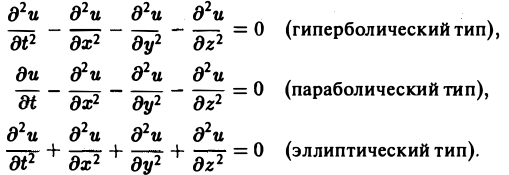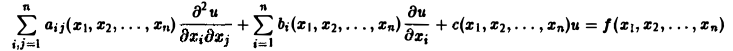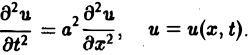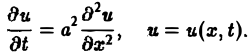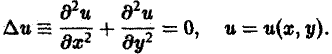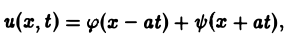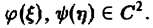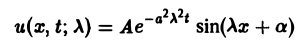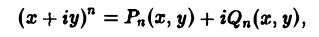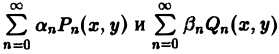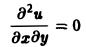Уравнения второго порядка относительно производной

РАЗРЕШЕНИЕ АЛГЕБРО-ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Усков Владимир Игоревич

В статье рассматривается алгебро-дифференциальное уравнение второго порядка . Уравнениями и системами дифференциальных уравнений второго порядка описывается работа схемы электронного триода с обратной связью, вращение жесткого тела с полостью, считывание информации с диска и т. д. Перед старшей производной находится необратимый оператор. Этот оператор фредгольмов с нулевым индексом, обладающий ядром произвольной размерности и цепочками Жордана произвольной длины. Уравнения с необратимыми операторами при старшей производной называются алгебродифференциальными. В связи с этим решение задачи существует при определенных условиях на компоненты искомой функции. Для разрешения уравнения относительно производной применяется метод каскадной декомпозиции уравнения, заключающегося в пошаговом расщеплении уравнения на уравнения в подпространствах уменьшающихся размерностей. Рассмотрены случаи одношагового и двухшагового расщепления. При расщеплении используется результат о решении линейного уравнения с фредгольмовым оператором. В каждом случае получен результат, сформулированный в виде теоремы. Для иллюстрации полученного результата в случае одношагового расщепления приводится иллюстрирующий пример задачи Коши .

Похожие темы научных работ по математике , автор научной работы — Усков Владимир Игоревич

SOLVING A SECOND-ORDER ALGEBRO-DIFFERENTIAL EQUATION WITH RESPECT TO THE DERIVATIVE

We consider a second-order algebro-differential equation. Equations and systems of second-order differential equations describe the operation of an electronic triode circuit with feedback, rotation of a rigid body with a cavity, reading information from a disk, etc. The highest derivative is preceded by an irreversible operator. This is a Fredholm operator with index zero, kernel of arbitrary dimension, and Jordan chains of arbitrary lengths. Equations with irreversible operators at the highest derivative are called algebro-differential. In this case, the solution to the problem exists under certain conditions on the components of the desired function. To solve the equation with respect to the derivative, the method of cascade splitting of the equation is used, which consists in the stepwise splitting of the equation into equations in subspaces of decreasing dimensions. Cases of one-step and two-step splitting are considered. The splitting uses the result on the solution of a linear equation with Fredholm operator. In each case, the corresponding result is formulated as a theorem. To illustrate the result obtained in the case of one-step splitting, an illustrative example of the Cauchy problem is given.

Текст научной работы на тему «РАЗРЕШЕНИЕ АЛГЕБРО-ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ВТОРОГО ПОРЯДКА ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ»

DOI 10.20310/2686-9667-2021-26-136-414-420 УДК 517.922

open fil access

Разрешение алгебро-дифференциального уравнения второго порядка относительно производной

Владимир Игоревич УСКОВ

ФГБОУ ВО «Воронежский государственный лесотехнический университет имени Г. Ф. Морозова» 394613, Российская Федерация, г. Воронеж, ул. Тимирязева, 8

Аннотация. В статье рассматривается алгебро-дифференциальное уравнение второго порядка. Уравнениями и системами дифференциальных уравнений второго порядка описывается работа схемы электронного триода с обратной связью, вращение жесткого тела с полостью, считывание информации с диска и т. д. Перед старшей производной находится необратимый оператор. Этот оператор фредгольмов с нулевым индексом, обладающий ядром произвольной размерности и цепочками Жордана произвольной длины. Уравнения с необратимыми операторами при старшей производной называются алгебро-дифференциальными. В связи с этим решение задачи существует при определенных условиях на компоненты искомой функции. Для разрешения уравнения относительно производной применяется метод каскадной декомпозиции уравнения, заключающегося в пошаговом расщеплении уравнения на уравнения в подпространствах уменьшающихся размерностей. Рассмотрены случаи одношагового и двухшагового расщепления. При расщеплении используется результат о решении линейного уравнения с фредгольмовым оператором. В каждом случае получен результат, сформулированный в виде теоремы. Для иллюстрации полученного результата в случае одношагового расщепления приводится иллюстрирующий пример задачи Коши.

Ключевые слова: алгебро-дифференциальное уравнение второго порядка, банахово пространство, фредгольмов оператор, каскадная декомпозиция, задача Коши

Для цитирования: Усков В.И. Разрешение алгебро-дифференциального уравнения второго порядка относительно производной // Вестник российских университетов. Математика. 2021. Т. 26. № 136. С. 414-420. БО! 10.20310/2686-9667-2021-26-136-414-420.

Solving a second-order algebro-differential equation with respect to the derivative

Vladimir I. USKOV

Voronezh State University of Forestry and Technologies after named G.F. Morozov 8 Timiryazeva St., Voronezh 394613, Russian Federation

Abstract. We consider a second-order algebro-differential equation. Equations and systems of second-order differential equations describe the operation of an electronic triode circuit with feedback, rotation of a rigid body with a cavity, reading information from a disk, etc. The highest derivative is preceded by an irreversible operator. This is a Fredholm operator with index zero, kernel of arbitrary dimension, and Jordan chains of arbitrary lengths. Equations with irreversible operators at the highest derivative are called algebro-differential. In this case, the solution to the problem exists under certain conditions on the components of the desired function. To solve the equation with respect to the derivative, the method of cascade splitting of the equation is used, which consists in the stepwise splitting of the equation into equations in subspaces of decreasing dimensions. Cases of one-step and two-step splitting are considered. The splitting uses the result on the solution of a linear equation with Fredholm operator. In each case, the corresponding result is formulated as a theorem. To illustrate the result obtained in the case of one-step splitting, an illustrative example of the Cauchy problem is given.

Keywords: second-order algebro-differential equation, Banach space, Fredholm operator, cascade splitting, Cauchy problem

Mathematics Subject Classification: 34A12.

For citation: Uskov V.I. Razresheniye algebro-differentsial’nogo uravneniya vtorogo poryadka otnositel’no proizvodnoy [Solving a second-order algebro-differential equation with respect to the derivative]. Vestnik rossiyskikh universitetov. Matematika — Russian Universities Reports. Mathematics, 2021, vol. 26, no. 136, pp. 414-420. DOI 10.20310/2686-9667-2021-26-136-414-420. (In Russian, Abstr. in Engl.)

Уравнениями и системами дифференциальных уравнений второго порядка описывается работа схемы электронного триода с обратной связью (уравнение Рэлея) [1], вращение жесткого тела с полостью (уравнение Ламе) [2], считывание информации с диска [3] и т. д.

Уравнения с вырожденным оператором при старшей производной называют алгебро-дифференциальными. Задача Коши решалась в работе [4], где этот оператор — нормально разрешимый фредгольмов с и -мерным ядром, имеющий относительно некоторой оператор-функции полный биканонический жорданов набор; в работе [5] операторные коэффициенты являются и х и -матрицами, для краевой задачи применялся метод сеток. Используемый здесь метод каскадной декомпозиции применялся в работе [6] при исследовании возмущений, вызываемых наличием малого параметра у алгебро-дифференциального уравнения первого порядка.

В настоящей работе рассматривается уравнение

где Л, В : Е ^ Е2 — замкнутые линейные операторы, Е^Е — банаховы пространства, ёош Л = Е, ёош В = Е ; Л — фредгольмов оператор с нулевым индексом; Е(Г) — заданная функция со значениями в Е2.

Здесь оператор Л имеет более сложную структуру — каждый элемент ядра имеет присоединенные элементы различной длины.

Фредгольмов оператор Л вполне определяется следующими свойствами. Свойство А (см. [7]).

Е1 = Сот Л ф Кег Л, Е2 = 1ш Л ф Сокег Л,

где Сот Л —прямое дополнение к Кег Л в Е1 , Сокег Л —дефектное подпространство, Кег Л = Сокег Л Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

и(г)= | и2(г) | € R3 — искомая функция, и0 :=и(0):

начальные векторы, F(г) = 0. Для оператора А имеем:

Дифференциальные уравнения в частных производных с примерами решения и образцами выполнения

Дифференциальным уравнением с частными производными называется уравнение вида
(1)

связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.

Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то

— дифференциальное уравнение 1-го порядка;

— дифференциальные уравнения 2-го порядка.

Для упрощения записи пользуются также следующими обозначениями:

Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через С m (D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.

Определение:

Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ С m (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.

Пример:

Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,

u = φ(y). (3)

Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).

Приме:

Найти решение u = u(z, у) уравнения

Положим = о. Тогда уравнение (4) примет вид = 0. Его общим решением будет произвольная функция v = w(у). Поскольку v= приходим к уравнению = w(у). Интегрируя по у (считая х параметром), получим

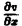
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде

u(x, y) = f(y) + g(x) (5)

произвольные дифференцируемые функции).

Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.

Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.

Пример:

Множество действительных решений уравнения

исчерпывается функцией u(x, y) = const, а уравнение

вовсе не имеет действительных решений.

Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.

Линейные дифференциальные уравнения с частными производными. Свойства их решений

Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.

Пример:

— линейное уравнение; уравнения

Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)

где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.

Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде

L[u] = f(x, у). (2)

Соответствующее однородное уравнение запишется так:

L[u] = 0. (3)

Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C 2 (D) функций и = и(х, у).

Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.

Теорема:

Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).

Теорема:

Если и₁(х, у) и и₂(х, у) — решения линейного однородного уравнения (3), то сумма и₁(х, у) + и₂(x, у) есть также решение этого уравнения.

Следствие:

Если каждая из функций и₁(х, у) и и₂(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация

где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.

В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная

комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.

Пример:

имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, х n ,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 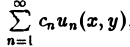, членами которых являются произведения постоянных Сп на частные решения иn(х, у) дифференциального уравнения.

Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла

по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения

L[u] = f (4)

справедливы следующие предложения.

Теорема:

Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).

Теорема:

Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.

Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными

Определение:

Линейное дифференциальное уравнение второго порядка

в некоторой области Q на плоскости хОу называется

1) гиперболическим в Ω, если

2) параболическим в Ω, если

3) эллиптическим в Ω, если

Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение

— параболическое при всех х и у, а уравнение

— эллиптическое при всех х и у. Уравнение

— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у

с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.

Уравнение гиперболического типа (∆ > 0) преобразуется к вшу

(два канонических вида уравнений гиперболического типа).

Уравнение параболического типа (∆ ≡ 0) преобразуется к виду

(канонический вид уравнения параболического типа).

Уравнение эллиптического типа (∆

(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 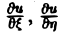и независимых переменных ξ, η. Вид функций F и Ф определяется исходным уравнением (1).

В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.

Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).

Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид

Здесь и = и(х, у, z, t).

Замечание:

В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами

к каноническому виду возможно только в данной точке 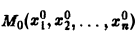и невозможно в любой сколь угодно малой окрестности этой точки.

Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.

Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)

Здесь х — пространственная координата, t — время, 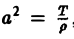где Т — натяжение струны, р — ее линейная плотность.

Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)

Здесь 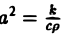где р — плотность среды, с — удельная теплоемкость, k — коэффициент теплопроводности.

Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)

Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида

Можно показать, что решениями уравнения (3) являются функции вида

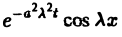
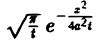
произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = уравнения (3) по параметру λ в пределах от — ∞ до + ∞ , получим так называемое фундаментальное решение U(x, t) = уравнения теплопроводности.

Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения

являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции

f(z) = u(x, у) + iv(x, у)

комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).

В силу линейности уравнения (4) ряды

тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.

Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.

Постановка основных задач для линейных дифференциальных уравнений второго порядка

Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.

Пример:

Общее решение уравнения

имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.

Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):

а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством R n , граничные условия отсутствуют;

б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;

в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ R n

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Лекция по высшей математике»Дифференциальные уравнения второго порядка»(для 26 гр.)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА

1) ОСНОВНЫЕ ПОНЯТИЯ

Дифференциальным уравнением второго порядка называется уравнение, содержащее неизвестную (искомую) функцию у(х) , независимую переменную х , первую и вторую производные у’, у» или дифференциалы

Дифференциальное уравнение второго порядка символически можно записать в общем виде следующим образом:

Дифференциальное уравнение второго порядка, разрешенное относительно второй производной, имеет вид:

Решением дифференциального уравнения называется всякая функция, которая обращает его в тождество. Дифференциальное уравнение второго порядка имеет бесчисленное множество решений, которые можно представить в виде функции Эта совокупность решений называется общим решением .

Функция, получающаяся из общего решения при конкретных значениях постоянных С ₁ и С ₂ , называется частным решением . Частное решение находится при помощи задания начальных условий: у(х=х ₀ )=у ₀ и у'(х=х ₀ )=у ₀ ‘ , где х ₀ , у ₀ , у ₀ ‘ – конкретные числа.

Задача отыскания частного решения дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши . Практически задачу Коши решают следующим образом: находят общее решение, затем в него подставляют начальные условия, получают систему двух уравнений, определяют произвольные постоянные С ₁ и С ₂ и подставляют их конкретные значения в общее решение.

2) ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО

ПОРЯДКА, ДОПУСКАЮЩИЕ ПОНИЖЕНИЕ ПОРЯДКА

Рассмотрим некоторые типы дифференциальных уравнений второго порядка, которые позволяют понизить порядок уравнения и привести его к уравнениям первого порядка.

2.1. Дифференциальное уравнение вида

Правая часть уравнения не содержит у и у’ . Уравнение решается путем последовательного интегрирования. Найдем сначала первую производную (промежуточное общее решение):

Интегрируя еще раз, получим общее решение:

Пример 1. Найти частное решение уравнения при заданных начальных условиях у(х= 0 )= 1 и у'(х= 0 )= 1.

Решение. Последовательно интегрируя, найдем сначала первую производную (промежуточное общее решение):

Интегрируя еще раз, получим общее решение:

Так как мы интегрировали дважды, то получили две произвольные постоянные С ₁ и С ₂ . Подставляя начальные условия в соотношения (2.1) и (2.2), получим С ₁ =1 и С ₂ =1. Следовательно, частное решение имеет вид:

2.2. Дифференциальное уравнение вида

Правая часть уравнения не содержит искомой функции у . Уравнение решается с помощью подстановки:

где z – функция от х . Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка: .

Решая это уравнение, найдем общее решение в виде Делая обратную замену получим еще одно дифференциальное уравнение первого порядка:

Разделяя переменные и интегрируя, получим общее решение

Пример 2. Найти общее решение уравнения

Решение. Сделаем подстановку: Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

Разделяем переменные: Интегрируем:

Получаем промежуточное общее решение: или

Делая обратную замену получим еще одно дифференциальное уравнение первого порядка с разделяющимися переменными: или

Интегрируя, получим общее решение:

Пример 3. Найти общее решение уравнения

Решение. Сделаем подстановку: Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

Уравнение (2.3) является однородным и решается с помощью подстановки:

Подставляя (2.4) в (2.3), получим дифференциальное уравнение с разделяющимися переменными:

Сокращаем на х и разделяем переменные:

Интеграл в левой части равенства (2.5) вычисляем методом замены переменной:

После интегрирования (2.5) получаем промежуточное общее решение:

Делая обратную замену получим дифференциальное уравнение первого порядка с разделяющимися переменными: или .

Разделяем переменные и интегрируем: (2.6)

Интеграл, стоящий в правой части, вычисляем с помощью формулы интегрирования по частям:

После интегрирования (2.6) получим общее решение:

Пример 4. Найти общее решение уравнения

Решение. Сделаем подстановку: Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

Уравнение (2.7) является линейным неоднородным и решается с помощью подстановки:

Подставляя (2.8) в (2.7), получим:

Квадратную скобку приравняем к нулю и решим полученное уравнение с разделяющимися переменными:

Разделяем переменные и интегрируем: Получаем: или

Функцию подставляем в соотношение (2.9):

Сокращаем на х , разделяем переменные и интегрируем:

Делая обратную замену получим дифференциальное уравнение первого порядка с разделяющимися переменными: или

Разделяем переменные и интегрируем:

Интеграл, стоящий в правой части (2.10), вычисляем с помощью формулы интегрирования по частям:

После интегрирования (2.10) получим общее решение:

2.3. Дифференциальное уравнение вида

Правая часть уравнения не содержит независимой переменной х . Уравнение решается с помощью подстановки: или

где z – функция от у , т.е. z = z [ y ( x )] – сложная функция от х . Тогда :

Исходное уравнение преобразуется в дифференциальное уравнение первого порядка:

где z – искомая функция, у – независимая переменная.

Решая это уравнение, найдем общее решение в виде Делая обратную замену получим еще одно дифференциальное уравнение первого порядка:

Разделяя переменные и интегрируя, получим общее решение

Пример 5. Найти общее решение уравнения

Решение. Сделаем подстановку:

Тогда исходное уравнение преобразуется в дифференциальное уравнение первого порядка с разделяющимися переменными:

Сокращаем на z ( z ≠0) и разделяем переменные:

Получаем промежуточное общее решение: или

Делая обратную замену получим еще одно дифференциальное уравнение первого порядка с разделяющимися переменными:

Разделяем переменные: Интегрируя, получим общее решение:

3) Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Линейные однородные дифференциальные уравнения.

Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида , (1)

т.е. уравнение, которое содержит искомую функцию и её производные только в первой степени и не содержит их произведений. В этом уравнении и — некоторые числа, а функция задана на некотором интервале .

Если на интервале , то уравнение (1) примет вид , (2)

и называется линейным однородным . В противном случае уравнение (1) называется линейным неоднородным . Рассмотрим комплексную функцию , (3)

где и — действительные функции. Если функция (3) является комплексным решением уравнения (2), то и действительная часть , и мнимая часть решения в отдельности являются решениями этого же однородного уравнения. Таким образом, всякое комплексное решение уравнения (2) порождает два действительных решения этого уравнения.

Решения однородного линейного уравнения обладают свойствами:

Если есть решение уравнения (2), то и функция , где С – произвольная постоянная, также будет решением уравнения (2);

Если и есть решения уравнения (2), то и функция также будет решением уравнения (2);

Если и есть решения уравнения (2), то их линейная комбинация также будет решением уравнения (2), где и – произвольные постоянные.

Функции и называются линейно зависимыми на интервале , если существуют такие числа и , не равные нулю одновременно, что на этом интервале выполняется равенство

Если равенство (4) имеет место только тогда, когда и , то функции и называются линейно независимыми на интервале .

Пример 1 . Функции и линейно зависимы, так как на всей числовой прямой. В этом примере .

Пример 2 . Функции и линейно независимы на любом интервале, т. к. равенство возможно лишь в случае, когда и , и .

Построение общего решения линейного однородного уравнения.

Для того, чтобы найти общее решение уравнения (2), нужно найти два его линейно независимых решения и . Линейная комбинация этих решений , где и – произвольные постоянные, и даст общее решение линейного однородного уравнения. Линейно независимые решения уравнения (2) будем искать

в виде , (5) ,где – некоторое число. Тогда , . Подставим эти выражения в уравнение (2):

Так как , то . Таким образом, функция будет решением уравнения (2), если будет удовлетворять уравнению . (6)

Уравнение (6) называется характеристическим уравнением для уравнения (2). Это уравнение является алгебраическим квадратным уравнением.

Пусть и есть корни этого уравнения. Они могут быть или действительными и различными, или комплексными, или действительными и равными. Рассмотрим эти случаи.

Пусть корни и характеристического уравнения действительные и различны. Тогда решениями уравнения (2) будут функции и . Эти решения линейно независимы, так как равенство может выполняться лишь тогда, когда и , и . Поэтому общее решение уравнения (2) имеет вид , где и — произвольные постоянные.

Пример 3 . Найти общее решение дифференциального уравнения .

Решение . Характеристическим уравнением для данного дифференциального будет . Решив это квадратное уравнение, найдём его корни и . Функции и являются решениями дифференциального уравнения. Общее решение этого уравнения имеет вид .

Комплексным числом называется выражение вида , где и — действительные числа, а называется мнимой единицей. Если , то число называется чисто мнимым. Если же , то число отождествляется с действительным числом .

Число называется действительной частью комплексного числа, а — мнимой частью. Если два комплексных числа отличаются друг от друга только знаком мнимой части, то они зазываются сопряжёнными: ,

Пример 4 . Решить квадратное уравнение .

Решение . Дискриминант уравнения . Тогда . Аналогично, . Таким образом, данное квадратное уравнение имеет сопряжённые комплексные корни.

Пусть корни характеристического уравнения комплексные , т.е. , , где . Решения уравнения (2) можно записать в виде , или , . По формулам Эйлера: , .

Тогда , . Как известно, если комплексная функция является решением лин. одн. ур-я, то решениями этого уравнения являются и действительная, и мнимая части этой функции. Таким образом, решениями уравнения (2) будут функции и . Так как равенство

может выполняться только в том случае, если и , то эти решения линейно независимы. Следовательно, общее решение уравнения (2) имеет вид ,

где и — произвольные постоянные.

Пример 5 . Найти общее решение дифференциального уравнения .

Решение . Уравнение является характеристическим для данного дифференциального. Решим его и получим комплексные корни , . Функции и являются линейно независимыми решениями дифференциального уравнения. Общее решение этого уравнения имеет вид .

Пусть корни характеристического уравнения действительные и равные, т.е. . Тогда решениями уравнения (2) являются функции и . Эти решения линейно независимы, так как выражение может быть тождественно равным нулю только тогда, когда и . Следовательно, общее решение уравнения (2) имеет вид .

Пример 6 . Найти общее решение дифференциального уравнения .

Решение . Характеристическое уравнение имеет равные корни . В этом случае линейно независимыми решениями дифференциального уравнения являются функции и . Общее решение имеет вид .

Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

Общее решение линейного неоднородного уравнения (1) равно сумме общего решения соответствующего однородного уравнения и любого частного решения неоднородного уравнения: .

В некоторых случаях частное решение неоднородного уравнения можно найти довольно просто по виду правой части уравнения (1). Рассмотрим случаи, когда это возможно.

Пусть неоднородное уравнение имеет вид , (7)

т.е. правая часть неоднородного уравнения является многочленом степени m . Если не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде многочлена степени m , т.е. .

Коэффициенты определяются в процессе нахождения частного решения.

Если же является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде .

Пример 7 . Найти общее решение дифференциального уравнения .

Решение . Соответствующим однородным уравнением для данного уравнения является

. Его характеристическое уравнение имеет корни и .

Общее решение однородного уравнения имеет вид .

Так как не является корнем характеристического уравнения, то частное решение неоднородного уравнения будем искать в виде функции . Найдём производные этой функции , и подставим их в данное уравнение :

или . Приравняем коэффициенты при и свободные члены: Решив данную систему , получим , . Тогда частное решение неоднородного уравнения имеет вид , а общим решением данного неоднородного уравнения будет сумма общего решения соответствующего однородного уравнения и частного решения неоднородного:

Пусть неоднородное уравнение имеет вид (8)

Если не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде . Если же есть корень характеристического уравнения кратности k ( k =1 или k =2), то в этом случае частное решение неоднородного уравнения будет иметь вид .

Пример 8 . Найти общее решение дифференциального уравнения .

Решение . Характеристическое уравнение для соответствующего однородного уравнения имеет вид . Его корни , . В этом случае общее решение соответствующего однородного уравнения записывается в виде .

Так как число 3 не является корнем характеристического уравнения, то частное решение неоднородного уравнения следует искать в виде . Найдём производные первого и второго порядков: ,. Подставим в дифференциальное уравнение: +,

Приравняем коэффициенты при и свободные члены:

Тогда частное решение данного уравнения имеет вид , а общее решение