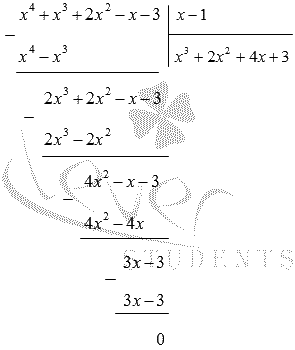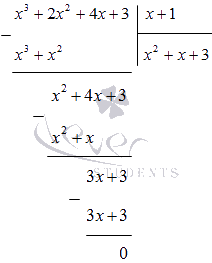Урок алгебры в 10-м классе (занятие элективного курса) по теме «Методы решения уравнений высших степеней»
Презентация к уроку
На занятии изучается методика решения уравнений высших степеней. Рассматриваются два метода: разложение на множители и замена переменной. Понижение степени уравнений с помощью деления многочленов по схеме Горнера и приведение различных уравнений к замене переменной. Дана историческая справка исследования уравнений высших степеней. Представлена презентация урока.
Метод разложения на множители.
Этот метод основан на применении теоремы Безу. Если число α является корнем многочлена P(x) степени n, то его можно представить в виде P(x) = (x — α)Q(x), где Q(x) — многочлен степени (n-1).Теорема Безу: “Остаток от деления многочлена Р(х) на двучлен (x — α) равен P(α), т.е. значению многочлена при x = α” Таким образом, если известен хотя бы один корень уравнения Р(х)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени (n-1), понизить степень уравнения. Теорема. Пусть несократимая дробь p/q является корнем уравнения a0x n + a1x n-1 + . + ax-1x+ an = 0 с целыми коэффициентами, тогда число p – является делителем свободного члена an, а q – делителем старшего коэффициента a0. У многочлена с целыми коэффициентами целые корни являются делителями свободного члена. Таким образом, зная корень многочлена, его легко разложить на множители, т.е. разделить P(x) на (x — α) “углом” или по схеме Горнера.
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Уравнения высших степеней
методическая разработка по алгебре (10 класс) на тему
Рассмотренны шесть различных типов уравнений высших степеней и тексты контрольной работы в четырёх вариантах!
Скачать:
| Вложение | Размер |
|---|---|
| уравнения высших степеней | 101.75 КБ |
Предварительный просмотр:
Подписи к слайдам:
Уравнения высших степеней (корни многочлена от одной переменной).
П лан лекции. № 1 . Уравнения высших степеней в школьном курсе математики. № 2 . Стандартный вид многочлена. № 3 .Целые корни многочлена. Схема Горнера. № 4. Дробные корни многочлена. № 5. Уравнения вида: ( х + а )( х + в )( х + с ) … = А № 6. Возвратные уравнения. № 7. Однородные уравнения. № 8. Метод неопределенных коэффициентов. № 9. Функционально – графический метод. № 10. Формулы Виета для уравнений высших степеней. № 11. Нестандартные методы решения уравнений высших степеней.
Уравнения высших степеней в школьном курсе математики . 7 класс. Стандартный вид многочлена. Действия с многочленами. Разложение многочлена на множители. В обычном классе 42 часа , в спец классе 56 часов. 8 спецкласс . Целые корни многочлена, деление многочленов, возвратные уравнения, разность и сумма п – ых степеней двучлена, метод неопределенных коэффициентов. Ю.Н. Макарычев « Дополнительные главы к школьному курсу алгебры 8 класса», М.Л.Галицкий Сборник задач по алгебре 8 – 9 класс». 9 спецкласс . Рациональные корни многочлена. Обобщенные возвратные уравнения. Формулы Виета для уравнений высших степеней. Н.Я. Виленкин « Алгебра 9 класс с углубленным изучением. 11 спецкласс . Тождественность многочленов. Многочлен от нескольких переменных. Функционально – графический метод решения уравнений высших степеней.
Стандартный вид многочлена. Многочлен Р( х ) = а ⁿ х ⁿ + а п-1 х п-1 + … + а₂х ² + а₁х + а₀. Называется многочленом стандартного вида. а п х ⁿ — старший член многочлена а п — коэффициент при старшем члене многочлена. При а п = 1 Р( х ) называется приведенным многочленом. а ₀ — свободный член многочлена Р( х ). п – степень многочлена.
Целые корни многочлена. Схема Горнера. Теорема № 1. Если целое число а является корнем многочлена Р( х ), то а – делитель свободного члена Р( х ). Пример № 1 . Решите уравнение. Х⁴ + 2х³ = 11х² – 4х – 4 Приведем уравнение к стандартному виду. Х⁴ + 2х³ — 11х² + 4х + 4 = 0. Имеем многочлен Р( х ) = х ⁴ + 2х³ — 11х² + 4х + 4 Делители свободного члена: ± 1, ± 2, ±4. х = 1 корень уравнения т.к. Р(1) = 0, х = 2 корень уравнения т.к. Р(2) = 0 Теорема Безу. Остаток от деления многочлена Р( х ) на двучлен ( х – а) равен Р(а). Следствие. Если а – корень многочлена Р( х ), то Р( х ) делится на ( х – а ). В нашем уравнении Р( х ) делится на ( х – 1) и на ( х – 2), а значит и на ( х – 1) ( х – 2). При делении Р( х ) на ( х ² — 3х + 2) в частном получается трехчлен х ² + 5х + 2 = 0, который имеет корни х =( -5 ± √17)/2
Дробные корни многочлена. Теорема №2. Если р / g корень многочлена Р( х ), то р – делитель свободного члена, g – делитель коэффициента старшего члена Р( х ). Пример № 2. Решите уравнение. 6х³ — 11х² — 2х + 8 = 0. Делители свободного члена: ±1, ±2, ±4, ±8. Ни одно из этих чисел не удовлетворяет уравнению. Целых корней нет. Натуральные делители коэффициента старшего члена Р( х ): 1, 2, 3, 6. Возможные дробные корни уравнения: ±2/3, ±4/3, ±8/3. Проверкой убеждаемся, что Р(4/3) = 0. Х = 4/3 корень уравнения. По схеме Горнера разделим Р( х ) на ( х – 4/3).
Примеры для самостоятельного решения. Решите уравнения: 9х³ — 18х = х – 2, х ³ — х ² = х – 1, х ³ — 3х² -3х + 1 = 0, Х ⁴ — 2х³ + 2х – 1 = 0, Х⁴ — 3х² + 2 = 0, х ⁵ + 5х³ — 6х² = 0, х ³ + 4х² + 5х + 2 = 0, Х⁴ + 4х³ — х ² — 16х – 12 = 0 4х³ + х ² — х + 5 = 0 3х⁴ + 5х³ — 9х² — 9х + 10 = 0. Ответы: 1) ±1/3; 2 2) ±1, 3) -1; 2 ±√3 , 4) ±1, 5) ± 1; ±√2 , 6) 0; 1 7) -2; -1, 8) -3; -1; ±2, 9) – 5/4 10) -2; — 5/3; 1.
Уравнения вида ( х + а)( х + в)( х + с )( х + d )… = А. Пример №3 . Решите уравнение ( х + 1)( х + 2)( х + 3)( х + 4) =24. а = 1, в = 2, с = 3, d = 4 а + d = в + с. Перемножаем первую скобку с четвертой и вторую с третьей. ( х + 1)( х + 4)( х + 20( х + 3) = 24. ( х ² + 5х + 4)( х ² + 5х + 6) = 24. Пусть х ² + 5х + 4 = у, тогда у( у + 2) = 24, у² + 2у – 24 = 0 у₁ = — 6, у₂ = 4. х ² + 5х + 4 = -6 или х ² + 5х + 4 = 4. х ² + 5х + 10 = 0, Д о при х > о. Функция f ( х ) возрастающая при х > о, а значение f (о) = -2. Очевидно, что уравнение имеет один положительный корень ч.т.д. Пример №17. Решите уравнение 8х(2х² — 1)(8х⁴ — 8х² + 1) = 1. И.Ф.Шарыгин « Факультативный курс по математике для 11 класса».М. Просвещение 1991 стр90. 1. l х l 1 2х² — 1 > 1 и 8х⁴ -8х² + 1 > 1 2. Сделаем замену х = cosy , у € (0; п ). При остальных значениях у, значения х повторяются, а уравнение имеет не более 7 корней. 2х² — 1 = 2 cos²y – 1 = cos2y , 8х⁴ — 8х² + 1 = 2(2х² — 1)² — 1 = 2 cos²2y – 1 = cos4y . 3. Уравнение принимает вид 8 cosycos2ycos4y = 1. Умножаем обе части уравнения на siny . 8 sinycosycos2ycos4y = siny . Применяя 3 раза формулу двойного угла получим уравнение sin8y = siny , sin8y – siny = 0
Окончание решения примера №17. Применяем формулу разности синусов. 2 sin7y/2 · cos9y/2 = 0 . Учитывая, что у € (0;п), у = 2пк/3, к = 1, 2, 3 или у = п /9 + 2пк/9, к =0, 1, 2, 3. Возвращаясь к переменной х получаем ответ: Cos2 п /7, cos4 п /7, cos6 п /7, cos п /9, ½, cos5 п /9, cos7 п /9 . Примеры для самостоятельного решения. Найти все значения а, при которых уравнение ( х ² + х )( х ² + 5х + 6) = а имеет ровно три корня. Ответ: 9/16. Указание: построить график левой части уравнения. F max = f(0) = 9/16 . Прямая у = 9/16 пересекает график функции в трех точках. Решите уравнение ( х ² + 2х)² — ( х + 1)² = 55. Ответ: -4; 2. Решите уравнение ( х + 3)⁴ + ( х + 5)⁴ = 16. Ответ: -5; -3. Решите уравнение 2( х ² + х + 1)² -7( х – 1)² = 13( х ³ — 1).Ответ: -1; -1/2, 2;4 Найдите число действительных корней уравнения х ³ — 12х + 10 = 0 на [-3; 3/2]. Указание: найти производную и исследовать на монот .
Примеры для самостоятельного решения ( продолжение). 6. Найдите число действительных корней уравнения х ⁴ — 2х³ + 3/2 = 0. Ответ: 2 7. Пусть х ₁, х ₂, х ₃ — корни многочлена Р( х ) = х ³ — 6х² -15х + 1. Найдите Х₁² + х ₂² + х ₃². Ответ: 66. Указание: примените теорему Виета. 8. Докажите, что при а > о и произвольном вещественном в уравнение х ³ + ах + в = о имеет только один вещественный корень. Указание: проведите доказательство от противного. Примените теорему Виета. 9. Решите уравнение 2( х ² + 2)² = 9( х ³ + 1). Ответ: ½; 1; (3 ± √13)/2. Указание: приведите уравнение к однородному, используя равенства Х² + 2 = х + 1 + х ² — х + 1, х ³ + 1 = ( х + 1)( х ² — х + 1). 10. Решите систему уравнений х + у = х ², 3у – х = у². Ответ: (0;0),(2;2), (√2; 2 — √2), (- √2 ; 2 + √2). 11. Решите систему: 4у² -3ху = 2х –у, 5х² — 3у² = 4х – 2у. Ответ: ( о;о ), (1;1),(297/265; — 27/53).
Контрольная работа. 1 вариант. 1. Решите уравнение ( х ² + х ) – 8( х ² + х ) + 12 = 0. 2. Решите уравнение ( х + 1)( х + 3)( х + 5)( х + 7) = — 15. 3. Решите уравнение 12х²( х – 3) + 64( х – 3)² = х ⁴. 4. Решите уравнение х ⁴ — 4х³ + 5х² — 4х + 1 = 0 5. Решите систему аравнений : х ² + 2у² — х + 2у = 6, 1,5х² + 3у² — х + 5у = 12.
2 вариант 1. ( х ² — 4х)² + 7( х ² — 4х) + 12 = 0. 2. х ( х + 1)( х + 5)( х + 6) = 24. 3. х ⁴ + 18( х + 4)² = 11х²( х + 4). 4. х ⁴ — 5х³ + 6х² — 5х + 1 = 0. 5. х ² — 2ху + у² + 2х²у – 9 = 0, х – у – х²у + 3 = 0. 3 вариант . 1. ( х ² + 3х)² — 14( х ² + 3х) + 40 = 0 2. ( х – 5)(х-3)( х + 3)( х + 1) = — 35. 3. х4 + 8х²( х + 2) = 9( х+ 2)². 4. х ⁴ — 7х³ + 14х² — 7х + 1 = 0. 5. х + у + х ² + у ² = 18, ху + х ² + у² = 19.
4 вариант. ( х ² — 2х)² — 11( х ² — 2х) + 24 = о. ( х -7)(х-4)(х-2)( х + 1) = -36. Х⁴ + 3( х -6)² = 4х²(6 – х ). Х⁴ — 6х³ + 7х² — 6х + 1 = 0. Х² + 3ху + у² = — 1, 2х² — 3ху – 3у² = — 4. Дополнительное задание: Остаток от деления многочлена Р( х ) на ( х – 1) равен 4, остаток от делении на ( х + 1) равен2, а при делении на ( х – 2) равен 8. Найти остаток от деления Р( х ) на ( х ³ — 2х² — х + 2).
Ответы и указания: вариант № 1 № 2. № 3. № 4. № 5. 1. — 3; ±2; 1 1;2;3. -5; -4; 1; 2. Однородное уравнение: u = x -3, v =x² -2 ; -1; 3; 4. (2;1); (2/3;4/3). Указание: 1·(-3) + 2· 2 2. -6; -2; -4±√6. -3±2√3; — 4; — 2. 1±√11; 4; — 2. Однородное уравнение : u = x + 4, v = x² 1 ; 5;3±√13. (2;1); (0;3); ( — 3; 0). Указание: 2· 2 + 1. 3. -6; 2; 4; 12 -3; -2; 4; 12 -6; -3; -1; 2. Однородное u = x+ 2, v = x² -6 ; ±3; 2 (2;3), (3;2), (-2 + √7; -2 — √7); (-2 — √7; -2 + √7). Указание: 2 -1. 4. (3±√5)/2 2±√3 2±√3; (3±√5)/2 (5 ± √21)/2 (1;-2), (-1;2). Указание: 1·4 + 2 .
Решение дополнительного задания. По теореме Безу: Р(1) = 4, Р(-1) = 2, Р(2) = 8. Р( х ) = G(x) ( х ³ — 2х² — х + 2) + ах² + вх + с. Подставляем 1; — 1; 2. Р(1) = G(1) ·0 + а + в + с = 4, а + в+ с = 4. Р(-1) = а – в + с = 2, Р(2) = 4а² + 2в + с = 8. Решая полученную систему из трех уравнений получим: а = в = 1, с = 2. Ответ: х ² + х + 2.
Критерий № 1 — 2 балла. 1 балл – одна вычислительная ошибка. № 2,3,4 – по 3 балла. 1 балл – привели к квадратному уравнению. 2 балла – одна вычислительная ошибка. № 5. – 4 балла. 1 балл – выразили одну переменную через другую. 2 балла – получили одно из решений. 3 балла – одна вычислительная ошибка. Дополнительное задание: 4 балла. 1 балл – применили теорему Безу для всех четырех случаев. 2 балла – составили систему уравнений. 3 балла – одна вычислительная ошибка.
По теме: методические разработки, презентации и конспекты
Способы решения уравнений высших степеней. 8 класс
Данную презентацию использую при решении уравнений высших степеней в 8 классе. Решать квадратные уравнения школьники научились по формулам, а если уравнение выше второй степени? Есть ли алгоритм.
Конспект урока. Тема: «Решение уравнений высших степеней» 8 класс
Полное описание урока. Как решать уравнения выше второго порядка? Есть ли алгоритм решения? На эти и другие вопросы отвечает данный материал.
Урок-защита проектов «Решение уравнений высших степеней» 9 класс
Конспект урока по алгебре в 9 классе «Решение уравнений высших степеней», на котором учащиеся защищали свои проекты.Презентации учащихся: Решение биквадратных уравнений, Решение возвратных уравнений, .
Открытый урок по алгебре «Уравнения высших степеней»
урок по алгебре «Уравнения высших степеней».
Презентация программы элективного курса для 9-х классов «В мире уравнений высших степеней»
Это презентация поможет сформировать программу элективного курса для предпрофильной подготовки девятиклассников по теме «В мире уравнений высших степеней».
Уравнения высших степеней
Предлагаемый курс содержит недостаточно проработанные в базовом курсе школьной математики вопросы и своим содержанием сможет привлечь внимание учащихся 10 классов, которым интересна математика. .
Контрольная работа по алгебре по теме: «Многочлены. Уравнения и системы уравнений высших степеней. Теорема Безу. Повторение». 9 класс ( углубленный уровень).
В контрольной работе содержится подборка заданий углубленного уровня по теме «Многочлены. Теорема Безу. Деление с остатком. Повторение». Для сильных ребят в этой теме необходимо рассмотреть .
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
http://nsportal.ru/shkola/algebra/library/2015/06/20/uravneniya-vysshih-stepeney