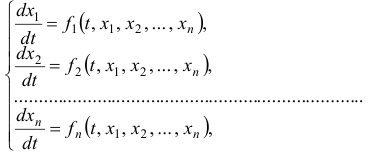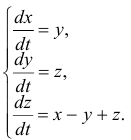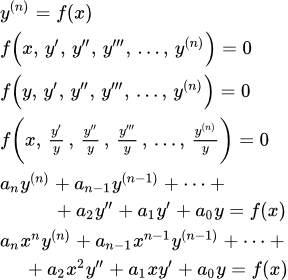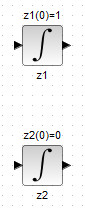Уравнения высшего порядка их сведение к системам

Сведение системы к одному дифференциальному уравнению высшего порядка

Системой дифференциальных уравнений называется совокупность уравнений, в каждое из которых входит независимая переменная, искомые функции и их производные.

Решение системы, состоящей из нескольких уравнений с таким же числом неизвестных функций, можно привести к решению дифференциального уравнения с одной неизвестной функцией.

Нормальная система уравнений:

как правило, может быть заменена одним дифференциальным уравнением, порядок которого равен порядку системы.

Пример:

Найти общее решение системы уравнений

Решение:

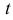
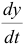
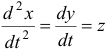
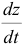
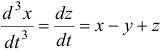
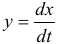
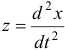
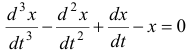
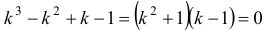
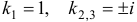
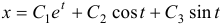
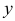
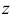
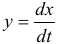
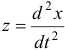
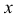
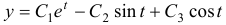
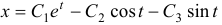
Продифференцировав первое уравнение по , заменим производную ее выражением из второго уравнения: . Продифференцировав полученное уравнение еще раз, заменим производную ее выражением из третьего уравнения: . Подставляя в последнее уравнение и , окончательно получим . Решим это уравнение. Соответствующее ему характеристическое уравнение имеет корни . Следовательно, . Функции и в соответствии с соотношениями и после дифференцирования полученного для выражения имеют вид: и .

На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Дифференциальные уравнения высших порядков

Дифференциальные уравнения высших порядков, решаемые в квадратурах

Уравнения, содержащие переменную и старшую производную

Разрешенные относительно старшей производной

Рассмотрим дифференциальное уравнение следующего вида:
.
Интегрируем n раз.
;
;
и так далее. Так же можно использовать формулу:
.
См. Дифференциальные уравнения, решающиеся непосредственным интегрированием

Разрешенные относительно переменной

Рассмотрим дифференциальное уравнение, в котором независимая переменная x является функцией от старшей производной:
.
Это уравнение можно решить параметрическим методом. Для этого вводим параметр . В результате получаем:
;
.
Из последнего уравнения . Интегрируя, получаем зависимость производной от x в параметрическом виде:
.
Продолжая интегрирование аналогичным образом, получим зависимость y от x в параметрическом виде.

Общий случай

Рассмотрим дифференциальное уравнение, содержащее только независимую переменную и старшую производную общего вида:
.
Его можно решить в квадратурах в параметрическом виде, если удастся подобрать такие функции и , для которых .

Если такие функции найдены, то положим . Тогда исходное уравнение выполняется автоматически. Дифференцируя первую функцию, находим связь между дифференциалами переменных x и t : . Тогда
.
Интегрируя последнее соотношение, получаем решение для производной более низкого порядка в параметрическом виде. Продолжая действовать подобным способом, получим общее решение в квадратурах.

Уравнения, содержащие только производные порядков n и n-1

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-1-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Тогда положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению .

Тогда
;
.
Интегрируя эти уравнения, получим параметрическое представление производной порядка n – 2 . Продолжая подобным образом, получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Уравнения, содержащие только производные порядков n и n-2

Рассмотрим дифференциальное уравнение, содержащее только производные n-го и n-2-го порядков:
.
Его можно решить в квадратурах, если удастся найти такие функции и , которые удовлетворяют уравнению
.
Положим
.
Считаем, что такое параметрическое представление эквивалентно исходному уравнению.

Тогда
;
;
;
;
.
Интегрируя, получим параметрическое представление производных порядка n, n – 1 и n – 2 . Далее интегрируем как в предыдущем случае ⇑. В результате получаем выражения остальных производных и самой функции y через параметр t .
Подробнее, см. здесь.

Дифференциальные уравнения высших порядков, допускающие понижение порядка

Уравнения, не содержащие зависимую переменную y в явном виде

Подстановка приводит к понижению порядка уравнения на единицу. Здесь – функция от .
См. Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Уравнения, не содержащие независимую переменную x в явном виде

Для решения этого уравнения, делаем подстановку
.
Считаем, что является функцией от . Тогда
.
Аналогично для остальных производных. В результате порядок уравнения понижается на единицу.
См. Дифференциальные уравнения высших порядков, не содержащие переменную в явном виде

Однородные дифференциальные уравнения высших порядков

Уравнения, однородные относительно функции и ее производных

Дифференциальное уравнение

является однородным относительно функции и ее производных, если оно обладает свойством:
.
Здесь t – число или любая функция; число p называют показателем однородности.

Чтобы распознать такое уравнение, нужно сделать замену
.
Если после преобразований t сократится, то это однородное уравнение.

Для его решения делаем подстановку
,
где – функция от . Тогда
.
Аналогично преобразуем производные и т.д. В результате порядок уравнения понижается на единицу.
См. Однородные относительно функции и ее производных дифференциальные уравнения высших порядков

Обобщенно однородные уравнения относительно переменных

Теперь рассмотрим дифференциальные уравнения, которые не меняют вида, если сделать замену переменных: , где c – постоянная; s – измерение однородности для переменной y. При такой замене производная порядка m умножается на :
.
Если записать исходное уравнение в общем виде:
,
то оно является обобщенно однородным относительно переменных, если обладает свойством:
,
где t – число или любая функция; p – показатель однородности.

При подобные уравнения можно назвать однородными дифференциальными уравнениями относительно переменных.

Порядок такого уравнения можно понизить на единицу, если искать решение в параметрическом виде, и перейти от зависимой переменной (функции) y к новой зависимой переменной (новой функции) с помощью подстановок:
, где t – параметр.
В результате для функции получим дифференциальное уравнение n — го порядка, которое не содержит переменную t в явном виде. Далее понижаем порядок изложенным выше методом ⇑.
См. Обобщенно однородные дифференциальные уравнения относительно переменных высших порядков

Дифференциальные уравнения с полной производной

Это уравнения, которые можно привести к полной производной:
.
Отсюда сразу получаем первый интеграл:
.
Он представляет собой дифференциальное уравнение, на единицу меньшего порядка по сравнению с исходным уравнением .

В качестве примера рассмотрим дифференциальное уравнение второго порядка:
.
Разделим его на . Тогда
.
Отсюда получаем первый интеграл, который является дифференциальным уравнением первого порядка:
.
См. Дифференциальные уравнения высших порядков с полной производной.

Линейные дифференциальные уравнения высших порядков

Рассмотрим линейное однородное дифференциальное уравнение n-го порядка:
(1) ,
где – функции от независимой переменной . Пусть есть n линейно независимых решений этого уравнения. Тогда общее решение уравнения (1) имеет вид:
(2) ,
где – произвольные постоянные. Сами функции образуют фундаментальную систему решений.
Фундаментальная система решений линейного однородного уравнения n-го порядка – это n линейно независимых решений этого уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка:
.
Пусть есть частное (любое) решение этого уравнения. Тогда общее решение имеет вид:
,
где – общее решение однородного уравнения (1).

Линейные дифференциальные уравнения с постоянными коэффициентами и приводящиеся к ним

Линейные однородные уравнения с постоянными коэффициентами

Это уравнения вида:
(3) .
Здесь – действительные числа. Чтобы найти общее решение этого уравнения, нам нужно найти n линейно независимых решений , которые образуют фундаментальную систему решений. Тогда общее решение определяется по формуле (2):
(2) .

Ищем решение в виде . Получаем характеристическое уравнение:
(4) .

Если это уравнение имеет различные корни , то фундаментальная система решений имеет вид:
.

Если имеется комплексный корень
,
то существует и комплексно сопряженный корень . Этим двум корням соответствуют решения и , которые включаем в фундаментальную систему вместо комплексных решений и .

Кратным корням кратности соответствуют линейно независимых решений: .

Кратным комплексным корням кратности и их комплексно сопряженным значениям соответствуют линейно независимых решений:
.

Линейные неоднородные уравнения со специальной неоднородной частью

Рассмотрим уравнение вида
,
где – многочлены степеней s 1 и s 2 ; – постоянные.

Сначала мы ищем общее решение однородного уравнения (3). Если характеристическое уравнение (4) не содержит корень , то ищем частное решение в виде:
,
где
;
;
s – наибольшее из s 1 и s 2 .

Если характеристическое уравнение (4) имеет корень кратности , то ищем частное решение в виде:
.

После этого получаем общее решение:
.

Линейные неоднородные уравнения с постоянными коэффициентами

Здесь возможны три способа решения.

1) Метод Бернулли.
Сначала находим любое, отличное от нуля, решение однородного уравнения
.
Затем делаем подстановку
,
где – функция от переменной x . Получаем дифференциальное уравнение для u , которое содержит только производные от u по x . Выполняя подстановку , получаем уравнение n – 1 — го порядка.

2) Метод линейной подстановки.
Сделаем подстановку
,
где – один из корней характеристического уравнения (4). В результате получим линейное неоднородное уравнение с постоянными коэффициентами порядка . Последовательно применяя такую подстановку, приведем исходное уравнение к уравнению первого порядка.

3) Метод вариации постоянных Лагранжа.
В этом методе мы сначала решаем однородное уравнение (3). Его решение имеет вид:
(2) .
Далее мы считаем, что постоянные являются функциями от переменной x . Тогда решение исходного уравнения имеет вид:
,
где – неизвестные функции. Подставляя в исходное уравнение и накладывая на некоторые ограничения, получаем уравнения, из которых можно найти вид функций .

Уравнение Эйлера

Оно сводится к линейному уравнению с постоянными коэффициентами подстановкой:
.
Однако, для решения уравнения Эйлера, делать такую подстановку нет необходимости. Можно сразу искать решение однородного уравнения в виде
.
В результате получим такие же правила, как и для уравнения с постоянными коэффициентами, в которых вместо переменной нужно подставить .

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 13-06-2017 Изменено: 11-05-2021

Сведение к системе дифференциального уравнения 2-ой степени в Xcos

Способ 2: сведение к системе в форме Коши

Рассмотрим более привычный и распространённый способ численного интегрирования обыкновенных дифференциальных уравнений n-го порядка: сведение к системе из n уравнений 1-го порядка, или, как ещё говорят, к нормальной форме или форме Коши.

Решение систем ОДУ без использования визульных блоков, было рассмотрено ранее в материале.

Рассмотрим дифференциальное уравнение второго порядка с заданными начальными условиями:

Введём замену переменных, сводящих уравнение (1) к системе из двух уравнений первой степени:

\begin z_1 = y \\ z_2=y’ \end

получим систему в новых фазовых переменных

(2)\begin z_1’=z_2\\ z_2′ = -2z_2+0.3z_1\\ \end (3)\begin z_1(0)=1\\ z_2(0)=0\\ \end

Данную систему нам и необходимо замоделировать. Итак, разберём, какие из функциональных бликов Xcos понадобятся, чтобы найти решение задачи Коши системы из двух дифференциальных уравнений 1-ой степени (2) с начальными условиями (3).

Система (2) содержит два д.у. первого порядка, а значит нам понадобятся два блока интегратора. Здесь и в дальнейшем для моделирования дифференциальных уравнений, вместо INTEGRAL_f, будем использовать блок с палитры «Системы с непрерывным временем». Смысловая нагрузка у блока INTEGRAL_m та же, что и у используемого ранее INTEGRAL_f, — поиск первообразной сигнала, подающегося на его вход. Однако блок INTEGRAL_m во-первых, более нагляден, а во-вторых, имеет большее количество настраиваемых внутренних параметров блока.

Итак, приступим к сбору функциональной блок-схемы, реализующей поиск численного решения системы дифференциальных уравнений (2), удовлетворяющего начальным условиям (3). Для создания блок-схемы нам потребуется:

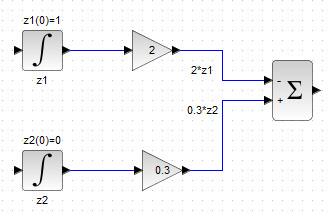
Добавить два блока INTEGRAL_m на рабочую область, дав им названия соответствующих фазовых переменных и задать во внутренних параметрах блоков INTEGRAL_m значения параметра Initial condition (начальные условия), указанные в (7б). Результатом данных действий будет схема, изображенная на рис.38;

Рисунок 38. Блоки интеграторов с заданными начальными условиями

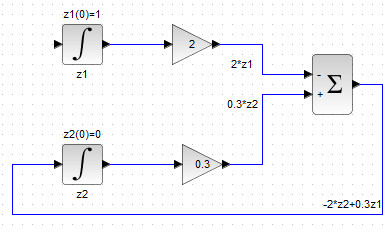
Собирать уравнения системы (2) необходимо, начиная с последнего и двигаясь вверх. Второе уравнение системы (2) имеет вид \(z_2′ = -2z_2+0.3z_1 \)и представляет собой сумму двух слагаемых с разными знаками, первое из которых увеличено в 2 раза, а второе в 0.3 раз.
Поэтому нам потребуется добавить блок сумматора BIGSOM_f, во внутренних параметрах которого указан знаков слагаемых [-1;1] и блоки усилителя GAINBLK_f со значениями 2 и 3 соответственно.
Далее необходимо составить правую част рассматриваемого уравнения, то есть подать на вход BIGSOM_f, советующие слагаемые, как показано на рис. 39.

Рисунок 39. Блок-схема правой части второго диф.уравнения системы (2)

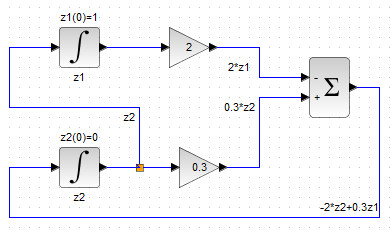
Итак, мы получили в сумматоре выражение, которые необходимо проинтегрировать, то есть подать на вход блока-интегратора INTEGRAL_m , соответствующего фазовой переменной, производная которой стоит в левой части рассматриваемого уравнения. В уравнении \(z_2′ = -2z_2+0.3z_1 \) слева стоит \(z_2′ \), а значит, выход сумматора нужно подсоединить ко входу интегратора, отвечающего за переменную \(z_2 \)(см. рис. 40).

Рисунок 40. Вывод выхода сумматора на вход интегратора

Перейдём к построению первого уравнения системы (2), имеющего вид \(z_1’=z_2 \). Фазовая переменная \(z_2 \) формируется как выход соответствующего блока интегратора. Распараллелим выход нижнего блока INTEGRAL_m , подав его на вход верхнего блока INTEGRAL_m , который соответствует фазовой переменной \(z_1 \). В результате получим схему, изображенную на рисунке 41.

Рисунок 41. Блок-схема замкнутой системы двух д.у. 1-ой степени (2)

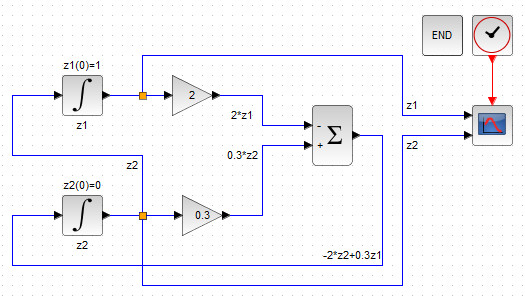
Далее нам потребуется вывести графики фазовых переменных \(z_1, z_2 \), для этого добавьте блоки CMSCOPE, END и CLOCK_c на рабочую область.

По традиции, во внутренних параметрах блока END указать время 10сек., на функциональный вход блока CMSCOPE нужно подать выход блока CLOCK_c с параметрами Period = 0.1, Время инициализации=0, а на регулярные входы осциллографа подать распараллеленные интегральные выходы, соответствующие фазовым переменным (рис. 42).

Рисунок 42. Блок-схема поиска численного задачи Коши (2-3) с выводом графиков фазовых переменных

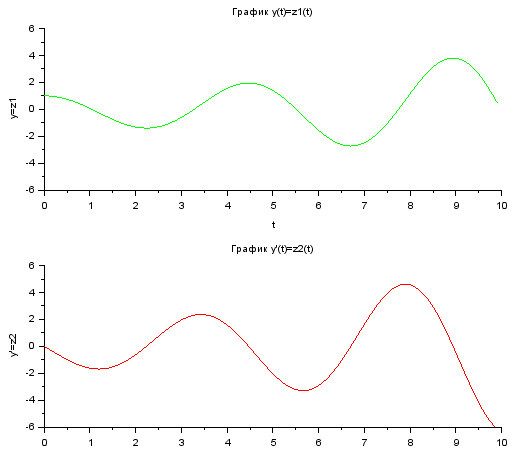
После запуска моделирования и настройки параметров осциллографа, получим графики (рис. 43).

Рисунок 43. Графическое решение задачи Коши (2-3)

Итак, основными принципами второго способа численного интегрирования дифференциальных уравнений порядка выше 1 являются:

Сведение дифференциального уравнения n-ой к системе из n уравнений 1-ой степени, путём замены переменных;

Движение снизу вверх при визуализации уравнений получившейся системы;

Параллельное включение в схему блоков INTEGRAL_m, отвечающих за фазовые переменные системы;

Отображение результата численного моделирования на системах координат фазовая переменная – время;

Задание начальных условий в соответствующих блоках-интеграторах;

Задание отрезка интегрирования во внутренних параметрах блока END, начальной точки и шага дискретизации в блоке CLOCK_c;

Возможность выбора численного метода поиска решения дифференциального уравнения в настройкам параметров интегрирования.