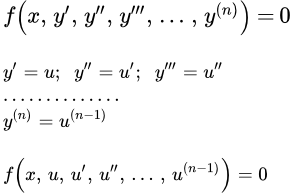Уравнения высшего порядка не содержащие функцию

Дифференциальные уравнения высших порядков, не содержащие функцию в явном виде

Метод решения

Рассмотрим уравнение, не содержащие функцию в явном виде:
(1) .
Порядок этого уравнения понижается на единицу с помощью подстановки
.

Действительно, тогда:
;
;
.
.
И мы получили уравнение, в котором порядок понижен на единицу:
.

Пример

Делаем подстановку:
.
Тогда:
.
Подставляем:
.

Разделяем переменные:
.
При u ≠ 0 имеем:
.

Интегрируем:
.
Интегрируем еще раз:
.

Окончательно имеем:
.
Заменим постоянную:
.
Тогда
.

Теперь рассмотрим случай:
.
также является решением исходного уравнения. Интегрируем:
;
.

Автор: Олег Одинцов . Опубликовано: 17-07-2013

Дифференциальные уравнения, допускающие понижение порядка

Рассмотрим три частных случая решения дифференциальных уравнений с возможностью понижения порядка. Во всех случаях понижение порядка производится с помощью замены переменной. То есть, решение дифференциального уравнения сводится к решению уравнения более низкого порядка. В основном мы рассмотрим способы понижения порядка дифференциальных уравнений второго порядка, однако их можно применять многократно и понижать порядок уравнений изначально более высокого порядка. Так, в примере 2 решается задача понижения порядка дифференциального уравнения третьего порядка.

Понижение порядка уравнения, не содержащего y и y‘

Это дифференциальное уравнение вида . Произведём замену переменной: введём новую функцию и тогда . Следовательно, и исходное уравнение превращается в уравнениие первого порядка

с искомой функцией .

Решая его, находим . Так как , то .

Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 1. Найти общее решение дифференциального уравнения

.

Решение. Произведём замену переменной, как было описано выше: введём функцию и, таким образом, понизив порядок уравнения, получим уравнение первого порядка . Интегрируя его, находим . Заменяя на и интегрируя ещё раз, находим общее решение исходного дифференциального уравнения:

Пример 2. Решить дифференциальное уравнение третьего порядка

.

Решение. Дифференциальное уравнение не содержит y и y‘ в явном виде. Для понижения порядка применяем подстановку:

.

Тогда и получаем линейное дифференциальное уравнение первого порядка:

.

Заменяя z произведением функций u и v , получим

Тогда получим выражения с функцией v :

Выражения с функцией u :

Дважды интегрируем и получаем:

.

.

Интегрируем по частям и получаем:

.

Итак, общее решение данного дифференциального уравения:

.

Понижение порядка уравнения, не содержащего y

Это дифференциальное уравнение вида . Произведём замену переменной как в предыдущем случае: введём , тогда , и уравнение преобразуется в уравнение первого порядка . Решая его, найдём . Так как , то . Отсюда, интегрируя ещё раз, получаем решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 3. Найти общее решение дифференциального уравнения

.

Решение. Уже знакомым способом произведём замену переменной: введём функцию и понизим порядок уравнения. Получаем уравнение первого порядка . Решая его, находим . Тогда и получаем решение исходного дифференциального уравнения второго порядка:

.

Пример 4. Решить дифференциальное уравнение

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Интегрируем полученную функцию:

Мы пришли к цели — общему решению данного дифференциального уравения:

.

Пример 5. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит y в явном виде. Поэтому для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это однородное уравение, которое решается при помощи подстановки . Тогда , :

Далее потребуется интегрировать по частям. Введём обозначения:

Таким образом, получили общее решение данного дифференциального уравения:

.

Понижение порядка уравнения, не содержащего x

Это уравнение вида . Вводим новую функцию , полагая . Тогда

.

Подставляя в уравнение выражения для и , понижаем порядок уравнения. Получаем уравнение первого порядка относительно z как функции от y:

.

Решая его, найдём . Так как , то . Получено дифференциальное уравнение с разделяющимися переменными, из которого находим общее решение исходного уравнения:

,

где и — произвольные константы интегрирования.

Пример 6. Найти общее решение дифференциального уравнения

.

Решение. Полагая и учитывая, что , получаем . Понизив порядок исходного уравнения, получаем уравнение первого порядка с разделяющимися переменными. Приводя его к виду и интегрируя, получаем , откуда . Учитывая, что , находим , откуда получаем решение исходного дифференциального уравнения второго порядка:

.

При сокращении на z было потеряно решение уравнения , т.е. . В данном случае оно содержится в общем решении, так как получается из него при (за исключением решения y = 0).

Пример 7. Найти общее решение дифференциального уравнения

.

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Получим дифференциальное уравнение первого порядка:

.

Это уравение с разделяющимися переменными. Решим его:

Используя вновь подстановку

,

получим ещё одно уравнение с разделяющимися переменными. Решим и его:

Таким образом, общее решение данного дифференциального уравения:

.

Пример 8. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(0) = 1 , y‘(0) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Поэтому применяем подстановку:

.

Таким образом, понизили порядок уравнения и получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделяем переменные и интегрируем:

Чтобы определить C 1 , используем данные условия y(0) = 1 , y‘(0) = −1 или p(0) = −1 . В полученное выражение подставим y = 1 , p = −1 :

.

.

Разделяя переменные и интегрируя, получаем

.

Из начального условия y(0) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Пример 9. Найти частное решение дифференциального уравнения

,

удовлетворяющее начальному условию y(1) = 1 , y‘(1) = −1 .

Решение. Дифференциальное уравнение не содержит x в явном виде. Для понижения порядка применяем подстановку:

.

Таким образом, получили уравнение первого порядка

.

Это дифференциальное уравнение с разделяющимися переменными. Разделив обе части уравнения на p , получим

Интегрируем обе части уравнения

Используем начальные условия и определим C 1 . Если x = 1 , то y = 1 и p = y‘ = −1 , поэтому

.

Из начального условия y(1) = 1 следует

.

Получаем окончательное решение данного дифференциального уравнения

.

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.

Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y

— некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y

— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y

линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.

Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

1. Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
   y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .

1. Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .

Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1

Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .

Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3

1. Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
   y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x

Общее же решение запишем так:

y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:

k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0

Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .

Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x

1. Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
   y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x

Общим решением ЛОДУ будет:

y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .

Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )

1. Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .

На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .

Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y

. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y

, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y

согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.

Когда f ( x ) представлена в виде многочлена n -ой степени f ( x ) = P n ( x ) , частным решением ЛНДУ станет: y

= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y

= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y

= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y

= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .

Коэффициенты, которые неизвестны, определяются из равенства y

( n — 1 ) + . . . + f 1 y

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.

Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .

Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .

Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:

C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x

Решаем, используя метод Крамера:

∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x

Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x

где C 4 , C 5 и C 6 – произвольные постоянные.