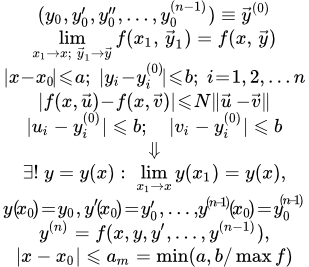Уравнения высших порядков теорема существования и единственности

Теорема существования и единственности решения дифференциального уравнения произвольного порядка

Здесь мы рассмотрим теорему существования и единственности решения дифференциального уравнения (ДУ) произвольного порядка. Для доказательства теоремы мы сведем ДУ к системе ДУ первого порядка и воспользуемся результатом теоремы существования и единственности решения системы дифференциальных уравнений.

Формулировка теоремы

Пусть дано дифференциальное уравнение n-го порядка:
(1)
с начальными условиями при :
(2) , , , . , ,
где – некоторые числа (постоянные).
Пусть – непрерывная функция от переменных в замкнутой области :
; ; ; ; . ;
и, следовательно, ограничена, по абсолютной величине, некоторым положительным значением :
(3) .
Здесь и есть некоторые положительные числа.
И пусть функция удовлетворяет в области условию Липшица:
(4) ,
где – положительное число;
; ; ; . ; ;
; ; ; . ; .
Тогда существует единственное решение уравнения (1):
,
удовлетворяющее начальным условиям (2), определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Доказательство теоремы

Приведение к системе дифференциальных уравнений

Для доказательства, приведем уравнение
(1)
к системе дифференциальных уравнений первого порядка. Для этого вводим вспомогательных функций от переменной :
.
Свяжем их соотношениями:
; ; ; . .

Дифференцируя уравнение по , находим:
;
.
Дифференцируя еще раз, имеем:
;
.
Таким образом
.
При имеем:
.
Дифференцируем по :
.

Тогда исходное уравнение (1) можно представить в виде системы дифференциальных уравнений первого порядка:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.n) ,
с начальными условиями:
(6) , , , . , .

Применение теоремы единственности и существования для системы дифференциальных уравнений

Все функции непрерывны по своим аргументам. непрерывна по условию теоремы. Остальные функции зависят только от одного из аргументов и являются линейными функциями. Поэтому они тоже непрерывны.

Все функции удовлетворяют условию Липшица. удовлетворяет условию Липшица по условию теоремы. Частные производные остальных функций либо равны нулю ( при ), либо равны единице ( при ). Поэтому частные производные непрерывны. Из этого следует, что функции удовлетворяют условию Липшица. Доказательство этого утверждения приведено в разделе “Условие Липшица”.

Итак, все условия теоремы существования и единственности решения системы ДУ выполнены. Поэтому решение системы (5) с начальными условиями (6) существует и единственно. И, следовательно, решение дифференциального уравнения (1) с начальными условиями (2) также существует и единственно.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 30-07-2016

Основные понятия и определения дифференциальных уравнений высших порядков

Дифференциальное уравнение n-го порядка имеет вид или, если оно разрешено относительно ,

Задача нахождения решения уравнения (I), удовлетворяющего начальным условиям

называется задачей Коши для уравнения (1).

Теорема существования и единственности решения задачи Коши . Если в уравнении (1) функция

а) непрерывна по всем своим аргументам в некоторой области их изменения,

б) имеет ограниченные в области частные производные по аргументам , то найдется интервал , на котором существует единственное решение уравнения (1), удовлетворяющее условиям

где значения содержатся в области .

Для уравнения второго порядка начальные условия имеют вид

где — данные числа. В этом случае теорема существования и единственности геометрически означает, что через данную точку плоскости с данным тангенсом угла наклона касательной проходит единственная кривая.

Рассмотрим, например, уравнение и начальные условия

В данном случае . Эта функция определена и непрерывна при всех значениях . Ее частные производные по и равны соответственно

и являются всюду непрерывными и ограниченными функциями своих аргументов. Следовательно, каковы бы ни были начальные условия

существует единственное решение данного уравнения, удовлетворяющее этим условиям.

Общим решением дифференциального уравнения n-го порядка (1) называется множество всех его решений, определяемое формулой , содержащей произвольных постоянных таких, что если заданы начальные условия (2), то найдутся такие значения , что будет являться решением уравнения (1), удовлетворяющим этим начальным условиям.

Любое решение, получаемое из общего решения при конкретных значениях произвольных постоянных называется частным решением дифференциального уравнения (1).

Уравнение вида , которое определяет неявно общее решение дифференциального уравнения, называется общим интегралом уравнения . Давая постоянным , конкретные допустимые числовые значения, получим частный интеграл дифференциального уравнения. График частного решения или частного интеграла называется интегральной кривой данного дифференциального уравнения.

Пример 1. Показать, что есть общее решение дифференциального уравнения .

Решение. Покажем, что удовлетворяет данному уравнению при любых значениях постоянных и . В самом деле, имеем .

Пусть теперь заданные произвольные начальные условия . Покажем, что постоянные и можно подобрать так, что будет удовлетворять этим условиям. Имеем . Полагая , получаем систему

из которой однозначно определяются и . Таким образом, решение удовлетворяет поставленным начальным условиям.

Геометрически это означает, что через каждую точку плоскости с заданным угловым коэффициентом проходит единственная прямая.

Задание одного начального условия, например , определяет пучок прямых с центром в точке , т.е. одного начального условия недостаточно для выделения единственного решения.