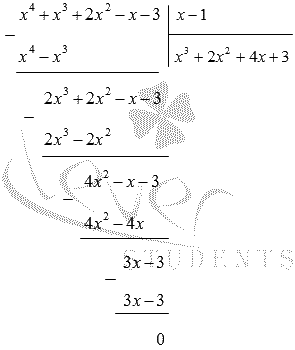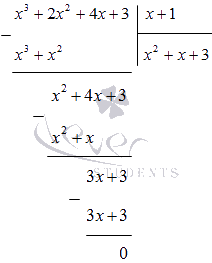«Решение уравнений высших степеней». 9-й класс
Разделы: Математика
Класс: 9
Учебная:
Развивающая:
- Развитие внимания учащихся.
- Развитие умения добиваться результатов труда.
- Развитие интереса к изучению алгебры и навыков самостоятельной работы.
Воспитывающая:
Оборудование: компьютер, проектор.
1 этап работы. Организационный момент.
2 этап работы. Мотивация и выход на постановку проблемы
Уравнение 
В школьном курсе изучения математики очень много внимания уделяется решению различного вида уравнений. До девятого класса мы умели решать только линейные и квадратные уравнения. Уравнения третьей, четвёртой и т.д. степеней называются уравнениями высших степеней. В девятом классе мы познакомились с двумя основными приёмами решения некоторых уравнений третьей и четвёртой степеней: разложение многочлена на множители и использование замены переменной.
А можно ли решить уравнения более высоких степеней? На этот вопрос мы постараемся сегодня найти ответ.
3 этап работы. Повторить ранее изученный материал. Ввести понятие уравнения высших степеней.
1) Решение линейного уравнения.
Линейным называется уравнение вида 


2) Решение квадратного уравнения.
Квадратным называется уравнение вида 







Из рассмотренных линейных и квадратных уравнений видим, что количество корней уравнения не более его степени. В курсе высшей алгебры доказывается, что уравнение 

Будем называть уравнения третьей, четвёртой и т.д. степеней уравнениями высших степеней. Некоторые уравнения высоких степеней удаётся решить с помощью двух основных приёмов: разложением многочлена 
3) Решение кубического уравнения.
Решим кубическое уравнение
Сгруппируем члены многочлена, стоящего в левой части уравнения, и разложим на множители. Получим:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три линейных уравнения:
Итак, данное кубическое уравнение имеет три корня: 


4) Решение биквадратного уравнения.
Очень распространены биквадратные уравнения, которые имеют вид 


Решим биквадратное уравнение 
Введём новую переменную 


Вернёмся к старой переменной 






Итак, данное биквадратное уравнение имеет четыре корня:



Попробуем решить уравнение 
4 этап работы. Привести некоторые утверждения о корнях многочлена вида 

Приведём некоторые утверждения о корнях многочлена вида 
1) Многочлен 


2) Многочлен нечётной степени имеет хотя бы один корень. Например, многочлены первой, третьей, пятой и т.д. степени имеют хотя бы один корень. Многочлены чётной степени корней могут и не иметь.
3) Если на концах отрезка 


4) Если число 








5) Если уравнение 



5 этап работы. Показать как применяется теория делимости для решения уравнений высших степеней. Рассмотреть примеры решения уравнений высших степеней , в которых для разложения левой части на множители используется способ деления многочлена на многочлен “уголком”.
Пример 1. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (-1), т.е. равняется одному из чисел: 




Таким образом, мы фактически разложили левую часть уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем два уравнения:
Итак, данное уравнение имеет три корня:
Пример 2. Решим уравнение 
Если это уравнение имеет целый корень, то он является делителем свободного члена (9),т.е. равняется одному из чисел: 

Значит, многочлен 



Таким образом, мы разложили левую часть уравнения на множители:
Аналогичным образом поступим и с многочленом 
Если это уравнение 


Значит, многочлен 
произведения 


Таким образом, мы разложили левую часть исходного уравнения на множители:
Произведение множителей равно нулю, если один из множителей равен нулю. Получаем три уравнения:
Итак, данное уравнение имеет четыре корня:
6 этап работы. Закрепление изученного материала.
Решите уравнения высших степеней, используя способ деления многочлена на многочлен “уголком”.
7 этап работы. Вывод урока.
Решить уравнения высших степеней можно следующим образом:
- используя формулы для нахождения корней (если они известны);
- используя замену переменной;
- раскладывая многочлен в левой части уравнения на множители, используя способ деления многочлена на многочлен “уголком”.
8 этап работы. Домашнее задание.
Дома решить уравнения высших степеней, используя способ деления многочлена на многочлен “уголком” (раздать листы с заданиями).
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Урок-защита проектов «Решение уравнений высших степеней» 9 класс
творческая работа учащихся по алгебре (9 класс) по теме
Конспект урока по алгебре в 9 классе «Решение уравнений высших степеней», на котором учащиеся защищали свои проекты.
Презентации учащихся: Решение биквадратных уравнений, Решение возвратных уравнений, Решение уравнений с помощью теоремы Безу, Графический способ решения уравнений, Нестандартные решения уравнений.
Скачать:
| Вложение | Размер |
|---|---|
| конспект урока-защиты проектов «Решение уравнений высших степеней» | 162.28 КБ |
| Решение биквадратных уравнений | 294.11 КБ |
| Решение возвратных уравнений | 390.37 КБ |
| Решение уравнений с помощью теоремы Безу | 489.71 КБ |
| Различные способы решения уранений 3 степени | 279.92 КБ |
| Нестандартные решения уравнений высших степеней | 232.61 КБ |
| Зарождение алгебры | 733.71 КБ |
Предварительный просмотр:
Урок — защита проектов по теме
«Решение уравнений высших степеней»
- сформировать представление о методах и способах решения нестандартных задач и алгебраических уравнений на уровне, превышающем уровень государственных образовательных стандартов;
- Совершенствовать навыки работы с информацией: поиск, обработка и применение.
- Развивать коммуникативные навыки учащихся: умение работать в группах, защищать свои проекты.
Эпиграф к уроку:
Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду.
Я знаю: каждый в классе гений,
Но без труда талант не впрок
Из ваших знаний и умений
Мы вместе сочиним урок.
Сегодня на уроке вы представите свои проекты по теме:»Решение уравнений высших степеней». Вы работали в группах по различным темам. Итогом вашей работы явились проекты,оформленные в виде презентаций. Чтобы материал, представленный на слайдах, был более понятен, предлагаю, некоторые способы решения уравнений воспроизводить на доске, с последующей записью в тетрадях.
Хочу напомнить, что решение некоторых рассматриваемых типов уравнений не входит в программу обычной школы.
Работая над проектами вы рассмотрели следующие группы уравнений:
А начнем нашу защиту с проекта «Зарождение алгебры», ведь недаром говорят, что алгебра – искусство решать уравнения.(см. на диске в папке «Проекты 2010г»).
Следующий проект: Решения биквадратных уравнений.
Такие уравнения мы решали на уроках алгебры. Большое спасибо ребятам за огромное количество рассмотренных уравнений. Их можно использовать как дидактический материал для других классов.
Следующая группа ребят расскажет о решении возвратных уравнений.
Попробуем решить следующее уравнение: х 4 -5х 3 +6х 2 -5х+1=0
Ребята показывают решение на доске, остальные записывают.
А следующий проект «Решение уравнений высших степеней с помощью теоремы Безу.
После просмотра презентации демонстрируется на доске решение уравнения с помощью теоремы Безу:
А одна из учениц рассмотрела решение уравнений 3 степени различными способами.
Одно уравнение можно решить несколькими способами:
Самые способные ученики вашего класса подготовили проект «Нестандартные решения уравнений высших степеней». Им пришлось очень долго и упорно собирать материал, решить все найденные уравнения.
Представьте нам одно из решений уравнения.
Спасибо, за демонстрацию своих работ.
А теперь, пока учителя, присутствующие на уроке заполняют оценочные листы, у меня к вам несколько вопросов:
• Появились ли у вас новые знания, умения в процессе работы над проектом?
• Что в работе над проектом было наиболее интересным?
• Каковы были основные трудности и как вы их преодолевали?
• Какие можете сделать себе замечания и предложения на будущее?
Давайте поблагодарим всех ребят, разработавших и представивших на наш суд свои проекты.
• Лучшему научному руководителю
• Лучшему дизайнеру и т. д.
Предварительный просмотр:
Подписи к слайдам:
Проект:»РЕШЕНИЕ УРАВНЕНИЙ ВЫСШИХ СТЕПЕНЕЙ С ПОМОЩЬЮ ЗАМЕНЫ ПЕРЕМЕННОЙ» ВЫПОЛНИЛИ УЧАЩИЕСЯ 9 кл : УТАРБАЕВА Ж., КУШКУМБАЕВ С.,БЕСПАЕВ К., ИСЕНОВ Д.
ЦЕЛИ ПРОЕКТА: 1. СОВЕРШЕНСТВОВАТЬ НАВЫКИ РЕШЕНИЯ УРАВНЕНИЯ С ПОМОЩЬЮ ЗАМЕНЫ ПЕРЕМЕННОЙ. 2. НАУЧИТЬСЯ РАБОТАТЬ С ИНФОРМАЦИЕЙ ИЗ ИНТЕРНЕТА. 3. УМЕТЬ СОЗДАВАТЬ ПРЕЗЕНТАЦИИ, ИСПОЛЬЗУЯ СОБРАННЫЙ МАТЕРИАЛ.
НЕМНОГО ИСТОРИИ… Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики
ПРАКТИЧЕСКОЕ ЗНАЧЕНИЕ РЕШЕНИЙ УРАВНЕНИЙ. . НАХОЖДЕНИЕ ПЛОЩАДИ ГЕОМЕТРИЧЕСКИХ ФИГУР. ПРИВОДИТ К РЕШЕНИЮ КВАДРАТНЫХ УРАВНЕНИЙ.
Нахождение объёма ПРИВОДИТ К РЕШЕНИЮ КУБИЧЕСКИХ УРАВНЕНИЙ.
Задачи баллистики ПРИВОДИТ К РЕШЕНИЮ КВАДРАТНЫХ, КУБИЧЕСКИХ УРАВНЕНИЙ.
Решение уравнений четвертой и пятой степени Кристаллография
Полёт самолёта Решение квадратного и кубического уравнения
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи ». Задачи часто облекались в стихотворную форму.
Уравнения, приводимые к квадратным (биквадратные) К квадратным уравнениям сводятся уравнения четвертой степени: ax 4 + bx 2 + c = 0, называемые биквадратными, причем, а ≠ 0. Достаточно положить в этом уравнении х 2 = y , следовательно, ay ² + by + c = 0 найдём корни полученного квадратного уравнения y 1,2 = заменим y на x и получим
x ⁴ — 25x² + 144 = 0 x ⁴ — 25x² + 144 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 25y + 144 = 0 D = 25² — 4 • 1 • 144 = 625 — 576 = 49 y ₁ = 16 y ₂ = 9 значит, x ² = 16; x ² = 9 Ответ: x ₁ = 4; x ₂ = -4; x ₃ = 3; x ₄ = -3
x ⁴ — 4x² + 4 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 4y + 4 = 0 D = 4² — 4 • 1 • 4 = 16 — 16 = 0 значит, y = 2 Ответ: x ₁,₂ = ±√
x ⁴ — 2x² — 3 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 2y — 3 = 0 D = 2² — 4 • 1 • (-3) = 4 — (-12) = 16 y ₁ = 3 y₂= -1 значит, x ² = 3; x ² = -1 Ответ: x ₁,₂=±√3;
9x⁴ — 9x² + 2 = 0 сделаем замену x ² = y получим квадратное уравнение 9y² — 9y + 2 = 0 D = 9² — 4 • 9 • 2 = 81 — 72 = 9 значит, y ₁ =2/3; y₂=1/3 x ² = 2/3 ; x ² = 1/3 Ответ: x ₁,₂=±√6/3 x ₃,₄=±√3/3
4 x ⁴ — 5 x ² + 1 = 0 сделаем замену x ² = y получим квадратное уравнение 4 y ² — 5 y + 1 = 0 D = 5² — 4 • 4 • 1 = 25 — 16 = 9 y₁ = 1 y₂ = 0,25 значит, x² = 1; x² = 0,25 Ответ: x₁ = 1; x₂ = -1; x₃ = 0,5; x₄ = -0,5
5x⁴ — 5x² + 2 = 0 сделаем замену x ² = y получим квадратное уравнение 5y² — 5y + 2 = 0 D = 5² — 4 • 5 • 2 = 25 — 40 = -15 Ответ: нет корней
x ⁴ + 5x² — 36 = 0 сделаем замену x ² = y получим квадратное уравнение y ² + 5y — 36 = 0 D = 5² — 4 • 1 • (-36) = 25 — (-144) = 169 y ₁ = 4 y ₂ =-9 значит, x ² = 4; x ² = -9 Ответ: x ₁ = 2; x ₂ = -2
x ⁴ — 6x² + 8 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 6y + 8 = 0 D = 6² — 4 • 1 • 8 = 36 — 32 = 4 y ₁ = 4 y ₂ =2 значит, x ² = 4; x ² = 2 Ответ: x ₁ = 2; x ₂ = -2 ; x₃ = √ 2 ; x₄ = — √ 2
x ⁴ + 10x² + 25 = 0 сделаем замену x ² = y получим квадратное уравнение y ² + 10y + 25 = 0 D = 10² — 4 • 1 • 25 = 100 — 100 = 0 y = -10 ± 0 / 2 • 1 = -10 / 2 = -5 Ответ: нет корней
x ⁴ + x ² — 2 = 0 сделаем замену x ² = y получим квадратное уравнение y ² + y — 2 = 0 D = 1² — 4 • 1 • (-2) = 1 — (-8) = 9 y ₁ = 1 y ₂ = -2 значит, x ² = 1; x ² = -2 Ответ: x ₁ = 1; x ₂ = -1
x ⁴ — 8x² — 9 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 8y — 9 = 0 D = 8² — 4 • 1 • (-9) = 64 — (-36) = 100 y ₁ = 9 y ₂ =-1 значит, x ² = 9; x ² = -1 Ответ: x ₁ = 3; x ₂ = -3
x ⁴ — 7x² — 144 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 7y — 144 = 0 D = 7² — 4 • 1 • (-144) = 49 — (-576) = 625 y ₁ = 16 y ₂ =-9 значит, x ² = 16; x ² = -9 Ответ: x ₁ = 4; x ₂ = -4
36x⁴ — 3x² + 1 = 0 сделаем замену x ² = y получим квадратное уравнение 36y² — 3y + 1 = 0 D = 3² — 4 • 36 • 1 = 9 — 144 = -135 Ответ: нет корней, так как дискрим и нант отрицательный!
16x⁴ + 10x² + 1 = 0 сделаем замену x ² = y получим квадратное уравнение 16y² + 10y + 1 = 0 D = 10² — 4 • 16 • 1 = 100 — 64 = 36 y ₁ = -0,125 y ₂ = -0,5 значит, x ² = -0,125; x ² = -0,5 Ответ: нет корней
x ⁴ — 8x² + 16 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 8y + 16 = 0 D = 8² — 4 • 1 • 16 = 64 — 64 = 0 y = 8 / 2 = 4 Ответ: x = 2; х ₂= -2
x ⁴ — 25x² = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 25y = 0 y ₁ = 25 y ₂ = 0 значит, x ² = 25; x ² = 0 Ответ: x ₁ = 0; x ₂ = 5; x ₃ = -5
x ⁴ + 15x² + 50 = 0 сделаем замену x ² = y получим квадратное уравнение y ² + 15y + 50 = 0 D = 15² — 4 • 1 • 50 = 225 — 200 = 25 y ₁ = -5 y ₂ = -10 значит, x ² = -5; x ² = -10 Ответ: нет корней
x ⁴ — 5x² — 36 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 5y — 36 = 0 D = 5² — 4 • 1 • (-36) = 25 — (-144) = 169 y ₁ =9 y ₂ = -4 Значит, x ² = 9; x ² = -4 Ответ: x ₁ = 3; x ₂ = -3
x ⁴ + 10x² + 25 = 0 сделаем замену x ² = y получим квадратное уравнение y ² + 10y + 25 = 0 D = 10² — 4 • 1 • 25 = 100 — 100 = 0 y = -5 Ответ: нет корней
x ⁴ — 6x² + 8 = 0 сделаем замену x ² = y получим квадратное уравнение y ² — 6y + 8 = 0 D = 6² — 4 • 1 • 8 = 36 — 32 = 4 y ₁ = 4 y ₂ = 2 Значит, x ² = 4; x ² = 2 Ответ: x ₁ = 2; x ₂ = -2; x ₃ = √2; x ₄ =-√2
5x⁴ — 5x² = 0 сделаем замену x ² = y получим квадратное уравнение 5y² — 5y = 0 y ₁ = 1 y ₂ = 0 Значит, x ² = 1; x ² = 0 Ответ: x ₁ = 0; x ₂ = 1; x ₃ = -1
x ⁴ + 6x² = 0 сделаем замену x ² = y получим квадратное уравнение y ² + 6y = 0 y ₁ = 0 y ₂ = -6 Значит, x ² = 0; x ² = -6 Ответ: x = 0
(5 X +1)² +6(5 X +1)-7 =0 Замена: 5 X +1= y. Получим уравнение: y²+6y-7=0 D =36+28=64 y₁=1 ; y₂= -7 ; 5X+1=1 5X+1= -7 5X=0 5 X =-8 X=0 ; X = -1,6
( X² -9) ² -8( X² -9)+7=0 Замена: X² -9= y. Получим уравнение: y ²-8y+7=0 D =64-28=36 y₁=7 ; y₂=1 X² -9= 7 или X² -9=1 X=±4 x=±√10
(2х 2 +3х) 2 -7(2х 2 +3х)=-10
12 февраля 1535 года между Фиори и Н.Тартальей состоялся научный поединок, на котором Тарталья одержал блестящую победу. Он за два часа решил все предложенные Фиори 30 задач, в то время как сам Фиори не решил ни одной задачи Тартальи. В нашей презентации всего 25 уравнений. Попробуйте решить их за урок. Н. Тарталья
Предварительный просмотр:
Подписи к слайдам:
Решение возвратных уравнений Проект по алгебре. Выполнили: Дубровская Настя, Тимофеева Алина,Смирнова Маша.
Цели проекта: Познакомиться с методами решения возвратных уравнений. Совершенствовать навыки решения уравнений. Овладеть способами сбора и хранения информации (создать презентацию)
Возвратные уравнения Возвратное уравнение – алгебраическое уравнение а 0 х n + a 1 x n – 1 + … + a n – 1 x + a n =0, в котором а к = a n – k , где k = 0, 1, 2 … n , причем, а ≠ 0. Задачу нахождения корней возвратного уравнения сводят к задаче нахождения решений алгебраического уравнения меньшей степени. Термин возвратные уравнения был введён Л. Эйлером.
Уравнения, у которых коэффициенты членов, равноудаленных от «начала» и «конца» уравнения, равны между собой, называются симметричными . 6х 4 -35х 3 +62х 2 -35х+6=0 Симметричные уравнения четвертой степени. 1)Если m = 1, то это симметричное уравнение первого рода, имеющее вид ax 4 + bx 3 + cx 2 + bx + a = 0 и решающееся новой подстановкой y = 2) Если m = -1, то это симметричное уравнение второго рода, имеющее вид ax 4 + bx 3 + cx 2 — bx + a = 0 и решающееся новой подстановкой y =
Алгоритм решения уравнений
х 4 – 5х 3 + 8х 2 – 5х + 1 = 0
Х 4 +х 3 -4х 2 +х +1=0
х 4 -5х 3 +6х 2 -5х+1=0
3х 4 + 5х 3 – 14х 2 -10х + 12=0
5х 3 + 21х 2 +21х + 5=0 симметрическое уравнение
6х 4 -3х 3 + 12х 2 – 6х = 0
Предварительный просмотр:
Подписи к слайдам:
ПРОЕКТ ПО АЛГЕБРЕ Решение уравнений высших степеней с помощью теоремы Безу. Выполнила ученица 9 класса Зингейской СОШ Батраканова Махабат.
Цели ПРОЕКТА: 1. овладеть способом решения уравнений высших степеней с помощью теоремы Безу. 2. использовать ресурсы интернета. 3. создать презентацию, используя собранный материал
Только в 11 веке таджикский поэт и ученый Омар Хаям впервые решил уравнение III степени. Установить, существует ли формула для нахождения корней любого уравнения, пытались многие. Но в конце 18 века французский ученый Луи Лагранж пытался доказать невозможность алгоритма общих уравнений, а вначале 19 века француз Галуа развил идею Лагранжа. С тех пор математика пошла другим путем. Ученые стали искать другие методы решения уравнений высших степеней . Одним из них является метод разложения многочлена на множители с использованием теоремы Безу.
Этьен Безу Французский ученый-математик, член Парижской Академии наук. Годы жизни: 1733-1783гг. Изучал системы алгебраических уравнений высших степеней;
Этьен Безу Установил общие методы решения уравнений высших степеней; Знаменитость ему принесла теорема. Алгебраические работы Безу опубликованы в мемуарах Академии
х 4 +4х 3 -18х 2 -12х+9=0 Р(-1)=1-4-18+12+9=-22+22=0. Вывод: «-1»– корень уравнения. Найдем делители свободного члена и выясним, при каком из них левая часть равна нулю. Делители:-1;1;-3;3;-9;9. Р(-1)= Р(1)= Р(-3)= Р(3)= и т.д.
х 4 +4х 3 -18х 2 -12х+9=0
х 4 +4х 3 -18х 2 -12х+9=0 Значит, данное уравнение можно разложить на следующие множители
как решают эти уравнения: х 4 -2х 3 -7х 2 +4х+4=0 Делители 4 :1; -1; 2; -2; 4; -4 Р (1) = 1-2-7+4+4=0 (х-1)(х 3 -х 2 -8х-4)=0 Делители 4 :1; -1; 2; -2; 4; -4 Р(-2)= -8-4+16-4=0 (х-1)(х+2)(х 2 -3х-2)=0 х-1=0 или х+2=0 или х 2 -3х-2=0 х₁=1 х₂=-2 D=9+8=17 х₃= х ₄= Ответ: х ₁= 1; х ₂= -2; х ₃= ; х₄=
Ответ: х ₁=4, х₂,₃=1± Делители 8: 1; -1 ; 2 ; -2; 4; -4; 8; -8; Р (4)=64-96+24+8=0 (х-4)(х 2 -2х-2)=0 х-4=0 или х 2 -2х-2=0 х ₁=4 Д=4+8=12 х₂,₃= 1± х 3 -6х 2 +6х+8=0
х 3 -8х 2 +13х-2=0 Делители 2 : -1; 1; -2; 2 Р (2)=8-32+26-2=0 (х-2)(х 2 -6х+1)=0 х-2=0 или х 2 -6х+1=о х ₁ =2 D=36-4=32 х ₂,₃= 3 ± 2 √2 Ответы: х ₁=2, х₂,₃=3±2√2
х 3 -4х 2 +3х+2=0 Делители 2 : -1; 1; -2; 2 Р(2)=8-16+6+2=0 (х-2)(х 2 -2х-1)= 0 Х – 2=0 или х ² — 2х – 1=0 Х ₁ =2 D=4+4=8 х ₂.₃= 1±√2 Ответ : х₁=2, х₂.₃= 1±√2
х 3 +2х 2 +3х+2=0 Делители 2 : -1; 1; -2; 2 Р (-1)=-1+2-3+2=0 (х+1)(х 2 +х+2)=0 х+1=0 или х 2 +х+2=0 х ₁= — 1 Д= — 7 корней нет Ответ: х ₁= -1.
х 3 +4х 2 +х-6=0 Делители 6 : 1; -1; 2; -2; 3; -3; 6; -6 Р(1)=1+4+1-6=0 (х-1)(х 2 +5х+6)=0 Х-1=0 или х 2 +5х+6=0 Х ₁ =1 D=25-24=1 х ₂= — 2, х₃= — 3 Ответ : -3, -2 ; 1.
х 3 +6х 2 -х-6=0 Делители 6: 1; -1; 2; -2; 3; -3; 6; -6 Р (1)=1+6-1-6=0 (х-1)(х 2 +7х+6)=0 х-1=0 или х 2 +7х+6=0 х ₁ =1 D=49-24=25 х ₂ =-6 х ₃ =-1 Ответ:-6; -1; 1.
х 3 +4х 2 -9х-36=0 Делители 36 : 1; -1; 2; -2; 3; -4; 6; -6; 9; -9; 12; -12; 18; -18; 36; -36 Р(-3)=27-36-27+36=0 х+3=0 или х 2 +х-12=0 х ₁ =-3 D=1+48=49 х ₂=3 х₃= -4 (х+3)(х 2 +х-12)=0 Ответ: -4;-3; 3.
Предварительный просмотр:
Подписи к слайдам:
Выполнила ученица 9 класса Зингейской СОШ Пушкарева Марина Проект по алгебре: «Решение уравнений третьей степени различными способами».
Цель проекта: Совершенствовать свои умения и навыки при решении уравнений; Познакомиться с историческими сведениями о решении уравнений; Представить материал в виде презентации.
Омар Хайям ( ок . 1048- ок . 1123) Описал всевозможные виды уравнений третьей степени и рассмотрел сложные и красивые способы геометрических построений для отыскания их решения.
В начале XVI века в крупных торговых городах Северной Италии были популярны математические состязания. Математики публично вызывали соперников на поединок, причем на победителя обычно делались денежные ставки. В это время быстро распространялось преподавание арифметики, необходимой в торговле, и публичные состязания обеспечивали соперничающим преподавателям известность и привлекали учеников. Задачи формулировались для числовых значений, но иногда требовали решения алгебраических уравнений более высокого порядка. Результаты состязаний обнародовались, но методы решения математических задач — оружие в борьбе за репутацию и доходы — каждый из участников противоборства предпочитал держать в секрете.
Николо Тарталья (ребёнок из очень бедной семьи, мать не могла платить за образование, поэтому мальчик в школе узнал только половину азбуки, всеми остальными знаниями он овладел самостоятельно). В 6 лет он получил удар мечом в гортань от французского воина и с тех пор говорил с трудом, отсюда и прозвище Тарталья (заика). Он вывел формулы для решения уравнений 3-ей степени, но своё открытие держал в тайне. Никколо Тарталья (1499-1557)
Джероламо Кардано (медик) занимался астрологией, составлял гороскопы. Кардано неоднократно обращался к Тарталье с просьбой сообщить ему формулу для решения кубических уравнений и обещал хранить её в секрете. Он не сдержал слово и опубликовал формулу, указав, что Тарталье принадлежит честь открытия «такого прекрасного и удивительного, превосходящего все таланты человеческого духа». Джероламо Кардано (1501-1576)
x³-3x-2 =0 1) Разложение на множители: x³-3x-2=x³+x²-x²-x-2x-2=0 x²(x+1)-x(x+1)-2(x+1)=0 (x+1)(x²-x-2)=0 x=-1 D=1+8=9 x₁=2 x₂=-1 Ответ: -1; 2.
2) Решение с помощью теоремы Безу: x³-3x-2=0 x³-3x-2=0 (-1)³ -3(-1)-2=0 x=-1 x³-3x-2 x+1 x³+x² x²-x-2 -x²-3x -x²-x -2x-2 -2x-2 0 x³-3x-2 =(x+1)(x²-x-2)=0 Ответ: -1; 2.
3) Графический способ решения: x³-3x-2=0 Ответ: -1; 2.
x³-7x+6=0 1) Разложение на множители: x³-7x+6=0 x(x²-1)-6(x-1)=0 x(x-1)(x+1)-6(x-1)=0 (x²+x-6)(x-1)=0 D=1+24=25 x-1=0 x₁=2 x=1 x₂=3 Ответ: -3; 1; 2.
2) Решение с помощью теоремы Безу: 1³-7+6=0 1³-7+6=0 x³-7x+6 x-1 x³-x² x²+x-6 x²-7x -x²+x -6x+6 -6x+6 0 x³-7x+6=(x-1)(x²+x-6) x=1 x²+x-6=0 D=1+24=25 x₁=2 x₂=-3 Ответ: -3; 1; 2.
3) Графический способ решения: Ответ: -3; 1; 2.
x³-13x+12=0 1) Разложение на множители: x³-13x+12=0 x³-x-12x+12=0 x(x²-1)-12(x-1)=0 x(x-1)(x+1)-12(x-1)=0 (x²+x-12)(x-1)=0 D=1+48=49 x=1 x₁=3 x₂=-4 Ответ: -4 ; 1; 3.
2) Решение с помощью теоремы Безу: x³-13x+12=0 x³-13x+12=0 1-13+12=0 x=1 x³-13x+12 x-1 x³-x² x²+x-12 x²-13x x²-x -12x+12 -12x+12 0 x³-13x+12=(x-1)(x²+x-12)=0 x=1 D=1+48=49 x₁=3 x₂=-4 Ответ: -4; 1; 3.
3) Графический способ решения: Ответ: -4; 1; 3.
2x³+x²-3=0 1) Разложение на множители: 2x³+x²-3=0 3x³-x³+x²-3=0 3(x³-1)-x²(x-1)=0 3(x-1)(x²+x+1)-x²(x-1)=0 (x-1)(3x²+3x+3-x²)=0 (x-1)(2x²+3x+3)=0 x=1 2x²+3x+3=0 D=9-24=-15 Ответ: 1.
2) Решение с помощью теоремы Безу: 2x³+x²-3=0 2x³+x²-3 x-1 2x³-2x² 2x²+3x+3 3x²-3 3x²-3x 3x-3 3x-3 0 (x-1)(2x²+3x+3)=0 x=1 или 2x²+3x+3=0 D=9-24=-15 Ответ: 1.
3) Графический способ решения: Ответ: 1.
Предварительный просмотр:
Подписи к слайдам:
Проект: Нестандартные решения уравнений высших степеней. Выполнил: Бекбаев Адильжан Абаевич и Туржанов Руслан Муратович Учитель: Горбунова Татьяна Ивановна.
Цели проекта: 1. Совершенствовать навыки решения уравнении высших степеней нестандартными способами. 2. Оформить решение уравнений на слайдах в презентации .
(x+1)(x+2)(x+4)(x+5)=40 (x 2 +6x+5)(x 2 +6x+8)=40 Сделаем замену: x 2 +6x=t (t+5)(t+8)=40 t 2 +13t=0 t(t+13)=0 t 1 =0 t 2 = — 13 Получим уравнения: x 2 +6x=0 x(x+6)=0 x =0 x =-6 Ответ: x 1 =0 ; х 2 =- 6 x 2 +6 x =-13 x 2 +6 x +13=0 Д=36-52=-16 нет решений
x(x+1)(x+2)(x+3)=24 Ответ: x 1 =1; х 2 =-4
(x+1)(x+2)(x+3)(x+4)=360 (x 2 +5x+4)(x 2 +5x+6)=360 x 2 +5x=t (t+4)(t+6)=360 t 2 +10t+24=360 t 2 +10t+336=0 Д =100+1344=1444 Ответ: x 1 =2; х 2 = -7
(x-1)(x-3)(x-5)(x-7)=105 (x 2 -8x+7)(x 2 -8x+15)=105 x 2 -8x=t (t+7)(t+15)=105 t 2 +22t+105=105 t 2 +22t=0 t(t+22)=0 t=0 t=-22 x 2 -8 x =0 x ( x -8)=0 x =0 x =8 Ответ: x 1 =0; х 2 =8 x 2 -8 x =-22 x 2 -8 x +22=0 Д=64-88=-24 нет решений
(x-1)(x-2)(x-3)(x-4)=840 Ответ: х 1 =8; х 2 =-3
(x+1)(x+3)(x+5)(x+7)=945 Ответ: х 1 =2; х 2 =-10
( x +1)( x +2)( x +4)( x +3)=15
( x -4)( x 2 +15 x +50)( x -2)=18 x 2 Ответ: х 1 =-4; х 2 =5; х 3,4 =-5 ± 3
( x 2 +3 x +3)( x 2 -2 x +3)=24 x 2
Предварительный просмотр:
Подписи к слайдам:
Зарождение алгебры Выполнили: Бикмурзина Сабина , Тажибаева Жанара
Цели проекта: Познакомиться с информацией о решении уравнений в процессе формирования науки алгебры . Совершенствовать навыки работы с образовательными ресурсами в Интернете. Уметь оформлять полученные результаты в виде презентации.
Алгебра-часть математики, которая изучает общие свойства действий над величинами и решение уравнений, связанных с этими действиями. Слово «алгебра» возникло после появления трактата « Китаб аль-ждебр валь-мукабала » хорезмского математика и астронома Мухаммеда Бен Мусса аль-Хорезми (787-850г.г.) В этом труде он описал краткое сочинение о вычислениях посредством « аль-ждебр валь-мукабала », понимая под этим метод решения уравнений. Метод этот сводился к двум операциям : перенос членов из одной части в другую ( аль-ждебр ) и приведение подобных членов ( валь-мукабала ).
Диофант жил в четвертом веке до нашей эры. ученый отошел от традиционных в греческой математике геометрических проблем и занялся алгеброй. Основное его произведение «Арифметика». Сохранилось 6 томов из предполагаемых 13; в них содержится 189 уравнений с решениями. Автор интересуется только одним решением: положительным и рациональным. Диофант не применял общих методов решения уравнений: методы у него меняются от одного уравнения к другому. При выборе коэффициентов уравнений, чтобы получить желаемое рациональное и положительное решение, Диофант применяет много остроумных приемов.
«Путник! Здесь прах погребен Диофанта. И числа поведать могут, о чудо, сколь долог был век его жизни. Часть шестую его представляло детство. Двенадцатая часть протекла еще жизни – покрылся пухом тогда подбородок. Седьмую в бездетном браке провел Диофант. Прошло пятилетие; он был осчастливлен рожденьем прекрасного первенца сына, коему рок половину лишь жизни прекрасной и светлой дал на земле по сравненью с отцом. И в печали глубокой старец земного удела конец воспринял, переживши года четыре с тех пор, как сына лишился. Скажи, сколько лет жизни достигнув, смерть воспринял Диофант?»
Решение: X лет — продолжительность жизни Диофанта Надпись на могиле приводит нас к уравнению первой степени, решив которое, находим, что Диофант прожил 84 года.
Мухаммед ибн Муса ал-Хорезми – крупнейший ученый первой половины IX века, труды которого сыграли огромную роль в развитии математики и естествознания вначале в обширном регионе азиатской культуре, а затем начиная с XII века, и в Европе. Сейчас установлено, что ал-Хорезми был автором следующих сочинений: 1) «Книга об индийской арифметике» 2) «Краткая книга об исчислении алгебры и алмукабалы »; 3) «Астрономические таблицы ( зидж )»; 4) «Книга картины Земли »; 5) «Книга о построении астролябии»; 6) «Книга о действиях с помощью астролябии»; 7) «Книга о солнечных часах »; 8) «Трактат об определении эры евреев и их праздниках»; 9) «Книга истории». Предполагают, что он родился в городе Хиве, о его жизни почти ничего не известно. Научной работой аль-Хорезми в основном занимался в Багдаде. Его труды в течение нескольких веков оказывали сильное влияние на ученых Востока и Запада.
Учебник математики Ал-Хорезми , выпущенный им около 830 года под заглавием „ Китаб мухтасар аль-джебр ва ал- мукабала » , посвящен в основном решению уравнений первой и второй степени. Этот математик уравнения решает также геометрически. Вот пример, ставший знаменитым, из «Алгебры» ал — Хорезми: х 2 +10х = 39 . В оригинале эта задача формулируется следующим образом: « Квадрат и десять корней равны 39».
Китаб — книга мухтасар – краткая аль — артикль джебр — восстановление ва – союз «и» ал-мукабала — противопоставление
При решении уравнения Если в части одной, Безразлично какой, Встретится член отрицательный, Мы к обеим частям, С этим членом сличив, Равный член придадим, Только с знаком другим, — И найдем результат нам желательный Ал-джабра
Ал-мукабала Дальше смотрим в уравнение, Можно ль сделать приведенье, Если члены в нем подобны, Сопоставить их удобно, Вычтя равный член из них, К одному приводим их.
6х -13 2х -5 = 13 -2х 4х = 8 2 = х Ал-джабра Ал-мукабала Решить уравнение: 6х-13=2х-5
Узбекский математик, поэт и врач Омар Хайям уже в IX веке систематически изучил уравнения третьей степени, дал их классификацию, выяснил условия их разрешимости (в смысле существования положительных корней). Хайям в своём алгебраическом трактате говорит, что он много занимался поисками точного решения уравнений третьей степени В 8 лет знал Коран по памяти, глубоко занимался математикой, астрономией, философией. В 12 лет Омар стал учеником Нишапурского медресе . Он блестяще закончил курс по мусульманскому праву и медицине, получив квалификацию хакима , то есть врача. Но медицинская практика мало интересовала Омара. Он изучал сочинения известного математика и астронома Сабита ибн Курры , труды греческих математиков.
Однажды во время чтения «Книги об исцелении» Абу Али ибн Сины Хайям почувствовал приближение смерти (а было тогда ему уже за восемьдесят). Остановился он в чтении на разделе, посвященном труднейшему метафизическому вопросу и озаглавленному «Единое во множественном», заложил между листов золотую зубочистку, которую держал в руке, и закрыл фолиант. Затем он позвал своих близких и учеников, составил завещание и после этого уже не принимал ни пищи, ни питья. Исполнив молитву на сон грядущий, он положил земной поклон и, стоя на коленях, произнёс: «Боже! По мере своих сил я старался познать Тебя. Прости меня! Поскольку я познал Тебя, постольку я к Тебе приблизился». С этими словами на устах Хайям и умер.
Джероламо Кардано ( 1501 — 1576 ) – врач, философ, математик и механик – в своей книге, посвященной алгебре, указал «формулу Кардано » — формулу для нахождения корня уравнения третьей степени: С 1534 года Кардано начал чтение лекций по математике и медицине в Миланском университете. . Работы Кардано сыграли большую роль в развитии алгебры; одним из первых в Европе он стал допускать отрицательные корни уравнений. С именем Кардано связывают формулу решения неполного кубического уравнения. Одиннадцать лет спустя он издал свой значительный труд по математике, озаглавленный „ Artis magnae sive de regulis algebraicis liber unus «. Именно этот труд обусловил выдающееся место Кардано в истории развития математики .
Согласно легенде, Кардано предсказал день своей смерти и, чтобы оправдать своё предсказание, покончил с собой. С юности Джероламо обуревала жажда славы. На склоне лет он писал в своей автобиографии: Цель, к которой я стремился, заключалась в увековечении моего имени, поскольку я мог этого достигнуть, а вовсе не в богатстве или праздности, не в почестях, не в высоких должностях, не во власти. Учился в университетах Павии и Падуи . Занимался сначала исключительно медициной, но в 1534 стал профессором математики в Милане , позже — в Болонье , хотя доходное врачебное занятие не бросил и завоевал репутацию одного из лучших европейских врачей. Подрабатывал также составлением астрологических альманахов и гороскопов . За составление и публикацию гороскопа Иисуса Христа был обвинён в ереси ( 1570 ), провёл несколько месяцев в тюрьме и был вынужден уехать в Рим просить у Папы отпущение грехов. Женился в 1531 году . Старший сын Кардано был осуждён за убийство изменницы-жены и казнён ( 1560 ), из-за чего Кардано и переехал в Болонью . Младший сын стал игроком и воровал деньги у отца.
Никколо Тарталья (1499-1557) – учитель математики — заново открыл метод Даль Ферро. Итальянский математик Тарталья Труды посвящены вопросам математики, механики, баллистики, геодезии, фортификации и др. В сочинении «Новая наука» (1537г.) он показал, что траектория полёта снаряда на всём протяжении есть кривая линия (парабола) и что наибольшая дальность полёта снаряда соответствует углу в 45°. Другая его важная работа — «Общий трактат о числе и мере» (части 1-6, 1556-60г.), который содержит обширный материал по вопросам арифметики, алгебры и геометрии. Имя Тарталья, наряду с именем Дж. Кардано , связано с разработкой способа решения кубических уравнений .
12 февраля 1535 года между Фиори и Н.Тартальей состоялся научный поединок, на котором Тарталья одержал блестящую победу. Он за два часа решил все предложенные Фиори 30 задач, в то время как сам Фиори не решил ни одной задачи Тартальи.
Вначале Декарт готовился к военной карьере, но увлекся математикой, которая привлекла его достоверностью своих выводов. Но и ему не было условий для научной работы. Иезуиты выступают против учения Декарта, угрожают ему расправой и заставляют покинуть Францию. Двадцать лет он живет в Голландии, последние два года жизни он провел в Швеции, создавая Академию наук. Климат Швеции подорвал здоровье ученого, и он умирает вдали от родины от воспаления легких. Декарт внес большой вклад в геометрию, алгебру. С его именем связаны такие понятия, как координаты, произведение, парабола, овал и другие. Декарт всю жизнь опасался неодобрения со стороны могущественного ордена иезуитов. Декарт был мишенью для яростных нападок церковников. Впоследствии произведения Декарта были присуждены к сожжению как еретически
Франсуа Виет (1540-1603) – «отец алгебры» — открыл несколько способов решения уравнений четвертой и пятой степени. Франсуа Виет по образованию юрист. Он много занимался адвокатской деятельностью, а с 1571 по 1584 г. Был советником королей Генриха III , а после его смерти – Генриха IX
Благодаря трудам Виета открылась возможность выражения свойств уравнений и их корней общими формулами. Виет нашел общие методы решений уравнений второй, третьей и четвертой степени, унифицировал методы, найденные раннее Ферро и Феррари, а также вывел общеизвестные теперь формулы суммы и произведения корней квадратного уравнения (формулы Виета). Впервые свои исследования по математике Виет опубликовал в книге «Математический канон» в 1574 году. Эта книга печаталась за счет Виета и поэтому вышла очень небольшим тиражом. Его работы были написаны столь трудным для понимания математическим языком, что не нашли такого распространения, которого заслуживали. Все свои математические труды Виет опубликовал в 1591 году в книге „ Isagoge in artem analiti — cam «. Они свидетельствовали о всесторонности его знаний. Спустя 40 лет после смерти Виета его произведения были изданы под общим заглавием “Opera mathematica ”.
Голландский ученый Андриан Ромен вызвал на поединок всех математиков мира, предложив им решить уравнение 45 степени. Коэффициенты были очень большими числами, один из них был равен 488494125. 53-летний Виет указал 23 корня уравнения, остальные 22 корня были отрицательные, а Виет отрицательных чисел на признавал. Как к Виету пришла слава
Теорема, выражающая связь между коэффициентам и квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. «Если В + D , умноженное на А минус А 2 , равно BD , то А равно В и равно D ».
Другие научные заслуги Виета: знаменитые « формулы Виета » для коэффициентов многочлена как функций его корней ; новый тригонометрический метод решения неприводимого кубического уравнения , применимый также для трисекции угла; первый пример бесконечного произведения: полное аналитическое изложение теории уравнений первых четырёх степеней; идея применения трансцендентных функций к решению алгебраических уравнений; оригинальный метод приближённого решения алгебраических уравнений с числовыми коэффициентами; частичное решение задачи Аполлония о построении круга, касающегося трёх данных, в сочинении Apollonius Gallus (1600). Решение Виета не проходит для случая внешних касаний. [2]
« Алгебраические обозначения получают усовершенствование у Виета и Декарта ; начиная с Декарта алгебраическая запись мало чем отличается от современной » . Андронов А.А., советский математик
«Люди, незнакомые с алгеброй, не могут представить себе тех удивительных вещей, которых можно достигнуть … при помощи названной науки.» Г.В. Лейбниц
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
http://nsportal.ru/shkola/algebra/library/2012/12/02/urok-zashchita-proektov-reshenie-uravneniy-vysshikh-stepeney-9