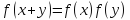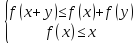Урок по теме функциональные уравнения

Обучение старшеклассников решению функциональных уравнений. Композиция функций
статья по алгебре (9 класс) на тему

Первый урок по изучению темы «Функциональные уравнения». Направлен на формирование знаний о функциональных уравнениях, композиции функции и о методах построения композиции функций.

Скачать:

Предварительный просмотр:

Конспект урока по теме: «Композиция функций»

Тип: урок ознакомления с новым материалом;

Тема: «Композиция функций».

Цели: формирование знаний о композиции функций; развитие умений распознавать сложную функцию, представлять сложные функции в виде композиций элементарных функций, составлять сложную функцию из набора элементарных; воспитание добросовестного отношения к учебе, самостоятельности при работе с учебной литературой.

Оборудование: опорный конспект по теме: «Композиция функций», набор матрешек, плакат с изображением схемы композиции функций, мел, доска.

1. Постановка темы и целей урока (3 мин.);

2. Подготовка к изучению нового материала (5 мин.);

3. Ознакомление с новым материалом (20 мин);

4. Первичное осмысление и применение изученного материала (10 мин);

5. Подведение итогов урока (4 мин.);

6. Постановка домашнего задания (3 мин.);

Основное содержание учебного материала

1. Постановка темы и целей урока

После проверки готовности класса к уроку сообщает, что на данном уроке будет рассмотрена тема «Композиция функций». Ставится задача: научиться распознавать сложную функцию, представлять ее в виде композиции элементарных, составлять ее из набора элементарных, находить ее область определения. Говорит, что композиция функций встречается повсеместно, но, самое главное, что с ней можно столкнуться в заданиях ЕГЭ.

Записывать тему урока

2. Подготовка к изучению нового материала

Задание: Найдите значение функции при

Просит обучающихся вспомнить какие функции относятся к элементарным.

Предлагает устно выполнить задание.

Поясняет, что выполнение этих заданий поможет для осознанного усвоения нового материала.

Обучающиеся говорят, что к элементарным относятся: линейная , квадратичная , обратная пропорциональность ( ), степенная , все тригонометрические и обратные им.

3. Ознакомление с новым материалом

Определение: Пусть функция определена на множестве и – область ее значений. Пусть далее, функция определена на множестве . Поставим в соответствие каждому из число . Тем самым на множестве будет задана функция . Ее называют композицией функций или сложной функцией.

Предлагает рассмотреть расположение двух матрешек, вложенных одна в другую. Таким образом, одна матрешки – имеет простую структуру, две матрешки, когда, одна находится внутри другой, имеет более сложную структуру и т. д. Чем больше матрешек внутри, тем сложнее получается и структура. То же самое можно сказать и о функции.

Давайте рассмотрим следующую функцию:

Мы, вспомнили основные элементарные функции и их свойства, какие из них мы можем увидеть в составе данной формулы? (вопрос для Никифорова В.)

Учитель соглашается с ответом Никифорова и говорит, что одна функция как бы «вложена» в другую: в , в , т.е. образовалась композиция.

Предлагает записать определение композиции функций.

То есть, осмыслив определение, сделать вывод, что мы повсеместно встречаемся с композицией функций (сложной функцией). Но, можно составлять композицию не только из двух функций, но и более.

Предлагает рассмотреть 2 функции:

Просит Рожкову Н. назвать отличия и сходства данных функций.

Просит Матушкина А. ответить на вопрос: Как найти значение этой функции в фиксированной точке х ? (фиксирует на доске)

Делает вывод: Иными словами, сначала нужно найти значение функции g(х)=х-2 , а потом найти значение функции f= , которая сама по себе является функцией. В подобных случаях говорят, что задана сложная функция f (g(х)).

В нашем примере (записывает на доске) f(u)= где и= g(х)=х-

-2. Переменную и называют внутренней переменной или промежуточной (соответственно, внутренней или промежуточной функцией), а f(и) называют внешней функцией . Таким образом:

Слушают объяснения учителя, внимательно смотрят на модели

Функциональные уравнения.

знакомство с нестандартными приёмами решения уравнений, которые базируются на различных свойствах функций: чётности или нечётности, монотонности, периодичности и т.п.

Просмотр содержимого документа
«Функциональные уравнения.»

МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»

Учебное пособие для дополнительных занятий в математических кружках

ученик 10 К класса МАОУ «Лицея №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина»

Козадаев В.С., кандидат педагогических наук, учитель математики

Книга адресована для школьников, руководителей математических кружков и всех любителей математики.

Пособие состоит из трёх частей:

Функциональные уравнения: классификация и методы решения;

Применение функциональных уравнений в решении задач;

Дополнение (Историческая справка+задачник).

© МАОУ «Лицей №14 имени Заслуженного учителя Российской Федерации А.М. Кузьмина», 2016

В последнее время ключевую роль при успешном поступлении в ведущие вузы страны играет хорошее выступление на различных олимпиадах школьников (Всероссийская олимпиада школьников; олимпиады, проводимые вузами: «Физтех», «Росатом», «Ломоносов», «Покори Воробьёвы горы» и многие другие), а также сдача вступительных экзаменов в эти вузы (в основном, такие испытания проводит МГУ). Одна из тем, которая встречается в предлагаемых задачах, — функциональные уравнения. Таким образом, это пособие поможет абитуриентам при подготовке к поступлению в технические вузы. (Так, например, в 2016 году функциональные уравнения встречались в заочных турах олимпиад САММАТ и университета ИТМО по математике)

Также функциональные уравнения находят свое применение и в решении задач, напрямую с ними не связанными, причем не только в математике, но и других образовательных областях, например, в физике.

Глава I. Функциональные уравнения: классификация и методы решения. §1. Основные понятия и классификация функциональных уравнений

Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений). Решить функциональное уравнение – значит найти все функции, которые тождественно ему удовлетворяют.

Примеры функциональных уравнений:

1)

2)

3)

Наиболее важны и известны уравнения Коши:

В современной математике изучаются, в основном, дифференциальные уравнения, т.к. они имеют большое прикладное применение в физике и технике. Однако они практически не встречаются в олимпиадных задачах, потому что их решение зачастую требует специфических знаний из высшей математики, поэтому в нашем пособии мы их рассматривать не будем.

Несмотря на то, что каждая олимпиадная задача с функциональными уравнениями имеет своеобразный подход к решению, всё же можно выделить некоторые группы уравнений, объединенных общей идеей решения, основанной на каком-то математическом методе (метод подстановок) или анализе свойств функции (чётность/нечётность, монотонность, непрерывность и др.).

Итак, выделим следующие группы функциональных уравнений по методу их решения:

Метод подстановок (метод сведения к системе уравнений).

Использование функциональных уравнений с известными решениями.

В таких вузовских олимпиадах, как САММАТ, ИТМО встречались уравнения на 1-3 методы. Они проще и требуют скорее объёмных преобразований, чем специальных знаний и творческого подхода, в то время как 4 метод этом смысле сильно разнится с ними (задачи на него были на Всеросе, ММО, Турнире городов).

§2. Перебор переменных

Метод перебора переменных – самый простой среди выделенных мною.

Суть метода: подставить несколько каких-то «краеугольных» значений (0, 1, 2, -1 и т.д.) вместо переменных в данное функциональное уравнение, получив таким образом систему уравнений, и решить её.

1)Найти все такие функции, которые удовлетворяют системе неравенств

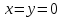
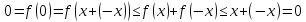
Возьмем . Тогда:

⇒

⇒

Ответ: .

2) Найти все такие функции, которые удовлетворяют равенству

Ответ: .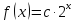

§3. Метод подстановок

Метод подстановок довольно схож с методом перебора переменных.

Суть метода: подставить вместо переменных какие-то выражения вида g(x) так, чтобы получить решаемую систему уравнений.

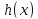
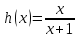
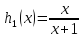
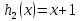
Не всегда очевидно, какое именно выражение g(x) нужно подставить вместо x в аргументах функции вида (в первом примере , во втором , ). В таких случаях имеет смысл решить уравнение h(g(x))=x (или какому-то другому , все зависит от конкретного примера). В результате получаем решаемую систему уравнений.

1) Найти все такие функции, которые удовлетворяют равенству

Подставляем в уравнение вместо x найденную g(x):

2) Найти все такие функции, которые удовлетворяют равенству

Если действовать точно так же, как и в первом примере, быстро и красиво не получится. Но тем не менее, если вместо подставить , а уже потом применять метод подстановок, то получим систему уравнений:

Несмотря на внешнюю сложность, по сути система эквивалентна:

, откуда легко находим , т.е.

Метод подстановок бывает довольно громоздким и сложным в вычислениях и преобразованиях, но применяется часто.

§4. Использование функциональных уравнений с известными решениями

Суть метода: применить при решении функциональные уравнения, для которых уже известны описываемые решения.

1) Найти все такие функции, которые удовлетворяют равенству

Возьмем вспомогательную функцию

Подставим в исходное уравнение

Т.е. функция g(x) удовлетворяет уравнению Коши, откуда

2) Найти все такие функции, которые удовлетворяют равенству

Поделим исходное уравнение на .

Введем дополнительную функцию

Т.е. функция удовлетворяет третьему уравнению Коши, откуда

Важно заметить, что метод Коши применяется для непрерывных функций.

Суть метода: постепенное отыскание решения функционального уравнения (вначале на множестве натуральных чисел, затем, с помощью математической индукции, на множестве целых, рациональных и, в заключение, действительных чисел).

Аддитивное уравнение Коши:

Решение (в непрерывных функциях).

Функция , где – решение этого уравнения, однако просто «заметить» недостаточно, необходимо строгое доказательство.

Докажем, что за знак функции можно выносить рациональные числа, т.е.

Воспользуемся индукцией. Для натуральных чисел имеем: . База очевидна. Докажем переход от к . . . Теперь докажем . . Последние два равенства и означают . Тогда имеем:

. Теперь воспользуемся леммой*: если функции совпадают во всех рациональных точках, то они равны. Тогда имеем:

Лемма. Если значения двух непрерывных функций совпадают во всех рациональных точках, тогда во всех действительных точках.

Пусть – иррациональная точка. Выберем последовательность рациональных точек , сходящуюся к (например, последовательность десятичных приближений по недостатку).

Тогда в силу непрерывности функции последовательность будет сходиться к .

Аналогично, последовательность будет сходиться к .

По условию Переходя в этом равенстве к пределу при , получим .

Поскольку выбиралась произвольно, лемма доказана.

Самому решить это уравнение довольно сложно, если не невозможно, так что такой метод нужно просто запомнить.

Глава II.Применение функциональных уравнений в решении задач.

В пособии применение функциональных уравнений в решении задач будет рассмотрено, в первую очередь, с точки зрения идеи создания выделенной в классификации. Иными словами, методы решения таких задач основаны на свойствах функций, а не на методах решения функциональных уравнений (однако, если задача по сути представляет собой функциональное уравнение, конечно, применять метод подстановок и т.п. можно и нужно).

Конечно, легко решить это уравнение с помощью равносильного перехода или замены переменной. Однако есть и другой, не менее простой, метод решения.

Рассмотрим функцию с областью определения . , значит 0 – корень уравнения. – сумма двух непрерывных возрастающих функций и , следовательно, найденный корень – единственный.

(МГУ, БиоФак, 2005)

Запишем неравенство в виде , где . Область определения функции . – сумма двух непрерывных монотонно убывающих функций , т.е. убывающая.

Заметим, что , тогда неравенство равносильно системе:

(МГУ, ХимФак, 1989)

Данное уравнение имеет вид:

Функция определена на всей числовой прямой и является нечетной. При функция монотонно возрастает, будучи произведением двух монотонно возрастающих функций, принимающих только положительные значения( и ). Ввиду своей нечетности функция возрастает и при .

Пусть для двух чисел и выполняется равенство , т.е. . Поскольку , , что ввиду монотонности функции равносильно или . Таким образом, задача равносильна уравнению , т.е. .

Парабола симметрична относительно прямой , поэтому значения этой функции в точках и могут совпадать в двух случаях: точки и совпадают или они симметричны относительно .

Таким образом, имеем 2 случая:

Откуда легко находим (см. задачу 1) корни.

Глава III. Дополнение Историческая справка

Краткая история развития теории функциональных уравнений.

Проблема решения функциональных уравнений появилась одновременно с зарождением теории функций. В 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения. Н. И. Лобачевский получил формулу угла параллельности из функционального уравнения. Также английский математик Ч. Бэббидж рассматривал некоторые геометрические задачи с точки зрения функциональных уравнений. Г. Дарбу применял их к проблеме параллелограмма сил и к основной теореме проективной геометрии.

В современной математике рассматриваются, в основном, дифференциальные уравнения, которые находят широкое применение в физике и технике.

Краткая биография Коши.

Огюсте́н Луи́ Коши́ (21 августа 1789— 23 мая 1857) — блестящий французский математик и механик, член Парижской академии наук, Лондонского королевского общества, Петербургской академии наук и других академий.

Основные направления научной деятельности:

Математический анализ. О. Л. Коши впервые дал строгое определение основным понятиям математического анализа — пределу, непрерывности, производной, дифференциалу, интегралу, сходимости ряда и т. д. Курсы анализа Коши, основанные на систематическом использовании понятия предела, послужили образцом для большинства курсов позднейшего времени..

Алгебра (доказал основную теорему теории симметрических многочленов, развил теорию определителей, найдя все главные их свойства, в частности теорему умножения (причем Коши исходил из понятия знакопеременной функции)).

Физика и механика. Внёс значительный вклад в формирование математического аппарата механики сплошных сред. Он первым стал рассматривать условия равновесия и движения выделенного объёма сплошной среды, на который действуют объёмные и поверхностные силы. В 1827 г. Коши установил свойство взаимности напряжений: давления на двух пересекающихся площадках с общим центром и одинаковой площадью обладают тем свойством, что проекция одного из них на нормаль ко второй площадке равна проекции второго давления на нормаль к первой площадке.

О. Л. Коши внес огромный вклад в развитие теории функциональных уравнений. Так, например, широко распространены уравнения Коши:

В области теории дифференциальных уравнений Коши принадлежат: постановка одной из важнейших общих задач теории дифференциальных уравнений (задача Коши), основные теоремы существования решений для случая действительных и комплексных переменных (для последних он развил метод мажорант) и метод интегрирования уравнений с частными производными 1-го порядка (метод Коши — метод характеристических полос).

Применение функциональных уравнений в физике.

Многочисленные задачи, связанные с описанием физических явлений и процессов, приводят к дифференциальным уравнениям в частных производных. Среди таких уравнений наиболее простыми и в то же время наиболее важными являются так называемые линейные дифференциальные уравнения первого и второго порядков в частных производных.

Рассмотрим уравнение , где – неизвестная функция двух переменных и ; и – заданные гладкие функции от , . Оно допускает следующее геометрическое толкование. Пусть в каждой точке области на плоскости задан вектор с координатами , . Тогда производная искомой функции в направлении векторного поля равна нулю. В частности, линии уровня функции в каждой точке касаются векторов . Таким образом, геометрически уравнение задает векторное поле, векторы которого касаются линий уровня искомой функции .

Решение уравнения сводится к решению системы обыкновенных дифференциальных уравнений.

Такой вид имеет, например, уравнений колебаний струны: , где – функция, описывающая колебания струны.

Также функциональными в физике являются уравнение теплопроводности, уравнение Лапласа и другие. Однако решение этих уравнений уходит в область математического анализа, и описанные в пособии методы там никак не применимы.

Урок по теме «Функциональные уравнения и нестандартные методы их решения»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Конспект урока по теме: «Уравнения вида и нестандартные методы их решения»

Тип: урок – конференция.

Тема: «Уравнения вида и нестандартные методы решения ».

формирование знаний об уравнениях вида и нестандартных методах их решения ;

развитие способности анализировать нестандартные ситуации, навыков работы с информационными технологиями, умения выступать на публике;

воспитание добросовестного отношения к учебе, самостоятельности при работе с учебной литературой.

Оборудование: опорный конспект по теме: «Уравнения вида и нестандартные методы решения », мультимедийная аппаратура, мел, доска.

Предварительная подготовка: за неделю до урока 4 обучающихся получают задание: изучить теоретический материал и подготовить презентацию по конкретному методу решения уравнений. За всеми необходимыми консультациями они могут обращаться к учителю.

1. Постановка темы и целей урока (3 мин.);

2. Выступление учителя (5 мин.);

3. Выступление обучающихся (31 мин);

4. Подведение итогов урока (3 мин.);

5. Постановка домашнего задания (3 мин.);

После проверки готовности класса к уроку сообщает, что на данном уроке будет рассмотрена тема «Уравнения вида

и нестандартные методы решения ».

Ставится задача: рассмотреть уравнения вида и нестандартные методы их решения. Говорит, что уравнения такого вида встречаются довольно часто, но, самое главное, что с ними можно столкнуться в олимпиадных заданиях и заданиях ЕГЭ.

Записывают тему урока

2. Выступление учителя

В последние годы издано достаточно много пособий, справочников, посвященных задачам, которые для школьников считаются задачами повышенной трудности, требующими нестандартных методов решения. Во многих из таких сборников приводятся методы решения уравнений и неравенств, основанные на свойствах функций (монотонности, ограниченности, четности, периодичности), приложениях производной. Однако примеры, приводимые в указанных пособиях и справочниках, сами обычно имеют нетрадиционный вид. Это создает дополнительные психологические трудности при усвоении данных примеров. В то же время имеется класс уравнений, который позволяет естественным образом превратить эти приемы из нестандартных в традиционные. Сегодня речь пойдет о примерах, которые можно и нужно решать не известными методами, а с использованием свойств функций, в них входящих. Все записи вам необходимо оформить в виде таблицы, которая будет заполняться в ходе выступления ваших одноклассников. Таблица имеет вид ( приложение ) :