Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок № 49. Системы тригонометрических уравнений.
Перечень вопросов, рассматриваемых в теме:
- что такое система тригонометрических уравнений;
- как решать системы тригонометрических уравнений;
- какие приемы можно использовать при решении систем тригонометрических уравнений.
Глоссарий по теме
Система уравнений – это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных.
Записывается с помощью знака <

Решением системы уравнений называется упорядоченный набор чисел (значений переменных), при подстановке которых вместо переменных каждое из уравнений обращается в верное равенство.
Колягин Ю.М., под ред. Жижченко А.Б. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – М.: Просвещение, 2010. — 368 с.
Амелькин,, В.В., Рабцевич В.Л., Задачи с параметрами: Справ. пособие по математике – М.: «Асар», 1996. – 752 с.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Основными методами решения систем уравнений являются:
— метод замены переменной.
Также при решении систем тригонометрических уравнений используются многие тригонометрические формулы.
Рассмотрим решение систем тригонометрических уравнений.
При решении этой системы можно действовать по-разному:
1) можно использовать формулы преобразования произведения в сумму синусов (в первом уравнении) или косинусов (во втором уравнении)
2) можно использовать формулами косинуса суммы и разности во втором уравнении.
Воспользуемся формулой преобразования произведения косинусов в сумму косинусов:

Теперь, учитывая, что косинус двойного аргумента может быть выражен через квадрат синуса и косинуса аргумента, возведем в квадрат первое уравнение. Но, так как возведение в квадрат не является равносильным преобразованием, введем ограничение:




Теперь введем новые переменные:



Решим ее методом подстановки.





С учетом условия 


Ответ:
Или
Рассмотрим еще один пример.
С учетом области определения уравнений 

Теперь сложим эти уравнение, оставив в системе, например, первое уравнение:



Теперь выразим из второго уравнения y:







Ответ: 
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Решите систему уравнений:
Введем новые переменные: 
Тогда вспомогательная система будет иметь вид:




Получаем четыре пары решений для вспомогательной системы:




Так как 


Решите систему уравнений: 
Пусть 
Система примет вид: 
Ее можно решить методом подстановки или методом алгебраического сложения:





Ответ:
Урок системы тригонометрических систем уравнений
Тема . Решение систем тригонометрических уравнений
Цель урока: познакомить учащихся с отдельными приемами решения систем тригонометрических уравнений.
И. Проверка домашнего задания
1. Четыре ученики воспроизводят решения домашних заданий: упражнение№ 2 (10; 18; 26; 38).
2. Устное решения тригонометрических уравнений, используя таблицу «Тригонометрические уравнения».
Таблица 11
sin x =
cos x =
tg x =
с tg x =
sin x = —
с os x = —
2 sin x cos x = 1
cos2 x — sin2 x = 1
cos2 x =
sin x — cos x = 0
sin x + cos x = 0
sin2 x + cos2 x = 0
sin2 x + cos2 x = 1
II. Повторение сведений о методах решения систем алгебраических уравнений
1. Решите систему уравнений (методом добавления).
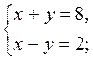
2. Решите систему уравнений.
III . Восприятия и осознания материала о решение систем тригонометрических уравнений
Основные методы решения систем тригонометрических уравнений почти такие, как и методы решения алгебраических систем.
Пример 1. Решить систему уравнений:
Прибавив и вычтя (1) и (2) уравнение, получаем
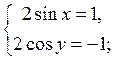
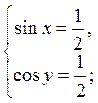
Ответ: х = (-1) 

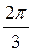

Пример 2. Решите систему уравнений:
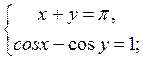
Решение
Из первого уравнения находим у = n — х. Тогда cos х — cos ( n — х) = 1, cos х + cos х = 1, 2 cos х = 1, cos х = 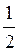


Затем находим: y= π — 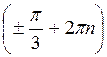


Ответ: х = ± 


Пример 3. Решите систему уравнений:
Решение
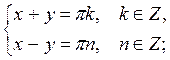
Ответ: х = 


IV. Формирование умений решать системы тригонометрических уравнений
Решить систему уравнений:
а) 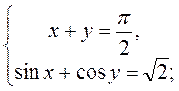
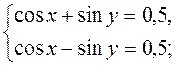
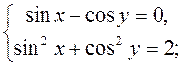
Ответы: а) x 1 = 

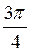


б) х = ± 


в) х = 



г) х = — 



V. Подведение итогов урока
VI. Домашнее задание
Решить системы уравнений:
а) 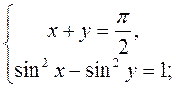
Ответ: а) х= 

б) х= (-1) k 


Е.П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического
анализа
10 класс
учреждений. Базовый и
§ 21. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Работу выполнила: Мусина В.А. студентка группы 45.3
Системы тригонометрических уравнений решаются с помощью тех же методов, что и алгебраические системы, в частности это исключение неизвестных и замена переменных. Исключить неизвестные можно с помощью одного из двух приемов:из одного уравнения выразить какое-то неизвестное (или функцию от него) и подставить его в другие или преобразовать данные уравнения и потом составить из них комбинации, в которых число неизвестных уменьшается.
Задача 1 . Решите систему уравнений


Получаем
Замечание. Если бы для нахождения значения y мы не рассмотрели отдельно формулу (1) со знаком «+» и знаком «–», то вместе с верными решениями получили бы и посторонние решения заданной системы.
Действительно, в таком случае имеем
Тогда, например, при n = 0 получаем
Таким образом, кроме решений, которые вошли в ответ, мы имеем еще две возможности:
Но эти пары значений х и у не являются решениями заданной системы, поскольку они не удовлетворяют первому уравнению.
Поэтому следует запомнить:
Когда решение уравнения cos x = а приходится применять для дальнейших преобразований, то удобно записывать его в виде двух формул: отдельно со знаком «+» и отдельно со знаком «–».
Задача 2 . Решите систему уравнений

Представим последнюю систему в виде совокупности двух систем, записывая решения второго уравнения отдельно со знаком «+» и отдельно со знаком «–»:
Почленно складывая и вычитая уравнения этих систем, находим x и y:
Замечание. В запись ответа вошли два параметра n и k, которые независимо друг от друга «пробегают» множество целых чисел. Если попробовать при решении заданной системы воспользоваться только одним параметром, например n, то это приведет к потере решений. Таким образом, в каждом случае, когда система тригонометрических уравнений приводится к системе, состоящей из элементарных тригонометрических уравнений (то есть из уравнений вида sin x = a, cos x = a, tg x = a, ctg x = a), при решении каждого из этих уравнений необходимо использовать свой целочисленный параметр.
Вопросы для контроля
- Какие методы используются для решения систем тригонометрических уравнений?
- Объясните, в каком случае при формальном решении системы уравнений
мы можем потерять часть решений, а в каком случае —получить посторонние решения. Решите эту систему.
Упражнения
Решите систему уравнений (1–8).
http://na-uroke.in.ua/27-138.html
http://ya-znau.ru/znaniya/zn/282











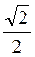
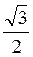
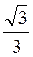
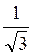
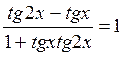
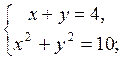
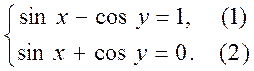
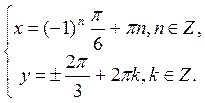
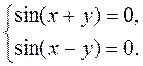
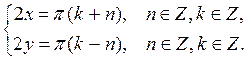
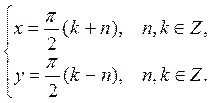
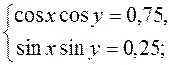
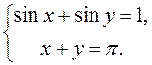



.png)
.png)





 мы можем потерять часть решений, а в каком случае —получить посторонние решения. Решите эту систему.
мы можем потерять часть решений, а в каком случае —получить посторонние решения. Решите эту систему.