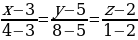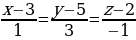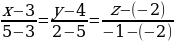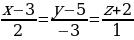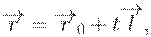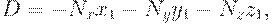Урок уравнение сферы плоскости и прямой

Составление уравнений сферы, плоскости, прямой.
план-конспект занятия по геометрии (10, 11 класс)

Составление уравнений сферы, плоскости, прямой.

Скачать:

Предварительный просмотр:

Составление уравнений сферы, плоскости, прямой.

Цели: формировать умение обучающихся решать задачи на данную тему; развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, воспитание трудолюбия, усердия в достижении цели, формировать общие компетенции ОК.2, ОК.3, ОК.4, ОК.5, ОК.6.

Справочный материал и примеры.

Теоретический материал для самостоятельного изучения:

Общее уравнение прямой имеет вид: Ax + By + C , где А, В, С – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: ( n 1; n 2 ) Координаты точки ( х 0 ; у 0 ) .

Уравнение прямой по точке и направляющему вектору: Если известна некоторая точка, принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле: n 1 (x-х 0 )+n 2 (y-у 0 )=0

Общее уравнение плоскости:

Общее уравнение плоскости имеет вид Ax +By+Cz+D=0 , где коэффициенты A, B, C, D одновременно не равны нулю.

Уравнение плоскости по точке и направляющему вектору: Если известна некоторая точка, принадлежащая плоскости, и вектор n, перпендикулярный этой плоскости (который называют вектором нормали к плоскости), то уравнение данной плоскости можно составить по формуле:

A(x-х 0 )+B(y-у 0 )+C(z-z 0 )=0

Уравнение поверхности сферы:

Сфера радиуса R с центром в начале координат представлена уравнением второй степени. x 2 +y 2 +z 2 =R 2 (R – радиус сферы)

Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.

(x−a) 2 +(y−b) 2 +(z−c) 2 =R 2 (R — радиус сферы; a, b, c — смещение центра сферы относительно центра координат)

Задания для практической работы:

1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.
2. Найти центр и радиус сферы (х+ 4) 2 + (y —3) 2 + z 2 =100.
3. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.
4. Составить уравнение прямой по точке и направляющему вектору М (4, -2), n (3,2)
5. Составить уравнение плоскости по точке Р (4, -2; -1) и вектору нормали, n (-5;3,-2)
6. Доказать, что уравнение х 2 + у 2 + z 2 —2х+ 4у—6z+ 5 = 0, является уравнением сферы.
7. Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).
8. Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору ВС, если А(-4; 2; -1), В(1; 2;-1), С(-2; 0; 1).

1. Какой вид имеет общее уравнение плоскости?
2. Какой вид имеет уравнение плоскости по точке и вектору нормали?
3. Какой вид имеет уравнение прямой по точке и направляющему вектору?
4. Какой вид имеет общее уравнение прямой?
5. Какой вид имеет уравнение сферы?

Уравнение прямой, плоскости и сферы

306 гр. Математика. Дистанционное обучение. Тема 1-3.

Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»

Тема 1: Уравнение прямой в пространстве.

З адание: записать конспект и выполнить самостоятельную работу.

Пример 1. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ: 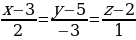Самостоятельная работа

Пример 1. Составить уравнение прямой, проходящей через две точки:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Пример 3. Составить уравнение прямой, проходящей через две точки:

Тема 2: Уравнение плоскости в пространстве

Задание: записать конспект и выполнить самостоятельную работу

П 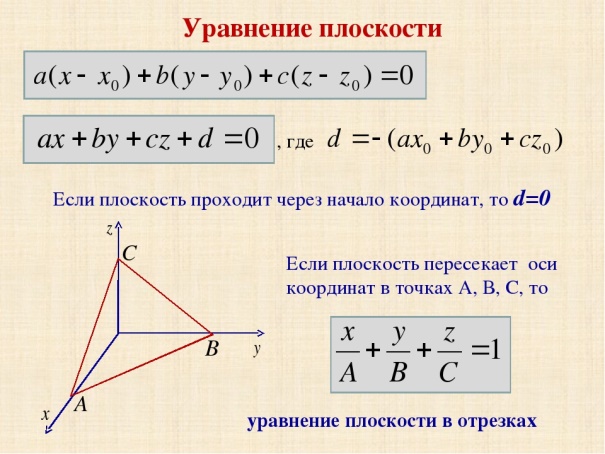ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.

Ответ: точка В (-1; 2; 7) принадлежит плоскости.

Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0

0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно

Ответ: точка Е(0; 4; -6) не принадлежит плоскости.

Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

Решение: Подставим координаты точки в уравнение и найдем D.

Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением

Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением

Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0

Решить задания №1, №2

О пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.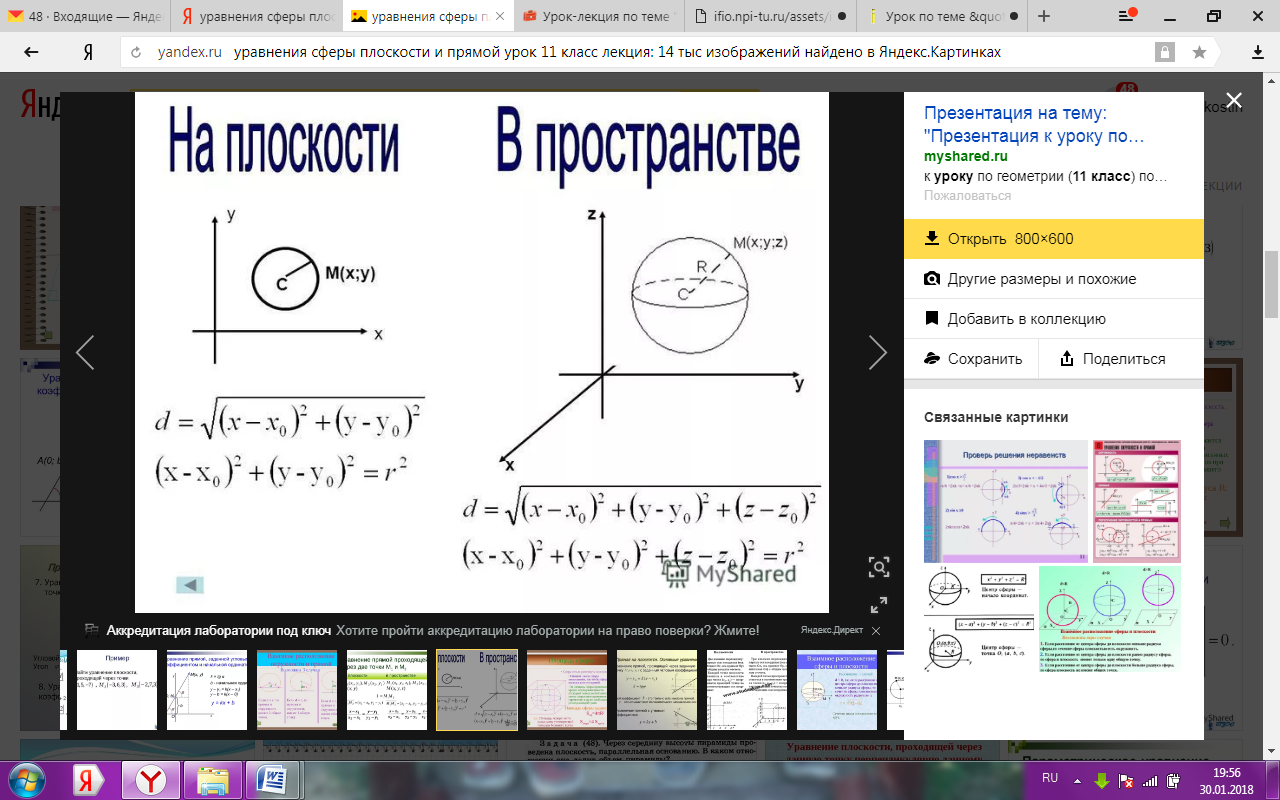

R – радиус сферы, т. О – центр сферы.

Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.

Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .

Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.

1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64

2)найдем радиус: R 2 =64, R=√64=8,

Ответ: О(6, -3, 4), R = 8.

Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6

Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.

Уравнения прямой и плоскости

Практическое занятие 36

Форма проведения: Практическая

Обучающая: закрепить понятие уравнения сферы,плоскостии прямой

Развивающая: развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию; интерес к предмету; творческие способности учащихся.

Воспитывающая: воспитывать взаимопомощь у учащихся через работу в группах; уважение к мнению других.

раздаточный материал: карточки с заданиями, заготовки для вывода уравнения сферы, шкалы для оценки урока на этапе рефлексия, маркеры, магниты, чистые листы;

глобус, разминка для глаз в виде полушарий земной поверхности;

Ход урока

Девиз урока Математику нельзя изучать, наблюдая, как это делает сосед! Древнегреческий поэт Нивен

Уравнения прямой и плоскости

Уравнение прямой на плоскости в декартовой системе координат можно задать уравнением вида

для случая, когда прямая не параллельна оси OY, и уравнением

для вертикальной прямой. Но прямая может быть также задана и другим способом. Достаточно указать вектор направления этой прямой и какую-нибудь точку , лежащую на этой прямой. При этом точки, лежащие на прямой, могут быть заданы с использованием векторных операций в виде так называемого параметрического уравнения прямой

в котором параметр t пробегает все значения числовой прямой. Координаты точки, соответствующей некоторому значению этого параметра, определяются соотношениями

( 3.4)

Прямую в пространстве тоже можно задавать параметрическим уравнением, которое очень легко получить из предыдущего простым переходом от двумерных векторов к трехмерным. Пусть 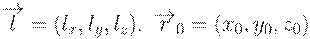. Тогда это уравнение будет определять прямую в пространстве, а координаты точек этой прямой будут определяться формулами

( 3.5)

Как известно из элементарной геометрии, через любые три точки в пространстве проходит плоскость. С другой стороны, через каждую точку плоскости можно провести единственную прямую, перпендикулярную данной плоскости. При этом все эти прямые будут параллельны друг другу, а значит, они имеют общий вектор направления. Этот вектор будем называть нормалью к плоскости. Если длина вектора равна единице, мы будем называть его единичной нормалью. В компьютерной графике часто приходится решать задачу построения нормали к некоторой плоскости, заданной тремя точками, а также задачи пересечения прямой с плоскостью и двух плоскостей.

Плоскость в пространстве можно задать, указав вектор нормали к ней и какую-либо точку, принадлежащую данной плоскости. Пусть — вектор единичной нормали, а — некоторая точка на плоскости. Тогда для любой точки , лежащей на плоскости, вектор будет ортогонален вектору нормали, а следовательно, выполняется равенство

Раскрывая это выражение в координатном виде, получаем

Теперь перепишем это уравнение в виде

( 3.6)

где . Это уравнение называется каноническим уравнением плоскости. При этом совершенно ясно, что если все это уравнение умножить на какой-либо отличный от нуля множитель, то оно будет описывать ту же самую плоскость, т.е. коэффициенты для каждой плоскости задаются с точностью до произвольного ненулевого множителя. Но если при этом вектор имеет единичную длину, то задает расстояние от начала координат до данной плоскости.

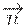
В алгоритмах компьютерной графики довольно часто приходится сталкиваться с задачей построения плоскости, проходящей через три заданные точки. Пусть три точки , и , не лежащие на одной прямой, имеют координатами и . Для канонического уравнения необходимо построить нормаль к плоскости, что легко можно осуществить, используя операцию векторного произведения. Поскольку векторы и лежат в искомой плоскости, то вектор будет ортогонален этой плоскости. Пусть , тогда уравнение плоскости будет иметь вид

Остается определить значение . Так как точка принадлежит этой плоскости, то ее координаты должны удовлетворять полученному уравнению. Подставим их в уравнение и получим

и после подстановки окончательно получим:

( 3.7)

В большинстве алгоритмов, использующих плоскости, достаточно знать нормаль к ней и какую-либо точку, принадлежащую плоскости. Очевидно, что по аналогии можно вывести каноническое уравнение прямой на плоскости, если задана нормаль к ней и принадлежащая прямой точка.

Уравнение сферы

Найдем уравнение сферы радиуса R с центром в точке O₁(x₀;y₀;z₀). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O₁(x₀;y₀;z₀) равно радиусу R, т. е. O₁M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты лю­бой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο₁ совпадает с началом координат, то уравнение сферы принимает вид .

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению не удовлетворяют никакие дей­ствительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х — любое число).

Итак, поверхность в пространстве можно задать геометрически и ана­литически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

1. Сфера задана уравнением (x – 1) 2 + y 2 + (z – 2) 2 = 9.

1. Найдите координаты центра и радиуса сферы.

2. Определите, принадлежат ли данной сфере точки А(1; 3; -1) и В(2; 2; 1).

2. Сфера с центром в точке О(0; 1; -2) проходит через точку А(-3; 1; 2).

1. Составьте уравнение сферы.

2. Найдите координаты точек оси абсцисс, принадлежащих данной сфере.

3. Точки А(1; 2; -3) и В(7; 2; 5) лежат на сфере радиуса 13. Найдите

расстояние от центра сферы до прямой АВ.

1. Сфера задана уравнением x 2 + (y +3) 2 + (z – 2) 2 = 25.

1. Найдите координаты центра и радиуса сферы.

2. Определите, принадлежат ли данной сфере точки А(4; -3; -1) и В(0; 1; 3).

2. Сфера с центром в точке О(-1; 0; 2) проходит через точку А(1; 2; 1).

1. Составьте уравнение сферы.

2. Найдите координаты точек оси ординат, принадлежащих данной сфере.

3. Точки А(1; 5; 6) и В(1; -1; -2) лежат на сфере, центр которой удален от

середины отрезка АВ на 12. Найдите радиус сферы.

1. Сфера задана уравнением x 2 + y 2 + z 2 + 2y – 4z = 4.

a) Найдите координаты центра и радиуса сферы.

b) Найдите значение m, при котором точки А(0; m; 2) и

В(1; 1; m — 2) принадлежат данной сфере.

2. Диаметр сферы – отрезок АВ с концами А(2; -1; 4) и В(2; 7; 10).

a) Составьте уравнение сферы.

b) Найдите кратчайшее расстояние от точки данной сферы до плоскости Оxy.

3. Сфера задана уравнением (x + 3) 2 + (y – 4) 2 + (z + 1) 2 = 25. Найдите

длину линии, по которой данная сера пересекается с плоскостью Оyz.