Уроки по математике уравнение прямой на плоскости

Уравнение прямой, виды уравнения прямой на плоскости

В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.

Определение уравнения прямой на плоскости

Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат O х у .

Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе O x y , называется уравнением прямой на плоскости.

Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.

Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.

Общее уравнение прямой линии

Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат O x y .

Уравнение вида A x + B y + C = 0 , где x и y – переменные, а А , В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат O x y . В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида A x + B y + C = 0 .

Таким образом, общее уравнение прямой на плоскости имеет вид A x + B y + C = 0 .

Поясним некоторые важные аспекты темы.

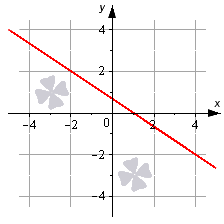
Посмотрите на рисунок.

Линия на чертеже определяется уравнением вида 2 x + 3 y — 2 = 0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2 x + 3 y — 2 = 0 , дают нам прямую линию, которую мы видим на рисунке.

Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А , В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида A x + B y = 0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение A x + B y + C = 0 задает прямую, расположенную параллельно оси абсцисс O x . Если B равно нулю, то линия параллельна оси ординат O y .

Вывод: при некотором наборе значений чисел А , В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат O х у .

Прямая, заданная уравнением вида A x + B y + C = 0 , имеет нормальный вектор прямой с координатами A , B .

Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.

Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.

Уравнение прямой в отрезках

Уравнение прямой в отрезках имеет вид x a + y b = 1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.

Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a , 0 и 0 , b , а затем соединить их прямой линией.

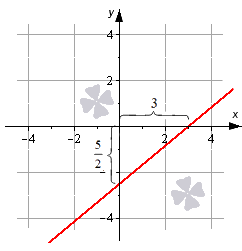
Построим прямую, которая задана формулой x 3 + y — 5 2 = 1 . Отмечаем на графике две точки 3 , 0 , 0 , — 5 2 , соединяем их между собой.

Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».

Уравнение прямой с угловым коэффициентом

Эти уравнения, имеющие вид y = k · x + b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x .

Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси O x .

Для обозначения угла наклона прямой к положительному направлению оси O x в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси O x или совпадает с ней.

Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k = t g α . Для прямой, которая располагается параллельно оси O y или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).

Прямая, которая задана уравнением y = k · x + b , проходит через точку 0 , b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y = k · x + b , задает на плоскости прямую линию, которая проходит через точку 0 , b и образует угол α с положительным направлением оси O x , причем k = t g α .

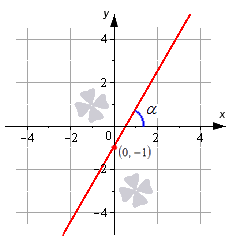
Изобразим прямую линию, которая определяется уравнением вида y = 3 · x — 1 .

Эта линия должна пройти через точку ( 0 , — 1 ) . Угол наклона α = a r c t g 3 = π 3 равен 60 градусов к положительному направлению оси O x . Угловой коэффициент равен 3

Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.

Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.

Каноническое уравнение прямой на плоскости

Данный вид уравнения имеет вид x — x 1 a x = y — y 1 a y , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не равны нулю.

Прямая линия, заданная каноническим уравнением прямой, проходит через точку M 1 ( x 1 , y 1 ) . Числа a x и a y в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x — x 1 a x = y — y 1 a y в декартовой системе координат O x y соответствует линии, проходящей через точку M 1 ( x 1 , y 1 ) и имеющей направляющий вектор a → = ( a x , a y ) .

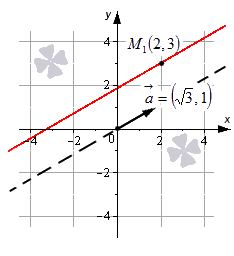
Изобразим в системе координат O x y прямую линию, которая задается уравнением x — 2 3 = y — 3 1 . Точка M 1 ( 2 , 3 ) принадлежит прямой, вектор a → ( 3 , 1 ) является направляющим вектором этой прямой линии.

Каноническое уравнение прямой линии вида x — x 1 a x = y — y 1 a y может быть использовано в случаях, когда a x или a y равно нулю. Наличие ноля в знаменателе делает запись x — x 1 a x = y — y 1 a y условной. Уравнение можно записать следующим образом a y ( x — x 1 ) = a x ( y — y 1 ) .

В том случае, когда a x = 0 , каноническое уравнение прямой принимает вид x — x 1 0 = y — y 1 a y и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.

Каноническое уравнение прямой при условии, что a y = 0 , принимает вид x — x 1 a x = y — y 1 0 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.

Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.

Параметрические уравнения прямой на плоскости

Данные уравнения имеют вид x = x 1 + a x · λ y = y 1 + a y · λ , где x 1 , y 1 , a x , a y — это некоторые действительные числа, из которых a x и a y не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.

Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .

Числа x , y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .

Предположим, что λ = 0 .

Тогда x = x 1 + a x · 0 y = y 1 + a y · 0 ⇔ x = x 1 y = y 1 , т. е. точка с координатами ( x 1 , y 1 ) принадлежит прямой.

Обращаем ваше внимание на то, что коэффициенты a x и a y при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.

Рассмотрим параметрические уравнения прямой линии вида x = 2 + 3 · λ y = 3 + λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку ( x 1 , y 1 ) и имеет направляющий вектор a → = ( 3 , 1 ) .

Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».

Нормальное уравнение прямой

Нормальное уравнение прямой имеет вид , A x + B y + C = 0 , где числа А , В , и C таковы, что длина вектора n → = ( A , B ) равна единице, а C ≤ 0 .

Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат O х у , является вектор n → = ( A , B ) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n → = ( A , B ) .

Еще одним вариантом записи нормального уравнения прямой линии является cos α · x + cos β · y — p = 0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n → = ( cos α , cos β ) , справедливо равенство n → = cos 2 α + cos 2 β = 1 , величина p ≥ 0 и равна расстоянию от начала координат до прямой.

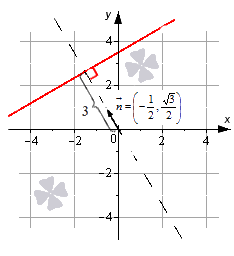
Рассмотрим общее уравнение прямой — 1 2 · x + 3 2 · y — 3 = 0 . Это общее уравнение прямой является нормальным уравнением прямой, так как n → = A 2 + B 2 = — 1 2 2 + 3 2 = 1 и C = — 3 ≤ 0 .

Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты — 1 2 , 3 2 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n → = — 1 2 , 3 2 .

Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.

Если в общем уравнении прямой A x + B y + C = 0 числа А , В и С таковы, что уравнение A x + B y + C = 0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».

Конспект занятия по теме «Различные уравнения прямой на плоскости»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Различные виды уравнения прямой на плоскости

1 Общее уравнение прямой на плоскости имеет вид

2 Уравнение прямой с угловым коэффициентом записывается в виде

,

где , — угол, который прямая образует с положительным направлением оси ОХ, — ордината точки пересечения прямой с осью ОУ.

3 Уравнение прямой , проходящей через данную точку в данном направлении имеет вид

,

где , — угол, который прямая образует с положительным направлением оси ОХ.

.

5 Уравнение прямой в отрезках имеет вид

,

где и — длины отрезков (с учетом знаков), отсекаемых прямой на осях ОХ и ОУ соответственно.

6 Угол между прямыми на плоскости

Пусть даны две прямые и .

Тангенс угла между прямыми и вычисляют по формуле

.

7 Условие параллельности прямых на плоскости

.

8 Условие перпендикулярности прямых на плоскости

.

9 Расстояние от точки М ₀ (х ₀ ; у ₀ ) до прямой Ах + Ву + С = 0 определяется по формуле

.

Решение типового примера:

Даны координаты вершин Δ АВС А(-2;2), В(1;6), С(2;4).

1) длину стороны АВ;

2) уравнения сторон АВ и ВС и их угловые коэффициенты;

3) внутренний угол В;

4) уравнение медианы АЕ;

5) уравнение и длину высоты С D ;

6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М, её пересечение с высотой С D .

1) Расстояние d между точками А( x ₁ ; y ₁ ) и В( x _2; y ₂ ) определяется по формуле .

Воспользовавшись ей, находим длину стороны АВ

= = = 5.

2) Уравнение прямой, проходящей через две заданные точки плоскости и имеет вид: .

Поэтому АВ: .

Угловой коэффициент k прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом: .

откуда .

Найдем уравнение прямой ВС

; ;

(ВС).

Приведем к виду : ; .

3) Для определения В треугольника АВС воспользуемся формулой

.

;

, .

4) Для составления уравнения медианы АЕ найдем координаты точки Е – середины стороны ВС по формулам: ; .

; ; .

Уравнение медианы АЕ:

А(-2;2), Е .

(АЕ).

5) Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку М ₀ с заданным угловым коэффициентом k и условием перпендикулярности прямых АВ и CD которая выражается соотношением , откуда .

С (2; 4); .

Для вычисления длины высоты CD воспользуемся формулой отыскания расстояния d от заданной точки М ₀ до заданной прямой с уравнением , .

.

6) Искомая прямая , поэтому .

Подставив в уравнение вместо х ₀ , у ₀ координаты точки , вместо значение получим уравнение прямой EF .

( EF ).

Найдем координаты точки М – пересечения прямых EF и CD . Для этого решим систему:

;

Таким образом .

Задание Даны координаты вершин треугольника АВС. Найти:

1) длину стороны АВ

2) уравнения сторон АВ и ВС и их угловые коэффициенты

3) внутренний угол В в радианах с точностью до 0,01

4) уравнение медианы АЕ; 5) уравнение и длину высоту С D

6) уравнение прямой, проходящей через точку Е параллельно стороне АВ и точку М ее пересечения с высотой С D

План занятия «Уравнение прямой на плоскости»

Просмотр содержимого документа
«План занятия «Уравнение прямой на плоскости»»

Министерство образования Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение «Ставропольский региональный многопрофильный колледж»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА ЗАНЯТИЯ ПО ТЕМЕ

«УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ»

ЕН.01 ЭЛЕМЕНТЫ ВЫСШЕЙ

09.02.03 Программирование в компьютерных сетях

Иванова Владлена Сергеевна

Методическая разработка занятия

Специальность: 09.02.03 Программирование в компьютерных сетях

Преподаватель: Иванова Владлена Сергеевна

Дисциплина: ЕН.01 Элементы высшей математики

Наименование раздела: Элементы аналитической геометрии

Тема занятия: Уравнения прямой на плоскости

Вид: Практическое занятие

Тип занятия: Повторение и закрепление

Цель занятие: составить различные виды уравнений прямой на плоскости.

ПК 1.1. Выполнять разработку спецификаций отдельных компонент

ОК 2. Организовывать собственную деятельность, определять методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Требования к умениям (практическому опыту): студент должен уметь составлять уравнения прямой на плоскости следующих видов: общее уравнение прямой; уравнение прямой в отрезках; уравнение с угловым коэффициентом; уравнение в канонической форме; уравнение прямой, проходящей через две данные точки; параметрические уравнения; нормальное уравнение. Разработать алгоритм составления уравнения прямой на плоскости.

Цели самостоятельной работы: формирование умения продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности.

Фронтальная работа (работа в группах и индивидуально)

Обсуждение деталей схематического изображения

Методы и приемы обучения: словесные, наглядные, информационные, компьютерные, объяснительно-иллюстративные, метод алгоритмических предписаний, мозговой штурм, прием «Ромашка Блума», рефлексия, прием из кинезиологического комплекса «Зеркальное рисование».

карточки для самостоятельной работы;

задания для выполнения на уроке;

задания для самопроверки;

Организационный момент (5 мин.)

Взаимные приветствия преподавателя и студентов; фиксация отсутствующих в учебном журнале; проверка внешнего состояния кабинета.

Проверка подготовленности студентов к занятию, их настроя на работу. Инструктирование по работе с оценочным листом (в котором в ходе работы оценивается работа каждой пары (за каждый правильный ответ студент получает наклейку «лайк». Оценка ставится паре, набравшей необходимое количество «лайков». 3 наклейки – удовлетворительно, 4 наклейки – хорошо, 6 наклеек – отлично)

САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ

1.Актуализация опорных знаний (35 мин.)

ЗАДАНИЕ №1. (Время выполнения – 5 мин.)

Закрепление знаний предыдущей темы «Основы алгебры векторов» с использованием приема – поиск соответствий.

Правильно соотнести определение и формулу: орт; модуль (длина) вектора; скалярное произведение векторов.

ЗАДАНИЕ №2. (Время выполнения – 15 мин.)

Повторение основных понятий лекции «Уравнения прямой на плоскости» с использованием приема «Ромашка Блума» (Студенты работают в парах. За каждый правильный ответ пара получает по «лайку»)

1 лепесток: Что мы изучили на прошлой лекции? Что называют уравнением прямой на плоскости?

2 лепесток: Какие именно виды уравнений прямой на плоскости мы изучили?

3 лепесток: Почему нормальное уравнение прямой так называется?

4 лепесток: Всегда ли общее уравнение прямой на плоскости проходит через начало координат?

5 лепесток: Что будет, если общее уравнение прямой на плоскости разделить на –С?

6лепесток: Как вы найдете расстояние от точки до прямой?

ЗАДАНИЕ №3. (Время выполнения – 3 мин.)

Проведение упражнения из кинезиологического комплекса «Зеркальное рисование».

Необходимо положить на стол чистый лист бумаги. Студенты рисуют одновременно обеими руками зеркально-симметричные рисунки (квадраты, треугольники, горизонтальные линии), буквы. При выполнении этого упражнения они почувствуют, как расслабляются глаза и руки. Когда деятельность обоих полушарий синхронизируется, заметно увеличится эффективность работы всего мозга.

Прослушать подготовленное студентами мини-сообщение на тему:

взаимное расположение прямых в пространстве: пересекающиеся прямые, параллельные прямые, скрещивающиеся прямые.

Решить задачу: сторона АС треугольника АВС параллельно плоскости а, а его стороны пересекают плоскость в точках M и N. Доказать, что треугольник АВС и MBN подобны.

2.Решение практических задач (Время выполнения – 42 мин.)

Игра «Моя геометрия». Алгоритм игры:

На экране появляется таблица (9 ячеек) с разной «стоимостью» задания (1 «лайк», 2 «лайка», 3 «лайка»)

Студенты выбирают «стоимость» и получают задание, которое нужно решить.

Если задание было решение у доски в полной мере, студент получает определенное количество лайков.

1 лайк (Составить общее уравнение прямой на плоскости)

3 лайка (Составить уравнение прямой, проходящей через две данные точки

3 лайка (Составить уравнение в параметрической форме)

2 лайка (Составить уравнение прямой в отрезках)

1 лайк (Составить неполное уравнение общей прямой)

2 лайка (Составить уравнение с угловым коэффициентом)

3 лайка (Составить уравнение прямой в каноничной форме)

3 лайка (Составить нормальное уравнение в прямой)

1 лайк (Найти расстояние между прямой и точкой)