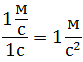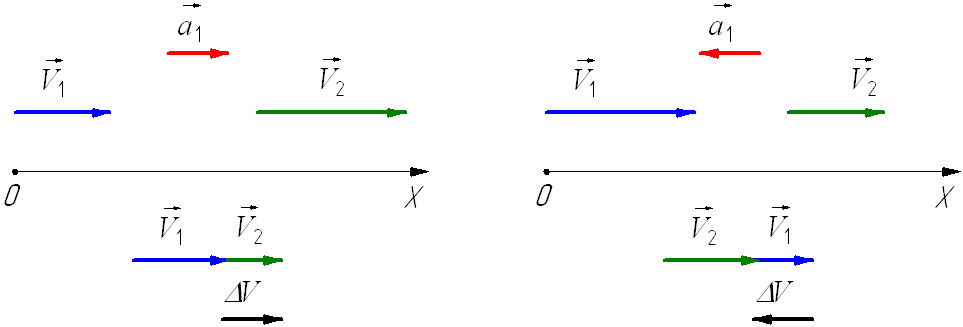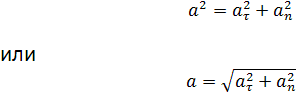Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
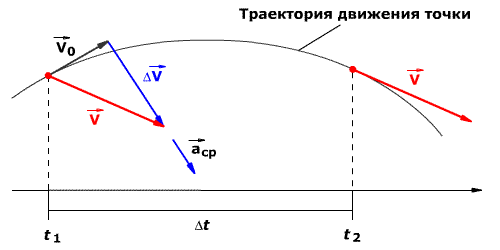
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 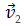
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
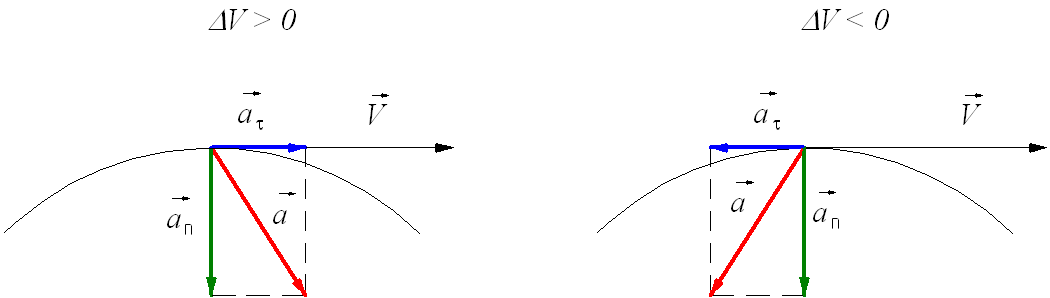
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 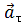
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 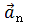
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Ускорение тела
Ускорением тела называют векторную величину показывающую быстроту изменения скорости движения тела. Обозначают ускорение как $\overline$.
Среднее ускорение тела
Допустим, что в моменты времени $t$ и $t+\Delta t$ скорости равны $\overline
\[\Delta \overline
тогда среднее ускорение тела равно:
Мгновенное ускорение тела
Устремим промежуток времени $\Delta t$ к нулю, тогда из уравнения (2) получим:
Формула (3) является определением мгновенного ускорения. Принимая во внимание, что в декартовой системе координат:
\[\overline
Из выражения (6) следует, что проекции ускорения на оси координат (X,Y,Z) равны:
При этом модуль ускорения найдем в соответствии с выражением:
Для выяснения вопроса о направлении ускорения движения тела Вектор скорости представим как:
где $v$ — модуль скорости тела; $\overline<\tau >$ — единичный вектор касательный к траектории движения материальной точки. Подставим выражение (8) в определение мгновенной скорости, получим:
Единичный касательный вектор $\overline<\tau >$ определяется точкой траектории, которая в свою очередь характеризуется расстоянием ($s$) от начальной точки. Значит вектор $\overline<\tau >$ — это функция от $s$:
Параметр $s$ — функция от времени. Получаем:
где вектор $\overline<\tau >$ по модулю не изменяется. Это означает, что вектор $\frac
Величина $\left|\frac
И так мы получили:
Принимая во внимание, что $\frac
Выражение (13) показывает, что полное ускорение тела состоит из двух компонент, которые взаимно перпендикулярны. Тангенциального ускорения ($<\overline>_<\tau >$), направленного по касательной к траектории движения и равного:
Модуль полного ускорения равен:
Единицей измерения ускорения в Международной системе единиц (СИ) является метр на секунду в квадрате:
Прямолинейное движение тела
Если траекторией движения материальной точки является прямая, то вектор ускорения направлен вдоль той же прямой, что и вектор скорости. Изменяется только величина скорости.
Переменное движение называют ускоренным, если скорость материальной точки постоянно увеличивается по модулю. При этом $a>0$, векторы ускорения и скорости сонаправлены.
Если скорость по модулю убывает, то движение называют замедленным ($a Пример 1
Задание: Движения двух материальных точек заданы следующими кинематическими уравнениями: $x_1=A+Bt-Ct^2$ и $x_2=D+Et+Ft^2,$ чему равны ускорения этих двух точек в момент времени, когда равны их скорости, если $A$, B,C,D,E.F — постоянные большие нуля.
Решение: Найдем ускорение первой материальной точки:
У второй материальной точки ускорение будет равно:
Мы получили, что точки движутся с постоянными ускорениями, которые не зависят от времени, поэтому момент времени, в который скорости равны, искать не обязательно.
Ответ: $a_1=-2С\frac<м><с^2>$, $a_2=2F\frac<м><с^2>$
Задание: Движение материальной точки задано уравнением: $\overline
Решение: Рассмотрим уравнение движения нашей точки:
В координатной записи уравнению (2.1) соответствует система уравнений:
Возведем в квадрат каждое уравнение системы (2.2) и сложим их:
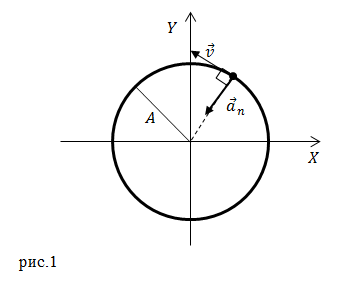
Мы получили уравнение окружности радиуса $A$ (рис.1).
Величину центростремительного ускорения, учитывая, что радиус траектории равен А, найдем как:
Проекции скорости на оси координат равны:
Величина скорости равна:
Подставим результат (2.6) в (2.4), нормальное ускорение равно:
Легко показать, что движение точки в нашем случае является равномерным движением по окружности и полное ускорение точки равно центростремительному ускорению. Для этого можно взять производную от проекций скоростей (2.5) по времени и используя выражение:
Скорость. Ускорение. Равноускоренное прямолинейное движение
1. Реальное механическое движение — это движение с изменяющейся скоростью. Движение, скорость которого стечением времени изменяется, называют неравномерным движением.
При неравномерном движении координату тола уже нельзя определить но формуле \( x=x_0+v_xt \) , так как значение скорости движения не является постоянным. Поэтому для характеристики быстроты изменения положения тела с течением времени при неравномерном движении вводят величину, называемую средней скоростью.
Средней скоростью \( \vec\) тела ко времени \( t \) , за которое оно произошло: \( \vec
Записанная формула определяет среднюю скорость как векторную величину. В практических целях этой формулой можно воспользоваться для определения модуля средней скорости лишь в том случае, когда тело движется вдоль прямой в одну сторону. Если же нужно определить среднюю скорость движения автомобиля от Москвы до Санкт-Петербурга и обратно, чтобы рассчитать расход бензина, то эту формулу применить нельзя, поскольку перемещение в этом случае равно нулю и средняя скорость тоже равна нулю. Поэтому на практике при определении средней скорости пользуются величиной, равной отношению пути \( l \) ко времени \( t \) , за которое этот путь пройден: \( v_<ср>=\frac
2. Важно, что, зная среднюю скорость неравномерного движения на каком-либо участке траектории, нельзя определить положение тела на этой траектории в любой момент времени. Например, если средняя скорость движения автомобиля за 2 часа 50 км/ч, то мы не можем сказать, где он находился через 0,5 часа от начала движения, через 1 час, 1,5 часа и т.п., поскольку он мог первые полчаса двигаться со скоростью 80 км/ч, затем какое-то время стоять, а какое-то время ехать в пробке со скоростью 20 км/ч.
3. Двигаясь по траектории, тело проходит последовательно все её точки. В каждой точке траектории оно находится в определённые моменты времени и имеет какую-то скорость.
Мгновенной скоростью называют скорость тела в данный момент времени в данной точке траектории.
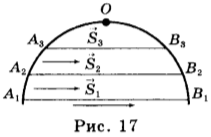
Предположим, некоторое тело совершает неравномерное прямолинейное движение (рис. 17), его скорость в точке О можно определить следующим образом: выделим на траектории участок AB, внутри которого находится точка О. Перемещение тела на этом участке — \( \vec_1 \) совершено за время \( t_1 \) . Средняя скорость движения на этом участке – \( \vec_2 \) , а время движения — \( t_2 \) . Тогда средняя скорость за это время: \( \vec
При дальнейшем уменьшении перемещения и соответственно времени движения тела они станут такими маленькими, что прибор, например спидометр, перестанет фиксировать изменение скорости, и движение за этот малый промежуток времени можно считать равномерным. Средняя скорость на этом участке и есть мгновенная скорость тела в т.О.
Таким образом, мгновенной скоростью называют векторную физическую величину, равную отношению малого перемещения ( \( \Delta<\vec> \) ) к малому промежутку времени \( \Delta><\Delta
4. Одним из видов неравномерного движения является равноускоренное движение. Равноускоренным движением называют движение, при котором скорость тела за любые равные промежутки времени изменяется на одно и то же значение.
Слова «любые равные промежутки времени» означают, что какие бы равные промежутки времени (2 с, 1 с, доли секунды и т.п.) мы ни взяли, скорость всегда будет изменяться одинаково. При этом её модуль может как увеличиваться, так и уменьшаться.
5. Характеристикой равноускоренного движения, помимо скорости и перемещения, является ускорение.
Пусть в начальный момент времени \( t_0=0 \) скорость тела равна \( \vec
Ускорение тела при равноускоренном движении — векторная физическая величина, равная отношению изменения скорости тела к промежутку времени, за который это изменение произошло.
Единица ускорения \( [a]=[v]/[t] \) ; \( [a] \) = 1 м/с/1 с = 1 м/с 2 . 1 м/с 2 — это такое ускорение, при котором скорость тела изменяется за 1 с на 1 м/с.
Направление ускорения совпадает с направлением скорости движения, если модуль скорости увеличивается, ускорение направлено противоположно скорости движения, если модуль скорости уменьшается.
6. Преобразовав формулу ускорения, можно получить выражение для скорости тела при равноускоренном движении: \( \vec
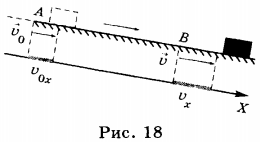
Чтобы определить значение скорости равноускоренного движения в любой момент времени, следует записать уравнение для проекции скорости на ось ОХ. Оно имеет вид: \( v_x = v_ <0x>+ a_xt \) ; если \( v_<0x>=0 \) , то \( v_x = a_xt \) .
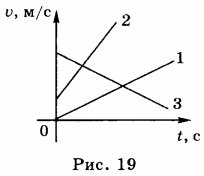
7. Как видно из формулы скорости равноускоренного движения, она линейно зависит от времени. Графиком зависимости модуля скорости от времени является прямая, составляющая некоторый угол с осью абсцисс (осью времени). На рисунке 19 приведены графики зависимости модуля скорости от времени.
График 1 соответствует движению без начальной скорости с ускорением, направленным так же, как и скорость; график 2 — движению с начальной скоростью \( v_ <02>\) и с ускорением, направленным так же, как и скорость; график 3 — движению с начальной скоростью \( v_ <03>\) и с ускорением, направленным в сторону, противоположную направлению скорости.
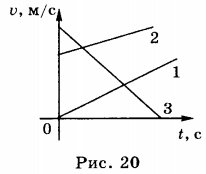
8. На рисунке приведены графики зависимости проекции скорости равноускоренного движения от времени (рис. 20).
График 1 соответствует движению без начальной скорости с ускорением, направленным вдоль положительного направления оси X; график 2 — движению с начальной скоростью \( v_ <02>\) , с ускорением и скоростью, направленными вдоль положительного направления оси X; график 3 — движению с начальной скоростью \( v_ <03>\) : до момента времени \( t_0 \) направление скорости совпадает с положительным направлением оси X, ускорение направлено в противоположную сторону. В момент времени \( t_0 \) скорость равна нулю, а затем и скорость, и ускорение направлены в сторону, противоположную положительному направлению оси X.
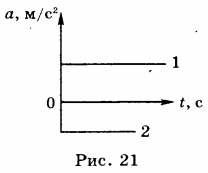
9. На рисунке 21 приведены графики зависимости проекции ускорения равноускоренного движения от времени.
График 1 соответствует движению, проекция ускорения которого положительна, график 2 — движению, проекция ускорения которого отрицательна.
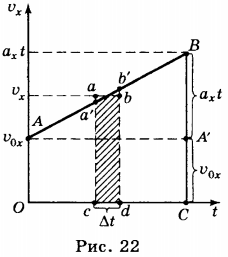
10. Формулу перемещения тела при равноускоренном движении можно получить, используя график зависимости проекции скорости этого движения от времени (рис. 22).
Выделим на графике малый участок \( ab \) и опустим перпендикуляры из точек \( a \) и \( b \) на ось абсцисс. Если промежуток времени \( \Delta
На такие полоски можно разбить всю фигуру ОАВС, и её площадь равна сумме площадей всех полосок. Следовательно, проекция перемещения тела за время \( t \) численно равна площади трапеции ОАВС. Площадь трапеции равна произведению полусуммы её оснований на высоту: \( S_x= \frac<1><2>(OA+BC)OC \) .
Как видно из рисунка, \( OA=v_<0x>,BC=v_x,OC=t \) . Отсюда следует, что проекция перемещения выражается формулой \( S_x= \frac<1><2>(v_<0x>+v_x)t \) . Так как \( v_x = v_ <0x>+ a_
Полученная формула позволяет определить положение (координату) тела в любой момент времени, если известны начальная скорость, начальная координата и ускорение.
11. На практике часто используют формулу или \( v^2_x-v^2_<0x>=2a_xs_x \) , или \( v^2-v^2_<0>=2as \) .
Если начальная скорость тела равна нулю, то: \( v^2_x=2a_xs_x \) .
Полученная формула позволяет рассчитать тормозной путь транспортных средств, т.е. путь, который проезжает, например, автомобиль до полной остановки. При некотором ускорении движения, которое зависит от массы автомобиля и силы тяги двигателя, тормозной путь тем больше, чем больше начальная скорость автомобиля.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
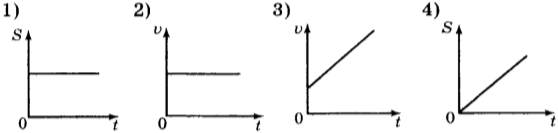
1. Hа рисунке приведены графики зависимости пути и скорости тела от времени. Какой график соответствует равноускоренному движению?
2. Автомобиль, начав двигаться из состояния покоя но прямолинейной дороге, за 10 с приобрел скорость 20 м/с. Чему равно ускорение автомобиля?
1) 200 м/с 2
2) 20 м/с 2
3) 2 м/с 2
4) 0,5 м/с 2
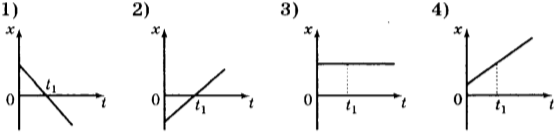
3. На рисунках представлены графики зависимости координаты от времени для четырёх тел, движущихся вдоль оси \( Оx \) . У какого из тел в момент времени \( t_1 \) скорость движения равна нулю?
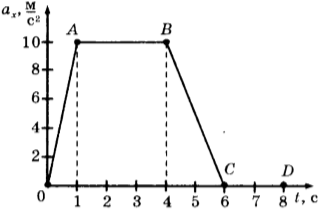
4. На рисунке представлен график зависимости проекции ускорения от времени для тела, движущегося прямолинейно вдоль оси \( Оx \) .
Равноускоренному движению соответствует участок
1) только ОА
2) только АВ
3) только ОА и ВС
4) только CD
5. При изучении равноускоренного движения измеряли путь, пройденный телом из состояния покоя за последовательные равные промежутки времени (за первую секунду, за вторую секунду и т.д.). Полученные данные приведены в таблице.
Чему равен путь, пройденный телом за третью секунду?
1) 4 м
2) 4,5 м
3) 5 м
4) 9 м
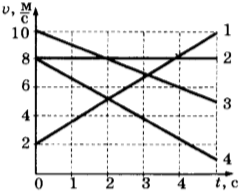
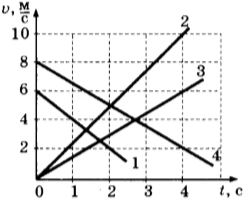
6. На рисунке представлены графики зависимости скорости движения от времени для четырёх тел. Тела движутся по прямой.
Для какого(-их) из тел — 1, 2, 3 или 4 — вектор ускорения направлен противоположно вектору скорости?
1) только 1
2) только 2
3) только 4
4) 3 и 4
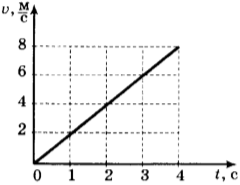
7. Используя график зависимости скорости движения тела от времени, определите его ускорение.
1) 1 м/с 2
2) -1 м/с 2
3) 2 м/с 2
4) -2 м/с 2
8. При изучении равноускоренного движения измеряли скорость тела в определённые моменты времени. Полученные данные, приведены в таблице. Чему равна скорость тела в момент времени 3 с?
1) 0 м/с
2) 2 м/с
3) 4 м/с
4) 14 м/с
9. На рисунке приведены графики зависимости скорости движения четырёх тел от времени. Ускорение какого из тел равно -1,5 м/с?
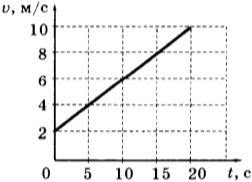
10. Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 30-й секунды. Считать, что характер движения тела не изменился.
1) 14 м/с
2) 20 м/с
3) 62 м/с
4) 69,5 м/с
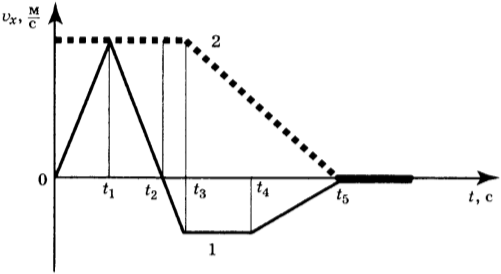
11. Два тела движутся по оси \( Оx \) . На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) В промежутке времени \( t_3-t_5 \) тело 2 движется равноускоренно.
2) К моменту времени \( t_2 \) от начала движения тела прошли одинаковые пути.
3) В промежутке времени \( 0-t_3 \) тело 2 находится в покое.
4) В момент времени \( t_5 \) тело 1 останавливается.
5) В промежутке времени \( t_3-t_4 \) ускорение \( a_x \) тела 1 отрицательно.
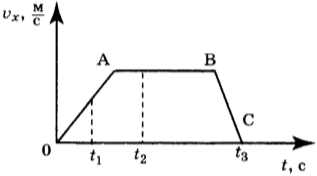
12. На рисунке представлен график зависимости проекции скорости от времени для тела, движущегося вдоль оси Ох.
Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) Участок ОА соответствует ускоренному движению тела.
2) Участок АВ соответствует состоянию покоя тела.
3) В момент времени \( t_1 \) тело имело максимальное по модулю ускорение.
4) Момент времени \( t_3 \) соответствует остановке тела.
5) В момент времени \( t_2 \) тело имело максимальное по модулю ускорение.
Часть 2
13. Зависимость координаты от времени для некоторого тела описывается уравнением \( x=12t-t^2 \) . В какой момент времени скорость движения равна нулю?
http://www.webmath.ru/poleznoe/fizika/fizika_96_uskorenie_tela.php
http://fizi4ka.ru/ogje-2018-po-fizike/skorost-uskorenie-ravnouskorennoe-prjamolinejnoe-dvizhenie.html