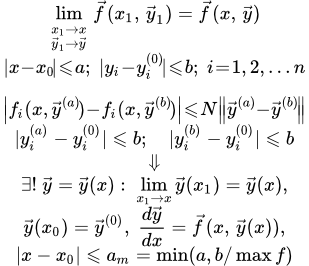Условие липшица в дифференциальных уравнениях

Теорема существования и единственности решения системы дифференциальных уравнений

Здесь мы рассматриваем теорему существования и единственности решения системы дифференциальных уравнений с неизвестными функциями от переменной :
(1.1) ;
(1.2) ;
.
(1.n) .

Формулировка и доказательство этой теоремы является непосредственным обобщением теоремы для уравнения первого порядка, которое рассмотрено на странице “Теорема существования и единственности решения ДУ первого порядка”.

Векторная форма записи

Поскольку уравнения (1.1) – (1.n) однотипны, то мы применим векторную форму записи. Это позволит сократить объем выкладок и сделает доказательство более ясным.

Совокупность неизвестных функций мы будем обозначать одним вектором . Совокупность функций от независимой переменной и от зависимых функций мы обозначим как
.

То есть совокупность из величин мы будем обозначать вектором . Равенство

будет обозначать систему из уравнений:
,
где .

Под нормой вектора мы будем понимать сумму модулей его компонент:
.

Формулировка теоремы

Пусть дана система дифференциальных уравнений:
(1)
с начальными условиями
(1.0) .
Пусть – непрерывных функций от переменных в замкнутой области :

и, следовательно, ограничены некоторым положительным значением :
(2) .
И пусть функции удовлетворяют в области условию Липшица:
(3) ,
где – положительное число.
Тогда существует единственное решение системы (1):
,
удовлетворяющее начальным условиям , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Условие Липшица имеет вид:
(3) .
или в развернутом виде:
(3.1) ,
где – положительное число;
, и – любые значения из области .

Если условие Липшица выполняется и в некоторой точке существует частная производная , то она ограничена по модулю значением .
Для доказательства положим в (3.1) для всех . Тогда (3.1) примет вид:
.
Перейдем к пределу :
.

Если в области функции имеют непрерывные частные производные , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частные производные непрерывны в замкнутой области, то они ограничены:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой компоненты принадлежат интервалам между и :
.
Тогда:

.

Доказательство существования решения

Приведем исходную систему (1) с начальными условиями (1.0) к системе интегральных уравнений. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем каждое уравнение по от до :
;
Подставим начальные условия . В результате получим систему интегральных уравнений:
(4) .

Покажем, что система интегральных уравнений (4) эквивалентна дифференциальным уравнениям (1) с начальными условиями (1.0). Для этого нужно показать, что из (1) и (1.0) следует (4) и из (4) следует (1) и (1.0). То, что из (1) и (1.0) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.0). Для этого подставим в (4) . Получим начальные условия (1.0). Продифференцировав обе части системы (4) по , получаем (1).

Далее мы пытаемся найти решение уравнений (4) с помощью последовательных приближений. Для этого определяем ряд векторов функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.m) .
Функции непрерывны, потому что интеграл есть непрерывная функция от верхнего предела. Мы предполагаем, что при , стремится к решению системы (4):
(6) ,
где – решение системы (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет системе (4):
.

1) Доказательство существования предела y (m) при m стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.m) к суммам рядов. Для этого пишем:

.
Таким образом нам нужно доказать, что ряды
(7)
сходятся при .

Сначала покажем, что при , компоненты последовательных приближений принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежит интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7).

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .

Далее применим метод индукции. Пусть
(8.m) .
Тогда

;
(8.m+1) .
Итак, поскольку (8.m) справедливо для и из (8.m) следует (8.m+1), то (8.m) выполняется для любых .

Запишем -й ряд (7) в виде:
(7.i) ,
где .
Применим (8.m) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.i), кроме первого, ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.i), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.i) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.i) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.m):
(5.m) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.m) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.m):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
(12) .
Пусть есть наибольшее из чисел . Тогда (12) выполняется для всех и для всех .
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.m) .
принимает вид
(11) .

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Тогда .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

.
Итак, мы получили оценку:
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 20-06-2016

Основные понятия и определения дифференциальных уравнений

Дифференциальным уравнением называется уравнение, связывающее независимую переменную , искомую функцию и её производные , т. е. уравнение вида

Если искомая функция есть функция одной независимой переменной , дифференциальное уравнение называется обыкновенным ; например,

Когда искомая функция есть функция двух и более независимых переменных, например, если , то уравнение вида

называется уравнением в частных производных. Здесь — неотрицательные целые числа, такие, что ; например

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение — уравнение первого порядка, дифференциальное уравнение , где — известная функция, — уравнение второго порядка; дифференциальное уравнение — уравнение 9-го порядка.

Решением дифференциального уравнения n-го порядка на интервале называется функция , определенная на интервале вместе со своими производными до n-го порядка включительно, и такая, что подстановка функции в дифференциальное уравнение превращает последнее в тождество по на . Например, функция является решением уравнения на интервале . В самом деле, дифференцируя функцию дважды, будем иметь

Подставляя выражения и в дифференциальное уравнение, получим тождество

График решения дифференциального уравнения называется интегральной кривой этого уравнения.

Общий вид уравнения первого порядка

Если уравнение (1) удается разрешить относительно , то получится уравнение первого порядка, разрешенное относительно производной.

Задачей Коши называют задачу нахождения решения уравнения , удовлетворяющего начальному условию (другая запись ).

Геометрически это означает, что ищется интегральная кривая, проходящая через заданную точку плоскости (рис. 1).

Теорема существования и единственности решения задачи Коши

Пусть дано дифференциальное уравнение , где функция определена в некоторой области плоскости , содержащей точку . Если функция удовлетворяет условиям

а) есть непрерывная функция двух переменных и в области ;

б) имеет частную производную , ограниченную в области , то найдется интервал , на котором существует единственное решение данного уравнения, удовлетворяющее условию .

Теорема дает достаточные условия существования единственного решения задачи Коши для уравнения , но эти условия не являются необходимыми . Именно, может существовать единственное решение уравнения , удовлетворяющее условию , хотя в точке не выполняются условия а) или б) или оба вместе.

1. . Здесь . В точках оси условия а) и б) не выполняются (функция и её частная производная разрывны на оси и неограниченны при ), но через каждую точку оси проходит единственная интегральная кривая (рис. 2).

2. . Правая часть уравнения и ее частная производная непрерывны по и во всех точках плоскости . В силу теоремы существования и единственности областью, в которой данное уравнение имеет единственное решение
является вся плоскость .

3. . Правая часть уравнения определена и непрерывна во всех точках плоскости . Частная производная обращается в бесконечность при , т.е. на оси , так что при нарушается условие б) теоремы существования и единственности. Следовательно, в точках оси возможно нарушение единственности. Легко проверить, что функция есть решение данного уравнения. Кроме этого, уравнение имеет очевидное решение . Таким образом, через каждую точку оси проходит по крайней мере две интегральные линии и, следовательно, действительно в точках этой оси нарушается единственность (рис. 3).

Интегральными линиями данного уравнения будут также линии, составленные из кусков кубических парабол и отрезков оси , например, и др., так что через каждую точку оси проходит бесконечное множество интегральных линий.

Условие Липшица

Замечание. Условие ограниченности производной , фигурирующее в теореме существования и единственности решения задачи Коши, может быть несколько ослаблено и заменено так называемым условием Липшица .

Говорят, что функция , определенная в некоторой области , удовлетворяет в условию Липшица по , если существует такая постоянная ( постоянная Липшица ), что для любых из и любого из справедливо неравенство

Существование в области ограниченной производной достаточно для того, чтобы функция удовлетворяла в условию Липшица. Напротив, из условия Липшица не вытекает условие ограниченности ; последняя может даже не существовать. Например, для уравнения функция не дифференцируема по в точке , но условие Липшица в окрестности этой точки выполняется. В самом деле,

поскольку а . Таким образом, условие Липшица выполняется с постоянной .

Теорема. Если функция непрерывна и удовлетворяет условию Липшица по в области , то задача Коши

имеет единственное решение.

Условие Липшица является существенным для единственности решения задачи Коши. В качестве примера рассмотрим уравнение

Нетрудно видеть, что функция непрерывна; с другой стороны,

и условие Липшица не удовлетворяется ни в одной области, содержащей начало координат , так как множитель при оказывается неограниченным при .

Данное дифференциальное уравнение допускает решение где — произвольная постоянная. Отсюда видно, что существует бесконечное множество решений, удовлетворяющих начальному условию

Общим решением дифференциального уравнения (2) называется функция

зависящая от одной произвольной постоянной , и такая, что

1) она удовлетворяет уравнению (2) при любых допустимых значениях постоянной ;

2) каково бы ни было начальное условие

можно подобрать такое значение постоянной , что решение будет удовлетворять заданному начальному условию (4). При этом предполагается, что точка принадлежит области, где выполняются условия существования и единственности решения.

Частным решением дифференциального уравнения (2) называется решение, получаемое из общего решения (3) при каком-либо определенном значении произвольной постоянной .

Пример 1. Проверить, что функция есть общее решение дифференциального уравнения и найти частное решение, удовлетворяющее начальному условию . Дать геометрическое истолкование результата.

Решение. Функция удовлетворяет данному уравнению при любых значениях произвольной постоянной . В самом деле,

Зададим произвольное начальное условие . Полагая и в равенстве , найдем, что . Подставив это значение в данную функцию, будем иметь . Эта функция удовлетворяет заданному начальному условию: положив , получим . Итак, функция является общим решением данного уравнения.

В частности, полагая и , получим частное решение .

Общее решение данного уравнения, т.е. функция , определяет в плоскости семейство параллельных прямых с угловым коэффициентом . Через каждую точку плоскости проходит единственная интегральная линия . Частное решение определяет одну из интегральных кривых, а именно прямую, проходящую через начало координат (рис.4).

Пример 2. Проверить, что функция есть общее решение уравнения и найти частное решение, удовлетворяющее начальному условию .

Решение. Имеем . Подставляя в данное уравнение выражения и , получаем , т. е. функция удовлетворяет данному уравнению при любых значениях постоянной .

Зададим произвольное начальное условие . Подставив и вместо и в функцию , будем иметь , откуда . Функция удовлетворяет начальному условию. Действительно, полагая , получим . Функция есть общее решение данного уравнения.

При и получим частное решение .

С геометрической точки зрения общее решение определяет семейство интегральных кривых, которыми являются графики показательных функций; частное решение есть интегральная кривая, проходящая через точку (рис.5).

Соотношение вида , неявно определяющее общее решение, называется общим интегралом дифференциального уравнения первого порядка.

Соотношение, получаемое из общего интеграла при конкретном значении постоянной , называется частным интегралом дифференциального уравнения.

Задача решения или интегрирования дифференциального уравнения состоит в нахождении общего решения или общего интеграла данного дифференциального уравнения. Если дополнительно задано начальное условие, то требуется выделить частное решение или частный интеграл, удовлетворяющие поставленному начальному условию.

Так как с геометрической точки зрения координаты и равноправны, то наряду с уравнением мы будем рассматривать уравнение .

Условия равномерной экспоненциальной устойчивости дифференциальных уравнений

В статье рассматривается вопрос о существенности условия Липшица для равномерной экспоненциальной устойчивости дифференциальных уравнений с управлением. Приводятся возможные условия, компенсирующие нелипшицевость правой части уравнения.

Рассмотрим дифференциальное уравнение с малым параметром вида

(1)

В этом уравнении функция f:R₊×R n ×R m →R n , y:R₊→R m , y(⋅)∈Y, где Y – подмножество множества всех измеримых функций, μ – малый параметр, 0≤μ≤μ_*, μ_*>0.

Определим решение системы (1) с начальным условием x(t₀)=x₀∈R n как абсолютно непрерывную функцию x(t), удовлетворяющую системе (1) почти при всех t≥t₀ и для всех функций y(⋅)∈Y.

Положение равновесия 0∈R n системы (1) будем называть равномерно экспоненциально устойчивым, если существуют такие постоянные A>0, α>0, и μ₀>0, что для всех значений малого параметра возмущения μ ∈ (0, μ₀] любых начальных условий (t₀,x₀)∈R₊×R n , времени t≥t₀ и всех функций y(⋅)∈Y, соответствующие траектории (1) удовлетворяют оценке

Одновременно с задачей Коши для уравнения (1) рассмотрим усредненную задачу Коши, которая описывается неавтономным дифференциальным включением

(2)

В правой части отображение F:R₊×R n →Kv(R n ), где Kv(R n ) – класс непустых компактных выпуклых множеств из R n .

Нулевое решение задачи (2) будем называть равномерно экспоненциально устойчивым, если существуют постоянные A>0, β>0, и μ₁>0, такие что для всех значений параметра μ∈ (0,μ₁] для любых начальных условий (t₀,x₀) ∈ R₊×R n и любого решения ξ(t) задачи (2) справедливо неравенство

Условия, при которых равномерная экспоненциальная устойчивость усредненной системы наследуется возмущенной системой (1) при малых значениях параметра возмущения μ>0, рассматривались в работах [4, 1]. В частности, в статье [4] доказано, что при условии липшицевости правых частей возмущенной и усредненной систем, а также при некоторых дополнительных предположениях, из равномерной экспоненциальной устойчивости автономной усредненной задачи следует равномерная экспоненциальная устойчивость исходной задачи [4, теорема 3.1]. Авторы этой статьи считают условие Липшица существенным для доказанной теоремы.

Однако, в [1] доказано достаточное условие равномерной экспоненциальной устойчивости для более общего случая неавтономной системы сравнения, причем условие липшицевости правой части дифференциального включения (2) заменено на более слабое условие односторонней липшицевости [3], а от функции f в правой части исходной задачи (1) не требуется даже этого условия, но предполагается существование решения. Отсутствие липшицевости правых частей f и F из задач (1) и (2) компенсируется предположением линейного роста и условиями, обеспечивающими для отображения равномерную непрерывность по переменной z а для отображения – равномерную полунепрерывность сверху по фазовой переменной, равномерную по t на R₊. Для доказательства этой теоремы существенно используется критерий равномерной экспоненциальной устойчивости, доказанный в [2, теорема 1] для дифференциальных включений. Приведем этот критерий, сформулировав его для рассматриваемых нами задач (1) и (2).

Предположим, то существует неубывающая функция Γ:0,+∞)→R₊ такая, что для произвольных начальных данных (t0,x0)∈R₊×R n и любого решения задачи (1) справедлива оценка

(3)

Постоянная H>0 выбирается так, чтобы выполнялось неравенство

где B и β – постоянные из определения равномерной экспоненциальной устойчивости усредненной системы.

Основное условие критерия равномерной экспоненциальной устойчивости формулируется следующим образом:

(*) для некоторых постоянных H и p, удовлетворяющих неравенству (4), существуют постоянные q∈[0,1), μ2>0 такие, что p+q n и любого решения x(t) задачи (1) найдется такое решение усредненной задачи (2), для которого

Теорема 1 [2, критерий равномерной экспоненциальной устойчивости]. Пусть для любого решения задачи (1) имеет место неравенство (3), и усредненная система (2) является равномерно экспоненциально устойчивой. Тогда для равномерной экспоненциальной устойчивости дифференциального уравнения (1) необходимо и достаточно, чтобы выполнялось условие (*).

Рассмотрим теперь пример из [4], демонстрирующий, по мнению авторов статьи, существенность условия Липшица для правой части возмущенной системы, и покажем, что отсутствие равномерной экспоненциальной устойчивости исходного дифференциального уравнения связано не с отсутствием липшицевости, а с невыполнением априорных оценок в теореме 1.

Пример [4, пример 4.3]. Рассмотрим возмущенное дифференциальное уравнение

(5)

где для x>0 определим

При x≤0 и t≥0 определим f(t,x)=-f(t,-x), и f(t,0)=0 при всех t≥0.

Отображение f(t,x) непрерывно на [0,+∞)×R, но не липшицево по переменной x. Однако, кроме этого, для системы (5) не выполняется также априорная оценка решения (3), так как для любого фиксированного параметра возмущения μ>0 начальному значению x₀=0 соответствует траектория при t ∈ [0,1]. Очевидно, что начало 0∈R не является точкой равновесия экспоненциальной устойчивости для возмущенной системы.

В качестве системы сравнения рассмотрим дифференциальное уравнение

Усредненная система равномерно экспоненциально устойчива.

Таким образом, для достаточного условия равномерной экспоненциальной устойчивости дифференциальных уравнений с управлением существенным является выполнение априорной оценки (3). А эта оценка справедлива не только при условии липшицевости отображения f из задачи (1), но и при выполнении других условий, например, условия линейного роста, что и было использовано в работе [1].