Условие разрешимости задачи неймана для уравнения пуассона

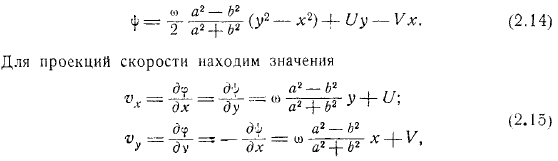
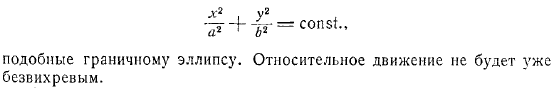
Граничные условия. Задачи Дирихле и Неймана

Поиск комплексного потенциала, определяющего планарное невращательное движение несжимаемой жидкости гидромеханики, можно свести к поиску функции потока, поскольку потенциал связан с известными условиями Коши. Римана, из известной функции можно определить в виде квадратуры. Функция потока, которая считается непрерывной во всех точках течения несжимаемой жидкости, удовлетворяет уравнению Лапласа в этих точках, а на определенных границах течения-некоторым известным условиям. Формат зависит от реализации квартиры.

Показаны простейшие случаи, без цели исчерпывающей классификации различных типов граничных условий. Рассматривая плоское течение бесконечно статичной бесконечной жидкости о движении тела в идеальной жидкости, возникающее при движении цилиндра, граничные условия для функции потока однозначно следующие — поскольку скорость в этих точках должна быть равна нулю. В каждой точке контура движущегося тела, нормальная проекция скорости должны совпадать.

Угол между элементом линии потока и осью, а соотношение между позволяет выразить рассматриваемое условие. И если в жидкости еще есть неподвижный объект, то по их контуру понятно, что обычная составляющая скорости соседних частиц жидкости должна быть равна нулю, другими словами, сам неподвижный контур должен находиться в контакте с текущей линией. В этом случае необходимо добавить граничное условие к предыдущему условию. Для точки фиксированного контура.

Если тело движется поступательно со скоростью, направленной вдоль оси, то условие равно. Принять форму, или все точки контура, после того как цилиндрический объект совершает какое-либо движение. При наличии поступательного потока с бесконечно большой скоростью расстояние до удаленной точки равно, ориентированной вдоль оси и обтекающей неподвижный объект. Граничное условие, очевидно, выглядит так: для бесконечности показанные нами граничные условия в основном используются при исследовании стационарного движения, но остаются справедливыми для нестационарного потенциала.

В этом случае предыдущее выражение вводит только время в качестве параметра. Параметры зависят от. Известное значение функции на контуре области называется задачей Дирихле, хотя это задача определения функции, удовлетворяющей уравнению Лапласа в области. Таким образом, мы видим, что определение плоского невращательного движения несжимаемой жидкости, вызванного движением контура, ограничивающего область течения, приводит к решению конкретной задачи Дирихле.

При решении гидродинамических задач можно также сначала найти все потенциалы скорости. Он также должен удовлетворять уравнению Лапласа в области течения. Но является ли граничное условие схемы необходимым для функции? Другой само определение потенциала скорости является вертикальной проекцией в скорости частицы жидкости, прилегающие к контуру, и, следовательно, граничное условие для функции принимает форму an является нормальной проекции скорости точки контура. В частности, в терминах фиксированных границ, мы получим условие.

Моделью идеальной жидкости пользуются при теоретическом рассмотрении задач, в которых вязкость не является определяющим фактором и ею можно пренебречь. Людмила Фирмаль

В области, задача определения функции, которая удовлетворяет уравнению Лапласа по известному значению нормальной производной функции на контур области называется задачей Неймана. Поэтому гидродинамические задачи приводят к решению некоторых задач Неймана. Вы можете использовать функцию для определения функции и наоборот. Поэтому ясно, что задача Неймана может быть сведена к задаче Дирихле, или наоборот. Факт, запомните состояние Коши-Римана и проследите за цифрой некоторое время.

Направление нормали в направлении оси, и направление касательной в направлении оси, получаем следующие соотношения сразу, вы можете перейти к задаче Неймана из задачи Дирихле, если есть проблема Неймана, то есть, если вы знаете значение на схеме, это будет следующим образом. Переходим к границе области течения, и поэтому Дирихле. В случае задачи многосвязной области с границей на контуре предыдущее выражение отображает значение аддитивной постоянной для каждой схемы. По значению одной из этих аддитивных констант движение определяется значением производной функции, поэтому его можно выбрать.

Любые константы в будут отображаться. Дана циркуляция скоростей по контуру, которые неприводимы друг к другу. Это полностью совпадает с замечанием о том, что вращательные движения, сделанные в конце раздела главы движение кругового цилиндра , полностью определяются задачей. И цикл только в том случае, если настройка циклическая. В качестве простого примера рассмотрим задачу о невращательном движении несжимаемой жидкости, заключенной в эллиптический цилиндр. Пусть эллиптическое уравнение.

Его движение характеризуется проекцией на координатную ось скорости и угла поворота скорости его центра. Тогда функция потока должна удовлетворять уравнению в эллипсе и граничному условию самого эллипса. Полином порядка. Я ищу функцию в виде. Уравнение представляет собой отношение. Уравнение из условия является результатом. Это означает связь между для проекции скорости найдите значение, вы можете получить оттуда легко.

Простейший случай чистого поступательного движения цилиндра, когда, выглядит так: то есть жидкость движется вместе со всем цилиндром. Для чистого вращения, когда, это выглядит так: линия потока абсолютного движения гиперболическая. Подчеркнем, что полученная нами формула определяет абсолютное движение жидкости, но относится к движущимся координатным осям.

Движение жидкости относительно этих движущихся координатных осей определяется вычитанием проекции переносной скорости из проекции абсолютной скорости. В результате проекция относительной скорости выглядит следующим образом и представляет собой эллипс, аналогичный граничному эллипсу. Относительное движение больше не является вихревым.

В частности, такая идеализация допустима во многих случаях течения, рассматриваемых гидроаэромеханикой, и даёт хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твёрдых поверхностей и поверхностей раздела с неподвижной средой. Людмила Фирмаль

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

неймана задача

НЕЙМАНА ЗАДАЧА — задача о нахождении решения Лапласа уравнения Du = 0 или Пуассона уравнения Du = —f в области G (внутр. H. з.) или вне её (внеш. H. з.), имеющего на границе S области G заданную непрерывную нормальную производную u 1 (соответственно внутри и извне S). При постановке внеш. H. з. требуется, чтобы решение на бесконечности стремилось к нулю в трёхмерном и было ограниченным в двумерном случаях.

H. з. для ур-ний Пуассона и Лапласа связаны подстановкой u(x)= и(х) — V(x), где в трехмерном случае

— объёмный потенциал, а в двумерном — логариф-мич. потенциал; очевидным образом связаны и граничные значения u 1 и u 1 . Внеш. H. з. связана с внутренней преобразованием Кельвина, т. е. переходом к новым координатам x x‘ = xR 2 /x 2 и новой ф-ции

(в двумерном случае множитель R/|x‘| перед и отсутствует). Координаты x и х‘ симметричны относительно сферы радиуса R с центром в начале координат.

Решение внутр. H. з. существует, единственно с точностью до постоянной и непрерывно зависит от граничных условий для достаточно гладких границ S (в частности, для S, задаваемых в окрестности каждой своей точки x 0 ур-нием f x о = 0 с условием, что О, a f x о непрерывна вместе со своими производными). Необходимым условием разрешимости внутр. H. з. (а также внеш. H. з. в двумерном случае) является равенство

Решение H. з. для ур-ния Лапласа обычно представляется в виде потенциала простого слоя

(в двумерном случае вместо |х — у| -1 стоит -ln |х — у|)и сводится к решению Фредгольма уравнения для плотности m(x):

где «+» соответствует внутренней»-» внешней Н.э., y xy — угол между вектором x — у и нормалью к S в точке у, dS y — элемент поверхности в точке у.

H. з. часто встречается в электро- и магнитостатике, стационарных задачах гидродинамики, теплопроводности и т. д. Условие её разрешимости имеет физ. смысл закона сохранения: суммарный поток (напряжённости электрич. или магн. поля, несжимаемой жидкости, тепла и т. д.) через замкнутую поверхность S равен суммарной величине источников (заряда и т. п.).

Лит.: Владимиров В. С., Уравнения математической физики, 5 изд., M., 1988; Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., M., 1957; Tихонов A. H., Самарский А. А., Уравнения математической физики, 5 изд., M., 1977. В. П. Павлов.

Уравнения математической физики (стр. 2 )

Из за большого объема этот материал размещен на нескольких страницах:
1 2 3 4

Подраздел 5. Некоторые сведения из теории линейных функционалов и операторов в гильбертовых пространствах.

Формальное построение интеграла Фурье. Представление функции в виде интеграла Фурье. Условие Дини. Преобразование Фурье и его свойства. Преобразование Фурье быстро убывающих функций. Преобразование Фурье свертки. Теорема Планшереля.

Определение гильбертова пространства и унитарного оператора. Теорема о существовании счетного ортонормированного базиса в сепарабельном гильбертовом пространстве. Теорема Рисса. Определение ограниченного оператора, компактного оператора. Норма оператора. Спектр оператора (точечный, непрерывный, остаточный). Теорема о спектре компактного оператора. Теорема Фредгольма. Теорема Гильберта–Шмидта.

Раздел 2. Эллиптические задачи.

Подраздел 1. Разрешимость задачи Дирихле и задачи Неймана для уравнения Пуассона.

Постановка задачи Дирихле для уравнения Пуассона. Определение классического решения. Определение обобщенного решения. Существование и единственность обобщенного решения задачи Дирихле для уравнения Пуассона.

Собственные значения и собственные функции эллиптических задач. Нахождение решения задачи Дирихле для уравнения Пуассона с помощью разложения в ряд по собственным функциям.

Формула интегрирования по частям.

Фредгольмова разрешимость задачи Дирихле для уравнения Пуассона.

Проблема минимума квадратичного функционала. Существование и единственность минимизирующего элемента для квадратичного функционала. Метод Ритца. Вариационный метод решения задачи Дирихле для уравнения Пуассона.

Разрешимость задачи Неймана для уравнения Пуассона. Обобщенные и классические решения. Необходимое и достаточное условие существования обобщенного решения. Собственные значения и собственные функции оператора Лапласа с условиями Неймана.

Подраздел 2. Обобщенные и классические решения эллиптических задач, гладкость решений.

Гладкость обобщенных решений эллиптических задач внутри области. Обобщение результатов на случай . Гладкость обобщенных решений эллиптических задач вблизи границы. Обобщение результатов на случай .

Теоремы о гладкости обобщенного решения задачи Дирихле для уравнения Пуассона (локально и в замыкании области). Связь между обобщенными и классическими решениями. Гладкость обобщенных собственных функций задачи Дирихле для уравнения Пуассона.

Гладкость обобщенных решений задачи Неймана для уравнения Пуассона (внутри области и вблизи границы). Следствия.

Формула Грина. Интегральное представление функций. Первая теорема о среднем. Вторая теорема о среднем. Принцип максимума. Единственность классического решения задачи Дирихле для уравнения Пуассона

Раздел 3. Эволюционные уравнения.

Формальное решение смешанных задач для волнового уравнения методом Фурье. Существование и единственность обобщенного решения первой смешанной задачи для волнового уравнения. Представимость решения в виде ряда. Априорная оценка решения.

Формальное решение смешанных задач для уравнения теплопроводности методом Фурье. Существование и единственность обобщенного решения первой смешанной задачи для уравнения теплопроводности.

Приближенное решение смешанных задач для волнового уравнения и уравнения теплопроводности методом Галеркина.

Формула Кирхгофа. Формулы Пуассона и Даламбера. Метод спуска.

Существование и единственность классического решения задачи Коши для волнового уравнения.

Решение задачи Коши для уравнения теплопроводности.

Раздел 4. Теория полугрупп и ее приложения.

Примеры задач, порождающих полугруппы. Равномерно непрерывные полугруппы. Генератор полугруппы. Теоремы о генераторе полугруппы.

Определение сильно непрерывной полугруппы. Оценка на рост полугруппы. Теоремы о генераторе сильно непрерывной полугруппы.

Теорема Хилле-Иосиды. Следствия из теоремы Хилле-Иосиды.

Решение задачи Коши для операторно-дифференциальных уравнений методом полугрупп. Решение смешанных задач для параболических дифференциальных уравнений методом полугрупп. Решение задачи Коши для уравнения диффузии методом полугрупп.

Конкретный перечень знаний, умений и навыков по каждой теме и требования к минимальному уровню их освоения (в соответствии с приказом ректора № 000 от 20 июня 2013 г.)

Перечень знаний, умений и навыков по теме

Требования к минимальному уровню освоения

Введение в уравнения с частными производными, постановка задач математической физики

основные определения и обозначения, используемые в курсе уравнений математической физики;

классификацию линейных уравнений в частных производных второго порядка. Уметь:

приводить примеры уравнений в частных производных различных классов;

записывать матрицу перехода и трансформацию уравнения при замене системы координат;

формулировать задачу Коши для волнового уравнения и для уравнения теплопроводности;

формулировать смешанные задачи для волнового уравнения и для уравнения теплопроводности;

формулировать краевые задачи для уравнения Пуассона;

приводить к каноническому виду линейные уравнения в частных производных второго порядка;

находить общее решение линейного уравнения в частных производных второго порядка.

основные определения и обозначения, используемые в курсе уравнений математической физики;

классификацию линейных уравнений в частных производных второго порядка.

определять тип уравнения в частных производных;

формулировать задачу Коши для волнового уравнения и для уравнения теплопроводности;

формулировать смешанные задачи для волнового уравнения и для уравнения теплопроводности;

формулировать краевые задачи для уравнения Пуассона;

приводить к каноническому виду линейное уравнение в частных производных второго порядка с переменными коэффициентами в плоской области;

приводить к каноническому виду линейное уравнение в частных производных второго порядка с постоянными коэффициентами в пространстве;

находить общее решение линейного уравнения в частных производных второго порядка.

Пространство интегрируемых функций

определение ядра усреднения;

определение срезающей функции;

формулировку теоремы о разбиении единицы;

определение пространства интегрируемых функций;

формулировку теоремы о непрерывности интегрируемых функций в среднеквадратичном;

формулировку теоремы об усреднении интегрируемой функции;

свойства пространства интегрируемых функций.

строить примеры срезающих функций;

доказывать теоремы о разбиении единицы, о непрерывности интегрируемых функций в среднеквадратичном, об усреднении интегрируемой функции;

доказывать свойства пространства интегрируемых функций.

формулировку теоремы о разбиении единицы;

определение пространства интегрируемых функций;

формулировку теоремы о непрерывности интегрируемых функций в среднеквадратичном;

формулировку теоремы об усреднении интегрируемой функции;

строить примеры срезающих функций;

доказывать свойства пространства интегрируемых функций (гильбертовость, сепарабельность, всюду плотность пространства бесконечно дифференцируемых функций с компактным носителем в пространстве интегрируемых функций).

Обобщенные производные и конечные разности

определение обобщенной производной;

формулировку теоремы о единственности обобщенной производной;

формулировку теоремы о независимости обобщенной производной от порядка дифференцирования;

свойства обобщенных производных;

необходимое и достаточное условие равенства функции константе почти всюду в ограниченной области;

определение конечно-разностных отношений.

доказывать теоремы о единственности обобщенной производной, о независимости обобщенной производной от порядка дифференцирования;

производить усреднение обобщенных производных;

аппроксимировать обобщенные производные финитных функций конечноразностными отношениями;

аппроксимировать обобщенные производные функций с носителем вблизи границы конечноразностными отношениями.

определение обобщенной производной;

формулировку теоремы о единственности обобщенной производной;

формулировку теоремы о независимости обобщенной производной от порядка дифференцирования;

свойства обобщенных производных;

необходимое и достаточное условие равенства функции константе почти всюду в ограниченной области;

вычислять обобщенную производную для функций , и других;

аппроксимировать обобщенные производные финитных функций конечноразностными отношениями;

определение пространства Соболева ; формулы скалярного произведения и нормы в ;

формулировку теоремы о полноте;

свойства пространств Соболева;

формулировки теорем о продолжении функций (в кубе, в ограниченной области с гладкой границей);

формулировку теоремы о всюду плотности пространства бесконечно дифференцируемых функций в пространстве Соболева;

определение следа функции;

определение пространства ;

формулировку теоремы об эквивалентном определении пространства (характеристическое свойство);

формулировку теоремы об эквивалентном скалярном произведении в ;

определение непрерывности вложения; формулу эквивалентной нормы в пространстве Соболева, определяемой через преобразование Фурье;

формулировку теоремы вложения Соболева;

определение и свойства анизотропных пространств Соболева.

доказывать теорему о полноте;

доказывать свойства пространств Соболева;

доказывать теоремы о продолжении функций (в кубе, в ограниченной области с гладкой границей);

доказывать теорему о всюду плотности пространства бесконечно дифференцируемых функций в пространстве Соболева;

доказывать сепарабельность пространства Соболева в случае ограниченной области с гладкой границей;

доказывать компактность оператора вложения пространства Соболева в пространство интегрируемых функций;

доказывать теорему об эквивалентном определении пространства (характеристическое свойство);

доказывать теорему об эквивалентном скалярном произведении в ;

доказывать теорему вложения Соболева;

доказывать свойства анизотропных пространств Соболева.

определение пространства Соболева ; формулы скалярного произведения и нормы в ;

свойства пространств Соболева;

формулировки теорем о продолжении функций;

определение пространства ;

характеристическое свойство пространства );

формулу эквивалентного скалярного произведения в ;

формулу эквивалентной нормы в пространстве Соболева, определяемой через преобразование Фурье;

формулировку теоремы вложения Соболева;

определение и свойства анизотропных пространств Соболева.

доказывать свойства пространств Соболева;

доказывать компактность оператора вложения пространства Соболева в пространство интегрируемых функций;

доказывать теорему об эквивалентном скалярном произведении в ;

доказывать свойства анизотропных пространств Соболева;

исследовать функцию на принадлежность пространству Соболева

Некоторые сведения из теории линейных функционалов и операторов в гильбертовых пространствах

формальное построение интеграла Фурье;

определение преобразования Фурье и его свойства;

преобразование Фурье быстро убывающих функций и преобразование Фурье свертки; формулировку теоремы Планшереля;

теорему о существовании счетного ортонормированного базиса в сепарабельном гильбертовом пространстве;

определение спектра оператора (точечного, непрерывного, остаточного).

представлять заданную функцию в виде интеграла Фурье;

выводить формулу преобразования Фурье;

вычислять преобразование Фурье заданной функции;

формулировать теоремы Рисса, Фредгольма, Гильберта–Шмидта и теорему о спектре компактного оператора.

формальное построение интеграла Фурье;

определение преобразования Фурье и его свойства;

формулировку теорем Рисса, Фредгольма и Гильберта–Шмидта.

записывать условие Дини;

представлять заданную функцию в виде интеграла Фурье;

выводить формулу преобразования Фурье;

вычислять преобразование Фурье заданной функции.

Разрешимость задачи Дирихле и задачи Неймана для уравнения Пуассона

постановку задачи Дирихле для уравнения Пуассона;

определение классического решения задачи Дирихле для уравнения Пуассона;

определение обобщенного решения задачи Дирихле для уравнения Пуассона;

условия существования и единственности обобщенного решения задачи Дирихле для уравнения Пуассона;

алгоритм нахождения решения задачи Дирихле для уравнения Пуассона с помощью разложения в ряд по собственным функциям;

формулу интегрирования по частям;

условия Фредгольмовой разрешимости задачи Дирихле для уравнения Пуассона;

постановку проблемы минимума квадратичного функционала;

вариационный метод решения задачи Дирихле для уравнения Пуассона;

постановку задачи Неймана для уравнения Пуассона;

определение обобщенного и классического решения задачи Неймана для уравнения Пуассона.

решать задачу Дирихле для уравнения Пуассона;

формулировать и доказывать теоремы о существовании и единственности обобщенного решения задачи Дирихле для уравнения Пуассона;

оперировать с собственными значениями и собственными функциями эллиптических задач;

находить решения задачи Дирихле для уравнения Пуассона с помощью разложения в ряд по собственным функциям;

доказывать формулу интегрирования по частям;

доказывать существование и единственность минимизирующего элемента для квадратичного функционала;

доказывать необходимое и достаточное условие существования обобщенного решения задачи Неймана для уравнения Пуассона;

находить собственные значения и собственные функции оператора Лапласа с условиями Неймана.

постановку задачи Дирихле для уравнения Пуассона;

определение классического решения задачи Дирихле для уравнения Пуассона;

определение обобщенного решения задачи Дирихле для уравнения Пуассона;

формулу интегрирования по частям;

вариационный метод решения задачи Дирихле для уравнения Пуассона;

постановку задачи Неймана для уравнения Пуассона;

определение обобщенного и классического решения задачи Неймана для уравнения Пуассона.

решать задачу Дирихле для уравнения Пуассона;

формулировать теоремы о существовании и единственности обобщенного решения задачи Дирихле для уравнения Пуассона;

оперировать с собственными значениями и собственными функциями эллиптических задач;

находить решения задачи Дирихле для уравнения Пуассона с помощью разложения в ряд по собственным функциям;

доказывать формулу интегрирования по частям;

формулировать необходимое и достаточное условие существования обобщенного решения задачи Неймана для уравнения Пуассона;

находить собственные значения и собственные функции оператора Лапласа с условиями Неймана;

решать краевую задачу для уравнения Пуассона в прямоугольнике;

решать краевую задачу для уравнения Пуассона в круге (секторе).

Обобщенные и классические решения эллиптических задач, гладкость решений.

формулировки теорем о гладкости обобщенных решений эллиптических задач внутри области;

формулировки теорем о гладкости обобщенных решений эллиптических задач вблизи границы;

формулировки теорем о гладкости обобщенного решения задачи Дирихле для уравнения Пуассона (локально и в замыкании области);

связь между обобщенными и классическими решениями задачи Дирихле для уравнения Пуассона;

формулировки теорем об интегральном представлении функций;

формулировки первой и второй теорем о среднем;

формулировку принципа максимума.

доказывать теоремы о гладкости обобщенных решений эллиптических задач внутри области;

обобщать результаты на случай ;

доказывать теоремы о гладкости обобщенных решений эллиптических задач вблизи границы;

обобщать результаты на случай ;

доказывать теоремы о гладкости обобщенного решения задачи Дирихле для уравнения Пуассона (локально и в замыкании области);

доказывать утверждения о гладкости обобщенных собственных функций задачи Дирихле для уравнения Пуассона;

доказывать утверждения о гладкости обобщенных решений задачи Неймана для уравнения Пуассона (внутри области и вблизи границы) и следствия из этих результатов;

выводить формулу Грина;

доказывать результат об интегральном представлении функций;

доказывать первую и вторую теоремы о среднем;

доказывать принцип максимума;

доказывать единственность классического решения задачи Дирихле для уравнения Пуассона.

формулировки теорем о гладкости обобщенных решений эллиптических задач внутри области и вблизи границы;

формулировки теорем об интегральном представлении функций;

формулировки первой и второй теорем о среднем;

формулировку принципа максимума.

выводить формулу Грина;

доказывать результат об интегральном представлении функций;

доказывать первую и вторую теоремы о среднем;

доказывать единственность классического решения задачи Дирихле для уравнения Пуассона.

решать краевую задачу для оператора Лапласа при помощи функции Грина.

алгоритм формального решения смешанных задач для волнового уравнения методом Фурье;

формулировки теорем о существовании и единственности обобщенного решения первой смешанной задачи для волнового уравнения;

представление решения смешанной задачи для волнового уравнения в виде ряда; априорную оценку решения;

алгоритм формального решения смешанных задач для уравнения теплопроводности методом Фурье;

формулировки теорем о существовании и единственности обобщенного решения первой смешанной задачи для уравнения теплопроводности;

формулы Кирхгофа, Пуассона и Даламбера; метод спуска;

формулировку теоремы о существовании и единственности классического решения задачи Коши для волнового уравнения;

алгоритм решения задачи Коши для уравнения теплопроводности.

строить формальное решение смешанных задач для волнового уравнения методом Фурье;

представлять решение в виде ряда;

доказывать существование и единственность обобщенного решения первой смешанной задачи для волнового уравнения;

доказывать априорную оценку решения;

строить формальное решение смешанных задач для уравнения теплопроводности методом Фурье;

доказывать существование и единственность обобщенного решения первой смешанной задачи для уравнения теплопроводности;

решать смешанные задачи для волнового уравнения и уравнения теплопроводности методом Галеркина;

доказывать формулу Кирхгофа;

доказывать формулы Пуассона и Даламбера методом спуска;

доказывать существование и единственность классического решения задачи Коши для волнового уравнения;

решать задачу Коши для уравнения теплопроводности.

алгоритм формального решения смешанных задач для волнового уравнения методом Фурье;

представление решения смешанной задачи для волнового уравнения в виде ряда;

априорную оценку решения;

алгоритм формального решения смешанных задач для уравнения теплопроводности методом Фурье;

формулы Кирхгофа, Пуассона и Даламбера; формулировку теоремы о существовании и единственности классического решения задачи Коши для волнового уравнения;

алгоритм решения задачи Коши для уравнения теплопроводности.

решать смешанную задачу для гиперболического уравнения;

решать смешанную задачу для параболического уравнения;

решать смешанные задачи для волнового уравнения и уравнения теплопроводности методом Галеркина;

формулировать основную идею метода спуска;

решать задачу Коши для волнового уравнения;

решать задачу Коши для уравнения теплопроводности;

исследовать область зависимости решения волнового уравнения от начальных данных и правой части уравнения.

Теория полугрупп и ее приложения

примеры задач, порождающих полугруппы;

определения равномерно непрерывной полугруппы, генератора полугруппы;

формулировки теорем о генераторе полугруппы;

определение сильно непрерывной полугруппы;

оценку на рост полугруппы;

формулировки теорем о генераторе сильно непрерывной полугруппы;

определение сжимающего оператора;

определение резольвенты и резольвентного множества;

формулировку теоремы Хилле-Иосиды;

следствия из теоремы Хилле-Иосиды;

способ решения задачи Коши для операторно-дифференциальных уравнений методом полугрупп;

способ решения смешанных задач для параболических дифференциальных уравнений методом полугрупп;

способ решения задачи Коши для уравнения диффузии методом полугрупп.

строить примеры задач, порождающих полугруппы;

доказывать теоремы о генераторе полугруппы;

определять, является ли оператор генератором полугруппы;

доказывать оценку на рост полугруппы;

доказывать теоремы о генераторе сильно непрерывной полугруппы;

определять, является ли оператор генератором сильно непрерывной полугруппы;

доказывать теорему Хилле-Иосиды и следствия из нее;

формулировать и доказывать теоремы о решение задачи Коши для операторно-дифференциальных уравнений методом полугрупп;

формулировать и доказывать теоремы о решении смешанных задач для параболических дифференциальных уравнений методом полугрупп;

формулировать и доказывать теоремы о решении задачи Коши для уравнения диффузии методом полугрупп.

примеры задач, порождающих полугруппы;

определения равномерно непрерывной полугруппы, генератора полугруппы;

формулировки теорем о генераторе полугруппы;

определение сильно непрерывной полугруппы;

определение сжимающего оператора;

определение резольвенты и резольвентного множества;

формулировку теоремы Хилле-Иосиды;

строить примеры задач, порождающих полугруппы;

определять, является ли оператор генератором полугруппы;

определять, является ли оператор генератором сильно непрерывной полугруппы;

вычислять матричную экспоненту;

решать начально-краевую задачу для волнового уравнения на полуоси.

Описание количественных оценок с указанием соответствия баллов достигнутому уровню знаний, навыков и умений студента по каждому изучаемому разделу (теме) (в соответствии с приказом ректора № 000 от 01.01.01 г.)

источники:

http://www.femto.com.ua/articles/part_2/2424.html

http://pandia.ru/text/80/281/57249-2.php