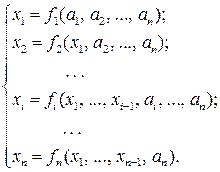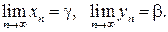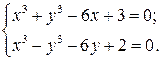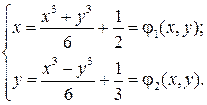Метод итераций
Правила ввода функции
- Примеры
≡ x^2/(1+x)
cos 2 (2x+π) ≡ (cos(2*x+pi))^2≡ x+(x-1)^(2/3)
На рис.1а, 1б в окрестности корня |φ′(x)| 1, то процесс итерации может быть расходящимся (см. рис.2).
Достаточные условия сходимости метода итерации
Процесс нахождения нулей функции методом итераций состоит из следующих этапов:
- Получить шаблон с омощью этого сервиса.
- Уточнить интервалы в ячейках B2 , B3 .
- Копировать строки итераций до требуемой точности (столбец D ).
Примечание: столбец A — номер итерации, столбец B — корень уравнения X , столбец C — значение функции F(X) , столбец D — точность eps .
Условия сходимости метода простой итерации для нелинейных систем уравнений второго порядка
Дата добавления: 2013-12-23 ; просмотров: 4275 ; Нарушение авторских прав
Метод простой итерации
Постановка задачи
РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Многие практические задачи сводятся к решению систем нелинейных уравнений с n неизвестными:
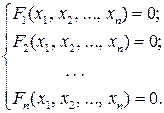
В отличие от линейных систем прямых методов решения систем нелинейных уравнений нет, за исключением систем второго порядка, когда одно неизвестное может быть выражено через другое.
Наиболее распространены два метода: метод простой итерации и метод Ньютона.
Система (4.1) должна быть представлена в следующем виде:
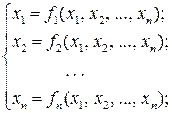
где 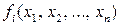
Алгоритм решения аналогичен алгоритму Зейделя или алгоритму простой итерации для решения систем линейных уравнений.
Пусть известен начальный вектор решения xi = ai, i = 1, 2, …, n, тогда
Итерационный процесс продолжается до тех пор, пока изменение всех неизвестных в двух последовательных итерациях не станет меньше заданного значения e.
Начальные значения должны быть близкими к истинным значениям, иначе итерационный процесс может не сойтись. Поэтому стоит проблема их отыскания (т. е. условий сходимости). В случае расходимости (несходимости) в блок-схеме алгоритма срабатывает механизм ограничения числа итераций.
Рассмотрим систему из двух уравнений общего вида:
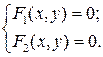
Нужно найти действительные корни x и y с заданной степенью точности e.
Предположим, что данная система имеет корни и их можно установить. Итак, для применения метода простой итерации систему (4.3) нужно привести к виду

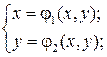
где j1 и j2 – итерирующие функции. По ним и строится итерационный процесс решения в виде
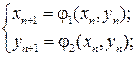
где при n = 0 x0 и y0 – начальные приближения.
Имеет место следующее утверждение: пусть в некоторой замкнутой области R(a £ x £ A; b £ y £ B) имеется одно и только одно единственное решение: x = g; y = b, тогда:
1) если j1(x, y) и j2(x, y) определены и непрерывно дифференцируемы в области R;
2) если начальное решение x0, y0 и все последующие решения xn, yn также принадлежат области R;
3) если в R выполняются неравенства
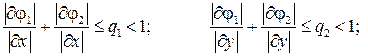
или равносильные неравенства

то итерационный процесс (4.5) сходится к определенным решениям, т. е.
Оценка погрешности n-го приближения дается неравенством

где М – наибольшее из чисел q1 или q2 в соотношениях (4.6) и (4.6а). Сходимость считается хорошей, если М –3 .
Пример 4.1. С заданной точностью решить нелинейную систему второго порядка:
Запишем систему в виде (4.4):
Рассмотрим квадрат 0 £ x £ 1; 0 £ y £ 1. Если взять х0 и у0 из этого квадрата, тогда
Из анализа вида j1 и j2 определим область нахождения их компонент при х = у = 1 в заданном квадрате.
Для j1(х, у): 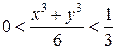
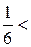
| | | следующая лекция ==> | |
| Общий алгоритм численных методов решения нелинейных уравнений | | | Метод Ньютона для системы двух уравнений |
Не нашли то, что искали? Google вам в помощь!
Условия сходимости итерационного метода нелинейные уравнения
Nickolay.info. Обучение. Лекции по численным методам. Приближённое решение нелинейных алгебраических уравнений
1. Приближенное решение нелинейных алгебраических уравнений
Дано нелинейное алгебраическое уравнение
Нелинейность уравнения означает, что график функции не есть прямая линия, т.е. в f(x) входит x в некоторой степени или под знаком функции.
Решить уравнение – это найти такое x* ∈ R: f(x*)=0. Значение x* называют корнем уравнения. Нелинейное уравнение может иметь несколько корней. Геометрическая интерпретация корней уравнения представлена на рис. 1. Корнями уравнения (1) являются точки x1*, x2*, x3*, в которых функция f(x) пересекает ось x.

В приближенных методах процесс нахождения решения, вообще говоря, бесконечен. Решение получается в виде бесконечной последовательности <xn>, такой, что 
Если корней несколько, то для каждого нужно найти интервал изоляции.
Существуют различные способы исследования функции: аналитический, табличный, графический.
Аналитический способ состоит в нахождении экстремумов функции f(x), исследование ее поведения при 
Графический способ – это построение графика функции f(x) и определение числа корней по количеству пересечений графика с осью x.
Табличный способ – это построение таблицы, состоящей из столбца аргумента x и столбца значений функции f(x). О наличии корней свидетельствуют перемены знака функции. Чтобы не произошла потеря корней, шаг изменения аргумента должен быть достаточно мелким, а интервал изменения достаточно широким.
Решить уравнение x 3 ‑ 6x 2 +3x+11=0, т.е. f(x)= x 3 ‑ 6x 2 +3x+11.
Найдем производную f / (x)=3x 2 -12x+3.
Найдем нули производной f / (x)=3x 2 -12x+3=0; D=144-4*3*3=108;
X1=
X2=
Так как f / (









Найдем интервалы изоляции для каждого из корней.
Рассмотрим для первого корня отрезок [-2, -1]:
f(-2)= -27 0, f / (x)>0 при 
Рассмотрим для второго корня отрезок [1, 3]:
f(1)= 9>0, f(3)= -7 / (x) 0, f / (x)>0 при 
http://life-prog.ru/1_16065_usloviya-shodimosti-metoda-prostoy-iteratsii-dlya-nelineynih-sistem-uravneniy-vtorogo-poryadka.html
http://nickolay.info/study/methods/01.html
 ≡ x^2/(1+x)
≡ x^2/(1+x)