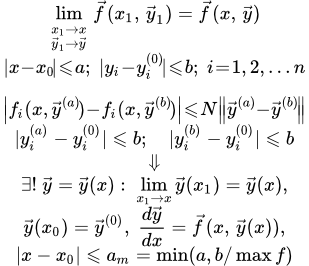Условия существования и единственности решения системы уравнений

Теорема существования и единственности решения системы дифференциальных уравнений

Здесь мы рассматриваем теорему существования и единственности решения системы дифференциальных уравнений с неизвестными функциями от переменной :
(1.1) ;
(1.2) ;
.
(1.n) .

Формулировка и доказательство этой теоремы является непосредственным обобщением теоремы для уравнения первого порядка, которое рассмотрено на странице “Теорема существования и единственности решения ДУ первого порядка”.

Векторная форма записи

Поскольку уравнения (1.1) – (1.n) однотипны, то мы применим векторную форму записи. Это позволит сократить объем выкладок и сделает доказательство более ясным.

Совокупность неизвестных функций мы будем обозначать одним вектором . Совокупность функций от независимой переменной и от зависимых функций мы обозначим как
.

То есть совокупность из величин мы будем обозначать вектором . Равенство

будет обозначать систему из уравнений:
,
где .

Под нормой вектора мы будем понимать сумму модулей его компонент:
.

Формулировка теоремы

Пусть дана система дифференциальных уравнений:
(1)
с начальными условиями
(1.0) .
Пусть – непрерывных функций от переменных в замкнутой области :

и, следовательно, ограничены некоторым положительным значением :
(2) .
И пусть функции удовлетворяют в области условию Липшица:
(3) ,
где – положительное число.
Тогда существует единственное решение системы (1):
,
удовлетворяющее начальным условиям , определенное и непрерывное для значений в интервале:
,
где есть наименьшее из двух чисел и .

Условие Липшица

Условие Липшица имеет вид:
(3) .
или в развернутом виде:
(3.1) ,
где – положительное число;
, и – любые значения из области .

Если условие Липшица выполняется и в некоторой точке существует частная производная , то она ограничена по модулю значением .
Для доказательства положим в (3.1) для всех . Тогда (3.1) примет вид:
.
Перейдем к пределу :
.

Если в области функции имеют непрерывные частные производные , то в этой области выполняется условие Липшица (3).
Для доказательства заметим, что поскольку частные производные непрерывны в замкнутой области, то они ограничены:
.
По теореме Лагранжа о конечных приращениях, имеем:
,
где частные производные вычисляются в некоторой точке , в которой компоненты принадлежат интервалам между и :
.
Тогда:

.

Доказательство существования решения

Приведем исходную систему (1) с начальными условиями (1.0) к системе интегральных уравнений. Левая и правая части (1) являются функциями от . Заменим на :
.
Интегрируем каждое уравнение по от до :
;
Подставим начальные условия . В результате получим систему интегральных уравнений:
(4) .

Покажем, что система интегральных уравнений (4) эквивалентна дифференциальным уравнениям (1) с начальными условиями (1.0). Для этого нужно показать, что из (1) и (1.0) следует (4) и из (4) следует (1) и (1.0). То, что из (1) и (1.0) следует (4) мы уже показали. Осталось показать, что из (4) следует (1) и (1.0). Для этого подставим в (4) . Получим начальные условия (1.0). Продифференцировав обе части системы (4) по , получаем (1).

Далее мы пытаемся найти решение уравнений (4) с помощью последовательных приближений. Для этого определяем ряд векторов функций от переменной по формулам:
(5.1) ;
(5.2) ;
(5.3) ;
.
(5.m) .
Функции непрерывны, потому что интеграл есть непрерывная функция от верхнего предела. Мы предполагаем, что при , стремится к решению системы (4):
(6) ,
где – решение системы (4). Если мы докажем это, то мы докажем существование решения.

Доказательство существования решения будем проводить в два этапа:
1> вначале докажем, что предел (6) существует;
2) затем докажем, что удовлетворяет системе (4):
.

1) Доказательство существования предела y (m) при m стремящемся к бесконечности

Сведем последовательные приближения (5.1) – (5.m) к суммам рядов. Для этого пишем:

.
Таким образом нам нужно доказать, что ряды
(7)
сходятся при .

Сначала покажем, что при , компоненты последовательных приближений принадлежат интервалу .
Действительно, при имеем:
.
Поскольку есть наименьшее из двух чисел и , то и
.

Далее, поскольку принадлежит интервалу , то . Тогда, аналогично предыдущему,
.
Отсюда
.

Далее, по индукции, поскольку принадлежит интервалу , то и
.
Отсюда
.

Итак, мы доказали, что последовательные приближения принадлежат интервалу
.
Теперь мы можем оценить члены ряда (7).

Для первого члена имеем:
;
(8.1) .
Для второго члена применяем условие Липшица и оценку (8.1):

;
(8.2) .

Далее применим метод индукции. Пусть
(8.m) .
Тогда

;
(8.m+1) .
Итак, поскольку (8.m) справедливо для и из (8.m) следует (8.m+1), то (8.m) выполняется для любых .

Запишем -й ряд (7) в виде:
(7.i) ,
где .
Применим (8.m) и заменим наибольшим допустимым значением :
.
Тогда каждый член ряда (7.i), кроме первого, ограничен по модулю членом ряда
(9) .
Исследуем ряд (9) на сходимость. Применим признак Даламбера:
.
Итак, ряд (9) сходится. Поскольку все члены ряда (7.i), начиная со второго, по абсолютной величине меньше членов сходящегося ряда (9), то, в силу критерия Вейерштрасса, ряд (7.i) сходится равномерно для всех , удовлетворяющих условию . Поскольку интеграл есть непрерывная функция от верхнего предела, то каждый член ряда (7.i) есть непрерывная функция от . Поэтому предел
(10)
существует и является непрерывной функцией от .

2) Доказательство того, что Y является решением (4)

Рассмотрим уравнение (5.m):
(5.m) .
Докажем, что при , это уравнение стремится к уравнению
(11) .

В силу (10) левая часть уравнения (5.m) стремится к .

Теперь покажем, что
.

Перепишем правую часть (5.m):
.
Далее заметим, что поскольку все принадлежат закрытому интервалу , то и принадлежит этому интервалу, . Поэтому мы можем применить условие Липшица.

Оценим абсолютную величину последнего члена:

.
Поскольку, при , стремится к равномерно, то для любого положительного числа можно указать такое натуральное число , что для всех ,
(12) .
Пусть есть наибольшее из чисел . Тогда (12) выполняется для всех и для всех .
Тогда
.
Поскольку произвольно, то

Поэтому
.
То есть при уравнение
(5.m) .
принимает вид
(11) .

Доказательство единственности решения

Предположим, что уравнение
(4)
имеет два решения и , различающиеся в некоторой точке , принадлежащей интервалу .
Рассмотрим функцию
.
Тогда .
Поскольку и непрерывны, то и непрерывная функция. Поэтому она отлична от нуля в некотором интервале, содержащем точку :
при .
Поскольку , то . То есть точка не принадлежит этому интервалу.

Если , то преобразуем (4) следующим образом:
,
где
.
Если переобозначить постоянные
,
то получим задачу (4), для которой
;
при ,
где – некоторое число, не превосходящее .

Если , то поступаем аналогично:
,
Переобозначим постоянные:
.
Получаем задачу (4), для которой
;
при ,
где – некоторое число, не меньшее .

Итак, мы имеем:
;
при ( или при ).
Далее возьмем произвольное положительное число ( или ) и рассмотрим закрытый интервал ( или ). Поскольку функция непрерывна, то она достигает наибольшего значения в одной из точек этого интервала:
( или ).

Сделаем оценку, применяя уравнение (4) и условие Липшица:

.
Итак, мы получили оценку:
.
Поскольку , то разделим на :
.
Возникает противоречие, поскольку при это неравенство не выполняется.

Следовательно, не может иметь отличных от нуля значений. Поэтому . Что и требовалось доказать.

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.

Автор: Олег Одинцов . Опубликовано: 20-06-2016

Исследование СЛАУ. Общие сведения

В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.

Общие сведения (определения, условия, методы, виды)

Системы линейных алгебраических уравнений с n неизвестными могут иметь:

• единственное решение;
• бесконечное множество решение (неопределенные СЛАУ);
• ни одного решения (несовместные СЛАУ).

Пример 1

Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.

Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .

Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .

Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:

• Совместна ли система?
• Если система совместна, то, какое количество решений она имеет — одно или несколько?
• Как найти все решения?

Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:

• если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
• если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
• если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.

Ранг матрицы и его свойства

Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.

Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда

В математике выделяют следующие подходы к определению ранга матрицы:

• при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
• при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
• при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.

Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .

Свойства ранга матрицы:

1. квадратная невырожденная матрица обладает рангом, который отличается от нуля;
2. если транспонировать матрицу, то ранг матрицы не изменяется;
3. если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
4. при удалении нулевого столбца или строки ранг матрицы не изменяется;
5. ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
6. при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
7. ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
8. когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .

Пример 2

А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0

r ( A 1 ) = 1 , r ( B 1 ) = 1

А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6

Условия существования и единственности решения системы уравнений

Пусть задана неоднородная система линейных алгебраических уравнений размерности m × n .

Матрица называется расширенной матрицей системы, если наряду с коэффициентами при неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m × (n+1) .

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса , который основан на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае преобразования производятся по столбцам).

Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.

На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.

Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.

Если r = n , то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы .

Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.

1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:

2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов переменных системы (1.10) равно числу сочетаний из n элементов по r элементов C_n r . Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно C_n r .

Пусть строки матрицы обозначены соответственно l ₁ ; l ₂ ;…; l_n . Строка l называется линейной комбинацией строк l ₁ ; l ₂ ;…; l_n матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть , .

Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных ( r n ) . В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:

Так как r ( A ) =2 и , то по теореме 1.3 (Кронекера-Капелли) заданная система линейных алгебраических уравнений совместна. Количество переменных n =2 , т.е. r n , значит, система является неопределённой. Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов переменных: < x ₁ ; x ₂ >, < x ₁ ; x ₃ >, < x ₁ ; x ₄ >, < x ₂ ; x ₃ >, < x ₂ ; x ₄ >, < x ₃ ; x ₄ > . Рассмотрим один из них < x ₁ ; x ₂ > . Тогда систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

По формулам (1.6) имеем

Данное выражение базисных переменных через свободные представляет собой общее решение системы:

При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x ₃ = x ₄ = 17 . При x₃=0 x₄=0 получаем базисное решение системы