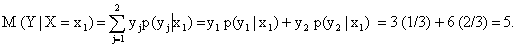Математика — онлайн помощь
Важной характеристикой условного распределения вероятностей является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины Y при X = x (x – определенное возможное значение X) называют произведение возможных значений Y на их условные вероятности:
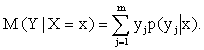
Для непрерывных величин
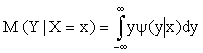
где 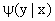
Условное математическое ожидание M (Y | x) есть функция от x:
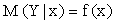
которую называют функцией регрессии Y на X.
Аналогично определяются условное математическое ожидание случайной величины X и функция регрессии X на Y: 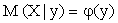
ПРИМЕР 13.1.58 Дискретная двумерная случайная величина задана таблицей
| Y\X | 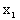 | 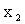 | 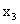 | 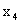 |
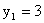 | 0,15 | 0,06 | 0,25 | 0,04 |
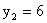 | 0,30 | 0,10 | 0,03 | 0,07 |
Найти условное математическое ожидание составляющей Y при 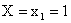
Решение. Найдем 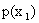
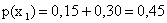
Найдем условное распределение вероятностей величины Y при 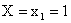
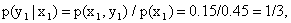
Найдем искомое условное математическое ожидание по формуле (13.1.50):
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Условные математические ожидания уравнения регрессии
6.5.3 хУМПЧОЩЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС. тЕЗТЕУУЙС
рХУФШ ЪБДБОП ЧЕТПСФОПУФОПЕ РТПУФТБОУФЧП ( W , F, P) Й УМХЮБКОЩК ЧЕЛФПТ (ξ1, ξ2) ОБ ОЕН.
пртедемеойе 6.5.3.1
хумпчощн нбфенбфйюеулйн пцйдбойен ПДОПК ЙЪ УМХЮБКОЩИ ЧЕМЙЮЙО, ЧИПДСЭЙИ Ч УЙУФЕНХ (ξ1, ξ2), ОБЪЩЧБЕФУС ЕЈ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ, ЧЩЮЙУМЕООПЕ РТЙ ХУМПЧЙЙ, ЮФП ДТХЗБС УМХЮБКОБС ЧЕМЙЮЙОБ РТЙОСМБ ПРТЕДЕМЕООПЕ ЪОБЮЕОЙЕ, ФП ЕУФШ ОБКДЕООПЕ ОБ ПУОПЧЕ ХУМПЧОПЗП ЪБЛПОБ ТБУРТЕДЕМЕОЙС.
еУМЙ (ξ1, ξ2) — УМХЮБКОЩК ЧЕЛФПТ ДЙУЛТЕФОПЗП ФЙРБ:
еУМЙ (ξ1, ξ2) — УМХЮБКОЩК ЧЕЛФПТ БВУПМАФОП ОЕРТЕТЩЧОПЗП ФЙРБ, У РМПФОПУФША ТБУРТЕДЕМЕОЙС 
пртедемеойе 6.5.3.2
хУМПЧОПЕ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ξ2 РТЙ ЪБДБООПН ЪОБЮЕОЙЙ УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1 = xk (ξ1 = x0) ОБЪЩЧБЕФУС тезтеууйек ξ2 ОБ xk(x 0 ).
хУМПЧОПЕ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1 РТЙ ЪБДБООПН ЪОБЮЕОЙЙ УМХЮБКОПК ЧЕМЙЮЙОЩ ξ2 = yj (ξ2 = y0) ОБЪЩЧБЕФУС тезтеууйек ξ1 ОБ yj(y 0 ).
зТБЖЙЛЙ ЬФЙИ ЪБЧЙУЙНПУФЕК ОБЪЩЧБАФУС МЙОЙСНЙ ТЕЗТЕУУЙЙ ЙМЙ ЛТЙЧЩНЙ ТЕЗТЕУУЙЙ.
дМС ОЕЪБЧЙУЙНЩИ УМХЮБКОЩИ ЧЕМЙЮЙО ξ1, ξ2 МЙОЙЙ ТЕЗТЕУУЙЙ ξ2 ОБ xk(x 0 ) Й ξ1 ОБ yj(y 0 ) РБТБММЕМШОЩ ЛППТДЙОБФОЩН ПУСН, ФБЛ ЛБЛ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ ЛБЦДПК ЙЪ ОЙИ ОЕ ЪБЧЙУЙФ ПФ ФПЗП, ЛБЛЙЕ ЪОБЮЕОЙС РТЙОСМБ ДТХЗБС УМХЮБКОБС ЧЕМЙЮЙОБ.
рХУФШ ЪБДБОП ЧЕТПСФОПУФОПЕ РТПУФТБОУФЧП ( W , F, P) Й УМХЮБКОЩК ЧЕЛФПТ (ξ1, ξ2, . , ξn) ОБ ОЕН.
пртедемеойе 6.5.3.3
хумпчощн нбфенбфйюеулйн пцйдбойен УМХЮБКОПК ЧЕМЙЮЙОЩ ξi РТЙ ХУМПЧЙЙ, ЮФП
ξ1 = x 0 1, ξ2 = x 0 2, . , ξi-1 = x 0 i-1, ξi+1 = x 0 i+1, . , ξn = x 0 n,
ОБЪЩЧБЕФУС НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ ξi, ЧЩЮЙУМЕООПЕ У ХЮЕФПН ХУМПЧОПЗП ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ.
зЕПНЕФТЙЮЕУЛЙ ТЕЗТЕУУЙС ЙОФЕТРТЕФЙТХЕФУС ЛБЛ РПЧЕТИОПУФШ Ч n-НЕТОПН РТПУФТБОУФЧЕ Й ОБЪЩЧБЕФУС РПЧЕТИОПУФША ТЕЗТЕУУЙЙ ξi ОБ
x 0 1, x 0 2, . , x 0 i-1, x 0 i+1, . , x 0 n .
тЕЗТЕУУЙС ОБЪЩЧБЕФУС МЙОЕКОПК, ЕУМЙ РПЧЕТИОПУФШ ТЕЗТЕУУЙЙ ПРЙУЩЧБЕФУС МЙОЕКОПК ЖХОЛГЙЕК. рТЙ n=2 МЙОЕКОБС ТЕЗТЕУУЙС — РТСНБС, РТЙ n=3 — РМПУЛПУФШ, n>3 — ЗЙРЕТРМПУЛПУФШ.
жПТНХМЩ ДМС ЧЩЮЙУМЕОЙС ХУМПЧОПЗП НБФЕНБФЙЮЕУЛПЗП ПЦЙДБОЙС УМХЮБКОЩИ ЧЕМЙЮЙО ξi Ч ЬФПН УМХЮБЕ ЧЩЧПДСФУС БОБМПЗЙЮОП ЖПТНХМБН (6.5.3.1-6.5.3.2).
ъбнеюбойе. фБЛ ЛБЛ ЧУЕ НПНЕОФЩ — ОБЮБМШОЩЕ Й ГЕОФТБМШОЩЕ — МАВЩИ РПТСДЛПЧ РТЕДУФБЧМСАФ УПВПК НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС, ФП НПЦОП ЗПЧПТЙФШ ПВ ХУМПЧОЩИ НПНЕОФБИ МАВПЗП РПТСДЛБ.
ъбдбюб 6.5.3.1 дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2):
 | 0 | 2 | 5 |
|---|---|---|---|
| 1 | 0,1 | 0 | 0,2 |
| 2 | 0 | 0,3 | 0 |
| 4 | 0,1 | 0,3 | 0 |
оБКФЙ ХУМПЧОЩЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1.
рТЕЦДЕ ЧУЕЗП ОБКДЕН ХУМПЧОЩЕ ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1.
| xk | 1 | 2 | 4 |
| pk | 0,1/0,2 = 0,5 | 0/0,2 = 0 | 0,1/0,2 = 0,5 |
| xk | 1 | 2 | 4 |
| pk | 0/0,6 = 0 | 0,3/0,6 = 0,5 | 0,3/0,6 = 0,5 |
| xk | 1 | 2 | 4 |
| pk | 0,2/0,2 = 1 | 0/0,2 = 0 | 0/0,2 = 0 |
ъбдбюб 6.5.3.2 йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1,ξ2) БВУПМАФОП ОЕРТЕТЩЧОПЗП ФЙРБ:
оБКФЙ ХУМПЧОЩЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ1.

ъБНЕФЙН, ЮФП t 2 + 2ty0 + 5y0 2 = (t + y0) 2 + 4y0 2 . уМЕДПЧБФЕМШОП,
рТЙ ТБУЮЕФБИ НЩ ХЮЙФЩЧБМЙ, ЮФП ЙОФЕЗТБМ ПФ ОЕЮЕФОПК ЖХОЛГЙЙ РП УЙННЕФТЙЮОПНХ РТПНЕЦХФЛХ ТБЧЕО ОХМА Й ЮФП
ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.
ъбдбюб 6.5.3.1(у) дБО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ (ξ1, ξ2):
 | 0 | 2 | 5 |
|---|---|---|---|
| 1 | 0,1 | 0 | 0,2 |
| 2 | 0 | 0,3 | 0 |
| 4 | 0,1 | 0,3 | 0 |
оБКФЙ ХУМПЧОЩЕ НБФЕНБФЙЮЕУЛЙЕ ПЦЙДБОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ2.
ъбдбюб 6.5.3.2(у) йЪЧЕУФОБ РМПФОПУФШ ТБУРТЕДЕМЕОЙС УМХЮБКОПЗП ЧЕЛФПТБ БВУПМАФОП ОЕРТЕТЩЧОПЗП ФЙРБ:
оБКФЙ ХУМПЧОПЕ НБФЕНБФЙЮЕУЛПЕ ПЦЙДБОЙЕ УМХЮБКОПК ЧЕМЙЮЙОЩ ξ2, ЕУМЙ ξ1 = x0.
© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002
Условные математические ожидания уравнения регрессии
Сразу же отметим, что эконометрическая модель н е обязательно является регрессионной, т.е. объясненная часть не всегда представляет собой условное математическое ожидание зависимой переменной. [c.12]
Условное математическое ожидание случайной величины Y при Х=х, т. е. Мх( Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по X аналогично Му(Х) называется функцией регрессии или просто регрессией X по Y. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессий) Г по Хи X по Y. [c.38]
В силу неоднозначности статистической зависимости между Y и X для исследователя, в частности, представляет интерес усредненная по X схема зависимости, т. е. закономерность в измерении условного математического ожидания МХ(У) или M(Y/X = x) (математического ожидания случайной переменной Y, вычисленного в предположении, что переменная X приняла значение х) в зависимости от х. [c.51]
Если зависимость между двумя переменными такова, что каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной. [c.51]
Иначе, корреляционной зависимостью между двумя переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. [c.51]
Доверительный интервал для функции регрессии. Построим доверительный интервал для функции регрессии, т.е. для условного математического ожидания M Y), который с заданной надежностью (доверительной вероятностью) у = 1— а накрывает неизвестное значение Mx(Y). [c.64]
Доверительный интервал для индивидуальных значений зависимой переменной. Построенная доверительная область для M Y) (см. рис. 3.6) определяет местоположение модельной линии регрессии (т.е. условного математического ожидания), но не отдельных возможных значений зависимой переменной, которые отклоняются от средней. Поэтому при определении доверительного интервала для индивидуальных значений у зависимой переменной необходимо учитывать еще один источник вариации — рассеяние вокруг линии регрессии, т.е. в оценку суммарной дисперсии s следует [c.67]
Оценим условное математическое ожидание Mx=g(Y). Выборочной оценкой MX=S( ) является групповая средняя j>x=8, которую найдем по уравнению регрессии [c.68]
Наряду с интервальным оцениванием коэффициентов регрессии по (4.23 ) весьма важным для оценки точности определения зависимой переменной (прогноза) является построение доверительного интервала для функции регрессии или для условного математического ожидания зависимой переменной Л/Х(У), найденного в предположении, что объясняющие переменные Х, Х2. Хр приняли значения, задаваемые вектором X Q =(l x10 x20. .. хр0). [c.98]
Решение. Выше, в примере 6.2, получено уравнение регрессии у, = 181,32 + 25,679 , т. е. ежегодно спрос на товар увеличивался в среднем на 25,7 ед. Надо оценить условное математическое ожидание Ml=9(Y) = y(9). Оценкой у(9) является групповая средняя [c.145]
Условные математические ожидания (для нормального распределения) 40 [c.305]
Условное математическое ожидание можно рассматривать как оператор проектирования в пространстве случайных величин. С другой стороны, с каждой случайной величиной можно связать оператор умножения на эту величину. Эти обстоятельства дают возможность распространить ряд понятий теории вероятностей на теорию линейных операторов в сепарабельном гильбертовом пространстве. [c.15]
Условным математическим ожиданием оператора А относительно подпространства L называется оператор PLA. Это условное математическое ожидание обладает свойствами обычного математического ожидания 1. PLA = А, если A L — измерим [c.15]
Условное математическое ожидание М, (х) называют еще [c.92]
В том случае, когда по экспериментальным данным д ,- определяется (прогнозируется) среднее значение yt применяются методы регрессионного анализа. Кривая зависимости условного математического ожидания [c.331]
Интеграл (х — x)Pv(dQ) называется условным математическим ожиданием слу- [c.19]
Целевая функция Qi(Xi) задачи t -ro этапа представляет собой условное математическое ожидание a )o( o , хп) при условии, что на этапах, предшествующих этапу i, реализован набор со 1 случайных параметров условий задачи и приняты решения, составляющие набор xi i, а на этапах, следующих за i-u, приняты оптимальные решения 196 [c.196]
Если вектор сп— (GI,. . сп) имеет совместное нормальное распределение, то условное математическое ожидание сп при фиксированном наборе с «1 представляет собой в соответствии с выводами п. 2.3 линейную комбинацию составляющих с»»1. [c.242]
Формула (4.8) сводит вопрос о получении характеристик оптимального фильтра к вычислению условного математического ожидания М[т] ] ( )] или условной вероятности [«nUU)]- [c.315]
Сигнал, спектральная плотность которого — дробно-рациональная функция частоты, можно представить как реакцию линейной системы на белый шум. Другими словами, такой сигнал может быть получен как решение линейного стохастического дифференциального уравнения, возмущаемого белым шумом. Случайный процесс — решение соответствующих стохастических дифференциальных уравнений — представляет собой марковский процесс или проекцию марковского процесса. Статистические характеристики марковских процессов — переходные вероятности — удовлетворяют известным дифференциальным уравнениям в частных производных А. Н. Колмогорова. Для вычисления условного математического ожидания М[т (0] гауссовского марковского процесса можно получить обыкновенное дифференциальное уравнение. Таким образом, выражение (4.8) для решения задачи (4.1) позволяет свести вычисление характеристик оптимальной в смысле задачи (4.1) фильтра- [c.315]
Условное математическое ожидание вагоно-часов накопления на состав при Т=к определится равенством [c.81]
Условное математическое ожидание формально записывается как [c.354]
Модель условного математического ожидания здесь будет моделью AR(2) и параметры регрессии следующие [c.357]
Предположим, что П,-Е (б) = s,t,u и что г = 1 (т. с. безрисковый процент равен пулю). Пусть Xj(s), ij(t) и Xj(u) — будущая стоимость акций фирмы j при данной информации на рынке. Тогда, как мы знаем, на нейтральном к риску рынке полностью выявляющие цепы акций фирмы j будут равны условному математическому ожиданию величины Xj, т. е. [c.120]
Подразумевая, как и прежде, под уср (X) — Е (г) = X) условное математическое ожидание результирующего показателя г) (при условии, что объясняющая переменная приняла значение, равное X), мы от (В. 17) приходим к линейному уравнению регрессии [c.40]
Из (В.21) непосредственно следует, что уравнение регрессии т] по g (т. е. вид зависимости условного математического ожидания f/ p (х) = Е (т = х) от х) совпадает со структурным соотношением (В.20)1. Однако в схеме Dlt в отличие от схем В и С, остаточная случайная компонента в разложениях [c.42]
В этих выкладках использовался способ вычисления математического ожидания в два этапа на первом фиксируются значения X и усреднение производится по значениям г) (при фиксированном X), т. е. берется условное математическое ожидание при условии, наложенном на на втором этапе результат усредняется по всевозможным значениям X (нижний индекс у знака математического ожидания показывает, по каким именно значениям производится усреднение). [c.88]
Первый случай. Данные разведки на момент анализа ее результатов указывают, что месторождение — непромышленное. Эта оценка, как и всякая оценка по выборке, содержит погрешность, и вероятность, что фактически месторождение является рентабельным, не равна нулю. Обозначим через М(С ) условное математическое ожидание прибыли от разработки такого месторождения, рассчитанное по данным п-го шага разведки. М(С ), по определению, является математическим ожиданием усеченного слева (в точке 0min, см. рис. 2.4.1) распределения оценки прибыли от разработки месторождения. На рис. 2.4.1 величина М(С ) пропорциональна заштрихованной площади под кривой / ( ), где — оценка критического параметра месторождения, определяющего прибыль. Тогда разведку следует прекратить в тот момент, когда будет выполнено неравенство [c.75]
Здесь t — число этапов хт = (x,, X2,. . . , XT) — вектор переменных (план) .. ., ыг) — вектор случайных событий M t pt(xt, ы ) ш 1 -условное математическое ожидание случайной вектор-функции
) — случайный вектор ограничений /-го этапа, зависящий от наблюдения вероятностных параметров на предыдущих t—l этапах Gt — детерминированное множество допустимых решений задачи на -м этапе. [c.59]
Обозначим a/f(xf, GJ ) =о,-,(шО — («О и вычислим значение условного математического ожидания MLJt[Qit(xt, oO W»1] в выражении (3.109). В соответствии с формулой (3.108) имеем [c.81]
Ejtw — влияние агрегированных факторов (неучтенных, неидентифицированных), условное математическое ожидание (УМО) которых в анализируемом периоде равно нулю. [c.114]
Здесь я — произвольный n-мерный вектор, принадлежащий множеству К — начальная точка процесса ps — величина шага на s-й итерации YS — нормирующий множитель gw — случайный вектор, условное математическое ожидание которого относительно х зависит линейно от обобщенного градиента срж (субградиента или опорного функционала) функции [c.181]
Обозначим, кроме того, через Мш ы(о>») mft 1 . условное математическое ожидание u(uift) в предположении, что известна реализация шй ф [c.193]
Для проверки адекватности модели GAR H необходимо проверить стандартизованные остатки е/а, где о — условное среднее квадратическое отклонение, рассчитываемое по модели GAR H и е — остатки в уравнении условного математического ожидания. Если модель GAR H достаточно хорошо определена, то стандартизованные остатки будут независимы и идентично распределены. Этот критерий проводится в два этапа. [c.360]
Итак, мы имеем т + 1 + р + q + 1 параметр для оценки (т + 1) значений альфа из уравнения условного математического ожидания, (р + 1) — бэта и q— гамма из уравнения условной дисперсии. [c.368]
Чтобы убедиться в этом, надо при вычислении условного математического ожидания от обеих частей соотношения (В.21) лишь учесть, что условие 5 — х равносильно условию ел. = 0, и, кроме того, воспользоваться естественным допущением Еву = Е (еу = х) = 0. [c.42]
http://cde.osu.ru/courses2/course8/p_6_5_3.html
http://economy-ru.info/info/5451/