Установить что каждое из следующих уравнений определяет параболу

Установить что каждое из следующих уравнений определяет параболу

Глава 20. Парабола

Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

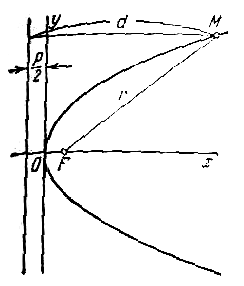
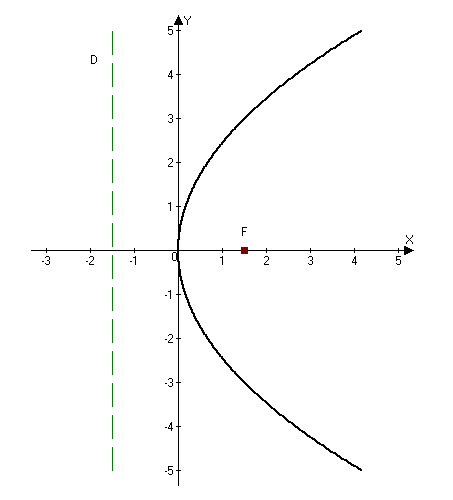
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

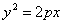
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

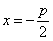
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

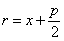
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

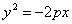
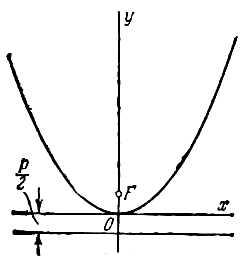
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

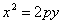
если она лежит в верхней полуплоскости (рис.), и

(4)

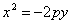
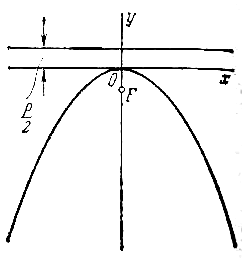
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

Уравнение у2 = 4х – 8 определяет параболу

Скачать
презентациюДекартова система координат в пространстве и на плоскости >>

Пример: Установить, что уравнение у2 = 4х – 8 определяет параболу, и найти координаты ее вершины А, величину параметра р и уравнение директрисы. у2 = 4х – 8 Представим уравнение в каноническом виде: у2 = 4(х — 2) вершина параболы смещена вдоль оси ОХ вправо на две единицы. А(2;0) – координаты вершины параболы. 2р = 4 р = 2 – параметр параболы. 3. — уравнение директрисы параболы.

Слайд 29 из презентации «Декартова система координат» к урокам геометрии на тему «Векторы в пространстве»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке геометрии, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Декартова система координат.ppt» можно в zip-архиве размером 204 КБ.

Векторы в пространстве

«Решение задач координатным методом» — Угол. Решите задачу. Введите прямоугольную систему координат. Варианты. Найдите расстояние. Решение задач на нахождение расстояний и углов. Ромб. Тексты задач. Отрезки. Отрезки в плоскости основания. Алгоритм решения задач. Стороны основания. В основании многогранника. Точка. Составьте уравнение плоскости.

«Вектор имеет координаты» — Вершина. Координаты конца единичного вектора. Найдите координаты. Векторы. Координаты вектора. Найдите длину вектора. Координаты равны нулю. Длина вектора. Угол между векторами. Найдите координаты точки. Найдите координаты векторов. Прямоугольный параллелепипед. Координаты. Теорема. Вектор. Длина.

«Прямоугольная система координат» — Координаты точек пространства. Декарт. Сфера радиуса. Начало координат. Координаты точки. Координаты. Геометрическое место точек. Найдите координаты. Геометрическое место. Точка. Центр нижнего основания куба. Ребро. Прямоугольная система координат. Координаты середины отрезка.

«Декартова система координат» — Фокальное расстояние. Аналитическое уравнение эллипса. Уравнение прямой с угловым коэффициентом. Условия параллельности и перпендикулярности двух прямых. Общее уравнение линии второго порядка на плоскости. Прямые на плоскости. Упорядоченные координатные оси, не лежащие в одной плоскости. D – директриса параболы.

«Определение компланарных векторов» — Определение. Цели урока. Фронтальный опрос. Компланарные векторы. Мы умеем на плоскости складывать векторы по правилу треугольника. Признак компланарности трех векторов. Справедливо ли утверждение. Новый материал. Устное решение. Может ли длина суммы двух векторов быть меньше длины каждого. Так как векторы компланарны, то они лежат в одной плоскости.

«Понятие вектора в пространстве» — Понятие вектора появилось в 19 веке. Записать все термины по теме «Векторы на плоскости». Определение коллинеарности векторов. Кроссворд. Коллинеарные векторы. Современная символика для обозначения вектора. MNPQ- квадрат. Равенство векторов. Любая точка пространства также может рассматриваться как вектор.

Всего в теме «Векторы в пространстве» 23 презентации

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home

Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Эллипс.

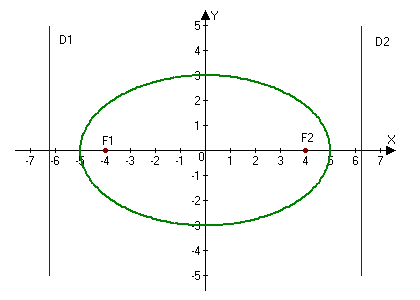
Эллипс с каноническим уравнением $\frac+\frac=1, a\geq b>0,$ и меет форму изображенную на рисунке.

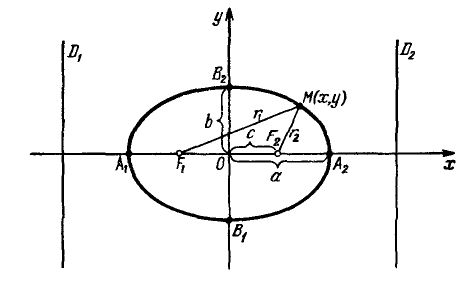
Параметры $a$ и $b$ называются полуосями эллипса (большой и малой соответственно). Точки $A_1(-a, 0),$ $A_2(a, 0), $ $B_1(0, -b), $ и $B_2(0, b), $ его вершинами. Оси симметрии $Ox$ и $Oy$ — главными осями а центр симметрии $O -$ центром эллипса.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt\geq 0,$ называются фокусами эллипса векторы $\overline$ и $\overline -$ фокальными радиус-векторами, а числа $r_1=|\overline|$ и $r_2=|\overline| -$ фокальными радиусами точки $M,$ принадлежащей эллипсу. В частном случае $a=b$ фокусы $F_1$ и $F_2$ совпадают с центром, а каноническое уравнение имеет вид $\frac+\frac=1,$ или $x^2+y^2=a^2,$ т.е. описывает окружность радиуса $a$ с центром в начале координат.

Прямые $D_1: x=-a/e$ и $D_2: x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами эллипса.

Теорема. ( Директориальное свойство эллипса)

Эллипс является множеством точек, отноше ние расстояний от которых до фокуса и до соответствующей директрисы постоянно и равно $e.$

Примеры.

2.246. Построить эллипс $9x^2+25y^2=225.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения директрис.

Приведем уравнение эллипса к каноническому виду:

а) Находим полуоси $a=5,$ $b=3.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt:$

$c=\sqrt<5^2-3^2>=\sqrt<16>=4\Rightarrow F_1(-4, 0),\qquad F_2(4, 0).$

г) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=5,$ $b=3;$ б) $ F_1(-4, 0),\qquad F_2(4, 0);$ в) $e=\frac<4><5>;$ г) $D_1: x=-\frac<25><4>$ и $D_2: x=\frac<25><4>.$

2.249 (a). Установить, что уравнение $5x^2+9y^2-30x+18y+9=0$ определяет эллипс, найти его центр $C,$ полуоси, эксцентриситет и уравнения директрис.

Приведем уравнение эллипса к каноническому виду, для этого выделим полные квадраты:

Это уравнение эллипса. Центр имеет координаты $C=(x_0, y_0)=(-3, -1);$ полуоси $a=3,$ $b=\sqrt 5.$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac<3><2/3>=-\frac<9> <2>$ и $D_2: x=\frac<3><2/3>=\frac<9><2>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(x_0, y_0)=(-3, -1);$ $a=3,$ $b=\sqrt 5;$ $ e=\frac<2><3>.$ $D_1:2x+3=0, $ $D_2: 2x-15=0.$

2.252. Эллипс, главные оси которого совпадают с координатными осми, проходят через точки $M_1(2, \sqrt 3)$ и $M_2(0, 2).$ Написать его уравнение, найти фокальные радиусы точки $M_1$ и расстояния этой точки до директрис.

Решение.

Поскольку оси эллипса совпадают с координатными осями, то центр эллипса совпадает с началом координат. Следовательно, из того, что точка $(0, 2)$ принадлежит эллипсу, можно сделать вывод, что $b=2.$

Далее, чтобы найти $a,$ подставим найденное значение $b$ и координаты точки $M_1(2, \sqrt 3)$ в каноническое уравнение эллипса $\frac+\frac=1:$

Таким образом, уравнение эллипса $\frac<16>+\frac<4>=1.$

Далее найдем координаты фокусов:

$c=\sqrt=\sqrt<16-4>=2\sqrt 3\Rightarrow F_1(-2\sqrt 3, 0),\,\,\, F_2(2\sqrt 3, 0).$

Отсюда находим $\overline =(2+2\sqrt 3, \sqrt 3),$ $\overline=(2-2\sqrt 3, \sqrt 3).$

Чтобы найти расстояния от точки $M_1$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Таким образом, расстояние от точки $M_1(2, \sqrt 3)$ до прямой $D_1: \sqrt 3 x+8=0$

расстояние от точки $M_1(2, \sqrt 3)$ до прямой $D_2: \sqrt 3 x-8=0$

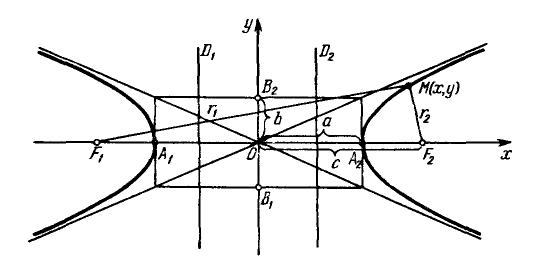
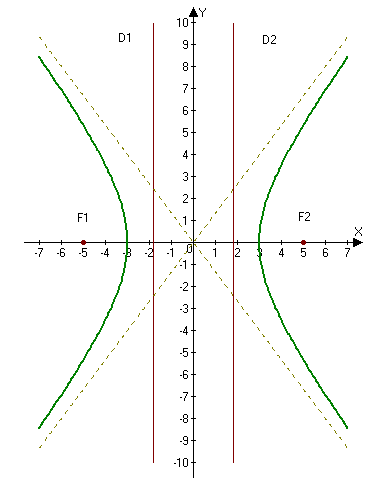
Параметры $a$ и $b$ называются полуосями гиперболы. Точки $A_1(-a, 0),$ $A_2(a, 0) — $ ее вершинами. Оси симметрии $Ox$ и $Oy$ — действительной и мнимой осями а центр симметрии $O -$ центром гиперболы.

Точки $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt\geq 0,$ называются фокусами гиперболы, векторы $\overline$ и $\overline -$ фокальными радиус-векторами, а числа $r_1=|\overline|$ и $r_2=|\overline| -$ фокальными радиусами точки $M,$ принадлежащей гиперболе.

Прямые $D_1: x=-a/e$ и $D_2:x=a/e,$ перпендикулярные главной оси и проходящей на расстоянии $a/e$ от центра, называются директрисами гиперболы.

Теорема. (Директориальное свойство гиперболы).

Гипербола является геометрическим местом точек, отношение расстояний от которых до фокуса и до соответствующей дирек трисы постоянно и равно $e.$

Примеры.

2.265. Построить гиперболу $16x^2-9y^2=144.$ Найти: а) полуоси; б) координаты фокусов; в) эксцентриситет; г) уравнения асимптот; д) уравнения директрис.

Приведем уравнение гиперболы к каноническому виду:

а) Находим полуоси $a=3,$ $b=4.$

б) Фокусы найдем по формулам $F_1(-c, 0)$ и $F_2(c, 0),$ где $c=\sqrt:$

$c=\sqrt<3^2+4^2>=\sqrt<25>=5\Rightarrow F_1(-5, 0),\qquad F_2(5, 0).$

г) Асимптоты гиперболы находим по формулам $y=\pm\fracx:$

д) Уравнения директрис находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

Ответ: а) $a=3,$ $b=4;$ б) $ F_1(-5, 0),\qquad F_2(5, 0);$ в) $e=\frac<5><3>;$ г) $y=\pm\frac<4><3>x;$ д ) $D_1: x=-\frac<9><5>$ и $D_2: x=\frac<9><5>.$

2.269 (a). Установить, что уравнение $16x^2-9y^2-64x-54y-161=0$ определяет гиперболу, найти ее центр $C,$ полуоси, эксцентриситет, уравнения асимптот и директрис.

Приведем заданное уравнение к каноническому виду, для этого выделим полные квадраты:

Это уравнение гиперболы. Центр имеет координаты $C=(x_0, y_0)=(2,-3);$ полуоси $a=3,$ $b=4.$

Асимптоты гиперболы c центром в начале координат, находим по формулам $y=\pm\fracx,$ а с центром в точке $C=(x_0, y_0) -$ по формуле $y-y_0=\pm\frac(x-x_0),$

$$y+3=\frac<4><3>(x-2)\Rightarrow 3y+9=4x-8\Rightarrow 4x-3y-17=0.$$

$$y+3=-\frac<4><3>(x-2)\Rightarrow 3y+9=-4x+8\Rightarrow 4x+3y+1=0.$$

Уравнения директрис для эллипса с центром в начале координат находим по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac<3><5/3>=-\frac<9> <5>$ и $D_2: x=\frac<3><5/3>=\frac<9><5>.$ Поскольку у заданного эллипса центр смещен, то директриссы будут иметь уравнения $D_1: x=x_0-a/e$ и $D_2: x=x_0+a/e:$

Ответ: $C=(2, -3);$ $a=3,$ $b=4;$ $ e=\frac<5><3>,$ $4x-3y-17=0,$ $4x+3y+1=0,$ $D_1:5x-1=0, $ $D_2: 5x-19=0.$

2.272. Убедившись, что точка $M(-5, 9/4)$ лежит на гиперболе $\frac<16>-\frac<9>=1,$ найти фокальные радиусы этой точки и расстояния этой точки до директрис.

Решение.

Проверим, что заданная точка лежит на гиперболе:

Следовательно, точка $M(-5, 9/4)$ лежит на гиперболе $\frac<16>-\frac<9>=1.$

Для того, чтобы найти фокальные радиусы, найдем фокусы гиперболы:

$c=\sqrt\Rightarrow c=\sqrt<16+9>=\sqrt <25>=5$ Следовательно, фокусы имеют координаты $F_1(-5, 0), F_2(5, 0).$

Фокальные радиусы точки, можно найти по формулам $r_1=|\overline|$ и $r_2=|\overline|.$

Чтобы найти расстояния от точки $M$ до директрис, найдем уравнения директрис по формулам $D_1: x=-a/e$ и $D_2: x=a/e:$

$D_1: x=-\frac<4><5/4>\Rightarrow x=-\frac<16><5>\Rightarrow 5x+16=0;$

$D_2: x=\frac<4><5/4>\Rightarrow x=\frac<16><5>\Rightarrow 5x-16=0;$

Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac<\sqrt>\right|.$$

Таким образом, расстояние от точки $M(5, 9/4)$ до прямой $D_1: \sqrt 5x+16=0$

расстояние от точки $M(5, 9/4)$ до прямой $D_2: \sqrt 5x-16=0$

Ответ: $r_1=9/4,$ $r_2=\frac<41><4>;$ $d_1=\frac<41><5>;$ $d_2=\frac<9><5>.$

2.273. Найти точки гиперболы $\frac<9>-\frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1.$

Решение.

Из уравнения гиперболы находим полуоси: $a=3, \, b=4.$ Следовательно, $c=\sqrt\Rightarrow c=\sqrt<9+16>=\sqrt <25>=5.$

Отсюда находим $F_1=(-5, 0).$

Геометрическое место точек, расположенных на расстоянии $7$ от фокуса $F_1,$ это окружность с центром в точке $F_1=(-5, 0)$ и радиусом $r=7:$

Чтобы н айти точки гиперболы $\frac<9>-\frac<16>=1,$ находящиеся на расстоянии $7$ от фокуса $F_1,$ решим систему уравнений

Решим уравнение $5x^2+18x-72=0:$

Находим соответствующие координаты $y:$ $y_1=\pm\sqrt<24-2,4^2-10\cdot 2,4>=\sqrt<-5,76>$ — нет корней .

Ответ: $(-6, \pm4\sqrt 3).$

Парабола.

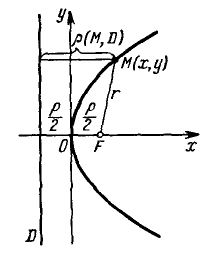
Парабола с каноническим уравнением $y^2=2px, p>0,$ и меет форму изображенную на рисунке.

Число $p$ называется параметром параболы. Точка $O -$ ее вершиной, а ось $Ox$ — осью параболы.

Точка $F\left(\frac

<2>, 0\right)$ называется фокусом параболы, вектор $\overline -$ фокальным радиус-векторам, а число $r=|\overline| -$ фокальным радиусом точки $M,$ принадлежащей параболе.

Прямая $D: x=-p/2$ перпендикулярная оси и проходящая на расстоянии $p/2$ от вершины параболы, называется ее директрисой.

Примеры.

2.285 (а). Построить параболу $y^2=6x$ и найти ее параметры.

Решение.

Параметр $p$ параболы можно найти из канонического уравнения $y^2=2px: $

$$y^2=6x\Rightarrow y^2=2\cdot 3x\Rightarrow p=2.$$

Ответ: $p=3.$

2.286 (а). Написать уравнение параболы с вершиной в начале координат, если известно, что парабола расположена в левой полуплоскости, симметрично относительно оси $Ox$ и $p=1/2.$

Решение.

Поскольку парабола расположена в левой полуплоскости, симметрично относительно оси $Ox,$ то уравнение параболы будет иметь вид $y^2=-2px.$ Подставляя заданное значение параметра, находим уравнение параболы:

Ответ: $y^2=-x.$

2.288 (а). Установить, что уравнение $y^2=4x-8$ определяет параболу, найти координаты ее вершины $A$ и величину параметра $p.$

Решение.

Уравнение параболы, центр которой сдвинут в точку $(x_0, y_0),$ имеет вид $(y-y_0)^2=2p(x-x_0)^2.$

Приведем заданное уравнние к такому виду:

Таким образом, $y^2=4(x^2-2)$ — парабола с центром в точке $(0, 2).$ Параметр $p=2.$

Ответ: $C(0, 2),$ $p=2.$

2.290. Вычислить фокальный параметр точки $M$ параболы $y^2=12x,$ если $y(M)=6.$

Решение.

Чтобы найти фокальный параметр точки $M,$ найдем ее координаты. Для этого подставим в уравнение параболы координату $y:$ $$6^2=12x\Rightarrow 36=12x\Rightarrow x=3.$$

Таким образом, точка $M$ имеет координаты $(3, 6).$

Из уравнения параболы $y^2=12x$ находим параметр параболы: $y^2=2\cdot 6x\Rightarrow p=6.$ Следовательно фокус параболы имеет координаты $F(3, 0).$

Далее находим фокальный параметр точки:

Ответ: $6.$

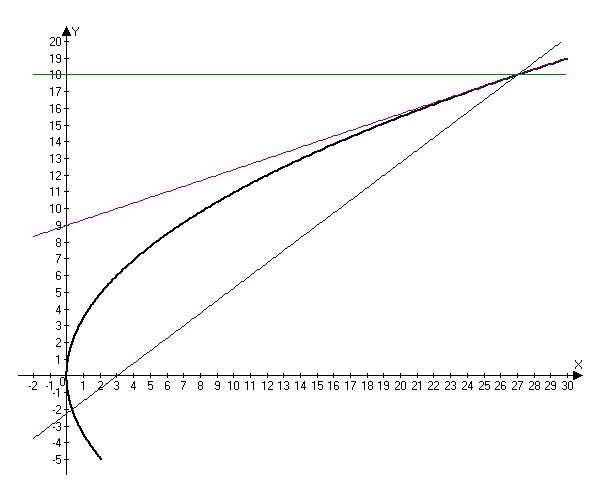
2.298. Из фокуса параболы $y^2=12x$ под острым углом $\alpha$ к оси $Ox$ направлен луч света, причем $tg\alpha=\frac<3><4>.$ Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

Решение.

Найдем координаты фокуса. Из канонического уравнения параболы $y^2=2px$ находим параметр: $y^2=12x=2\cdot 6x\Rightarrow p=6.$

Координаты фокуса $F(p/2, 0)\Rightarrow F(3,0).$

Далее находим уравнение прямой, которая проходит через точку $(3, 0)$ под углом $\alpha: tg\alpha=\frac<3><4>$ к оси $OX.$ Уравнение ищем в виде $y=kx+b,$ где $k=tg\alpha=\frac<3><4>.$

Чтобы найти $b,$ в уравнение прямой подставим координаты точки $(3, 0):$

$0=\frac<3><4>\cdot 3+b\Rightarrow b=-\frac<9><4>.$ Таким образом, уравнение луча, направленного из фокуса $y=\frac<3><4>x-\frac<9><4>.$

Далее, найдем точку пересечения найденной прямой с параболой:

Поскольку по условию луч падает под острым углом, то мы рассматриваем только положительную координату $y=18.$ Соответствующее значение $x=\frac<18^2><12>=\frac<324><12>=27.$

Таким образом, луч пересекает параболу в точке $(27, 18).$

Далее найдем уравнение касательной к параболе в найденной точке $(27, 18)$ по формуле $(y-y_0)=y'(x_0)(x-x_0):$

Подставляем все найденные значения в уравнение касательной:

$y-18=\frac<1><3>(x-27)\Rightarrow 3y-54=x-27\Rightarrow x-3y+27=0.$

Далее, найдем угол $\beta$ между лучем $y=\frac<3><4>x-\frac<9><4>$ и касательной $x-3y+27=0.$ Для этого оба уравнения запишем в виде $y=k_1x+b_1$ и $y=k_2+b_2$ угол вычислим по формуле $tg(L_1, L_2)=\frac<1+k_1\cdot k_2>$

$$L_2: x-3y+27=0\Rightarrow y=\frac<1><3>x+9\Rightarrow k_2=\frac<1><3>.$$

Легко увидеть, что угол между лучем $L_1,$ направленным из фокуса и его отражением равен $\pi-2\beta,$ а угол между отраженным лучем и осью $Ox$ $\pi-(\pi-2\beta)-\alpha=2\beta-\alpha.$

Зная $tg\beta=\frac<1><3>$ и $tg\alpha=k_1=\frac<3><4>$ и вспоминая формулы для двойного угла тангенса и тангенс разности, находим $tg(2\beta-\alpha):$

$$tg(2\beta-\alpha)=\frac<1+tg2\beta tg\alpha>=\frac<\frac<3><4>-\frac<3><4>><1+\frac<3><4>\frac<3><4>>=0.$$ Следовательно, прямая, содержащая отраженный луч параллельна оси $Ox.$ Так как она проходит через точку $(27, 18),$ то можно записать ее уравнение $y=18.$