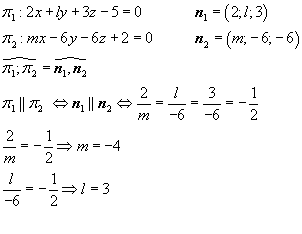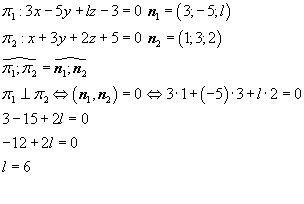Установить какие из следующих пар уравнений перпендикулярные плоскости

Уравнение плоскости

Задача 1

Составить уравнение плоскости, которая проходит через начало координат перпендикулярно вектору (5;0-3)

Ответ: 5х-3z=0

Задача 2

Составить уравнение плоскости, проходящей через точку (3;4;-5) параллельно векторам: (3;1;-1); (1;-2;1)

Ответ: x+4y+7z+16=0

Задача 3

Установить какие из следующих пар уравнений прямых параллельны плоскости:

1) 2x-3y+5z-7=0; 2x-3y+5z+3=0

2) 4x+2y-4z+5=0; 2x+y+2z-1=0

Ответ:1 – параллельны, 2 – не параллельны, 3 –не параллельны

Задача 4

Определить при каком значении L следующие пары уравнений будут задавать перпендикулярные плоскости:

1) 3х-5у+Lz-3=0; x+3y+2z+5=0

2) 5x+y-3z-3=0; 2x+Ly-3z+1=0

Ответ: 1) L=6; 2) L=-19

Задача 5

Составить уравнение плоскости, которая проходит через (3;-2;-7) параллельно плоскости

Ответ: 2x-3z-27=0

Задача 6

Составить уравнение плоскости, которая проходит через (2;-1;1) перпендикулярно к двум плоскостям:

Ответ: x+2z-4=0

Задача 7

Плоскость проходит, через (6;-10;1) и отсекает на оси абсцисс отрезок

а=-3, на оси опликат с=2. Составить для плоскости уравнение в отрезках.

Ответ: + + =1

Задача 8

Найти расстояние от Р(-1;1;-2) до плоскости, проходящей через 3 точки:

1) (1;-1;1)

2) (-2;1;3)

3) (4;-5;-2)

Ответ: 4.

Блок «Прямые в пространстве»

Задача 1

Составить канонические уравнения прямой, проходящей через точку (2;0;-3) параллельно:

1) Вектору a=

2) Прямой -= =

Ответ:

· 1) -= =

· -= =

· -= =

· -= =

· -= =

Задача 2

Составить параметрические уравнения прямой, проходящей через данные точки:

Ответ:

Задача 3

Через точки (-6;6;-5) и (12;-6;1) проведена прямая. Определить точки пересечения этой прямой с координатными плоскостями.

Ответ:(9;-4;0), (3;0;-2), (0;2;-3)

Задача 4

Найти острый угол между прямыми -= = , -= =

Ответ:

Задача 5

Найти проекцию точки P (2;-1;3) на прямую x=3t, y=5t-7, z=2t+2

Ответ: (3;-2;4)

Задача 6

При каких значениях L и C прямая = = перпендикулярна к плоскости 3x-2y+Cz+1=0

Ответ:L=-6, C=

Задача 7

Найти точку Q, симметричную точке P (4;1;6) относительно прямой x-y-4z+12=0, 2x+y-2z+3=0

Ответ:Q (2;-3;2)

Задача 8

Найти точку Q, симметричную точке P (2;-5;7) относительно прямой, проходящей через точки (5;4;6) и (-2;-17;-8)

Ответ: Q (4;1;-3)

Задача 9

Найти проекцию точки P (5;2;-1) на плоскость 2x-y+3z+23=0

Ответ:(1;4;-7)

Задача 10

Вычислить кратчайшее расстояние между двумя прямыми в каждом из следующих случаев:

1) -= = ; -= =

2) x=2t-4, y=-t+4, z=-2t-1

3) -= = ;

Ответ:

Задача 10

Cоставить канонические и параметрические уравнения прямой

Ответ:

Блок «Эллипс»

Задача 1

Составить уравнение эллипса, фокусы которого лежат на оси абсцисс симметрично относительно начала координат, зная, кроме того что:

1. Его полуоси равны 5 и 2;

2. Его большая ось равна 10, а расстояние между фокусами 2с=8;

3. Его малая ось равна 24, а расстояние между фокусами 2с=10;

4. Расстояние между его фокусами 2с=6 и эксцентриситет =3/5;

5. Его большая ось равна 20, а эксцентриситет =3/5;

6. Его малая ось равна 10, а эксцентриситет =12/13;

7. Расстояние между его директрисами равно 5 и расстояние между фокусами 2с=4;

8. Его большая ось равна 8, а расстояние между директрисами равно 16.

9. Его малая ось равна 6, а расстояние между директрисами равно 13;

10. Расстояние между его директрисами равно 32 и =1/2

Ответ:

1.

2.

3.

4.

5.

6.

7.

8.

9. или

10.

Задача 2

Составить уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, кроме того, что:

· Его полуоси равны соответственно 7 и 2;

· Его большая ось равна 10, а расстояние между фокусами 2с=8;

· Расстояние между его фокусам 2с=24 и эксцентриситет =12/13;

· Его малая ось равна 16, а эксцентриситет =3/5;

· Расстояние между его фокусами 2с=6 и расстояние между директориями равно 50/3;

· Расстояние между его директрисами равно 32/3 и эксцентриситет .

Ответ:

1.

2.

3.

4.

5.

6.

Задача 3

Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны точки М₁( и М₂( эллипса.

Ответ:

Задача 4

Установить, что каждое из следующих уравнений определяет эллипс, и найти координаты его центра С, полуоси, эксцентриситет и уравнения директрис:

· 5x 2 +9y 2 -30x+18y+9=0;

· 16x 2 +25y 2 +32x-100y-284=0;

· 4x 2 +3y 2 -8x+12y-32=0

Ответ:

· C(3;-1) ; уравнение директрис 2x-15=0, 2x+3=0;

· C(-1;2) ; уравнение директрис 3x-22=0, 3x+28=0;

· C(1;-2) ; уравнение директрис y-6=0, y+10=0

Блок «Гипербола»

Задача 1

Составить уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, кроме того, что:

· Её оси 2a=10 и 2b=8;

· Расстояние между фокусами 2c=10 и ось 2b=8;

· Расстояние между фокусами 2c=6 и эксцентриситет = ;

· Ось 2a=16 и эксцентриситет = ;

· Уравнения асимптот и расстояние между фокусами 2c=20;

· Расстояние между директрисами равно и расстояние между фокусами 2c=26;

· Расстояние между директрисами равно и ось 2b=6;

· Расстояние между директрисами равно и эксцентриситет = ;

· Уравнения асимптот и расстояние между директрисами

равно .

Ответ:

·

·

·

·

·

·

·

·

·

Задача 2

Составить уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, кроме того, что:

· Её полуоси a=6, b=18 (буквой “a” мы обозначаем полуось гиперболы, расположенную на оси абсцисс);

· Расстояние между фокусами 2c=10 и эксцентриситет = ;

· Уравнения асимптот и расстояние между вершинами равно 48.

· Расстояние между директрисами равно и эксцентриситет = ;

· Уравнения асимптот и расстояние между директрисами

равно .

Ответ:

·

·

·

·

Задача 3

Установить, что каждое из следующих уравнений определяет гиперболу, и найти координаты её центра C, полуоси, эксцентриситет, уравнения асимптот и уравнения директрис:

1) 16 -9 -64x-54y-161=0

2) 9 -16 +90x+32y-367=0

3) 16 -9 -64x-18y+199=0

Ответ:

1)C(2;-3), a=3, b=4, 5/3, уравнения директрис: 5х-1=0, 5х-19=0, уравнения асимптот: 4x-3y-17=0, 4x+3y+1=0;

2)C(-5;1), a=8, b=6, =1,25, уравнения директрис : x=-11,4 и x=1,4, уравнения асимптот: 3x+4y+11=0 и 3x-4y+19=0

3) C(2;-1), a=3, b=4, =1,25 , уравнения директрис: y= -4,2 , y=2,2 , уравнения асимптот: 4x+3y-5=0, 4x-3y-11=0

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.044 сек.)

Установить какие из следующих пар уравнений перпендикулярные плоскости

№ 1

Найти угол между плоскостями

2x — 4y + 4z — 5 = 0 и -3x +2y + 4z — 5 = 0 .

Решение

Угол между плоскостями определяется углом между соответствующими векторами нормалей к этим плоскостям. Координаты вектора нормали плоскости легко можно определить из общего уравнения плоскости, — это коэффициенты при переменных.

№ 2

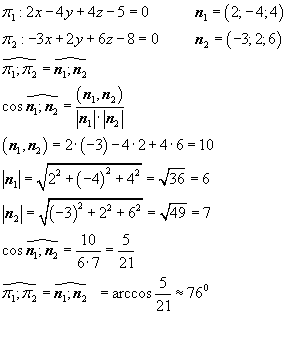
Определить, при каких значениях l и m пара уравненеий

2 x + l y + 3 z — 5 = 0

m x — 6 y — 6 z + 2 = 0

будет определять параллельные плоскости.

Решение

Плоскости параллельны тогда и только тогда, когда векторы нормалей плоскостей коллинеарны:

№ 3

Определить, при каком значении l пара уравненеий

3 x — 5 y + l z — 3 = 0

x + 3 y + 2 z + 5 = 0

будет определять перпендикулярные плоскости.

Решение

Плоскости перпендикулярны тогда и только тогда, когда векторы нормалей плоскостей перпендикулярны, следовательно, их скалярное произведение равно нулю:

Установить какие из следующих пар уравнений перпендикулярные плоскости

а) Направляющий вектор прямой имеет координаты a = (3; 3; -5), нормальный вектор плоскости — n = (7; -2; 3). Векторы, очевидно, не коллинеарны; следовательно, прямая не перпендикулярна плоскости. Проверим условие (2) параллельности прямой и плоскости:

Условие выполняется. Данные прямая и плоскость параллельны.

б) В данном случае а = (2; 3; 4) и n = (1; -1; 1). Векторы не коллинеарны, поэтому условие (3) не выполняется. Проверим условие (2) параллельности прямой и плоскости:

Условие не выполняется. Прямая и плоскость не параллельны и, следовательно, пересекаются. Для определения координат точки пересечения нужно решить систему трех уравнений с тремя неизвестными:

Такую систему удобно решать, предварительно записав уравнения прямой в параметрическом виде:

Подставляя значения х, у и z в уравнение плоскости, получим

откуда t = 1 и, значит, х = 2, у = 4, z = 5. Прямая и плоскость пересекаются в точке (2; 4; 5).

в) За направляющий вектор прямой возьмем векторное произведение векторов
n₁=(6; 3;-2) и n₂ = (6; 1; 2), т. е. нормальных векторов, задающих данную прямую. Найдем его координаты:

$$ a=[n_1; n_2]=\begin i & j & k \\ 6 & 3 & -2 \\ 6 & 1 & 2 \end=8i-24j-12k $$

Нормальный вектор n данной плоскости имеет координаты (2; -6; -3). Условие (3) перпендикулярности прямой и плоскости выполнено, так как

Данные прямая и плоскость перпендикулярны. Для определения точки пересечения прямой и плоскости запишем уравнения прямой в параметрическом виде. Направляющий вектор прямой уже найден, это вектор а = (8; -24; -12) или ему коллинеарный вектор (2; -6; -3). Осталось найти какую-нибудь точку прямой. Положим х = 0, тогда

откуда у = 13, z = 9. Точка (0; 13; 9) принадлежит прямой. Следовательно, параметрические уравнения прямой имеют вид

Подставляя значения х, у и z в уравнение плоскости, получим

4t — 6(13 — 6t) — 3 (9 — 3t) — 91 = 0

или 49t = 196, t = 4. Точка прямой, получающаяся при значении параметра t = 4, принадлежит плоскости. Прямая и плоскость пересекаются в точке (8; -11; -3).