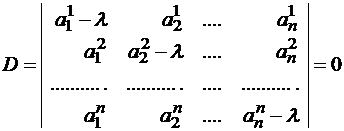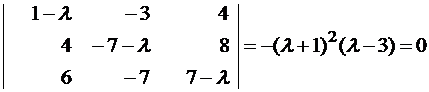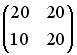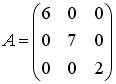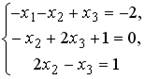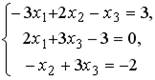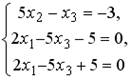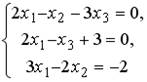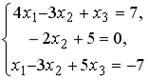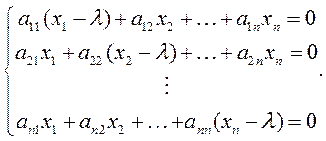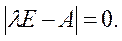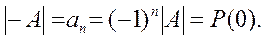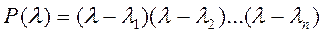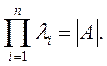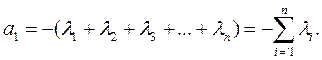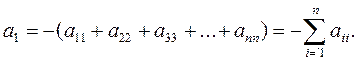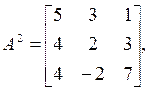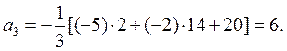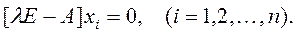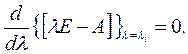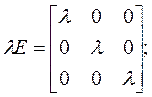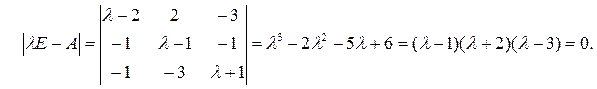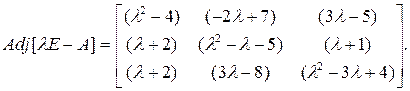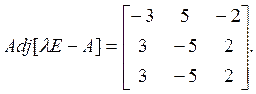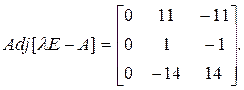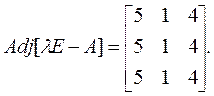Установите соответствие между матрицами и их характеристическими уравнениями

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 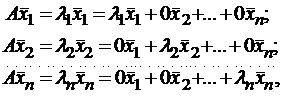тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса — собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n — координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)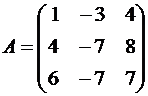
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x — собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

Системы линейных уравнений, методы решения.

ДАС

2.Матрицы, основные понятия и определения.

3.Линейные операции над матрицами.

5.Системы линейных уравнений, основные понятия.

6.Системы линейных уравнений, методы решения.

7.Основные задачи аналитической геометрии на плоскости.

8.Прямая на плоскости.

9.Кривые второго порядка.

10.Прямая и плоскость в пространстве.

11.Функции, основные понятия и определения.

13.Геометрический и физический смысл производной.

14.Производные первого порядка.

15.Производные высших порядков.

16.Приложения дифференциального исчисления ФОП.

17.Дифференциальное исчисление ФНП.

18.Приложения определённого интеграла.

19.Типы дифференциальных уравнений.

20.ДУ первого порядка.

21.ДУ высших порядков.

22.Линейные дифференциальные уравнения 2-го порядка.

Вычисление определителей.

1.1.Установите соответствие между матрицей и ее определителем.
1. ; 2. ; 3.

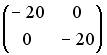
0; 400; — 400; 200; — 200.

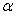
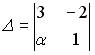
1.2.Установите соответствие между и значениями определителей .
1. 4 2. 4 3. ;4. .

; ; ; ; ; .

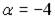
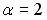
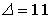
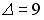
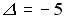
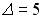
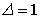
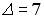
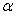
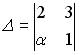
1.3.Установите соответствие между и значениями определителей .
1. ; 2. ; 3. ; 4. .

; ; ; ; ; .

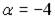
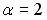
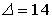
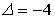
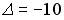
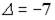
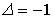
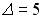
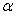
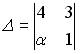
1.4.Установите соответствие между и значениями определителей .
1. ; 2. ; 3. ; 4. .

; ; ; ; ; .

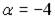
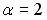
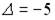
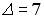
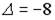
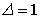
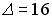
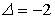
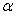
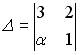
1.5.Установите соответствие между и значениями определителей .
1. ; 2. ; 3. ; 4. .

; ; ; ; ; .

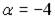
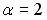
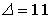
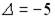
2.Матрицы, основные понятия и определения.

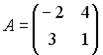
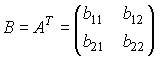
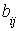
2.1. Даны матрица и транспонированная матрица . Установите соответствие между элементами транспонированной матрицы и элементами матрицы А

1. ; 2. ; 3. ; 4. . – 3; — 2; 3; 2; 1; 4.

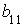
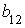
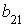
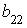
2.2.Установите соответствие между матрицами и их рангами.
1) ; 2) ; 3) ; 4) .

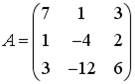
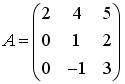
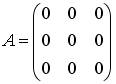
2.3.Установите соответствие между матрицами и их рангами.
1) ; 2) ; 3) ; 4)

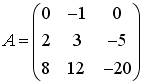
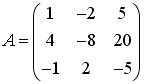
2.4.Установите соответствие между матрицами и их рангами.
1) ; 2) ; 3) ; 4)

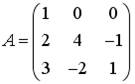
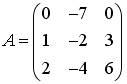
2.5.Дана матрица . Установите соответствие между указанными элементами и их алгебраическими дополнениями.

1) ; 2) ; 3) ; 4) .

; ; ; ; ; .

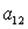
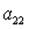
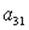
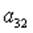
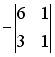
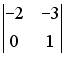
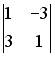
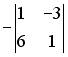
Линейные операции над матрицами.

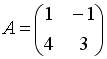
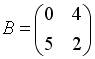
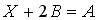
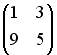
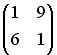
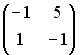
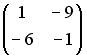
3.1. Даны матрицы и . Тогда решением матричного уравнения является матрица …

; ; ; .

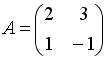
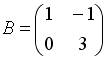
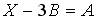
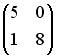
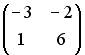
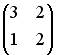
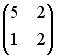
3.2.Даны матрицы и . Тогда решением матричного уравнения является матрица …

; ; ; .

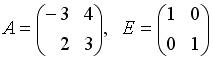
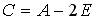
3.3.Если , то значение определителя матрицы равно …: 3; — 14; — 3; — 13.

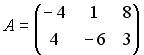
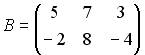
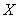
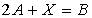
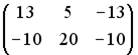
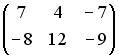
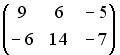
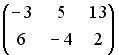
3.4.Даны матрицы и . Тогда матрица , являющаяся решением уравнения , равна …

; ; ; .

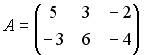
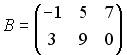
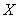
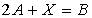
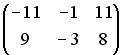
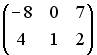
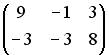
3.5.Даны матрицы и . Тогда матрица , являющаяся решением уравнения , равна …

; ; ; .

Умножение матриц.

4.1. Операция произведения матриц правильно определена для матричного умножения вида …

; ; ;

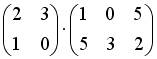
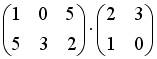
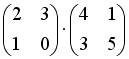
4.2. Операция произведения матриц правильно определена для матричного умножения вида …

; ; ;

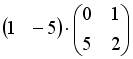
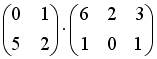
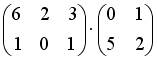
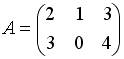
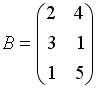
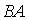
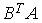
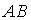
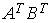
4.3. Для матриц и и транспонированных к ним определены произведения … ; ; ; ;

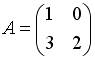
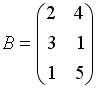
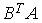
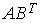
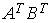
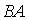
4.4. Для матриц и и транспонированных к ним определены произведения … ; ; ; ;

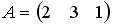
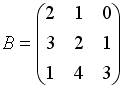
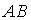
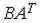
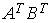
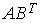
4.5. Для матриц и и транспонированных к ним определены произведения … ; ; ; ;

5.Системы линейных уравнений, основные понятия.

5.1. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. ;2. ;3. ;4.

; ; ; ; ; .

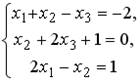
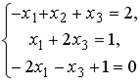
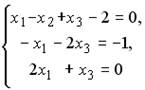
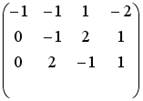
5.2.Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 2. 3. 4.

; ; ; ;

; .

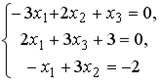
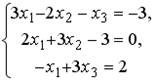
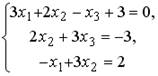
5.3.Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. ;2. ;3. ;4.

; ; ; ;

; .

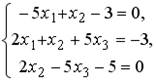
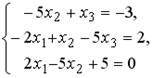
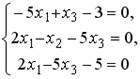
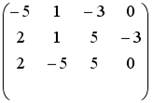
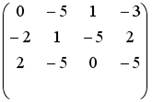
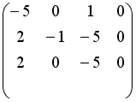
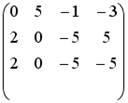
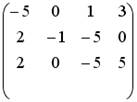
5.4.Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. ;2. ;3. ;4.

; ; ; ;

; .

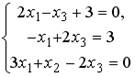
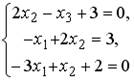
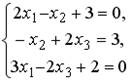
5.5.Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. ;2. ;3. ;4.

; ; ; ;

; .

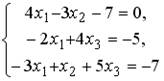
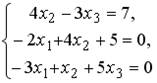
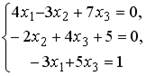
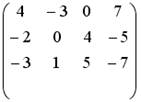
Системы линейных уравнений, методы решения.

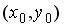
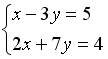
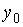
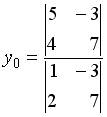
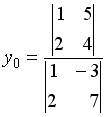
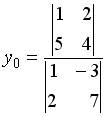
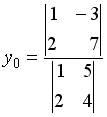
6.1. Если – решение системы линейных уравнений , то может определяться по формуле…

; ; ; .

6.2.Дана система линейных уравнений 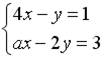. Система не имеет решений при а равном:…-8; 8; 5; -5.

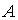
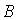
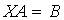
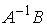
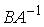
6.3.Пусть и – обратимые квадратные матрицы одного порядка. Тогда решением матричного уравнения является матрица…

; ; ; .

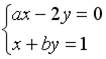
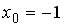
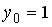
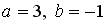
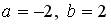
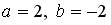
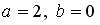
6.4.Система линейных уравнений имеет решение , при …

; ; ; .

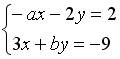
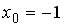
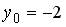
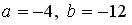
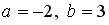
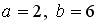
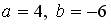
6.5.Система линейных уравнений имеет решение , при: ; ; ; .

Характеристические числа и характеристические векторы

От характеристических векторов зависят динамические свойства системы. Рассмотрим векторное уравнение

где у – вектор входа (n×1); x – вектор выхода (n×1); А – квадратная матрица (n×n).

Вопрос о нахождении характеристических значений связан с вопросом: существует ли такой вектор x, который в результате его преобразования с помощью матрицы А переходит в вектор y, имеющий то же направление в пространстве что и вектор x. Если такой вектор x существует, то это значит, что yпропорционален x(рис. 2.11):

y = Ax = λx,

Рис. 2.11. Характеристический вектор y= λx

Перенесем λx = λExв левую часть:

(λE – A)x= 0,

где E – единичная матрица.

Это векторно-матричное уравнение можно записать в виде равносильной системы скалярных уравнений, соответствующих строкам матрицы А:

Данная система имеет нетривиальное решение в том случае, если определитель матрицы коэффициентов равен нулю:

Раскрытие данного определителя приводит к характеристическому уравнению:

.

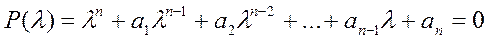
Многочлен n-й степени относительно l называется характеристическим многочленомматрицы А.Корни этого уравнения равны характеристическим (собственным) значениям матрицы А. Особый интерес представляют коэффициенты многочлена а₁ и а_n.

Если положить λ = 0, то:

и снова положим, что λ = 0. Тогда

,

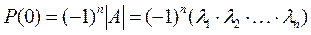
Таким образом, произведение характеристических чисел равно определителю матрицы А. В случае равенства нулю какого-нибудь из характеристических чисел матрица А становится особенной (вырожденной).

Раскрывая характеристическое уравнение, записанное в виде произведения сомножителей, можно выразить коэффициенты при различных степенях λ через характеристические числа.

Выразим коэффициент при λ n -1 :

С другой стороны, раскрывая также определитель |λE–A|, найдем, что коэффициент при λ n -1 равен со знаком минус сумме диагональных элементов матрицы А:

Таким образом, сумма диагональных элементов квадратной матрицы равна сумме ее характеристических чисел:

Ввиду важности этого свойства сумме диагональных элементов матрицы присвоено особое название: след матрицы. Обозначим след матрицы:

Формула Бохера

Можно записать полезную рекуррентную формулу, выражающую коэффициенты характеристического уравнения через следы матриц различного порядка T_k = Tr(A k ):

Эта формула, известная как формула Бохера, эффективна при вычислении коэффициентов характеристического уравнения с помощью компьютерной программы.

Пример. Найти характеристические числа следующей заданной матрицы А:

.

По формуле Бохера: a₁ = – T₁= – (2+1–1)= – 2. Произведение матрицы А на себя:

Следовательно, характеристическое уравнение имеет вид:

Модальная матрица

Для каждого из n характеристических чисел λ_i (i=1,2,…,n) матрицы А (в предположении, что все они различны) можно получить решение уравнения [λE –A]x = 0. Это векторно-матричное уравнение можно представить в виде системы уравнений

Векторы x_i, представляющие собой решения данной системы уравнений, являются характеристическими векторами матрицы A. Поскольку эта система уравнений однородная, то и k_ix_i, где k_i – произвольная скалярная величина, также служит решением. Поэтому эта система уравнений определяет однозначно только направление каждого из x_i.

Матрица, образованная векторами-столбцами k_ix_i, называется модальной матрицей. (Модальная – от слова “mode”, означающего «частота». Так называемые «частоты», описывающие динамику линейной системы, могут быть выражены в виде составляющих движения вдоль характеристических векторов).

При различных характеристических числах столбцы модальной матрицы могут выбираться равными или пропорциональными произвольному столбцу присоединенной матрицы Adj[λE – A].

Это вытекает из того факта, что [λE – A] имеет ранг n – 1. Поскольку определитель |λE – A|=0 (как мы уже выяснили), ранг матрицы Adj[λE– A] должен быть меньше n, однако при этом он не может быть меньше n – 1, так как тогда равнялись бы нулю все (n – 1) миноров строки определителя |λE– A|, что, в свою очередь, потребовало бы, чтобы

Отсюда следует, что λ_i является кратным корнем исходной системы уравнений, а это противоречит предположению о том, что характеристические числа различны. Таким образом, матрица [λE – A] имеет ранг (n – 1), поэтому из определения присоединенной матрицы следует, что столбцы модальной матрицы пропорциональны произвольному ненулевому столбцу Adj [λE – A]. Ввиду линейной зависимости столбцов Adj [λE – A] для данного λ_i выбор каждого λ_i определяет только один столбец модальной матрицы.

Пример. Найти характеристические числа и модальную матрицу, соответствующую матрице А:

.

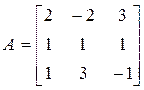
Характеристическое уравнение находим из условия |λE –A|=0:

Чтобы найти модальную матрицу, необходимо в присоединенную матрицу подставить значение собственных (характеристических) чисел.

При λ₁ = 1присоединенная матрица равна

При λ₂ = –2присоединенная матрица равна

При λ₃ = 3присоединенная матрица равна

Поскольку характеристические векторы единственным образом определяют только направление, то умноженные на скалярную величину, они также будут удовлетворять уравнению

.

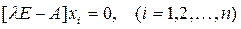
Следовательно, модальная матрица имеет вид:

Каждый столбец данной модальной матрицы служит характеристическим вектором в одномерном векторном пространстве. Три столбца модальной матрицы образуют базисв соответствующем трехмерном векторном пространстве.

Выше рассматривалась модальная матрица при различных характеристических числах А. В случае кратных характеристических чисел и несимметрической А определение независимых модальных столбцов не очевидно, так как не существует однозначного соответствия между порядком кратности корня характеристического уравнения и дефектом соответствующей характеристической матрицы [λE–A]. Однако и в этом случае вопрос построения модальной матрицы решается положительно, хотя и более сложно.