Эффективное решение квадратных уравнений. Приемы устного решения.
методическая разработка по алгебре (8 класс) на тему
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. В работе представлены устные приёмы, которые позволяют очень быстро и рационально решать квадратные уравнения: свойства коэффициентов и способ «переброски» старшего коэффициента. Овладение приемами поможет обучающимся экономить время, эффективно решать уравнения, развить математические, интеллектуальные способности, навыки исследовательской работы. Данный материал можно использовать на уроках, факультативных занятиях.
Скачать:
| Вложение | Размер |
|---|---|
| Эффективное решение квадратных уравнений. Приемы устного решения. | 1.55 МБ |
Предварительный просмотр:
Федеральное государственное казенное
«Средняя общеобразовательная школа №151»
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, иррациональных уравнений и неравенств.
Одна из основных целей изучения школьного курса математики заключается в овладении способами решения алгебраических уравнений второй степени и приводимых к ним уравнений. В школьном курсе изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения. Желательно научить ребят решать квадратные уравнения несколькими способами. Впоследствии при решении других видов уравнений, сводящихся к квадратным, рационально использовать те способы, которые позволяют находить корни квадратных уравнений устно: свойства коэффициентов и способ «переброски» старшего коэффициента.
Данные приемы устного решения квадратных уравнений заслуживают внимания, поскольку не отражены в школьном учебнике математики. Овладение приемами поможет обучающимся экономить время, эффективно решать уравнения, развить математические, интеллектуальные способности, навыки исследовательской работы.
Рассмотрим некоторые приемы устного решения квадратных уравнений.
- Приведенные квадратные уравнения.
Наиболее распространенное устное решение приведенных квадратных уравнений, но и оно у многих учеников вызывает затруднение, особенно в случаях, когда корни имеют разные знаки.
Напомним, что приведенное квадратное уравнение это уравнение вида
Корни х 1 и х 2 удовлетворяют теореме Виета
Определить знаки корней без решения уравнения (при условии, D • 0)
Статья по математике «Устный способ решения квадратных уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Устный способ решения квадратных уравнений.
( из опыта работы учителя математики МКОУ Началовская СОШ Россошанского района, Воронежской области Антоновской Аллы Ивановны)
Особое внимание при изучении темы «Квадратные уравнения» в 8 классе должно быть уделено выработке умений решать квадратные уравнения, разлагать квадратный трехчлен на множители и решать задачи методом составления квадратных уравнений. Вместе с тем достаточно серьезное внимание следует уделить и теоретическим вопросам: учащиеся должны уметь выводить формулу корней квадратного уравнения, доказывать теорему Виета и тождество ax 2 + bx + c = a ( x – x 1 )( x – x 2 ). Изучение этой темы продолжается в 9, 10 и 11 классах при решении биквадратных уравнений, неравенств второй степени, при решении тригонометрических, показательных, логарифмических уравнений, а также при решении текстовых и геометрических задач.
Работая много лет в старших классах, я нашла простой (устный) способ решения некоторых квадратных уравнений и назвала его «Решение квадратных уравнений по сумме коэффициентов».
Например: уравнение 24 x 2 +3 x – 27 =0 , используя этот метод, можно решить устно. Но каким образом? Об этом вы узнаете чуть позже.
Мои ученики с удовольствием этим способом пользуются, поэтому я хочу поделиться своим опытом с коллегами.
Рассмотрим примеры устного решения квадратных уравнений, используя теорему Виета.
D = 25 -16 =9, 9 – положительное число, значит уравнение имеет
два различных действительных корня.
Это приведенное квадратное уравнение, значит x 1 + x 2 =5, а x 1 x 2 = 4, так как произведение корней положительное число, то корни имеют одинаковые знаки, кроме того сумма корней также положительное число, значит, оба корня положительны. Нетрудно догадаться, что x 1 =1 и x 2 =4.
Так как -8 четное число, то D 1 =16 – 15 = 1, 1- положительное число, поэтому уравнение имеет два различных действительных корня.
Чтобы применить теорему Виета, преобразуем данное уравнение к виду x 2 — 

x 1 + x 2 =



Однако, решив уравнение обычным способом, т.е. через D 1 , получаем, что x 1 = 1, а x 2 =
Решая аналогичные приведенные и не приведенные уравнения, в которых сумма всех коэффициентов равна 0 ( a + b + c =0), можно заметить, что D или D 1 всегда > 0( поэтому такие уравнения всегда имеют два различных действительных корня) и один из корней равен 1, а второй равен коэффициенту c (если уравнение приведенное ) или 
Этот устный метод я предлагаю рассмотреть учащимся после того, как изучены все способы решения квадратных уравнений и, необходимо, как можно быстрее найти только корни квадратного уравнения, а процесс нахождения D или D 1 и корней квадратного уравнения можно опустить, чтобы сэкономить больше времени на решение данного основного уравнения, неравенства, на решение текстовой или геометрической задачи.
Решить уравнение 
Чтобы решить данное уравнение, сначала надо решить квадратное уравнение -5 x 2 +8 x -2= x или -5 x 2 +7 x -2 = 0. Так как сумма коэффициентов равна 0, т.е. -5 +7 -2 =0 и уравнение не приведенное, то x 1 =1 и x 2 =


Решить уравнение 4 x – 5*2 x + 4 =0.
Сделаем замену переменной t =2 x , тогда 4 x = (2 x ) 2 = t 2 . Данное уравнение принимает вид t 2 — 5 t + 4 =0. Так как сумма коэффициентов равна 0, т.е. 1 – 5+ 4 =0 и уравнение приведенное, то t 1 =1 и t 2 =4. Решая уравнения 2 x =1 и 2 x =4, получаем x =0 и x =2. Ответ: 0; 2.
Используя этот способ решения квадратных уравнений, учителю легко составить задания для самостоятельной работы в 8 классе (когда детям устный способ еще не известен) и проверить работы учеников.
Приведу несколько различных квадратных уравнений, которые можно решить устно.
а) x 2 + 35 x – 36 =0, так как 1+35 -36 =0, то x 1 = 1 и x 2 =-36.
б) x 2 — 17 x + 16 =0, так как 1 – 17 + 16 =0, то x 1 = 1 и x 2 =16.
в) 41 x 2 + 2 x – 43 =0, так как 41+ 2 – 43 =0, то x 1 = 1 и x 2 =-

Ответ: -1
г) — 37 x 2 + 19 x +18 =0, так как -37 + 19 + 18 =0, то x 1 = 1 и x 2 = — 
Ответ: — 
д) это уравнение я предлагала решить устно в начале своей статьи
24 x 2 +3 x – 27 =0, так как 24 + 3 – 27 =0, то x 1 = 1 и x 2 =-

Ответ: -1 
Уважаемые коллеги! Я надеюсь, что данные рекомендации помогут вам в дальнейшей работе. Желаю Вам больших творческих успехов!
Реферат: Способы устного решения квадратных уравнений
| Название: Способы устного решения квадратных уравнений Раздел: Остальные рефераты Тип: реферат Добавлен 01:30:00 06 сентября 2011 Похожие работы Просмотров: 2480 Комментариев: 14 Оценило: 4 человек Средний балл: 4 Оценка: неизвестно Скачать |
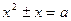 ) умели решать вавилоняне (около 2 тыс. лет до н.э.). Об этом свидетельствуют найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений могли решать древнегреческие математики, сводя их решения к геометрическим построениям. Приёмы решения уравнений без обращения к геометрии даёт Диофант Александрийский (III в.). В дошедших до нас 6 из 13 книг «Арифметика» содержатся задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получить решение уравнения вида ах= b или
) умели решать вавилоняне (около 2 тыс. лет до н.э.). Об этом свидетельствуют найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений могли решать древнегреческие математики, сводя их решения к геометрическим построениям. Приёмы решения уравнений без обращения к геометрии даёт Диофант Александрийский (III в.). В дошедших до нас 6 из 13 книг «Арифметика» содержатся задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получить решение уравнения вида ах= b или 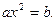 Способ решения полных квадратных уравнений не сохранились.
Способ решения полных квадратных уравнений не сохранились.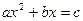 , где
, где 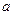 >0, дал индийский учёный Брахмагупта (VII в.). В трактате «Китаб аль-джебр Валь-мукабала» хорезмский математик аль-Хорезми разъясняет приёмы уравнений вида
>0, дал индийский учёный Брахмагупта (VII в.). В трактате «Китаб аль-джебр Валь-мукабала» хорезмский математик аль-Хорезми разъясняет приёмы уравнений вида 
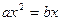 ,
, 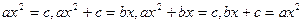 (буквами а, b и с обозначены лишь положительные числа, так как отрицательных чисел тогда не признавали) и отыскивает только положительные корни.
(буквами а, b и с обозначены лишь положительные числа, так как отрицательных чисел тогда не признавали) и отыскивает только положительные корни.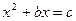 , было сформулировано немецким математиком М.Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Однако своё утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А.Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.
, было сформулировано немецким математиком М.Штифелем (1487-1567). Выводом формулы решения квадратных уравнений общего вида занимался Виет. Однако своё утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал). После трудов нидерландского математика А.Жирара (1595-1632), а также Декарта и Ньютона способ решения квадратных уравнений принял современный вид.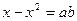 являются числа а и b .
являются числа а и b .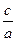 ,
,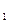 = –
= – 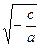 и х
и х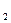 =
=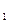 =
= 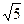 или х
или х 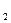 = –
= –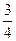 .
.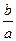 .
.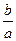 . Значит, неполное квадратное уравнение вида ах 2 + bx = 0 при b ≠ 0 всегда имеет два корня.
. Значит, неполное квадратное уравнение вида ах 2 + bx = 0 при b ≠ 0 всегда имеет два корня.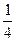 .
.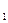 = 0, х
= 0, х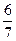 х –
х – 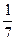 = 0.
= 0.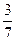 х , прибавим к ней выражение
х , прибавим к ней выражение 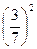 и вычтем его. Получим
и вычтем его. Получим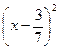 =
= 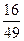 .
. или х –
или х – 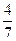 или х –
или х – 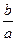 х +
х +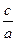 = 0.
= 0.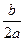 , прибавим к ней выражение
, прибавим к ней выражение 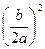
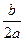 +
+ 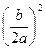 –
–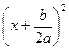 =
= 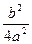 –
–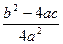 .
.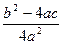 . Так как а ≠ 0, то 4а
. Так как а ≠ 0, то 4а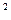 –положительное число, поэтому знак этой дроби определяется знаком его числителя, т. е. выражения b
–положительное число, поэтому знак этой дроби определяется знаком его числителя, т. е. выражения b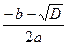 и х
и х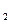 =
= 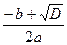 .
.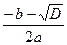 =
=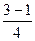 =
=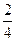 = 0,5
= 0,5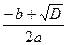 =
=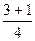 =
=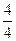 = 1
= 1 – 4ас= 6
– 4ас= 6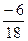 = – 0,3
= – 0,3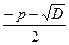 и х
и х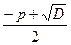 .
.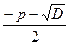 +
+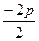 = –p ;
= –p ;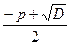 =
=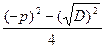 =
=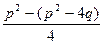 =
=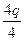 = q .
= q .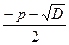 .
.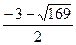 ; х
; х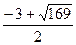 .
.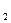 =
=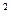 – 4ас= 4
– 4ас= 4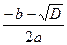 =
=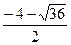 = – 5.
= – 5.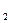 =
=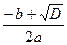 =
=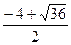 = 1.
= 1.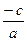 .
.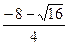 = –3.
= –3.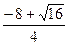 = –1.
= –1. Если а ±b + c ≠0, то используется прием переброски:
Если а ±b + c ≠0, то используется прием переброски: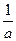 .
.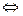
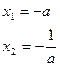
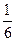 .
.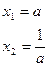
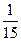 .
.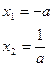
 .
.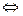

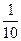 .
.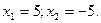 х = –5.
х = –5.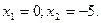
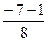 =
= 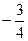 ;
;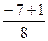 = –1.
= –1.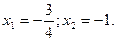
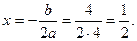
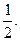
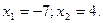
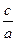 . а+ b + c = 0, х
. а+ b + c = 0, х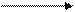 а) 6х 2 – 7х –3= 0.
а) 6х 2 – 7х –3= 0.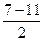 =
=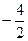 = –2;
= –2; =
=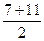 =
= 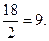
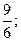 х2 =
х2 =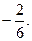
 б) 2х 2 – 11х +15= 0,
б) 2х 2 – 11х +15= 0, =
=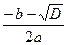 =
=
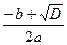 =
=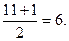
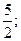 х2 = 3.
х2 = 3. х
х