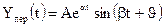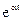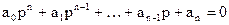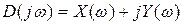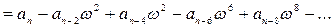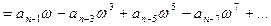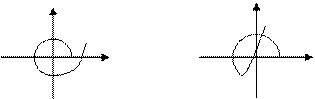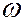Устойчивость сау по корням характеристического уравнения

Оценка устойчивости САУ по корням характеристического уравнения

При оценке устойчивости необходимо рассмотреть три возможных случая.

1. Корни вещественны.

2. Пары комплексно-сопряженных корней.

3. Корни чисто мнимые.

Если все корни вещественные и отрицательные, то есть

хсв(t) 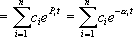. (3.6)

Если все корни вещественные и отрицательные, то каждое слагаемое хсв в формуле (3.6) стремится к нулю при t®¥ и, следовательно, хсв(t) ® 0, то есть необходимое и достаточное условие устойчивости (3.2) выполнено и САУ устойчива.

Если все корни вещественные, но среди них имеется хотя бы один положительный корень р _к = a _к > 0 , то соответствующее ему слагаемое в (3.6) будет иметь вид с_к exp(a_кt) и будет стремиться к ¥ при t®¥.

При этом, хотя все слагаемые в хсв(t) , кроме одного, будут затухать, переходный процесс САУ в целом будет расходящимся, а САУ — неустойчивой.

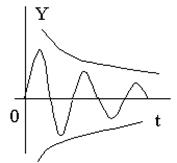
Если все корни вещественные, отрицательные и есть пара комплексно- сопряженных корней р _k =-a+jb . р _k+1=-a-jb. Тогда комплексным корням в Хсв(t) соответствуют слагаемые А= с_к exp[-(a-jb)t] и B= с_к exp[-(a+jb)t]. C учётом формул Эйлера можно записать

А+В= De -a t sin(bt+j). (3.7)

Сумма слагаемых, соответствующих комплексно-сопряжённым корням, представляет собой гармоническую функцию с угловой частотой b и амплитудой De -a t .

Параметр a — это параметр затухания огибающей k – кривой переходного процесса.

при a 0

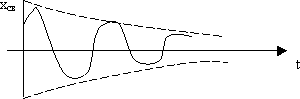
Таким образом, если действительная часть комплексного корня a

Алгебраический критерий устойчивости Гурвица детально рассмотрен в [1] на с. 47-48. Назначение, описание и особенности применения частотных критериев устойчивости линейных САУ приведены на с. 48-54 [1].

Вопросы для самопроверки

1. В чем состоит задача линеаризации уравнения системы автоматического регулирования (САР)?

2. Дайте понятия “устойчивой” и “неустойчивой” САР.

3. Что такое “принцип аргумента”?

4. Сформулируйте и поясните критерий устойчивости Найквиста-Михайлова для замкнутых систем.

5. Какие точки на годографе САР считаются “характерными”? Как они определяются?

6. Как влияет на устойчивость САР звено задержки?

7.Как влияет на устойчивость САР форсирующее звено?

8. Как влияет на устойчивость САР интегрирующее звено?

9. Для чего может использоваться в САР дополнительное интегрирующее звено?

Устойчивость сау по корням характеристического уравнения

8.1. Понятие устойчивости системы

Под устойчивостью системы понимается способность ее возвращаться к состоянию установившегося равновесия после снятия возмущения, нарушившего это равновесие. Неустойчивая система непрерывно удаляется от равновесного состояния или совершает вокруг него колебания с возрастающей амплитудой.

Устойчивость линейной системы определяется не характером возмущения, а структурой самой системы (рис.61). Говорят, что система устойчива «в малом» , если определен факт наличия устойчивости, но не определены ее границы. Система устойчива «в большом» , когда определены границы устойчивости и то, что реальные отклонения не выходят за эти границы.

В соответствии с классическим методом решение дифференциального уравнения ищется в виде:

y(t) = y вын (t) + y св (t).

Здесь yсв(t) — общее решение однородного дифференциального уравнения , то есть уравнения с нулевой правой частью:

a o y (n) + a 1 y (n-1) + . + a _(n-1) y’ + a _(n) y = 0.

Физически это означает, что все внешние воздействия сняты и система абсолютно свободна, ее движения определяются лишь собственной структурой. Поэтому решение данного уравнения называется свободной составляющей общего решения. y вын (t) — частное решение неоднородного дифференциального уравнения , под которым понимается уравнение с ненулевой правой частью. Физически это означает, что к системе приложено внешнее воздействие u(t) . Поэтому вторая составляющая общего решения называется вынужденный . Она определяет вынужденный установившийся режим работы системы после окончания переходного процесса.

Можно провести аналогию между САУ и пружиной, колебания которой описываются аналогичным дифференциальным уравнением (рис.62). Оттянем пружину, а затем отпустим, предоставив ее самой себе. Пружина будет колебаться в соответствии со свободной составляющей решения уравнения, то есть характер колебаний будет определяться только структурой самой пружины. Если в момент времени t = 0 подвесить к пружине груз, то на свободные колебания наложится внешняя сила Р . После затухания колебаний, описываемых только свободной составляющей общего решения, система перейдет в новый установившийся режим, характеризуемый вынужденной составляющей y вын = y(t ) . Если внешнее воздействие само будет изменяться по синусоидальному закону P = P _o sin(t + ) , то после затухания переходного процесса система будет совершать вынужденные колебания с той же частотой, что и вынуждающая сила, то есть y вын = y _max sin(t + y).

Каждая составляющая общего решения уравнения динамики ищется отдельно. Вынужденная составляющая ищется на основе решения уравнения статики для данной системы для времени t . Свободная составляющая представляет собой сумму из n отдельных составляющих: , где p _i корни характеристического уравнения D(p) = a ₀ p _n + a 1 p _n -1 + a 2 p _n -2 + . + a n = 0 . Корни могут быть либо вещественными p _i = a _i , либо попарно комплексно сопряженными p _i = a _i ± ji . Постоянные интегрирования А _i определяются исходя из начальных и конечных условий, подставляя в общее решение значения u, y и их производные в моменты времени t = 0 и t .

Каждому отрицательному вещественному корню соответствует экспоненциально затухающая во времени составляющая y св (t) _i , каждому положительному — экспоненциально расходящаяся, каждому нулевому корню соответствует y св (t) i = const (рис.63). Пара комплексно сопряженных корней с отрицательной вещественной частью определяет затухающие колебания с частотой i , при положительной вещественной части — расходящиеся колебания, при нулевой — незатухающие (рис.64).

Так как после снятия возмущения y вын (t) = 0 , то устойчивость системы определяется только характером свободной составляющей y св (t) . zПоэтому условие устойчивости систем по Ляпунову формулируется так: в устойчивой системе свободная составляющая решения уравнения динамики, записанному в отклонениях, должна стремиться к нулю, то есть затухать.

Исходя из расположения на комплексной плоскости корни с отрицательными вещественными частями называются левыми , с положительными — правыми (рис.65).

Поэтому условие устойчивости линейной САУ можно сформулировать следующим образом: для того, чтобы система была устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми. Если хотя бы один корень правый, то система неустойчива. Если один из корней равен нулю (в системах, где a n = 0 ), а остальные левые, то система находится на границе апериодической устойчивости . Если равны нулю вещественные части одной или нескольких пар комплексно сопряженных корней, то система находится на границе колебательной устойчивости .

Правила, позволяющие судить о знаках корней характеристического уравнения без его решения, называются критериями устойчивости . Их можно разделить на алгебраические (основаны на составлении по данному характеристическому уравнению по определенным правилам алгебраических выражений, по которым можно судить об устойчивости САУ) и частотные (основаны на исследовании частотных характеристик).

8.2. Алгебраические критерии устойчивости

8.2.1. Необходимое условие устойчивости

Характеристическое уравнение системы с помощью теоремы Виета может быть записано в виде

D(p) = a o p n + a 1 p n-1 + a 2 p n-2 + . + a _n = a o (p-p ₁ )(p-p ₂ ). (p-p _n ) = 0,

где p ₁ , p ₂ , . p _n — корни этого уравнения. Если система устойчива, значит все корни левые, то есть вещественные части всех корней

отрицательны, что можно записать как a _i = -|a _i | . Подставим их в уравнение:

a ₀ (p + |a 1 |)(p + |a 2 | — j2)(p + |a 2 | + j2). = 0.

Перемножая комплексно сопряженные выражения, получим:

a ₀ (p + |a 1 |)((p + |a 2 |)2 + (2)2). = 0.

После раскрытия скобок должно получиться выражение

a ₀ p n + a 1 p n-1 + a 2 p n-2 + . + a n = 0.

Так как в скобках нет ни одного отрицательного числа, то ни один из коэффициентов a ₀ ,a 1 . a n не будет отрицательным. Поэтому необходимым условием устойчивости САУ является положительность всех коэффициентов характеристического уравнения: a ₀ > 0, a 1 > 0, . , a n > 0 . В дальнейшем будем рассматривать только уравнения, где a ₀ > 0 . В противном случае уравнение домножается на -1.

Рассмотренное условие является необходиным, но не достаточным условием. Необходимые и достаточные условия дают алгебраические критерии Рауса и Гурвица.

8.2.1. Критерий Рауса

Раус предложил критерий устойчивости САУ в виде алгоритма, по которому заполняется специальная таблица с использованием коэффициентов характеристического уравнения:

1) в первой строке записываются коэффициенты уравнения с четными индексами в порядке их возрастания;

2) во второй строке — с нечетными;

3) остальные элементы таблицы определяется по формуле: c _k,i = c _{k+ 1,i — 2} — ric _{k + 1,i — 1} , где ri = c _{1,i — 2} /c _{1,i — 1} , i 3 — номер строки, k — номер столбца.

4) Число строк таблицы Рауса на единицу больше порядка характеристического уравнения.

Корневые критерии устойчивости

1) отрицательная вещественная часть

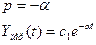
Устойчивая система.

2) положительные вещественные корни

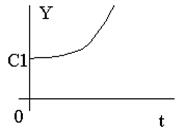
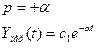
Неустойчивая система

3) корни комплексно-сопряженные с

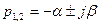
отрицательной вещественной частью

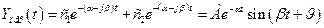
затухающие гармонические колебания

Система устойчива.

4) комплексно-сопряженные с положительной

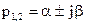
Неустойчивая система

5) комплексные корни (чисто мнимые)

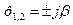
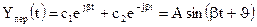монотонный колебательный процесс

с постоянной частотой и амплитудой.

Система на границе устойчивости.

Вывод:Чтобы САУ была устойчивой необходимо, чтобы вещественные части корней были отрицательными. Если хотя бы один корень имеет положительную вещественную часть, то процесс будет расходящийся а система – неустойчива.

Если корень равен 0, то малейшее появление отрицательной составляющей сделает процесс устойчиво колебательным, а положительной – неустойчиво колебательным.

Часто корни характеристического уравнения при анализе устойчивости систем изображают на комплексной плоскости – плоскости корней характеристического уравнения

Комплексная плоскость мнимой осью разбивается на 2 части. Левую сторону называют областью устойчивости,а правую – областью неустойчивого движения.

Если корни лежат на мнимой оси или в 0, то система находится на границе устойчивости.

Вывод:Для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения лежали слева от мнимой оси плоскости корней. Если хоть один корень справа, то система неустойчива. Таким образом, мнимая ось есть граница, за которую корни не должны переходить.

Если система имеет хотя бы один нулевой корень или хотя бы одну пару чисто мнимых корней, а все остальные корни имеют отрицательную вещественную часть, то система находится на границе устойчивости. При этом выделяют 3 типа границ устойчивости линейных систем:

1. Апериодическая граница устойчивости, которая соответствует р=0. Когда корень – нуль, то в характеристическом уравнении и система будет устойчива относительно скорости изменения управляемой величины, а сама управляющая величина может принимать произвольное значение. Система является нейтрально устойчивой.

2. Колебательная граница устойчивости, которой соответствуют чисто мнимые корни

В связи с тем, что корни характеристического уравнения определять трудно для систем высокого порядка, были разработан целый ряд критериев, с помощью которых судят об устойчивости систем.

Алгебраические критерии.

Критерий устойчивости Гурвица.

При рассмотрении алгебраических критериев используются лишь коэффициенты характеристического уравнения и необходимые и достаточные условия устойчивости систем.

Необходимое условие является справедливым для всех систем:

Все коэффициенты характеристического уравнения должны быть положительными

Необходимое условие является и достаточным для систем 1-го и 2-го порядка.

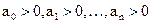
Для устойчивости линейной САУ по критерию Гурвица необходимо и достаточно, чтобы были положительными n главных определителей матрицы коэффициентов характеристического уравнения заданной системы (знаменатель передаточной функции):

Матрица коэффициентов

По диагонали от левого верхнего угла до правого нижнего выписывают все коэффициенты по порядку от а₁ до аn. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с чётными и нечётными индексами. В случае отсутствия даннного коэффициента или если его индекс n, то на его место пишется 0.

а1 а3 а5 ………0 1=а1>0

а0 а2 а4 ………0 а1 а3

0 а1 а3 а5…. 0 2= а0 а2

………………. а1 а3 а5

…………………

Если аn=0 , то имеет место апериодическая граница устойчивости.

Если n₁=0, то это колебательная граница устойчивости.

Критерий Раусса.

Так же базируется на коэффициентах характеристического уравнения, из которого строится таблица.

Для устойчивости систем по критерию Раусса необходимо и достаточно чтобы при а0>0 все коэффициенты первого столбца таблицы Раусса были положительными.

Для устойчивости системы все коэффициенты 1-го столбца должны быть больше 0

Частотные критерии

Критерий Михайлова.

Критерий базируется на поведении кривой, которую описывает конец вектора (X(ω),Y(ω)) замкнутой системы при изменении частоты от 0 до + .

Возьмём характеристический полином следующего вида:

(1)

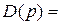
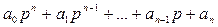
Подставим в него и выделим вещественную и мнимую части.

— вещественная часть,

— мнимая часть.

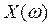
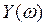
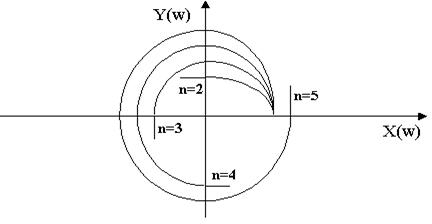
Изобразим годограф Михайловавыражения на комплексной плоскости.

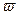
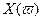
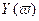
Берём значения и строим годограф. Для различных годограф имеет формы, представленные на рисунке. Эти годографы называются кривыми Михайлова.Кривая Михайлова строится по точкам, рассчитывается и для данной частоты, на кривой указываются значения частоты.

Формулировка критерия Михайлова.

Чтобы САР была устойчивой, необходимо и достаточно, чтобы вектор D(jω) при изменении частоты от 0 до +∞ начал движение с точки, лежащей на положительной вещественной оси, и, вращаясь только против часовой стрелки и нигде не обращаясь в нуль, прошел последовательно n квадрантов комплексной плоскости, повернувшись на угол n∙π/2, где n – степень характеристического уравнения D(jω)=0

Другими словами, требуется, чтобы кривая Михайлова проходила последовательно квадрантов против часовой стрелки, всё время огибая начало координат и уходила в в том квадранте, номер которого соответствует показателю степени полинома. Если это условие не выполняется, то система является неустойчивой.

Устойчивая Неустойчивая Апериодическая Колебательная

граница устойчивости граница устойчивости

Другая формулировка критерия Михайлова:

Она состоит в использовании свойства перемежаемости корней многочленов 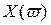и .

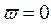
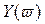
Идя по кривой Михайлова от т. в направлении возрастания частоты, мы выходим из оси , затем пересекаем ось , потом снова и т. д.

Это значит, что корни уравнений и должны следовать поочерёдно друг за другом.

Кривые и имеют приблизительно такой вид:

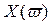
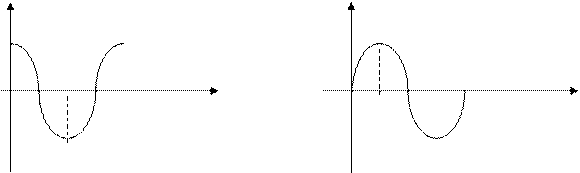
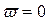
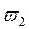
Перемежаться должны корни , , ,… Между ними должно быть следующее соотношение:

Условием устойчивости системы является перемежаемость корней полиномов вещественной и мнимой частей комплексной передаточной функции. Нарушение этого условия говорит о неустойчивости системы.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.).

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте: