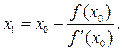Метод Ньютона
Инструкция . Введите выражение F(x) , нажмите Далее . Полученное решение сохраняется в файле Word . Также создается шаблон решения в Excel .
- Решение онлайн
- Видеоинструкция
- Оформление Word
Правила ввода функции, заданной в явном виде
- Примеры правильного написания F(x) :
- 10•x•e 2x = 10*x*exp(2*x)
- x•e -x +cos(3x) = x*exp(-x)+cos(3*x)
- x 3 -x 2 +3 = x^3-x^2+3
- Выражение 0.9*x=sin(x)+1 необходимо преобразовать к виду: sin(x)+1-0.9*x . Аналогично, x^2-7=5-3x к виду x^2+3x-12 .
Пусть дано уравнение f(x)=0 , где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b . Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x) . Число ξ называется корнем k -ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f k-1 (ξ) = 0 . Однократный корень называется простым.
Приближенное нахождение корней уравнения складывается из двух этапов:- Отделение корней, то есть установление интервалов [αi,βi] , в которых содержится один корень уравнения.
- f(a)•f(b) , т.е. значения функции на его концах имеют противоположные знаки.
- f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке).
- f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз.
- Уточнение приближенных корней, то есть доведение их до заданной точности.
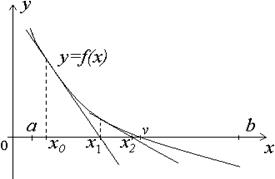
Геометрическая интерпретация метода Ньютона (метод касательных)
Критерий завершения итерационного процесса имеет вид
Метод Ньютона
Этот онлайн калькулятор ищет корень (нуль) заданной функции, используя метод Ньютона (также известный как метод касательных)
Этот онлайн калькулятор применяет метод Ньютона (также известный как метод касательных) используя калькулятор производных для получения аналитической формулы производной заданной функции (метод Ньютона требует вычисления производной). Под калькулятором можно прочитать краткое описание метода.
Метод Ньютона
Метод Ньютона 1
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации.
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. Далее процесс повторяется, пока не будет достигнута необходимая точность.
Уравнение касательной к графику функции выглядит следующим образом:
,
где — тангенс угла пересечения касательной с осью абсцисс.Тангенс угла пересечения касательной с осью абсцисс, — не что иное, как значение производной в точке .
С учетом того факта, что в точке пересечения с осью абсцисс значение y равно нулю, можно записать следующее выражение для нахождения точки пересечения (следующей точки приближения):Метод Ньютона является очень мощным методом поиска корней функции, так как имеет квадратичную скорость сходимости — количество значащих цифр примерно удваивается с каждым шагом итерации, однако существуют и ограничения, затрудняющие его применение. Так, например, если начальное приближение недостаточно близко к решению, то метод может не сойтись, если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня, если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена, если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Теорема Канторовича дает следующие условия применимости метода для поиска корней функции:
- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная f'(x) равномерно отделена от нуля;
- её вторая производная f»(x) должна быть равномерно ограничена.
Уточнение корней методом касательных (метод Ньютона)
Метод касательных, связанный с именем Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень v на отрезке [a,b], дифференцируема на этом отрезке, и её производная f’(x) не обращается на нем в нуль.
Возьмём произвольную точку x0 отрезка [a,b] и запишем в ней уравнение касательной к графику функции f(x):
Полагая в этом уравнении y=0, находим абсциссу x1 точки пересечения касательной с осью Ox:
Повторим проделанную процедуру: напишем уравнение касательной к графику функции y=f(x) при x=x1 и найдём для неё точку пересечения x2 с осью Ох:
Продолжая этот процесс, получим последовательность <xn>, определенную с помощью рекуррентной формулы
( 6) Процесс вычисления продолжается до тех пор, пока не будет выполнено условие: |xn+1 — xn| * взять x * = xn+1. Реализация алгоритма метода касательных представлена на блок-схеме в прил. 3.
Геометрически с помощью этого метода предлагаем построить касательную к кривой y=f(x) в выбранной точке x=xn, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню (рис.9).
Рис. 9. Геометрическая иллюстрация метода касательных (метода Ньютона)
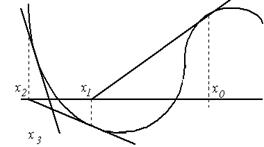
Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий и при их нарушении либо дает расходящийся процесс (рис.10), либо приводит к другому корню (рис.11).
Рис. 10. Расходящийся процесс Рис. 11. Приближение к другому корню
Теорема (о сходимости метода касательных). Пусть функция f(x) дважды непрерывно дифференцируема на [a,b], причем её производные удовлетворяют неравенствам
Предположим, что корень x=v уравнения (1) является внутренней точкой отрезка [a,b], т.е. a
Обычно, на практике, за начальное приближение x0 принимается такое значение из отрезка [a,b], для которого выполняется следующее условие:
f(x0) f ’’(x)>0. ( 7) Чаще всего выбирают х0=a или x0=b в зависимости от того, для какой из этих точек выполняется условие (7).
Метод Ньютона эффективен для решения тех уравнений, для которых значение модуля производной |f’(x)| близ корня достаточно велико, т.е. график функции y=f(x) в окрестностях данного корня имеет большую крутизну.
Метод Ньютона является наиболее быстрым среди численных методов вычисления корня функционального уравнения. На практике необходимая точность достигается буквально после выполнения нескольких (не более 10) итераций.
2.4. Уточнение корней методом простой итерации
Если каким-либо способом получено приближенное значение x0 корня уравнения (1), то уточнение корня можно осуществить методом простых итераций. Для этого уравнение (1) представляют в виде
x=j(x). ( 8) Возьмём произвольное значение x0 из области определения функции j(x) и будем строить последовательность чисел <xn>:
xn+1=j( xn), n=0,1,2,… ( 9) Для формулировки условий сходимости итерационной последовательности (9) нам нужно вспомнить один результат из математического анализа (формула конечных приращений Лагранжа). Предположим, что функция j(x) дифференцируема на [a,b]. При сделанных предположениях о дифференцируемости справедлива следующая формула, называемая формулой конечных приращений Лагранжа (см. [5], теорема 15, с.29)
Используя эту формулу, существование корня уравнения (8) можно установить с помощью предварительного исследования (8) с применением такого факта
Теорема (о сходимости метода простой итерации).Пусть x=v – корень уравнения (8) и пусть функция j(x) имеет в окрестности корня [v-d, v+d], d>0, производную j’(x), удовлетворяющую условию
источники:http://planetcalc.ru/7748/
http://megalektsii.ru/s56730t3.html