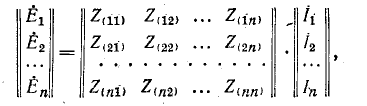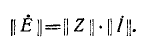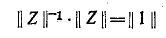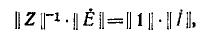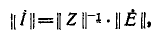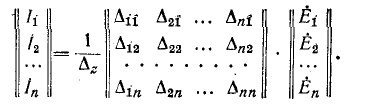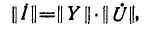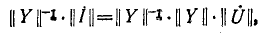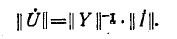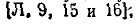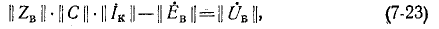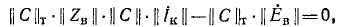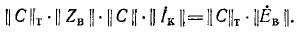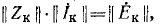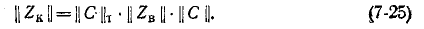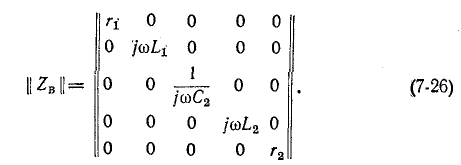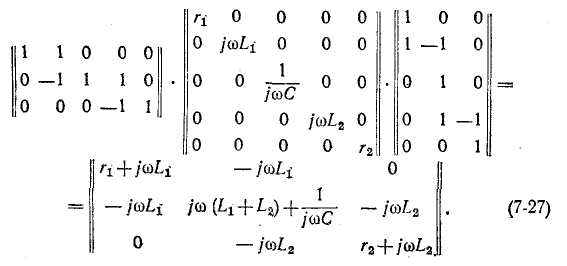Узловые уравнения в матричной форме
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Пусть имеем схему по рис. 1, где 
 . . | (1) |
Однако, для дальнейших выкладок будет удобнее представить ток 
 . . | (2) |
Подставив (2) в (1), получим:
 . . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
 , , | (4) |
где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , , | (5) |
 , , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с введенным ранее понятием матрицы главных контуров В , записываемой для главных контуров, в качестве независимых переменных примем токи ветвей связи, которые и будут равны искомым контурным токам.
Уравнения с контурными токами получаются на основании второго закона Кирхгофа; их число равно числу независимых уравнений, составляемых для контуров, т.е. числу ветвей связи c = n — m +1 . Выражение (6) запишем следующим образом:
 . . | (7) |
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
 , , | (8) |
где 

С учетом (8) соотношение (7) можно записать, как:
 | (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
 , , | (10) |
 . . | (11) |
то получим матричную форму записи уравнений, составленных по методу контурных токов:
 , , | (12) |
где 

В развернутой форме (12) можно записать, как:
 , , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZB T

Матрицы ЭДС и токов источников
 |  |
 |  |
Тогда матрица контурных ЭДС

Матрица контурных токов
 |  . . |
Таким образом, окончательно получаем:

где 








Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
 , , | (14) |
где 

Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
 , , | (15) |
 .. .. | (16) |
Выражение (16) перепишем, как:
 . . | (17) |
Принимая потенциал узла, для которого отсутствует строка в матрице А , равным нулю, определим напряжения на зажимах ветвей:
 . . | (18) |
Тогда получаем матричное уравнение вида:
 . . | (19) |
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
 | (20) |
 , , | (21) |
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 | (22) |
где 

В развернутом виде соотношение (22) можно записать, как:
 | (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
Данная схема имеет 3 узла ( m =3) и 5 ветвей ( n =5) . Граф схемы с выбранной ориентацией ветвей представлен на рис. 5.
А
Диагональная матрица проводимостей ветвей:
Y
где 
Матрица узловых проводимостей

Матрицы токов и ЭДС источников
 |  |
 |  |
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:

где 




Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем заключаются преимущества использования матричных методов расчета цепей?
- Запишите выражения матрицы контурных сопротивлений и матрицы контурных ЭДС.
- Запишите выражения матрицы узловых проводимостей и матрицы узловых токов.
- Составить узловые уравнения для цепи на рис. 2.
Составить контурные уравнения для цепи рис. 4, приняв, что дерево образовано ветвями 3 и 4 (см. рис. 5).
Метод узловых потенциалов
Метод узловых потенциалов (МУП), описанный здесь и здесь, излагается классическим (традиционным) способом, который, на мой взгляд, не раскрывает всей красоты метода, не говоря уже о том, что он не позволяет учитывать наличие взаимной индукции между ветвями и др. Ниже будет показан матрично-топологический способ вывода уравнений МУП, который позволяет не только учитывать наличие взаимной индукции между ветвями, но и делает вывод уравнений более наглядным и понятным. Кроме того, будет дан ряд замечаний к МУП, которые вскроют глубинную суть метода и откроют путь к другим замечательным методам расчета электрических цепей: методу узловых напряжений (МУН) и методам расчета «ортогональных» цепей (или, более правильно, «биортогональным»), о которых уже шла речь в статье.
Начнем с описания алгоритма расчета цепей методом узловых потенциалов.
Алгоритм расчета цепи методом МУП
1. Записываются уравнения по первому закону Кирхгофа для всех независимых узлов, т.е. для всех узлов, кроме базисного, или для (nу – 1) узлов:
где $ \bold
mi,j = +1 – если ток j-ой ветви входит в i-ый узел;
mi,j = -1 – если ток j-ой ветви выходит из i-го узла;
$ \bold<\Im_
$ \bold<_> $ – вектор токов ветвей схемы (искомый вектор);
$ \bold<\Im_> $ – вектор ИТ ветвей; причем $ \Im_
В качестве базисного узла может быть выбран любой узел цепи (обычно, в учебниках ТОЭ, в качестве базисного узла принимают узел земли, но на практике оказывается, что в некоторых случаях целесообразно выбирать и другие узлы).
2. Для каждой ветви составляются уравнения по закону Ома:
где $ \bold<
и подставляются в уравнение (1):
3. Напряжения ветвей $ \bold<_> $ выражаются через разности потенциалов независимых узлов схемы $ \boldsymbol<\varphi_
где $ \bold<
$ \varphi_<\textrm<б>> $ – потенциал балансирующего узла, который может быть принят любому наперёд заданному значению (балансирующий узел – это произвольный узел, который может даже не принадлежать рассматриваемой схеме).
Примечание. Действительно, поскольку i-ая строка матрицы $ \bold<
В МУП балансирующий узел выбирают так, чтобы он совпадал с базисным, что соответствует симметричной матрице узловых проводимостей, а его значение обычно принимается равным нулю $ \varphi_<\textrm<б>> = 0 $, при этом уравнение (4) примет вид
4. Записывают узловые уравнения. Для этого формула (5) подставляется в формулу (3):
и после небольших преобразований получаются узловые уравнения
где $ \bold<
$ \boldsymbol<\varphi_
$ \bold<
5. Узловое уравнение решается любым известным способом, например, матричным
и определяются токи ветвей по формуле (2) или с учетом (5):
Некоторые замечания к МУП
- В МУП схемы с особыми ветвями по сути не рассматриваются – такие схемы преобразуются в схемы без особых ветвей (ЭДС особых ветвей переносят через узел, узлы особой ветви «стягивают» в один узел), т.е. при записи уравнений (1) по первому закону Кирхгофа составляется nу – 1 – ne (для схемы с особыми ветвями) или nу – 1 уравнений (для схемы без особых ветвей).
- В некоторых учебниках ТОЭ [1], [2] при формулировке первого закона Кирхгофа токи, направленные к узлу, учитываются со знаком «-», от узла со знаком «+», в других [3] наоборот – токи, направленные к узлу принимаются со знаком «+», от узла со знаком «-». Поскольку принципиальной разницы нет (хотя более правилен первый способ), я буду придерживаться второго (более естественного и удобного для запоминания) правила.
- Понятно, что в схеме с особыми ветвями взятие обратной матрицы $ \bold<
_ > $ в уравнении (2) было бы невозможно, поэтому в МУП и МУН используют разные преобразования схемы: «стягивают узлы», переносят ЭДС через узел и т.д., но существует способ, который позволяет обойтись без переноса, стягивания и т.д. Этот способ рассматривается в теории «ортогональных» цепей, встречающихся в тензорном анализе сетей, но это тема отдельной публикации. - В учебниках ТОЭ матрица $ \bold
$ обычно обозначается через $ \bold $. - Кроме того, в учебниках ТОЭ в уравнении (1) вектор источников тока узлов не учитывается. Причина в том, что в учебниках предполагается, что источники тока узловых пар преобразованы в источники тока ветвей. Мы же рассматриваем более общий случай (на самом деле существует еще более общий случай, который опять же рассматривается в теории «ортогональных» цепей).
- Внимательный читатель, наверное, заметил, что в учебниках ТОЭ уравнение (4) не записывается (вместо него используется уравнение (5)). Я записал его здесь намеренно – для общности, чтобы показать, что в общем случае (на самом деле существует более общая форма записи уравнения (4), но она здесь не рассматривается) должна рассматриваться связь между напряжениями ветвей и узловыми напряжениями (ведь разность потенциалов узлов это и есть узловое напряжение). Действительно, в тех же учебниках ТОЭ один из потенциалов принимается равным нулю условно, а что будет если φб ≠ 0, кроме того даже если мы его и приняли равным нулю, это ведь не говорит о том, что его нет, не так ли?!
- Следует отметить, что в учебниках ТОЭ [1] в классической записи МУП напряжения ветвей обычно не выражаются через потенциалы узлов (хотя в матрично-топологической записи уравнение (5) отмечается): узловые уравнения получаются после подстановки уравнений для токов ветвей (2) в уравнения, составленные по первому закону Кирхгофа (1) и группировки слагаемых. Выражая напряжения ветвей через потенциалы узлов в матричном виде при выводе узловых уравнений, мы делаем вывод более наглядным и понятным.
- Записывая уравнения в матричном виде мы можем легко заметить, как учитывается взаимная индукция между ветвями схемы при расчете электрической цепи (она влияет как на матрицу узловых проводимостей, так и на вектор задающих токов узлов), чего нельзя сказать о классическом (традиционном) выводе МУП, где взаимная индукция не учитывается.
Пример
Найдем узловые напряжения и токи ветвей электрической цепи, схема замещения которой приведена на рисунке 1, а её граф на рисунке 2
Дано:
Примечание:
* – векторы $ \bold
** – числовые значения ЭДС, ИТ и сопротивлений приняты условно, без привязки к реальным параметрам элементов
*** – узлы будем обозначать символом «o», ветви – символом «b»
Решение:
В качестве базисного и балансирующего узла примем узел 5.
1. В соответствии с первым законом Кирхгофа
составим матрицу соединения ветвей в узлы $ \bold
2. Найдем матрицу проводимости ветвей
3. Составим узловые уравнения (найдём матрицу узловых проводимостей $ \bold
4. Найдем неизвестные потенциалы (напряжения) узлов $ \boldsymbol<\varphi_
Проверкой убеждаемся, что $ \bold
Несложно оценить простоту с которой были получены решения (решение классическим способом, из-за наличия взаимоиндукции, вызвало бы большие затруднения и несмотря на большое количество таблиц заняло бы гораздо больше места).
Литература
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. 1975.
- Демирчян К.С., Нейман Л.Р. и др. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 1. 4-е изд. Питер, 2004 г.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для Вузов. – М.: Высшая школа, 1984. – 559 с.
- Шимони К. Теоретическая электротехника. Издательство «Мир». Москва 1964 г. – 775 с.
Рекомендуемые записи
В программе онлайн-расчёта электрических цепей появился расчёт по методу узловых потенциалов. Выбор метода расчёта осуществляется в…
Наряду с решением электрических схем по законам Кирхгофа и методом контурных токов используется метод узловых…
В дополнение к выводу метода рассмотрим методику расчёта электрических цепей по методу узловых потенциалов. Последовательность…
Применение матриц к расчету электрических цепей
Применение матриц к расчету электрических цепей:
Математическая символика и правила матричной алгебры позволяют упростить запись систем уравнений, получающихся при расчете сложных электрических цепей. В этом отношении матричную алгебру можно сравнить со стенографией, которая облегчает и ускоряет запись.
Напомним, что матрица представляет собой совокупность величин, называемых ее элементами и расположенных в виде прямоугольной таблицы 1. Если число строк равно числу столбцов, то матрица называется квадратной. Матрица, содержащая один столбец, называется столбцовой или матрицей-столбцом.
Приведенная система уравнений, записанных по второму закону Кирхгофа для контурных э. д. с. и контурных токов, может быть представлена в виде произведений квадратной матрицы собственных и общих сопротивлений контуров на столбцовую матрицу контурных токов.
При этом следует помнить, что произведением двух матриц называется матрица, элементы которой равны сумме произведений всех элементов соответствующей строки первой матрицы на соответствующие элементы столбца второй матрицы. Итак, уравнения (7-2) в матричной форме имеют вид:
Данное матричное уравнение может быть решено относительно матрицы 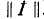
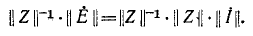
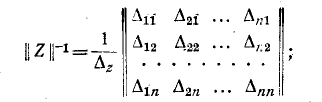
Как известно, для получения обратной матрицы необходимо заменить в исходной матрице-каждый элемент его алгебраическим дополнением, затем заменить строки соответствующими столбцами 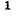
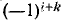
здесь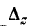
Произведение обратной матрицы на исходную матрицу равно единичной матрице, т. е. квадратной матрице, у которой все элементы главной диагонали (идущей от левого верхнего угла к правому нижнему) равны единице, а остальные элементы равны нулю.
где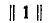
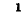
Произведение единичной матрицы на матрицу 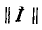
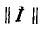
или в развернутой форме
В результате умножения матриц получаются выражения для контурных токов вида (7-4).
Аналогично решается матричное уравнение для узловых напряжений
где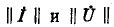
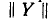
В результате умножения матрицы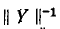
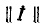
Матричная алгебра широко применяется для расчета сложных четырехполюсников.
В случае относительно простой электрической схемы без взаимной индукции матрица контурных сопротивлений легко записывается непосредственно по заданной схеме. В более сложных случаях матрица контурных сопротивлений может быть получена с помощью матрицы сопротивлений ветвей. Ниже показана связь, существующая между матрицами контурных сопротивлений и сопротивлений ветвей 
•Обозначим токи, напряжения, э. д. с. и сопротивления ветвей индексом «в», а соответствующие контурные величины — индексом «к». Связь между токами в ветвях и контурными токами выражается зависимостью
Здесь 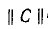
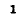
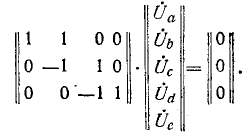
Например, для схемы рис. 7-25 имеем:
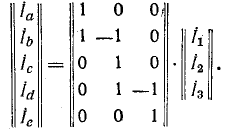
Уравнения вида (М2) по второму закону Кирхгофа в матричной форме записываются так:
где 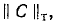
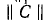
Строка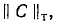
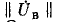
любом контуре равна нулю, т. е. «произведение» любой строки 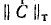
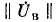
Например, для схемы рис, 7-25 имеем:
Считая, что направления э. д. с. и токов в ветвях совпадают, получаем матрицу напряжений на ветвях в виде
Подстановка (7-20) и (7-22) дает:
а подстановкой (7-23) в (7-21) получаем:
Сопоставив это уравнение с уравнением для контурных токов
приходим к выводу, что э. д. с. в ветвях и контурные э. д. с. связаны матричным уравнением
а матрица контурных сопротивлений получается по формуле
Для схемы рис. 7-25 матрица сопротивлений ветвей записывается в виде
Матрица контурных сопротивлений согласно (7-25) равна:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Дуальные цепи
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Теорема обратимости (или взаимности)
- Теорема компенсации
- Теорема об изменении токов в электрической цепи при изменении сопротивления в одной ветви
- Теорема об эквивалентном источнике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://faultan.ru/simulation/toe/node_voltages_matrix/
http://www.evkova.org/primenenie-matrits-k-raschetu-elektricheskih-tsepej