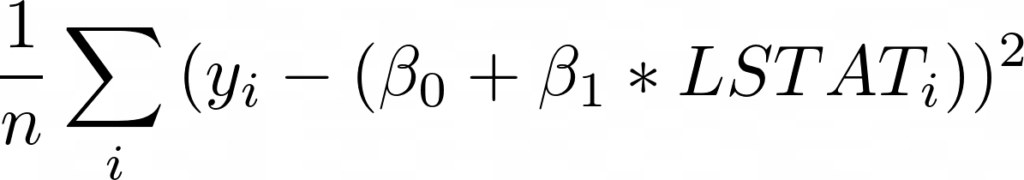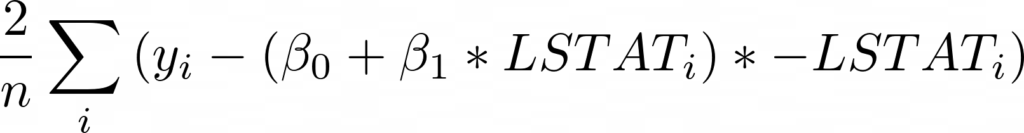Узнать уравнение регрессии в python

Полное руководство по линейной регрессии в Scikit-Learn

Обсудим модель линейной регрессии, используемую в машинном обучении. Используем ML-техники для изучения взаимосвязи между набором известных показателей и тем, что мы надеемся предсказать. Давайте рассмотрим выбранные для примера данные, чтобы конкретизировать эту идею.

В бой. Импортируем рабочие библиотеки и датасет:

Вот краткое описание нашего датасета:

• CRIM — уровень преступности на душу населения по городам.
• ZN — доля земли под жилую застройку, разделенная на участки площадью более 25 000 кв. футов.
• INDUS — доля акров, которые принадлежат предприятиям, не связанным с розничной торговлей, на город.
• CHAS — фиктивная переменная реки Чарльз (1, если участок соединен с рекой; 0 в противном случае).
• NOX — концентрация оксидов азота (в десятимиллионных долях).
• RM — среднее количество комнат в доме.
• AGE — доля занимаемых зданий, построенных до 1940 г.
• DIS — взвешенные расстояния до пяти бостонских центров занятости.
• RAD — индекс доступности радиальных автомобильных дорог.
• TAX — полная ставка налога на имущество за каждые 10000 долларов стоимости.
• PTRATIO — соотношение учеников и учителей по городам.
• B — 1000 (Bk — 0,63) , где Bk — доля граждан афроамериканского происхождения по городам.
• LSTAT — процент более низкого статуса населения.
• TARGET —медианное значение стоимости занимаемых домов в тысячах долларов США.

Задача данной выборки сводится к прогнозированию целевого показателя (медианной стоимости недвижимости), используя приведенные выше показатели (все, кроме TARGET).

Линейная регрессия

Как мы можем подойти к этой проблеме?
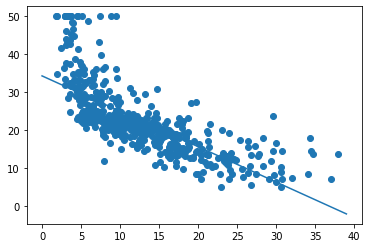
Для нашего первого прохода давайте упростим задачу. Допустим, мы просто хотим использовать признак LSAT для прогнозирования TARGET.

По оси X у нас есть LSTAT, а по оси Y — TARGET. Просто взглянув на это, можно увидеть отрицательную взаимосвязь: когда LSTAT растет, TARGET падает.

Функция оценки/стоимости

Как мы можем решить проблему предсказания TARGET на основе LSTAT? Хорошая отправная точка для размышлений: допустим, мы разрабатываем множество моделей для прогнозирования целевого показателя, как нам выбрать лучшую из них? Как только мы найдем подходящее для сравнения значение, наша задача — минимизировать/максимизировать его.

Это чрезвычайно полезно, если вы можете свести проблему к единственной оценочной метрике. Тогда это очень упрощает цикл разработки модели. Однако в реальном мире прийти к такому упрощению может быть непросто. Иногда не совсем понятно, что вы хотите, чтобы ваша модель максимизировала/минимизировала. Но это проблема для другой статьи.

Поэтому для нашей задачи предлагаю использовать среднюю квадратическую ошибку (mean squared error) в качестве оценочной метрики. Для лучшего понимания смысла MSE, давайте определимся с терминологией:

Таким образом, MSE:

По сути, для каждой точки мы вычитаем предсказанное нами значение из фактического. Затем, поскольку нас не волнует направление ошибки, мы возводим разницу в квадрат. Наконец, мы вычисляем среднее всех этих значений. Таким образом, мы хотим, чтобы среднее расстояние между предсказанными и фактическими показателями было минимальным.

Вам может быть интересно, почему мы возводили разницу в квадрат вместо того, чтобы брать абсолютное значение. Оказывается, что для некоторых из представленных ниже математических операций возведение в квадрат работает лучше. Кроме того, это метод максимального правдоподобия. Тем не менее, такой подход приводит к тому, что крупные ошибки имеют более сильное влияние на среднее значение, поскольку мы возводим в квадрат каждое отклонение.

Наша модель

Теперь, когда у нас есть функция оценки, как найти способ ее минимизировать? В этом посте мы рассмотрим модель линейной регрессии. Она выглядит следующим образом:

Где j — количество имеющихся у нас предсказателей (независимых переменных), значения бета — это наши коэффициенты. А бета 0 является смещением (intercept). По сути, данная модель представляет собой линейную комбинацию наших предсказателей с intercept.

Теперь, когда у нас есть модель и функция оценки, наша задача состоит в том, чтобы найти бета-значения, которые минимизируют MSE для наших данных. Для линейной регрессии на самом деле существует решение в замкнутой форме, называемое нормальным уравнением. Однако в этом посте мы собираемся использовать другую технику — градиентный спуск.

Градиентный спуск

Градиентный спуск — это метод, который мы позаимствовали из оптимизации. Очень простой, но мощный алгоритм, который можно использовать для поиска минимума функции.

1. Выберите случайное начальное значение.
2. Делайте шаги, пропорциональные отрицательному градиенту в текущей точке.
3. Повторяйте, пока не достигните предела.

Этот метод найдет глобальный минимум, если функция выпуклая. В противном случае мы можем быть уверены только в том, что достигнем локальный минимум.

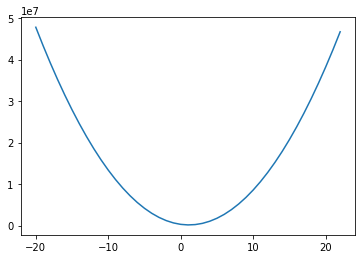
Первый вопрос, на который нам нужно ответить: является ли наша функция оценки выпуклой? Давайте посмотрим:

Для построения графика выше мы взяли диапазон значений коэффициентов для LSTAT, и для каждого из них рассчитали MSE на основе наших данных. Если мы затем отобразим полученные значения, мы получим приведенную выше кривую — выглядит довольно выпуклой! И оказывается, что наша функция MSE с нашей моделью линейной регрессии всегда будет выпуклой! Это означает: мы можем использовать градиентный спуск, чтобы найти оптимальные коэффициенты для нашей модели!

Одна из причин того, что градиентный спуск более распространен, чем нормальное уравнение для машинного обучения, заключается в том, что он намного лучше масштабируется по мере увеличения количества показателей. Это также стандартный метод оптимизации, который используется повсюду в машинном обучении. Поэтому понимание того, как он работает, чрезвычайно важно.

Градиенты

Если вы снова посмотрите на наш псевдокод для градиентного спуска, вы увидите, что на самом деле все, что нам нужно сделать, это вычислить градиенты. Итак, что такое градиенты? Это просто частные производные по коэффициентам. Для каждого имеющегося коэффициента нам нужно будет вычислить производную MSE по этому коэффициенту. Давайте начнем!

Для начала запишем выражение для MSE, подставив функцию оценки со смещением и единственной переменной LSTAT:

Теперь, взяв производную по бета 0, мы получим (умноженное на -1):

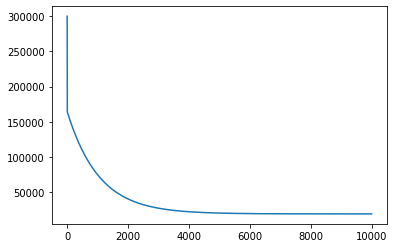
Теперь давайте запустим наш алгоритм градиентного спуска и убедимся, что MSE действительно уменьшается:

Первый график, представленный выше, показывает значение MSE, когда мы запускаем градиентный спуск. Как и следовало ожидать, MSE уменьшается со временем по мере выполнения алгоритма. Это означает, что мы постоянно приближаемся к оптимальному решению.

На графике видно, что мы вполне могли завершить работу раньше. MSE переходит в прямую (почти не изменяется) примерно после 4000 итераций.

Итак, запуск градиентного спуска показал, что оптимальное смещение составляет 34.55, а оптимальный наклон равен -0,95. На приведенном выше графике эта линия показана поверх наших данных, она выглядит как аппроксимирующая прямая.

Скорость обучения

Один параметр, который нам еще предстоит обсудить, — это скорость обучения. Эта скорость — гиперпараметр, используемый для определения того, насколько большие шаги мы делаем от направления градиента. Как узнать, какое значение выбрать? Как правило, можно попробовать множество вариантов. Вот некоторые из них, которые были предложены Andrew Ng: .001, .003, .01, .03, .1, .3, 1, 3.

Выбор слишком малого значения приводит к более медленной сходимости. Выбор слишком большого значения может привести к перешагиванию через минимум и расхождению.

Существуют также другие оптимизаторы градиентного спуска, которые более сложны и адаптируют скорость обучения за вас. Это также то, что вы можете делать самостоятельно, постепенно снижая скорость обучения.

Когда прекратить итерацию?

В моем коде я просто выполняю наш цикл 10000 раз. Почему 10000? Никакой реальной причины, кроме моей уверенности в том, что этого достаточно, чтобы достичь минимума. Такой подход точно нельзя назвать лучшей практикой. Вот несколько более разумных идей:

1. Следите за оценкой после каждого цикла, и когда ее очередное изменение меньше некоторого граничного значения — скажем, 0.001 — останавливайтесь.
2. Используйте проверочный датасет (validation set) и отслеживайте число ошибок, например, с помощью MSE. Когда метрика перестанет уменьшаться, остановитесь.

Нормализация данных

При работе с градиентным спуском вы хотите, чтобы все ваши данные были нормализованы. Вычтите среднее значение и разделите на стандартное отклонение для всех ваших тренировочных показателей. Обычно это ускоряет обучение и снижает вероятность застревания в локальном оптимуме, если функция оценки не является выпуклой.

Другие виды градиентного спуска

Показанный здесь градиентный спуск представляет собой классическую форму, что означает: каждое обновление коэффициента использует все данные для вычисления градиентов. Существует также стохастический градиентный спуск. Ему необходима только 1 строка данных (1 наблюдение) для пересчета коэффициентов в каждом цикле.

Такой способ намного лучше масштабируется, так как нужно обработать только одну строку данных за раз перед обновлением. Также он является более неопределенным, поскольку вы пытаетесь перемещаться с использованием градиента, рассчитанного на основе единственного наблюдения.

Другой тип градиентного спуска — это мини-пакетный градиентный спуск. Эта форма представляет собой компромисс между двумя, где вы выбираете размер пакета. Скажем, 32 (или, что еще лучше, пакетный график, который начинается с небольших пакетов и увеличивается с увеличением количества эпох), и каждая итерация вашего градиентного спуска использует 32 случайные строки данных для вычисления градиента (алгоритм воспользуется всеми строками перед повторной выборкой раннее обработанных). В результате мы получаем некоторую масштабируемость, но и некоторую неопределенность.

Такое случайное поведение оказывается полезным для функций оценки, которые не являются выпуклыми (глубокое обучение), поскольку оно может помочь модели избежать локального минимума. Это наиболее распространенный метод для невыпуклых функций оценки.

Допущения нашей модели

Всякий раз, когда вы имеете дело с моделью, хорошо знать, какие допущения она делает. Университет Дьюка написал об этом целую статью:

Реализация линейной регрессии в Scikit-Learn

Теперь, когда мы немного разбираемся в теории и реализации, давайте обратимся к библиотеке scikit-learn, чтобы на самом деле использовать линейную регрессию на наших данных. Написание моделей с нуля довольно полезно для обучения, но на практике вам, как правило, гораздо лучше использовать проверенную и широко используемую библиотеку.

Для начала нужно нормализовать данные:

У Scikit-learn довольно удобный API. Он предоставляет множество моделей, и все они имеют функции fit и predict . Вы можете вызвать fit с вашими X и y данными для обучения модели, а затем использовать predict для получения предсказанных значений на основе новых данных. Scikit-learn также предоставляет множество метрик, которые вы можете использовать для оценки, такие как MSE. Здесь я вычисляю среднеквадратическую ошибку (RMSE). Так мы можем использовать шкалу нашего целевого показателя, что, легче для понимания.

SGDRegressor выполняет линейную регрессию с использованием градиентного спуска и принимает следующие аргументы: tol (сообщает модели, когда следует прекратить итерацию) и eta0 (начальная скорость обучения).

RMSE в итоге составила 4.68… для нашей обучающей выборки с использованием scikit-learn.

Полиномиальные переменные

Рассматривая построенный выше график стоимости от LSTAT, вы могли заметить, что между данными показателями существует полиномиальная связь. Линейная регрессия хорошо подходит в случае линейной зависимости, но, если вы добавите полиномиальные показатели, такие как LSTAT, вы сможете установить более сложные отношения. SKLearn упрощает данный процесс:

Функция PolynomialFeatures сгенерировала новую матрицу показателей, состоящую из всех их полиномиальных комбинаций со степенью меньше или равной указанной (в нашем примере 2). Затем мы нормализовали эти данные и скормили их нашей модели. Так мы получили улучшенную тренировочную RMSE, равную 3.24. Однако обратите внимание, что эти результаты, представленные в иллюстративных целях, используют только тренировочную выборку.

Категориальные переменные

Линейная регрессия — одна из моделей, с которой нужно быть осторожным, когда у вас есть качественные данные. Если у вас переменные со значениями 1, 2 и 3, которые на самом деле означают «Мужской», «Женский», «Нет ответа», не передавайте их модели таким образом, даже если они являются числами.

Если бы вы это сделали, модель присвоила бы такому показателю коэффициент — возможно, 0.1. Это будет означать, что принадлежность к женскому полу увеличивает предсказанное значение на 0.1. А отсутствие ответа — на 0.2. Но, возможно, метка «Женский» должна повысить результат на 1.2, а «Нет ответа» — всего на 0.001. Чтобы решить данную проблему, вы должны преобразовать такие значения в фиктивные переменные, чтобы каждая категория имела свой собственный вес. Вы можете узнать, как это сделать с помощью scikit-learn, здесь.

Интерпретация вашей модели

Линейная регрессия — это отличная статистическая модель, которая существует уже давно. Есть много статистических методов, которые можно использовать для ее оценки и интерпретации. Мы не будем рассматривать их все и на самом деле сосредоточимся на очень простых подходах, которые, возможно, более распространены в машинном обучении, чем в статистике.

Во-первых, давайте посмотрим на коэффициенты, которым научилась наша модель (по всем показателям):

Что они означают? Каждый коэффициент представляет собой среднее изменение цены на жилье при изменении соответствующего показателя на единицу с условием, что все остальные показатели остаются неизменными. Например, если значения других показателей не затрагиваются, то увеличение LSTAT на единицу снижает наш целевой показатель (цену на жилье) на 3.72, а увеличение RM увеличивает его на 2.85.

Таким образом, если вы хотите повысить стоимость дома, то может быть стоит начать с увеличения RM и уменьшения LSTAT. Я говорю «может быть», потому что линейная регрессия рассматривает корреляции. Судя по нашим данным, такая взаимосвязь имеет место быть, что само по себе не означает обязательное наличие причинно-следственной связи между показателями.

Доверительные интервалы

Часто в машинном обучении очень полезно иметь доверительный интервал вокруг ваших оценок. Есть разные способы сделать это, но одним довольно общим методом является использование bootstrap .

Bootstrap — это случайная выборка на основе наших данных, и эта выборка того же размера, что и исходные данные. Так мы можем создать несколько представлений одних и тех же данных. Давайте создадим 1000 bootstrap-семплов наших данных.

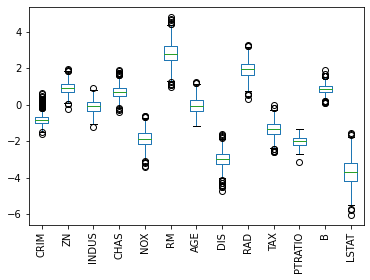
Затем мы обучим модель на каждом из полученных датасетов и получим следующие коэффициенты:

На представленной диаграмме размаха показан диапазон значений коэффициентов, которые мы получили для каждого показателя для всех моделей, которые мы обучили. AGE — особенно интересен, потому что значения коэффициентов были как положительными, так и отрицательными, что является хорошим признаком того, что, вероятно, нет никакой связи между возрастом и стоимостью.

Кроме того, мы можем увидеть, что LSTAT имеет большой разброс в значениях коэффициентов, в то время как PTRATIO имеет относительно небольшую дисперсию, что повышает доверие к нашей оценке этого коэффициента.

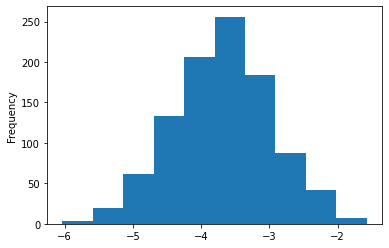
Мы даже можем немного углубиться в полученные коэффициенты для LSTAT:

Теперь мы можем с большой уверенностью сказать, что фактический коэффициент LSTAT отрицателен и почти наверняка находится между -2 и -5.5.

Разделение на обучающий/тестовый датасеты и кросс-валидация

До этого момента мы тренировались на всех имеющихся данных. Это может иметь смысл, потому что мы хотим максимизировать их полезность, используя как можно больше данных для обучения. С другой стороны, из-за такого подхода нам становится труднее оценивать, насколько хорошо работает наша модель. Причина этого в том, что, если мы продолжим рассчитывать MSE, используя тренировочные данные, мы можем обнаружить, что при применении модели на незнакомых ей данных, она работает довольно плохо.

Эта идея называется переобучением (overfitting). По сути, такая модель работает намного лучше с обучающими данными, чем с новыми. Она была чрезмерно натренирована на обнаружение уникальных характеристик обучающего множества, которые не являются общими закономерностями, присущими генеральной совокупности.

Другая сторона проблемы называется bias. Модель имеет высокий bias, когда она плохо обучена. В этом случае MSE будет высокой как для тренировочных данных, так и для данных, не показанных во время обучения.

В ML всегда существует компромисс между смещением (bias) и дисперсией (overfitting). По мере того, как ваши модели становятся более сложными, возрастает риск переобучения на тренировочных данных.

Теперь, когда мы знаем о проблемах с вычислением MSE, используя только обучающее множество, что мы можем сделать, чтобы лучше судить о способности модели к обобщению? А также диагностировать overfitting и bias? Типичным решением является разделение наших данных на две части: обучающий и тестовый датасеты.

Теперь, когда у нас есть два отдельных набора данных, мы можем тренировать модель на обучающем множестве и вычислять метрики, используя оба датасета (лучше всего использовать ваши тестовые данные после настройки модели):

Отлично! Теперь у нас есть MSE как для тренировочных данных, так и для данных тестирования. И оба значения довольно близки, что говорит об отсутствии проблемы с переобучением. Но достаточно ли они низкие? Большие значения предполагают наличие высокого bias.

Один из способов разобраться в этом — построить график обучения. Кривая обучения отображает нашу функцию ошибок (MSE) с различными объемами данных, используемых для тренировки. Вот наш график:

Вы можете видеть, что с менее чем 50 обучающими примерами тренировочная MSE неплохая, а кросс-валидация оставляет желать лучшего — довольно плохая (мы еще не говорили о кросс-валидации, так что пока думайте об этом как о тестировании). Если бы у нас было только такое количество данных, это выглядело бы как явная проблема высокой дисперсии (переобучения).

По мере увеличения наших данных мы начинаем улучшать оба результата, и они становятся очень похожими, что говорит о том, что у нас нет проблемы переобучения. Как правило, при высокой дисперсии на этом графике две линии будут находится довольно далеко друг от друга, и кажется, что, если мы продолжим добавлять больше данных, они могут сойтись.

Этот график больше похож на проблему с большим смещением (bias), поскольку две наши кривые очень близки и сглаживаются. Однако трудно сказать наверняка, потому что, возможно, мы только что достигли наилучшего возможного MSE. В таком случае это не будет проблемой высокого смещения. Такой результат был бы ей только в том случае, если бы наши кривые выровнялись при значении MSE выше оптимального. В реальной жизни вы не знаете, какова оптимальная MSE, поэтому вам нужно немного поразмышлять, считаете ли вы, что уменьшение bias улучшит ваш результат — но лучше просто попробуйте!

Устранение проблем высоких bias/variance

Итак, теперь, когда вы диагностировали проблему смещения или дисперсии, как ее исправить?

Для высокой дисперсии:

• Получите больше данных для обучения
• Попробуйте меньший набор показателей
• Используйте менее сложную модель
• Добавьте регуляризацию

Для высокого смещения:

• Попробуйте увеличить число показателей
• Перейдите на более сложную модель

Кросс-валидация и настройка гиперпараметров

Ранее мы упоминали этот термин: кросс-валидация. Давайте поговорим об этом сейчас. На данный момент мы узнали, что неплохо разделить данные на наборы для обучения и тестирования, чтобы лучше понять, насколько хорошо работает модель. Это замечательно, но представьте, что мы хотим протестировать несколько разных моделей или протестировать разные параметры нашей модели — например, другую скорость обучения или толерантность. Как бы нам решить, какая модель или какой параметр лучше? Будем ли мы обучать все на тренировочных данных и тестировать все на наших тестовых данных?

Надеюсь, вы понимаете, что это не имеет смысла, потому что тогда мы, по сути, оказались бы в том же месте, что и раньше, без возможности проверить, насколько хорошо мы справляемся с ранее неизвестными данными. Итак, мы хотим сохранить датасет для тестирования незапятнанным в том смысле, что в идеальном мире мы бы запускали наши тесты на нем только после того, как провели все необходимые эксперименты и были уверены в том, что нашли самую лучшую модель.

Похоже, нам нужен третий набор данных – датасет для валидации. По сути, мы можем разбить наши обучающие данные на две части: обучающий и проверочный датасеты. Все модели будут обучены на тренировочном множестве, а затем протестированы на нашем проверочном наборе. Затем мы выберем модель, которая лучше всего справляется с проверкой, и посмотрим, насколько удачно она пройдет тестирование. Результаты тестирования покажут, как хорошо наша модель будет работать с незнакомыми данными, и на этом мы завершим процесс разработки.

Примечание: в статье предполагается, что используемые тестовые и проверочные датасеты представляют собой репрезентативные выборки из нашей совокупности. Например, если средняя цена дома в вашем проверочном множестве составляет 1 миллион, а для генеральной совокупности соответствующее значение равно 300 тысячам, у вас плохая выборка. Часто мы случайным образом делим имеющиеся данные на три выборки, но всегда полезно подтвердить, что эти наборы являются репрезентативными. В противном случае вы обнаружите, что ваша модель, которая хорошо зарекомендовала себя при проверке и тестировании, плохо работает на реальных данных.

На практике вместо создания единого множества для проверки мы часто используем k-блочную кросс-валидацию.

Это означает, что мы выбираем значение k, скажем 3. Затем мы берем наши обучающие данные и делим их на 3 части. Мы случайным образом выбираем 2 блока для тренировки, а затем используем оставшийся для тестирования. Повторяем этот процесс еще 2 раза, так чтобы все наблюдения были использованы как для обучения, так и для проверки, и каждое из них применялось для валидации только один раз. После этого усредняем все три оценки (в нашем случае MSE), чтобы получить общую оценку для конкретной модели. Затем мы можем повторить этот процесс для других моделей, чтобы найти лучшую.

Вот видео, которое более наглядно описывает этот подход (с русскими субтитрами): https://www.youtube.com/watch?v=TIgfjmp-4BA

Этот процесс довольно просто реализуется с помощью sklearn:

Здесь мы фактически использовали рандомизированный поиск ( RandomizedSearchCV ), который обычно лучше, чем поиск по всем возможным значениям. Часто вы хотите попробовать много разных параметров для множества различных регуляторов, и сеточный поиск (перебор всех возможных комбинаций) вам не подходит.

Обычно вы хотите использовать рандомизированный поиск (случайный выбор комбинаций), как мы сделали выше. Хотя, поскольку у нас было только небольшое количество значений, мы заставили его работать как сеточный поиск, установив n_iter_search равным числу вариантов, которые мы хотели попробовать.

Мы также установили cv=3 , чтобы иметь 3 блока и использовали отрицательную MSE, потому что функции CV в scikit-learn пытаются максимизировать значение.

Вы можете узнать больше о случайном и «сеточном» вариантах поиска здесь: https://scikit-learn.org/stable/modules/grid_search.html.

Кроме того, в scikit-learn есть много других CV функций, которые полезны, особенно если вы хотите протестировать разные модели с одинаковыми блоками. Вот некоторая документация: https://scikit-learn.org/stable/modules/cross_validation.html.

Регуляризация

В качестве средства борьбы с высокой дисперсией я упомянул регуляризацию. Вы можете думать о ней как о методе, который используется для наказания модели за обучение сложным взаимосвязям. Для линейной регрессии она принимает форму трех популярных подходов. Все эти методы сосредоточены на идее ограничения того, насколько большими могут быть коэффициенты наших показателей.

Идея состоит в том, что если мы переоцениваем влияние предсказателя (большое значение коэффициента), то, вероятно, мы переобучаемся. Примечание: у нас все еще могут быть просто большие коэффициенты. Регуляризация говорит о том, что уменьшение MSE должно оправдывать увеличение значений коэффициентов.

• Регуляризация L1 (Lasso): вы добавляете сумму абсолютных значений коэффициентов к функции оценки. Этот метод может принудительно обнулить коэффициенты, что затем может быть средством выбора показателей.
• Регуляризация L2 (Ridge): вы добавляете сумму квадратов значений коэффициентов к функции оценки.
• Эластичная сетка: вы добавляете обе и выбираете, как их утяжелить.

Каждый из этих методов принимает весовой множитель, который говорит вам, насколько сильное влияние регуляризация будет иметь на функцию оценки. В scikit-learn такой параметр называется альфа. Альфа равный 0 не добавит штрафа, в то время как высокое его значение будет сильно наказывать модель за наличие больших коэффициентов. Вы можете использовать кросс-валидацию, чтобы найти хорошее значение для альфа.
Sklearn упрощает это:

Линейная регрессия на Python: объясняем на пальцах

Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!

Что такое регрессия?

Регрессия ищет отношения между переменными.

Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.

Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.

Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.

Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.

Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.

Зависимые данные называются зависимыми переменными, выходами или ответами.

Независимые данные называются независимыми переменными, входами или предсказателями.

Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.

Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.

Когда вам нужна регрессия?

Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.

Где она вообще нужна?

Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.

Линейная регрессия

Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.

Постановка проблемы

Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.

Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.

Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.

Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.

Простая линейная регрессия

Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.

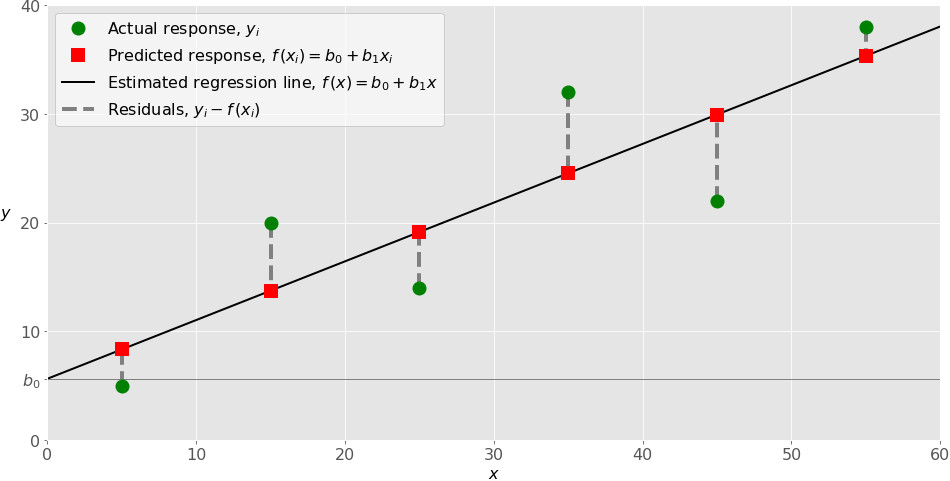
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.

Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.

Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).

Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.

Реализуйте линейную регрессию в Python

Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.

Пакеты Python для линейной регрессии

NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.

Незнакомы с NumPy? Начните с официального гайда.

Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.

Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.

Простая линейная регрессия со scikit-learn

Начнём с простейшего случая линейной регрессии.

Следуйте пяти шагам реализации линейной регрессии:

1. Импортируйте необходимые пакеты и классы.
2. Предоставьте данные для работы и преобразования.
3. Создайте модель регрессии и приспособьте к существующим данным.
4. Проверьте результаты совмещения и удовлетворительность модели.
5. Примените модель для прогнозов.

Это общие шаги для большинства подходов и реализаций регрессии.

Шаг 1: Импортируйте пакеты и классы

Первым шагом импортируем пакет NumPy и класс LinearRegression из sklearn.linear_model :

Теперь у вас есть весь функционал для реализации линейной регрессии.

Фундаментальный тип данных NumPy – это тип массива numpy.ndarray . Далее под массивом подразумеваются все экземпляры типа numpy.ndarray .

Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.

Шаг 2 : Предоставьте данные

Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray ) или похожими объектами. Вот простейший способ предоставления данных регрессии:

Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape() на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).

Вот как x и y выглядят теперь:

Шаг 3: Создайте модель

На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.

Давайте сделаем экземпляр класса LinearRegression , который представит модель регрессии:

Эта операция создаёт переменную model в качестве экземпляра LinearRegression . Вы можете предоставить несколько опциональных параметров классу LinearRegression :

• fit_intercept – логический ( True по умолчанию) параметр, который решает, вычислять отрезок b₀ ( True ) или рассматривать его как равный нулю ( False ).
• normalize – логический ( False по умолчанию) параметр, который решает, нормализовать входные переменные ( True ) или нет ( False ).
• copy_X – логический ( True по умолчанию) параметр, который решает, копировать ( True ) или перезаписывать входные переменные ( False ).
• n_jobs – целое или None (по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях. None означает отсутствие процессов, при -1 используются все доступные процессоры.

Наш пример использует состояния параметров по умолчанию.

Пришло время задействовать model . Сначала вызовите .fit() на model :

С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model . Поэтому можно заменить две последние операции на:

Эта операция короче и делает то же, что и две предыдущие.

Шаг 4: Получите результаты

После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.

Вы можете получить определения (R²) с помощью .score() , вызванной на model :

.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².

model содержит атрибуты .intercept_ , который представляет собой коэффициент, и b₀ с .coef_ , которые представляют b₁:

Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.

Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.

Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:

Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.

Шаг 5: Предскажите ответ

Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.

Получите предсказанный ответ, используя .predict() :

Применяя .predict() , вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.

Вот почти идентичный способ предсказать ответ:

В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.

Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.

Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1) , x.flatten() или x.ravel() при умножении с помощью model.coef_ .

На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:

Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new . Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.

О LinearRegression вы узнаете больше из официальной документации.

Теперь у вас есть своя модель линейной регрессии!

Python, корреляция и регрессия: часть 2

Предыдущий пост см. здесь.

Регрессия

Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.

Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.

Описываемые этими уравнениями линии называются линиями регрессии . Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.

Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.

Линейные уравнения

Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:

Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1.8. Подставив в наше уравнение значения a и b, получим:

Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:

Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:

Этот пример сгенерирует следующий ниже линейный график:

Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.

Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.

Остатки

К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:

Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:

Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).

Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.

Обычные наименьшие квадраты

Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.

Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.

Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:

Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:

Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:

Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.

Наклон и пересечение

Мы уже рассматривали функции covariance , variance и mean , которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:

В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1.6910.

Интерпретация

Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp , обратной для функции np.log . Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.

Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.

Визуализация

Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.

Функция regression_line возвращает функцию от x, которая вычисляет a + bx.

Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.

График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:

За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.

Допущения

Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.

Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.

Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.

Качество подгонки и R-квадрат

Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т.е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. Коэффициент детерминации R 2 , или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.

Обычно, чем ближе R 2 к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R 2 можно вычислить с помощью следующей ниже формулы:

Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т.е. дисперсией данных веса в популяции.

Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.

Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R 2 до единицы — это доля изменчивости, объясненная моделью.

Как и в случае с r , низкий R 2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.

Значение R 2 описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R 2 . По мере удаления либо приближения от своих оптимальных значений R 2 всегда будет расти.

Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R 2 путем деления дисперсии остатков на дисперсию значений y:

В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.

В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R 2 и коэффициентом корреляции r является прямолинейной:

Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R 2 составит 0.5 2 , т.е. 0.25.

Множественная линейная регрессия

Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.

Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:

Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β₁ = a и β₂ = b при условии, что x₁ всегда гарантированно равен 1, вследствие чего β₁ — это всегда константная составляющая, которая представляет наше пересечение, при этом x₁ называется (постоянным) смещением уравнения регрессии, или членом смещения.

Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:

Каждое значение от x₁ до x_n соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β₁ до β_n соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.

Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.

До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.

Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.

Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.