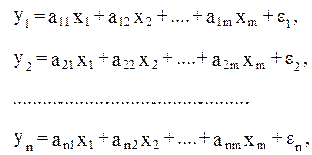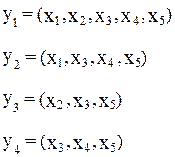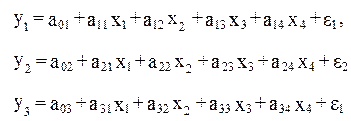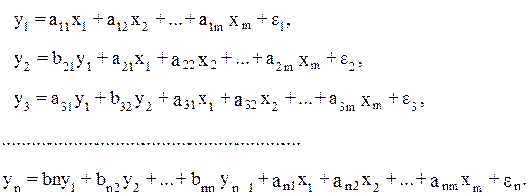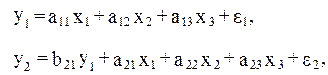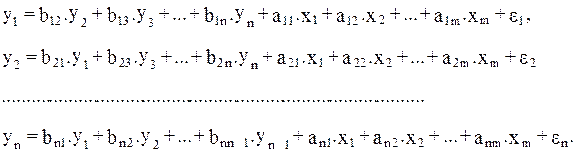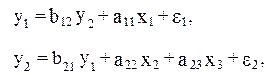Задание рекурсивных функций при помощи системы уравнений
В общем случаерекурсией называется такой способ задания функции, при котором значения определяемой функции для произвольных значений аргументов выражаются известным образом через значения определяемой функции для меньших значений аргументов.
Рассмотрим равенство f(х)=g(x), где f(х) и g(x) некоторые функции. Когда говорят, что это равенство есть уравнение, то это означает, что равенство рассматривается как неопределенное высказывание, при одних значениях х истинное, при других ложное.
Произвольная система рекурсивных уравнений задает частично – рекурсивную функцию. Если данная функция определена на всем множестве натуральных чисел, то она будетобщерекурсивной.Также верно другое утверждение.Функция является общерекурсивной, если она определена посредством ряда уравнений некоторого типа.
Затруднение вызвано тем, что просмотр набора уравнений обычно не убеждает нас в том, что эти уравнения “определяют” какую-либо функцию вообще. Когда говорится “функция”, обычно понимается под этим “правило, которое каждому значению (или набору из п значений, если мы имеем функцию n переменных) ставит в соответствие результирующее значение”. Но в общем случае система уравнений не всегда дает определенное значение.

задает некоторую функцию Ф(x). Однако ответить на вопрос, определяет ли данная система эту функцию Ф в общем случае невозможно. В данном конкретном случае такие выводы очевидно можно сделать на основе обычного подсчета значений и наших наблюдений касательно поведения функции при росте ее аргумента.
| x = | уравнение | f(x) | уравнение | Ф(x) |
| f(0)=3 | Ф(0)+0=3 | Ф(0)=3 | ||
| f(0+1)=f(0)+2=3+2=5 | f(1)=5 | Ф(1)+3*1=5 | Ф(1)=2 | |
| f(1+1)=f(1)+2=5+2=7 | f(2)=7 | Ф(2)+3*2=7 | Ф(2)=1 | |
| f(2+1)=f(2)+2=7+2=9 | f(3)=9 | Ф(3)+3*3=9 | Ф(3)=0 | |
| f(3+1)=f(3)+2=9+2=11 | f(4)=11 | Ф(4)+3*4=11 | Ф(4) не опред |
Из таблицы видно, что для значений x=4 и выше значение функции Ф не определено. Т.о. функция Ф(х) – частично-рекурсивная функция.
Т.о. вполне допустимой является ситуация, когда для некоторых (или даже для всех) точек значение функции не определено – считается, что в этих точках сама функция не определена. Это явление весьма характерно. Поэтому, делая предположение, что система уравнений действительно определяет общерекурсивную функцию, нужно всегда проявлять осторожность. Обычно требуется дополнительное доказательство этого положения, например, в виде индуктивного доказательства того, что для каждого значения аргумента вычисление завершается выдачей единственного значения.

задает функцию Ф(x), которая как видно из таблицы и наших наблюдений касательно поведения функции при росте ее аргумента, оказывается всюду определенной. Необходимо обратить особое внимание на то, что такой вывод мы может сделать только при рассмотрении конкретной заданной функции, в общем же случае, как будет показано позднее, невозможно придумать алгоритм, который на основе анализа системы рекурсивных уравнений некоторого типа сможет ответить на вопрос о принадлежности функции к классу общерекурсивных.
В данном случае вычисление значения функции Ф(х) дает следующие результаты (табл. 13.2.(2))
| x= | уравнение | f(x) | уравнение | Ф(x) |
| f(0)=3 | Ф(0)+0=3 | Ф(0)=3 | ||
| f(0+1)=f(0)+2=3+2=5 | f(1)=5 | Ф(1)+ 1=5 | Ф(1)=4 | |
| f(1+1)=f(1)+2=5+2=7 | f(2)=7 | Ф(2)+ 2=7 | Ф(2)=5 | |
| f(2+1)=f(2)+2=7+2=9 | f(3)=9 | Ф(3)+ 3=9 | Ф(3)=6 | |
| f(3+1)=f(3)+2=9+2=11 | f(4)=11 | Ф(4)+ 4=11 | Ф(4)=7 |
Очевидно, что разница между значением функции f(x) и собственно значением аргумента х с ростом аргумента только увеличивается, а значит уравнение Ф(x) +x=f(x) всегда будет иметь единственное решение. Т.о. функция Ф(х) – общерекурсивная функция.
Система уравнений может быть задана через базисные операции в виде схемы рекурсии. Например, рассмотрим систему уравнений, задающую функцию F(x):

Если раскрыть операции рекурсии и обращения функций, получим:
 |
Для х=0 значение F(x) определено и равно 0. Но для х=1 наше определение “не работает”, так как выражение F(1)=my[E(y)=1], означает:
-сначала посмотри, истинно ли Е(0) = 1;
-если нет, посмотри, истинно ли Е(1) = 1;
-если нет, посмотри, истинно ли Е(2) = 1;
-если нет, то . и т.д.
Вычисление никогда не заканчивается, потому что Е(х) всегда равна нулю, и для F(1) не будет найдено никакого значения.
Вследствие этого при рассмотрении функций, заданных системами рекурсивных уравнений, будем обычно говорить о частично-рекурсивной функции. Когда говорится о частично-рекурсивной функции F(x), то надо понимать, что может не существовать значения, определенного для некоторого (или даже любого!) значения х. Если F(x) оказывается определенной для всех значений х, то будем называть ее общерекурсивной функцией. Конечно, любая общерекурсивная функция также является частично-рекурсивной.
Виды систем эконометрических уравнений. Независимые системы. Рекурсивные системы.
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования. При использовании отдельных уравнений, регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений, называемых также структурными уравнениями. Так, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.
Приведем другой пример.
При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.
В еще большей степени возрастает потребность в использовании системы взаимосвязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам. Модель национальной экономики включает в себя систему уравнений: функции потребления, инвестиций заработной платы, а также тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная (y) рассматривается как функция одного и того же набора факторов (x) :
Набор факторов 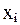
Так же является системой независимых уравнений с тем лишь отличием, что в ней набор факторов видоизменяется в уравнениях, входящих в систему. Отсутствие того или иного фактора в уравнении системы может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак (незначимо значение t- критерия или частного F-критерия для данного фактора).
Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели, характеризующие эффективность сельскохозяйственного производства, продуктивность коров, себестоимость 1 ц молока, а в качестве факторов- специализация хозяйства, количество голов на 100 га пашни, затраты труда и т.п.
Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Поскольку никогда нет уверенности, что факторы полностью объясняют зависимые переменные, то в уравнениях присутствует свободный член a0. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки.
В итоге система независимых уравнений при трех зависимых переменных и четырех факторах примет вид:
Однако если независимых переменная у донного уравнения выступает в виде фактора x в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
В данной системе зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов x. Примером такой системы может служить модель производительности труда и фондоотдачи вида:
Где y1 – производительность труда;
x1 – фондовооруженность труда;
x2 – энерговооруженность труда;
x3 – квалификация рабочих.
Как и в предыдущей системе, каждое уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях- в правую часть системы:
Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные (y) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от предыдущих систем каждое уравнение системы одновременных уравнений не может рассматриваться самостояа уравнений называется также структурной формой модетельно, и для нахождения его параметров традиционный МНК неприменим. С этой целью используются специальные приемы оценивания.
Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида.
где y1— темп изменения месячной заработной платы;
y2 – темп изменения цен;
x1— процент безработных;
x2 – темп изменения постоянного капитала;
x3 – темп изменения цен на импорт сырья.
В чем особенность рекурсивных уравнений
Система уравнений рекурсивных
Если из модели исключить тождество дохода, число предопределенных переменных модели уменьшится на 1 (из модели будет исключена переменная G,). Число эндогенных переменных модели также снизится на единицу — переменная Y, станет экзогенной. В правых частях функции потребления и функции денежного рынка будут находиться только предопределенные переменные. Функция инвестиций постулирует зависимость эндогенной переменной I, от эндогенной переменной г, (которая зависит только от предопределенных переменных) и предопределенной переменной /,.]. Таким образом, мы получим рекурсивную систему. Ее параметры можно оценивать обычным МНК, и нет необходимости исследования системы уравнения на идентификацию. [c.121]
Запишем 1-е уравнения рекурсивной системы для всех п периодов наблюдений в следующем виде [c.412]
Однако если зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений [c.179]
Как уже отмечалось, не все эконометрические модели имеют вид системы одновременных уравнений. Так, широкий класс функций спроса на ряд потребительских товаров часто представляет собой рекурсивную систему, в которой с уравнениями можно работать последовательно и проблемы одновременного оценивания не возникают. [c.212]
Система рекурсивных уравнений — система, в которой зависимая [c.31]
Среди систем одновременных уравнений наиболее простыми являются рекурсивные системы, для оценивания коэффициентов которых можно применять обыкновенный метод наименьших квадратов. [c.412]
Наиболее распространенные методы оценивания системы одновременных уравнений. Формальное применение мнк для получения оценок коэффициентов системы одновременных уравнений приводит, вообще говоря, к оценкам с плохими статистическими свойствами — смещенным и несостоятельным. Поэтому область его применения ограничена рекурсивными системами. Для оценивания параметров точно идентифицируемой системы можно применить косвенный метод наименьших квадратов, состоящий в оценивании обычным мнк коэффициентов приведенной формы и подстановке оценок в выра- [c.414]
Независимо от того, хотим ли мы оценить одно из уравнений системы или же намерены оценить каждое уравнение модели, мы оказываемся в ситуации, когда ни обыкновенный метод наименьших квадратов, ни его модификации, рассмотренные в главах о модели, состоящей из одного уравнения, в общем случае не обеспечивают удовлетворительную процедуру оценивания. Если обыкновенный метод наименьших квадратов применяется к уравнению модели, в которое обычно будут входить несколько текущих значений эндогенных переменных, то придется одну из них выбрать в качестве зависимой переменной для данного уравнения. Тогда оставшиеся (одно или несколько) текущие значения эндогенных переменных, участвующие в этом соотношении, будут, вообще говоря, коррелировать с возмущающим воздействием и поэтому оценки, найденные обыкновенным методом наименьших квадратов, окажутся смещенными и несостоятельными. Только в случае рекурсивных моделей обыкновенный метод наименьших квадратов, как мы увидим в параграфе 13.1, дает нам оптимальный способ оценивания. [c.375]
С точки зрения оценивания простейшей из всех систем одновременных уравнений является рекурсивная система. Как мы уже видели в гл. 12, она характеризуется треугольной матрицей В и диагональной матрицей S. Вернемся к рассмотрению модели [c.376]
Методы корреляций и регрессий создавались как методы описания совместных изменений двух и более переменных. Совместные изменения переменных могут не означать наличия причинных связей между ними. Потребность в причинном объяснении корреляции привела американского генетика С. Райта к созданию метода путевого анализа (1910—1920) как одного из разновидностей структурного моделирования. Путевой анализ основан на изучении всей структуры причинных связей между переменными, т. е. на построении графа связей и изоморфной ему рекурсивной системы уравнений. Его основным положением является то, что оценки стандартизированных коэффициентов рекурсивной с истемы уравнений, которые интерпретируются как коэффициенты влияния (путевые коэффициенты), рассчитываются на основе коэффициентов парной корреляции. Это позволяет проанализировать структуру корреляционной связи с точки зрения причинности. Каждый коэффициент парной корреляции рассматривается как мера полной связи двух переменных. [c.18]
Для формальной верификации гипотез необходимо соответствие между графом и системой уравнений, его описывающей. Алгебраическая система, соответствующая графу без контуров (петель), является рекурсивной системой, позволяющей рекур-рентно определять значения входящих в нее переменных. В такой системе в уравнения для признака xt включаются все переменные, за исключением расположенных выше его по графу связей. Формулировка гипотез в структуре рекуррентной модели обычно не вызывает затруднений при использовании данных в динамике. Если же анализируются статистические данные, то следует учитывать зависимость системы от ее прошлых состояний. [c.213]
Невзаимозависимые системы. Одновременные уравнения. Проблема идентификации. Точно идентифицированные и сверхидентифицированные уравнения. Косвенный метод. Двухша-говый метод наименьших квадратов. Разные формы оператора двухшагового метода. Метод наименьшего дисперсионного соглашения. Оценки k-класса. Рекурсивные системы. Трех-шаговый метод оценки параметров системы уравнения. [c.85]
СВЯЗИ В СИСТЕМЕ. Определений термина связь — десятки. Самое общее таково это то, что объединяет элементы системы в одно целое. Связи между элементами системы могут быть жесткими (таковы они обычно в технике) и гибкими, изменяющя-мися в процессе функционирования системы, — таковы они в экономике, в живых существах, в обществе. С точки зрения кибернетики связь— это процесс обмена информацией, который регулирует поведение систем (т. е. управляет ими). Наиболее важными считаются следующие виды связей обратные, рекурсивные, синерги-ческие (т. е. усиливающие) и циклические. В экономико-математической модели они выражаются через уравнения связи или неравенства связи [c.51]
В рекурсивной системе с диагональной ковариационной матрицей Е оценка FIML получается применением OLS отдельно к каждому уравнению. [c.174]
http://helpiks.org/8-13826.html
http://economy-ru.info/info/15300/