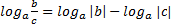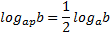В каком классе изучают логарифмические уравнения

Алгебра и начала анализа в 11-м классе по теме «Логарифмы»

Разделы: Математика

Вид урока: обобщение и систематизация.

Цели:

• создать условия для:
  • обобщения и закрепления понятия и свойств логарифма;
  • закрепления навыков чтения графика, решения логарифмических уравнений и неравенств;
• определить степень усвоения темы учащимися.

Оборудование: доска, таблицы, компьютер, проектор, экран, учебная и научная литература, справочники.

I. Организационный момент

Класс разделен на группы по 5–6 человек.

Учитель. Французский писатель Анатоль Франс (1844–1924) заметил: «Что учиться можно только весело. Чтобы переварить знания, надо поглощать их с аппетитом».
Последуем совету писателя: будем на уроке активны, внимательны, будем «поглощать» знания с большим желанием, ведь они скоро нам понадобятся для успешной сдачи экзамена.
Перед нами стоит задача: повторить логарифмическую функцию, и решение логарифмических уравнений и неравенств.

Сегодняшний урок пройдет в форме игры, математической эстафеты. Давайте познакомимся с ее условиями (слайды с правилами игры):

1. Каждая команда выбирает капитана.
2. Побеждает та команда, которая первой придет к финишу.
3. В личном первенстве победителем становится учащийся, набравший наибольшее количество очков (километров).
4. Участники игры имеют право обращаться в «консультационный пункт» – стол, на котором разложены учебная и научная литература, справочники, решения типовых заданий.
5. Эстафета состоит из четырех этапов, в ходе которых вы покажете:
а) знания свойств, определений (1 задание)
б) умения устно вычислять (2 задание)
в) умения читать график (3 задание)
г) умения решать уравнения и неравенства (4 задание)

Задание 1.

1.1. «Математические термины»

Учитель. Перед вами кроссворд, вам необходимо вписать математические термины по горизонтали. За каждый правильно вписанный термин команда получает – 1 км.

1.2. «Выбери вопрос»

Учитель. Обратите внимание на доску. Перед вами листы с номерами от 1 до 12, на обратной стороне которых написаны вопросы. Капитану команды нужно назвать номер листа, я зачитываю вопрос, и команда ответит на него. За каждый правильный ответ команда получает – 3 км, за неправильный ответ или отказ снимается – 1 км, один из участников команды может отправиться на консультационный пункт. После консультации команда снова отвечает на вопрос, в случае правильного ответа получает – 2 км.

1. Дайте определение логарифма числа по заданному основанию.
2. Запишите основное логарифмическое тождество.
3. Запишите формулу логарифм произведения.
4. Запишите формулу логарифм частного.
5. Запишите формулу логарифм степени.
6. Запишите формулу логарифмического перехода от одного основания к другому основанию.
7. Когда логарифм равен единице, нулю?
8. Какие логарифмы называются десятичными, натуральными и как они обозначаются?
9. Дайте определение логарифмической функции.
10. Какие область определения и область значения функции у = log_ax?
11. В каком случае функция у = log_ax является возрастающей, в каком убывающей?
12. При каких значениях x функции у = log_ax принимает положительные значения, при каких отрицательные?

1.3. «Графический диктант»

Учитель. Вам зачитываются утверждение, если оно верно, вы ставите знак «+», не верно – «–». Знаки ставятся в строчку через запятую. За каждый правильный ответ команда получает – 1 км.

Задание 2. Перестрелка (вычислить устно).

Командам показывается слайд № 1.

Учитель. Поднимите руку те, кто хотя бы раз играл в «Морской бой»? Ну тогда вы легко справитесь со следующим заданием. На слайде вы видите таблицу. Капитан команды называет по горизонтали число, а по вертикали букву (например, 2А). Та команда которая первая даст правильный ответ получает – 1 км и продолжает игру, а начнет ее, команда, набравшая меньшее количество очков (километров). (Учитель по ключу следит за правильностью ответов и подает сигнал к продолжению игры).

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок № 24. Логарифм. Свойства логарифмов.

Перечень вопросов, рассматриваемых в теме

1. Определение логарифма.

2. Основное логарифмическое тождество.

3. Свойства логарифмов.

Глоссарий по теме

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Логарифмирование – это действие нахождения логарифма числа.

Основное логарифмическое тождество:

Свойства логарифмов. При , справедливы равенства:

— логарифм произведения: ;

— логарифм частного: ;

— логарифм степени: .

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. – М.: Просвещение, 2014. – 384 с.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

При решении простейших показательных уравнений не всегда можно найти точный ответ. Например, уравнение имеет корень 5, т. к. значит , В уравнении число 5 не является степенью 2, значит предыдущий способ решения не подходит. Нам известно, что уравнение имеет единственный корень. Посмотрим это на графике.

Абсцисса точки пересечения – единственное решение данного уравнения. Это число и называют логарифмом 5 по основанию 2.

Дадим определение логарифма.

Логарифмом положительного числа по основанию , называется показатель степени, в которую надо возвести чтобы получить .

Т. е. логарифм числа по основанию , есть некоторое число такое, что .

, т. к. выполнены все условия определения:

1) 216 > 0; 2) 6 > 0, 6 ≠ 1; 3) .

, т. к. выполнены все условия определения:

1) ; 2) 2 > 0, 2 ≠ 1; 3) .

Это действие называется логарифмированием.

Логарифмирование – это действие нахождения логарифма числа.

Существует краткая запись определения логарифма:

так называемое основное логарифмическое тождество. Его используют при вычислениях.

(Читают: 4 в степени логарифм 5 по основанию 4 равен 5)

(Читают: одна треть в степени логарифм 6 по основанию одна треть равен 6)

Решим несколько задач с использованием определения логарифма.

Задача 1. Вычислить .

Решение. Пусть тогда по определению логарифма Приведем левую и правую части к одному основанию. 27 = 3 3 , 81 = 3 4 , значит . Отсюда следует, что

Задача 2. Вычислить .

Решение. Для вычисления воспользуемся свойствами степеней: 1) , 2) и основным логарифмическим тождеством: .

.

Для решения более сложных задач потребуется знание свойств логарифмов. Рассмотрим их.

1. Логарифм произведения.

Логарифм произведения чисел по основанию равен сумме логарифма по основанию и логарифма по основанию .

2. Логарифм частного.

Логарифм частного чисел по основанию равен разности логарифма по основанию и логарифма по основанию .

3. Логарифм степени.

Логарифм числа по основанию равен произведению показателя и логарифма по основанию .

Важно! Свойства выполняются при ,

Примеры и разбор решения заданий тренировочного модуля

№ 1. Вычислите: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

1. 
2. ;
3. .

Представим в виде степени с рациональным показателем: . Далее воспользуемся свойством нахождения логарифма степени: . Вспоминаем таблицу квадратов: , значит , . Ответ: .

Чтобы выполнить это задание нам понадобятся следующие определения и свойства:

1. ;
2. ;
3. ;
4. 
5. .
6. 

.

Изучение логарифмов в старшей школе

Понятие логарифма

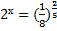
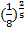
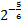
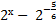
При решении показательных уравнений удается представить обе части уравнения в виде степеней с одинаковыми основаниями и рациональными показателями. Так, например, при решении уравнения мы заменяем степенью и из равенства степеней с одинаковыми основаниями делаем вывод о равенстве показателей: х = −5/6. Однако, чтобы решить, казалось бы, более простое уравнение 2 х = 3, стандартных знаний оказывается недостаточно. Дело в том, что число 3 нельзя представить в виде степени с основанием 2 и рациональным показателем.

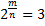
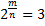
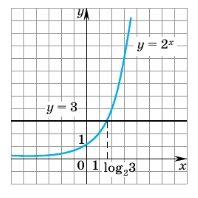
Действительно, если бы равенство , где m и n — натуральные числа, было верным, то, возведя его в степень n, мы должны были бы получить верное равенство 2 m = 3 n . Но последнее равенство неверно, так как левая его часть является четным числом, а правая — нечетным. Значит, не может быть верным и равенство .

С другой стороны, график непрерывной функции y = 2 x пересекается с прямой y = 3, и, значит, уравнение 2 x = 3 имеет корень. Таким образом, перед нами стоят два вопроса: «Как записать этот корень?» и «Как его вычислить?».

Показатель степени, в которую нужно возвести число a (a > 0, a ≠ 1), чтобы получить число b, называется логарифмом b по основанию a и обозначается log_ab.

Теперь мы можем записать корень уравнения 2 х = 3:

Равенства a x = b и x = log_ab, в которых число a положительно и не равно единице, число b положительно, а число x может быть любым, выражают одно и то же соотношение между числами a, b и x. Подставив в первое равенство выражение x из второго, получим основное логарифмическое тождество.

Понятие логарифма в методическом пособии

Задание

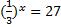
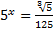
Решите уравнение: а) 2 x = 64; б) ; в) ; г) 4 x = 0; д) 7 x = −12.

После проверки ученикам предлагается ответить на вопрос, какое из заданий показалось им наиболее трудным. Вероятный ответ: 2 (в), так как в нем нужно было приводить дробь к степени числа 5. Затем школьникам предлагается высказать мнение о сравнительной с заданием 2 (в) трудности уравнения 2 x = 3. На первый взгляд кажется, что это уравнение проще, однако представить 3 в виде степени числа 2 школьникам не удается.

Дальше изучение нового материала проводится в соответствии с учебником. При этом в зависимости от уровня класса рассматривается или не рассматривается дополнительный материал о невозможности представления 3 в виде 2 r , где r = m/n.

После этого диалог с классом можно строить примерно так:

— Как вы думаете, имеет ли уравнение 2 x = 3 корень? Ответ обоснуйте. [Если построить график функции у = 2 x и провести прямую у = 3, то они пересекутся в одной точке, значит, уравнение имеет один корень.]
— Что можно сказать о корне уравнения a x = b, где а > 0 и а ≠ 1? При всех ли значениях b оно имеет корни?

Затем вводится определение логарифма числа b по основанию а и записывается основное логарифмическое тождество 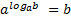. При этом выписывание равенства происходит синхронно с повторным чтением определения теперь уже в обратном, по сравнению с учебником, порядке. Теперь можно записать корень уравнения 2 х = 3: х = log_a3 и предложить школьникам серию самостоятельных работ.

Логарифмическая функция

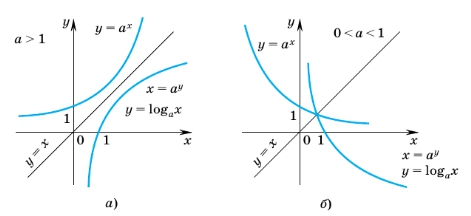
Выразим x из равенства y = log_ax, получим x = a y . Последнее равенство задает функцию x = a y , график которой симметричен графику показательной функции y = a x относительно прямой y = x.

Показательная функция x = a y является монотонной, и, значит, разные значения y соответствуют разным значениям x, но это говорит о том, что y = log_ax, в свою очередь, является функцией x.

Показательная функция y = a x и логарифмическая функция y = log_ax являются взаимно обратными. Сравнивая их графики, можно отметить некоторые основные свойства логарифмической функции.

Свойства функции y = log_ax, a > 0, a ≠ 11:

1. Функция y = log_ax определена и непрерывна на множестве положительных чисел.
2. Область значений функции y = log_ax — множество действительных чисел.
3. При 0 1 функция y = log_ax является возрастающей.
4. График функции y = log_ax проходит через точку (1; 0).
5. Ось ординат — вертикальная асимптота графика функции y = log_a.

Решение логарифмических уравнений и неравенств на основе свойств логарифмической функции

Освобождаясь от внешнего логарифма, имеющего основание 3, мы ссылаемся на возрастание соответствующей логарифмической функции, то есть на то, что большему значению логарифма соответствует большее значение выражения, стоящего под его знаком. Однако следует иметь в виду, что если функцию y = log₃ log_0,5(2x + 1) считать логарифмической, то ее аргумент не переменная x, а все выражение log_0,5(2x + 1). Если же все-таки рассматривать x как аргумент функции y = log₃ log_0,5(2x + 1), то эта функция окажется убывающей, так как при увеличении значения x увеличивается значение выражения 2x + 1, уменьшается значение выражения log_0,5(2x + 1) и, соответственно, уменьшается значение самой функции.

Свойства логарифмов

Связь двух форм записи соотношения между числами a, b и x (речь о a x = b и x = log_ab) позволяет получить свойства логарифмов, основываясь на известных свойствах степеней.

Рассмотрим, например, произведение степеней с одинаковым основанием: a x a y . Пусть a x = b и a y = c. Перейдем к логарифмической форме: x = log_ab и y = log_ac, тогда bc = a log _a b × a log _a c = a log _a b + log _a c . От показательной формы равенства bc = a log _a b + log _a c перейдем к логарифмической форме:

Заметим, что в левой части формулы числа a и b могут быть отрицательными. Тогда формула будет выглядеть так:

Аналогично можно получить еще два свойства для логарифмов частного и степени.

• логарифм произведения log_a(bc) = log_a|b| + log_a|c|
• логарифм частного
• логарифм степени log_abp= p log_a|b|

Последнее свойство дает возможность вывести важную формулу, с помощью которой можно выразить логарифм с одним основанием через логарифм с другим основанием.

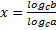
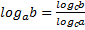
Пусть log_ab = x. Перейдем к показательной форме a x = b. Прологарифмируем это равенство по основанию c, т.е. найдем логарифмы с основанием c обеих частей этого равенства: log_ca x = log_cb. Применяя к левой части свойство логарифма степени, получим x log_ca = log_cb или , откуда .

Формула перехода от одного основания логарифма к другому

Полезно запомнить частный случай формулы перехода, когда одно из оснований является степенью другого:

Рассмотренные свойства и формула перехода «работают», конечно, только когда все входящие в них выражения имеют смысл.